Sillage d’un navire

Contenu

4.6. Sillage d’un navire#

Fig0: Sillage d'un cargo

Étudiées depuis la fin du XIXe siècle par William Froude et William Thomson (lord Kelvin), les ondes de surface de l’eau sont à l’origine des sillages issus du déplacement des bateaux, qui provoquent une résistance de vague à l’avancement.

Nous étudierons ici la forme en V de ce sillage, en utilisant la théorie de Kelvin datant de la fin du XIXe, en s’inspirant des articles de Marc Rabaud[1],[3] et de Wikipédia[2].

4.6.1. Hypothèses#

On considère un navire se déplaçant en ligne droite (suivant x) à une vitesse $U$ constante, sur une étendue d’eau initialement immobile et très profonde. On note L la longueur du bateau, qui est la principale caractéristique géométrique du problème. Les ondes de surface dépendent donc du nombre de Froude défini par:

\[Fr = \frac{U}{\sqrt{gL}}\]

On se place dans le cas linéaire de petites perturbations en eau profonde. Une onde circulaire de vecteur d’onde $\vec{k}$ (de nombre d’onde k ):

\[k=\lVert \vec{k} \rVert \mbox{ et } \vec{k} = k \vec{e_k}\]

et de pulsation $\omega$, décrivant la perturbation de la surface libre s’écrit:

\[h(\vec{r},t) = A e^{\imath(\vec{k}.\vec{r} - \omega t)} = A e^{\imath k (\vec{e_k}.\vec{r} - v_\phi t)}\]

La vitesse de phase $v_\phi = \frac{\omega}{k}$ est égale à la célérité $c$ des ondes en eau profonde. Cette célérité $c$ dépend du nombre d’onde k et est donnée par (voir cours):

(4.2)#\[v_\phi=c \mbox{ avec } v_\phi = \frac{\omega}{k} \mbox{ et } c = \sqrt{\frac{g}{k}}\]

Cette onde est dispersive avec une vitesse de groupe $v_g$ (célérité d’un paquet d’ondes) donnée par

\[ v_g = \frac{d\omega}{dk} = \frac{1}{2} v_\phi \]

Expérimentalement, on constate que vu du bateau, le sillage est stationnaire, i.e. fixe par rapport au bateau et à la forme caractéristique de la figure ci-dessous.

../_images/sillagePhoto.jpeg — Fig. 4.28 Sillage stationnaire d’un bateau (C) Wikipedia [2]#

Les hypothèses du modèle sont donc

analyse linéaire (petites perturbations)
ondes de surface dispersives en eau profonde: $v_g = \frac{1}{2} v_\phi$
sillage fixe (stationnaire) par rapport au bateau

4.6.2. Sillage de Kelvin#

On veut déterminer quelles sont les ondes de surface émises par le déplacement du bateau qui contribuent à la formation du sillage.

Pour cela on étudie le sillage du navire à l’instant $t=0$ et à la position $N$. Ce sillage est constitué d’ondes émises par le navire à des instants précédents. Soit $O$ la position du navire à un instant $t=-\tau$, t.q.
$ON= U\tau$.

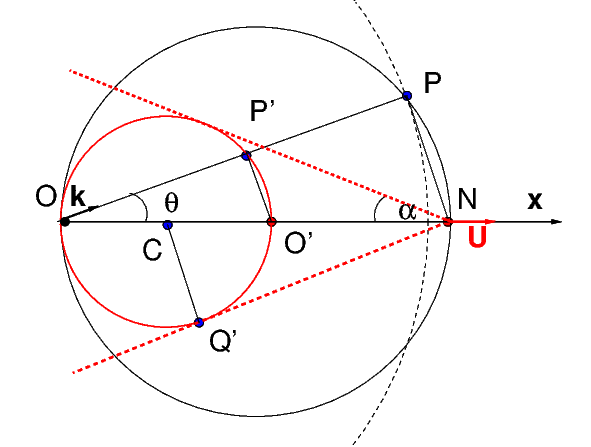
../_images/sillage.png — Fig. 4.29 schéma de propagation d’ondes issues de $O$ dans le sillage d’un bateau en $N$#

A cet instant le navire a émis en $O$ une onde circulaire de vecteur d’onde $\vec{k}$ et de pulsation $\omega$. A l’instant étudié $t=0$, cette onde s’est propagée jusqu’à un cercle de centre $O$ et de rayon $r=\lVert \vec{OP}\rVert=c\tau$. Dans le référentiel fixe, la phase $\Phi$ de cette onde $Ae^{\imath\Phi}$ qui s’est propagée jusqu’en $P$, s’écrit sous la forme:

\[\Phi = (\vec{k}.\vec{r} - \omega \tau)\]

En écrivant la position $P$ par rapport au navire en $N$ et en notant $r'=\lVert \overrightarrow{NP}\rVert$

\[\overrightarrow{OP} = \overrightarrow{ON} + \overrightarrow{NP}\]

on en déduit la phase vue du navire:

\[\Phi = (\vec{k}.\vec{r'} +(\vec{k}.\vec{U}- \omega) \tau)\]

Vue du navire, le sillage est fixe. Cette phase doit donc être indépendante de $\tau$ pour que l’onde, ne dépendant que de $\vec{r'}$, soit fixe par rapport au bateau, d’où:

\[ \omega = \vec{k}.\vec{U} \]

ce qui impose:

\[ \lVert\overrightarrow{OP}\rVert = \lVert\overrightarrow{ON}\rVert \cos\theta \mbox{ soit } v_\phi = U \cos\theta \]

et qui sélectionne une seule direction d’onde d’angle $\theta$ pour chaque nombre d’onde $k$ et pulsation $\omega$. Sur la figure, cela correspond au point $P$ tq $\lVert\overrightarrow{OP}\rVert$ soit perpendiculaire à $\lVert\overrightarrow{NP}\rVert$. En notant $(x,y)$ les coordonnées de P par rapport au milieu $O'$ de $ON$, on montre facilement que la condition d’orthogonalité impose que $(x^2-R^2)+y^2=0$ où $R$ est la motié de la distance $ON$, donc $P est sur le cercle $C_0$ de diamètre $ON$. $P$ est donc à l'intersection du cercle de centre $O$ et de rayon $\lVert\overrightarrow{OP}\rVert=v_\phi \tau$ et du cercle $C_0$ de diamètre $\lVert\overrightarrow{ON}\rVert=U\tau$ centré en $O”$ milieu de $O$ et $N$.

Si on fait varier la vitesse de phase $v_\phi$ en faisant varier k et $\omega$ (tout en vérifiant l’équation (4.2)), on considère alors une onde circulaire de vitesse $v'_\phi$ émise en $O$ à $t=-\tau$ et qui à $t=0$ se trouve sur un cercle de rayon $v'_\phi\tau \neq v_\phi\tau$. La seule direction de cette onde qui participe au sillage correspond à la direction $\theta'$ t.q. $v'_\phi = U \cos \theta'$ et le point $P'$ correspondant se trouve aussi sur le cercle $C_0$.

Réciproquement, pour tout point du cercle $C_0$, on peut trouver une vitesse de phase $v_{\phi}$ et une onde associée (caractérisée par $k$ , $\omega$ et $\theta$) issue de $O$ qui participe au sillage du bateau.

Cependant le raisonnement doit être adapté au fait que la vitesse de phase $v_\phi$ des ondes, i.e. la vitesse à laquelle avance la crête des ondes, est différente de la vitesse de groupe $v_g$, i.e. la vitesse à laquelle l’énergie de ces ondes est transportée et c’est cette vitesse de groupe qu’il faut prendre en compte pour la caractérisation du sillage, puisque le bateau génère un paquet d’onde (et non une onde simple).

Pour $\omega$, $k$ et $\tau$ donnés, on a vu qu’on déduisait la position du point $P$ où, à l’instant zéro, l’onde possède la même phase qu’en $O$ à l’instant $-\tau$ où elle est née. Pour cette onde, le pic d’énergie n’est pas en $P$ mais a voyagé deux fois plus lentement, à la vitesse de groupe. Donc ce pic, à l’instant zéro, se situe au point $P'$, à mi-chemin entre $O$ et $P$. Par une homothétie de centre $O$ et de rapport 1/2, on en déduit que $P'$ se trouve sur le cercle $C_1$ de diamètre $OO'$ ($O'$ milieu de $ON$). C’est donc en $P'$ que l’onde créée en $O$ à l’instant $-\tau$ participe au sillage à l’instant zéro.

4.6.3. Cône de sillage#

Pour tout point du cercle $C_1$, on peut trouver une onde associée issue de O (à l’instant $-\tau$) qui participe au sillage du bateau. En diminuant la valeur de $\tau$ jusqu’à zéro, on définie des séries de cercles $C_1$ de plus en petits et se rapprochant de $N$ et on reconstitue le sillage stationnaire du bateau. Ce sillage est délimité par les 2 droites issues de $N$ et tangentes à ces cercles. Soit $\alpha$ le demi-angle aux sommets du cône de sillage, et en notant $Q'$ le point tangent au cercle et à la droite, on a:

\[ \lVert\overrightarrow{O'N}\rVert \sin\alpha = \lVert\overrightarrow{O'Q'}\rVert \mbox{ soit } \frac{3}{4} U \tau \sin\alpha = \frac{1}{4} U\tau\]

soit

\[\sin\alpha = \frac{1}{3} \leadsto \alpha = 19.5°\]

On obtient donc un angle de sillage indépendant de la forme et de la longueur du bateau et de sa vitesse.

4.6.4. Ondes dans le sillage#

Dans le sillage, on observe 2 types d’ondes: les ondes transverses et les ondes divergentes (figure ci-dessous).

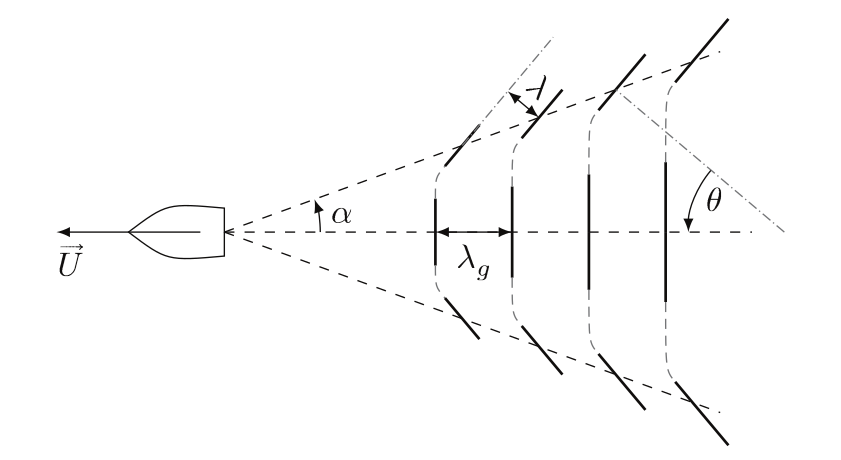
../_images/sillage1.png — Fig. 4.30 les 2 types d’ondes (transverses et divergentes) dans le sillage [3]#

Soit $\lambda_g$ la longueur d’onde des ondes transverses observées dans l’axe du bateau. Ces ondes se propagent à la vitesse de groupe $v_g=\frac{v_\phi}{2}$ associée à une vitesse de phase $v_\phi=U$ (puisque $\theta=0$). Puisque $v_\phi = \sqrt{g/k}$, on en déduit le nombre d’onde $k_g = g/U^2$ et la longueur d’onde $\lambda_g=2\pi/k_g$ :

\[\lambda_g = \frac{2\pi U^2}{g}\]

De même les ondes divergentes se propageant à la limite du sillage avec une vitesse de phase $v_\phi = U\cos\theta'$, et une longueur d’onde

\[\lambda = \frac{2\pi U^2 \cos^2\theta'}{g}\]

en notant $\theta'$ l’angle de ces ondes. On a donc la relation suivante entre les longueurs d’ondes:

\[\cos\theta' = \sqrt{\frac{\lambda}{\lambda_g}} \]

En notant que

\[ \lVert\overrightarrow{OQ'}\rVert \sin\theta' = \lVert\overrightarrow{NQ'}\rVert \sin\alpha\]

on montre aussi que

\[\frac{1}{2} \sin 2\theta' = \frac{3}{4} \sin 2\alpha\]

En élevent cette relation au carré, et en l’exprimant en fonction de $\cos^2\theta'$ et $\sin^2\alpha$, on obtient:

\[ (1-\cos^2\theta')\cos^2\theta' = \frac{9}{4} \sin^2\alpha (1-\sin^2\alpha) \]

d’où le rapport des longueurs d’ondes:

\[\frac{\lambda}{\lambda_g}=\frac{2}{3}\]

Pour $\alpha \approx 19,5°$, on trouve $\theta' \approx 35.3°$ et $\lambda =\frac{2}{3} \lambda_g \approx 0.67 \lambda_g$

La théorie de Kelvin s’applique pour des nombres de Froude $Fr<1$ (i.e. pour des vitesses de bateaux modérées). L’observation du sillage des bateaux rapides montre que le sillage en V devient plus étroit et que son angle est alors inversement proportionnel à la vitesse [3].

4.6.5. Simulation numérique#

On peut simuler numériquement ce modèle de sillage, en sommant toutes les ondes circulaires générées par le bateau

Pour cela, on calcule toutes les ondes émises par le bateau à des instants précédents, i.e. lorsque le bateau se trouvait en $x_0$

En tout point $(x,y)$ à l’arrière du navire, on calcule la distance $r_0$ au point d’émission $x_0$:

\[ r_0 = \sqrt{(x-x_0)^2 + y^2} \]

et la somme $S_0(x,y)$ des ondes cylindriques émises en $x_0$ à $t_0= -x_0/U$. Ces ondes ont atteins le point $(x,y)$ si $r_0 \le v_\Phi t_0$ .

(4.3)#\[\begin{eqnarray} S_0(x,y) &=& \sum_{k} \cos{(k r_0 + \omega \frac{x_0}{U})} \mbox{ si } r_0 \le v_\Phi t_0 \\ S_0(x,y) &=& 0 \mbox{ sinon } \end{eqnarray}\]

Le résultat est tracé sur la figure suivante.

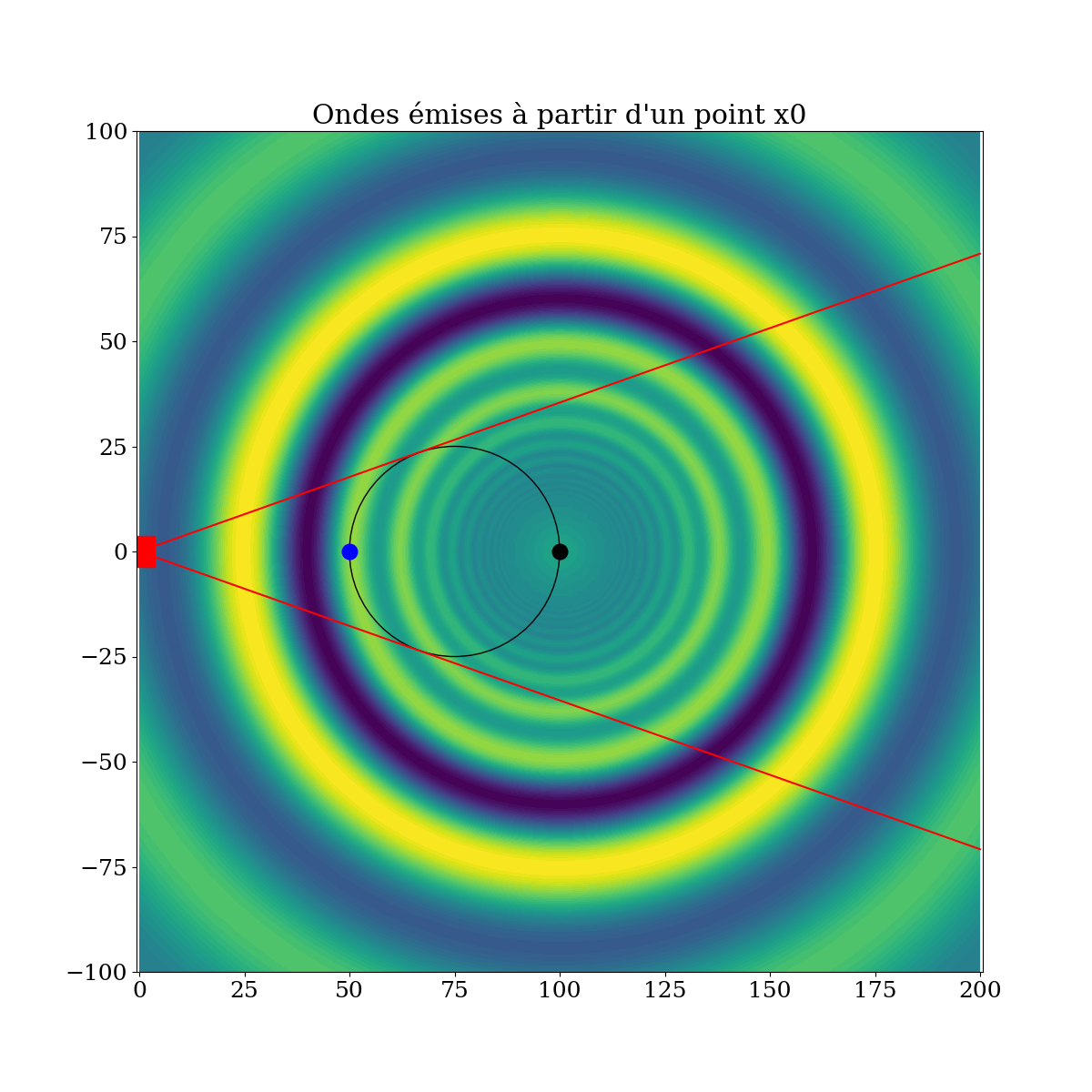
../_images/OndeSillage1.png — Fig. 4.31 Ondes émises à partir d’un point $x_0$ à un instant $t_0=x_0/U$#

En tous les points $(x,y)$ à l’arrière du navire, on calcule ensuite la somme $S(x,y)$ des contributions des points $x_0$ entre $x_0=0$ et $x_0=L$, i.e. les ondes émises entre $t=0$ et $t=-L/U$.

\[ S(x,y) = \sum_{x_0} S_0(x,y) \]

En sommant toutes les ondes émises à partir de tous les points $x_0$ à l’arrière du navire, on obtiens le sillage de Kelvin suivant avec un angle $\alpha=19,5°$. Le résultat est tracé sur la figure suivante, et on retrouve bien la forme du sillage de Kelvin.

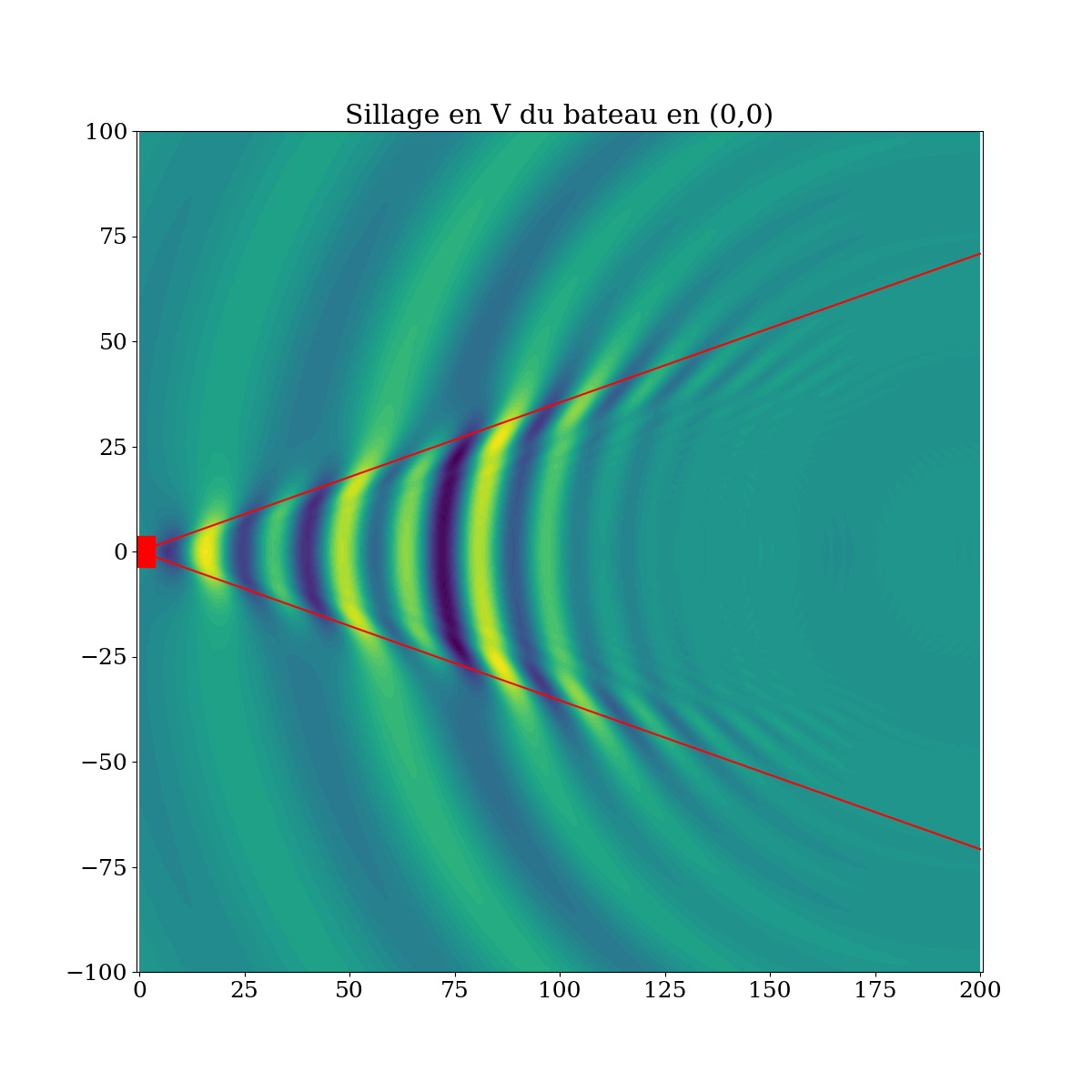
../_images/OndeSillage2.png — Fig. 4.32 Sillage calculé du bateau (carré rouge) et limite théorique de Kelvin (droite d’angle $\alpha$)#

L’amplitude des ondes dans l’axe du sillage est donnée sur la courbe suivante, et on observe bien une longueur d’onde $\lambda_g$ donnée par la relation théorique précécente.

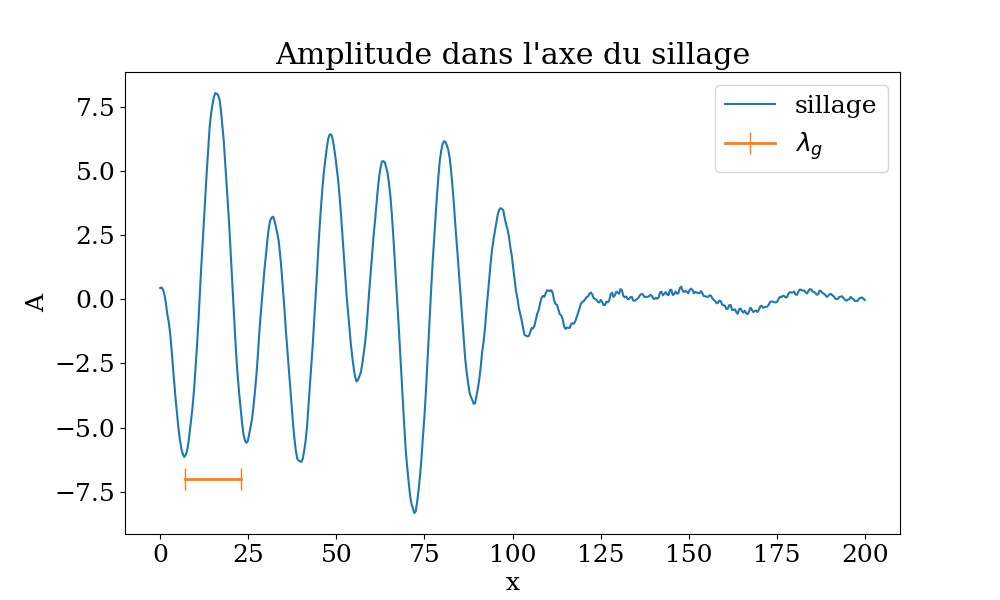
../_images/OndeSillage3.png — Fig. 4.33 Amplitude dans l’axe du sillage et comparaison avec la longueur d’onde théorique $\lambda_g$#