3. Ondes de Choc

Fig. 3.3 choc fort autour de 2 sphères

3.1. Introduction

Nous avons vu dans les chapitres précédents que dans les écoulements compressibles peuvent apparaître des zones de discontinuité, par suite par exemple de concentration d’ondes se propageant à des vitesses différentes (caractéristiques). Les équations d’Euler permettent de décrire ces discontinuités (ou chocs).

Fig. 3.4 ondes de choc sur une sphère

Dans la réalité, ces chocs apparaissent comme une très fine région de l’espace où l’on observe de très forte variation des propriétés thermodynamiques \(T,\rho,p\) et de la vitesse \(U\) du fluide. L’épaisseur d’un choc permet cependant de continuer à utiliser l’hypothèse de milieu continu.

Nous les modéliserons cependant comme des discontinuités mathématiques.

Dans un choc, il n’y a pas de création ni destruction de masse: donc l’équation de bilan de masse s’applique à travers le choc. De même, il n’y a pas de force extérieure qui s’applique dans un choc, donc on peut appliquer la bilan de quantité de mouvement. Finalement, il n’y a pas d’apport de chaleur extérieur, donc un choc est adiabatique (mais pas isentropique !).

A travers un choc, la température est discontinue. Donc un choc est une région où on transforme une partie de l’énergie cinétique (vitesse moyenne organisée des particules) en énergie interne (fluctuations internes désorganisées des particules: chaleur ou température). Et ceci ne peut se faire que dans un sens d’après le second principe: du mouvement organisé vers un mouvement désordonné. A travers un choc, l’écoulement est adiabatique, mais son entropie augmente: \(dS>0\).

3.2. Relations à travers un choc droit

Pour cela on considère un choc droit immobile à travers lequel l’écoulement reste quasi-unidimensionnel et stationnaire. Si le choc se déplace, on fait l’analyse dans un repère lié au choc.

On note \(u_{1}\), \(c_{1}\), \(p_{1},\rho_{1}\) l’état du fluide avant le choc et \(u_{2}\), \(c_{2}\), \(p_{2},\rho_{2}\) l’état du fluide après le choc.

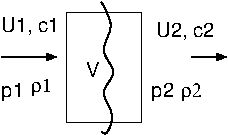
Fig. 3.5 choc droit

On fait des bilans (de masse, de quantité de mouvement et d’énergie) en considérant un petit élément de volume \(V\) incluant le choc. Ces équations s’écrivent:

1. bilan de masse:

   (3.4)\[\rho_{1}u_{1}=\rho_{2}u_{2}\]

2. bilan de quantité de mouvement:

   (3.5)\[\rho_{1}u_{1}^{2}+p_{1}=\rho_{2}u_{2}^{2}+p_{2}\]

3. conservation de l’enthalpie totale:

   \[h_{t}=\frac{1}{2}u_{1}^{2}+h_{1}=\frac{1}{2}u_{2}^{2}+h_{2}\]

En exprimant l’enthalpie \(h=C_{p}T\) en fonction de la célérité du son \(c=\sqrt{\gamma RT}\):

\[h=C_{p}T=\frac{C_{p}}{\gamma R}c^{2}=\frac{c^{2}}{\gamma-1}\]

la dernière équation s’écrit:

(3.6)\[\frac{1}{2}u_{1}^{2}+\frac{c_{1}^{2}}{\gamma-1}=\frac{1}{2}u_{2}^{2}+\frac{c_{2}^{2}}{\gamma-1}=h_{t}\]

Ce système d’équations est connue sous le nom de relations de Rankine-Hugoniot. Nous allons calculer les variations des quantités à travers le choc en fonction du nombre de Mach amont \(M_{1}=\frac{u_{1}}{c_{1}}\)

En divisant par \(\rho_{1}u_{1}=\rho_{2}u_{2}\) l’équation (3.5), il vient:

\[u_{2}-u_{1}=\frac{p_{1}}{\rho_{1}u_{1}}-\frac{p_{2}}{\rho_{2}u_{2}}\]

et en introduisant la célérité du son \(c^{2}=\frac{\gamma\,p}{\rho}\), il vient:

\[u_{2}-u_{1}=\frac{c_{1}^{2}}{\gamma u_{1}}-\frac{c_{2}^{2}}{\gamma u_{2}}\]

En utilisant l’équation (3.6), on calcule:

\[\frac{c^{2}}{\gamma u}=\frac{\gamma-1}{\gamma u}(h_{t}-\frac{1}{2}u^{2})\]

et on remplace:

\[u_{2}-u_{1}=\frac{\gamma-1}{\gamma}\left(\frac{h_{t}(u_{2}-u_{1})}{u_{1}u_{2}}+\frac{1}{2}(u_{2}-u_{1})\right)\]

Or on a supposé qu’il y avait un choc et donc une discontinuité sur la vitesse: i.e. \(u_{2}-u_{1}\neq 0\)

En simplifiant par \(u_{2}-u_{1}\), il vient:

\[\frac{\gamma}{\gamma-1}=\frac{h_{t}}{u_{1}u_{2}}+\frac{1}{2}\]

soit:

\[u_{1}u_{2}=h_{t}\frac{2(\gamma-1)}{\gamma+1}\]

ce qui nous permet de calculer le rapport

\[\frac{u_{2}}{u_{1}}=\frac{u_{1}u_{2}}{u_{1}^{2}}=\frac{h_{t}}{u_{1}^{2}}\frac{2(\gamma-1)}{\gamma+1}\]

Et d’après (3.6), on a

\[\frac{h_{t}}{u_{1}^{2}}=\frac{1}{2}+\frac{M_{1}^{-2}}{\gamma-1}\]

d’où l’expression de la variation de la vitesse à travers le choc:

(3.7)\[\frac{u_{2}}{u_{1}}=\frac{2(\gamma-1)}{\gamma+1}\left(\frac{1}{2}+\frac{M_{1}^{-2}}{\gamma-1}\right)=\frac{(\gamma-1)M_{1}^{2}+2}{(\gamma+1)M_{1}^{2}}\]

On en déduit la variation de la masse volumique

(3.8)\[\frac{\rho_{2}}{\rho_{1}}=\frac{u_{1}}{u_{2}}=\frac{(\gamma+1)M_{1}^{2}}{(\gamma-1)M_{1}^{2}+2}\]

La relation (3.6) permet de calculer la variation de célérité du son

\[c_{2}^{2}-c_{1}^{2}=\frac{(\gamma-1)}{2}(u_{1}^{2}-u_{2}^{2})\]

et en divisant par \(u_{2}^{2}\), on obtient la variation du Mach

\[M_{2}^{-2}=M_{1}^{-2}\left(\frac{u_{1}}{u_{2}}\right)^{2}+\frac{\gamma-1}{2}(\left(\frac{u_{1}}{u_{2}}\right)^{2}-1)\]

soit

(3.9)\[\left(\frac{M_{1}}{M_{2}}\right)^{2}=\left(\frac{u_{1}}{u_{2}}\right)^{2}+\frac{\gamma-1}{2}M_{1}^{2}(\left(\frac{u_{1}}{u_{2}}\right)^{2}-1)\]

Pour la pression, on utilise l’équation (3.5)

\[p_{2}-p_{1}=\rho_{1}u_{1}(u_{1}-u_{2})\]

d’où

\[\frac{p_{2}}{p_{1}}-1=\frac{\rho_{1}u_{1}^{2}}{p_{1}}(1-\frac{u_{2}}{u_{1}})=\frac{\gamma u_{1}^{2}}{c_{1}^{2}}(1-\frac{u_{2}}{u_{1}})\]

ce qui donne en remplaçant \(\frac{u_{2}}{u_{1}}\)

(3.10)\[\frac{p_{2}}{p_{1}}=1+\frac{2\gamma}{\gamma+1}(M_{1}^{2}-1)\]

Enfin en utilisant la définition de l’entropie (pour un gaz parfait):

\[S=C_{v}\ln\frac{p}{\rho^{\gamma}}\]

on obtient l’évolution de l’entropie à travers le choc:

(3.11)\[\begin{split}\begin{aligned} \frac{S_{2}-S_{1}}{C_{v}} & = & \ln\frac{p_{2}}{p_{1}}-\gamma\ln\frac{\rho_{2}}{\rho_{1}}\\ & = & \ln\left(1+\frac{2\gamma}{\gamma+1}(M_{1}^{2}-1)\right)-\gamma\ln\left(\frac{(\gamma+1)M_{1}^{2}}{(\gamma-1)M_{1}^{2}+2}\right)\end{aligned}\end{split}\]

On a tracé sur la figure ci-dessous l’évolution du saut d’entropie (3.11) en fonction du Mach amont \(M_{1}\) ainsi que le rapport le Mach \(M_{2}\) (relation sqrt((3.9))*M1)

Fig. 3.6 saut d’entropie à travers un choc droit

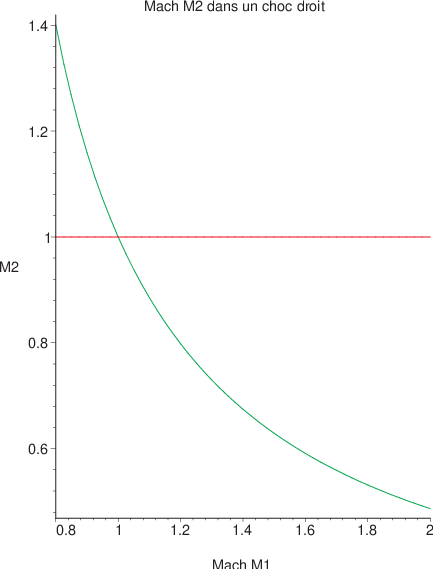
Fig. 3.7 Mach M2 pour un choc droit

De cette analyse on déduit que:

1. Si l’écoulement amont est subsonique \(M_{1}<1\), alors il ne peut pas y avoir de choc droit stationnaire car l’entropie diminue \(S_{2}<S_{1}\)

2. Si l’écoulement amont est sonique \(M_{1}=1\), il n’y a pas de choc \(M_{2}=1,\,p_{2}=p_{1},\,u_{2}=u_{1},\,\rho_{1}=\rho_{2}\)

3. si l’écoulement amont est supersonique \(M_{1}>1\), alors il y peut y avoir un choc droit stationnaire, pour lequel l’entropie augmente (écoulement irréversible) et l’écoulement aval est subsonique \(M_{2}<1\).

Nous avons tracé sur la figure ci-dessous l’évolution de la masse volumique, de la pression et de la vitesse à travers un choc droit:

Fig. 3.8 évolution de la masse volumique, pression et température pour un choc droit

Comme nous l’avons vu précédemment, un choc droit permet de décélérer l’écoulement: \(\textrm{u}_{2}<u_{1}\), à travers une compression forte adiabatique \(p_{2}>p_{1}\) et \(\rho_{2}>\rho_{1}\). L’énergie cinétique de l’écoulement est transformée en énergie interne par augmentation de l’agitation moléculaire: la température augmente à travers un choc \(T_{2}>T_{1}\).

On constate aussi que plus le Mach amont est fort, plus le choc est fort, mais il y a une limite : le Mach aval ne peut descendre en dessous d’une valeur limite \(M_{\infty}=\frac{1}{2}\sqrt{\frac{\gamma-1}{\gamma}}\simeq0.26\), ainsi que le saut de vitesse : \(\frac{u_{2}}{u_{1}}\Longrightarrow\frac{\gamma-1}{\gamma+1}=\frac{1}{6}\) , et le saut de masse volumique \(\frac{\rho_{2}}{\rho_{1}}\Longrightarrow\frac{\gamma+1}{\gamma-1}=6\). Par contre le saut de pression n’est pas borné et tend vers l’infini.

3.3. Choc instationnaire

L’analyse précédente peut se généraliser au cas d’un choc droit se déplaçant avec une vitesse constante \(V\) dans un milieu au repos. A l’amont du choc la vitesse est nulle, le fluide au repos, la masse volumique vaut \(\rho_{0}\) et la pression \(p_{0}\), et à l’arrière du choc la vitesse vaut \(U_{1}\) , la masse volumique \(\rho_{1}\), et la pression \(p_{1}\).

Pour se ramener au cas du choc droit stationnaire, on considère un repère lié au choc. Dans ce repère l’écoulement amont est donné par:

\[V,\,c_{0}=\sqrt{\gamma\frac{p_{0}}{\rho_{0}}}\]

et l’écoulement aval par:

\[V-U_{1},\,c_{1}=\sqrt{\gamma\frac{p_{1}}{\rho_{1}}}\]

Les relations (3.8), (3.9), (3.11) sont toujours valables, mais en remplaçant :

\[M_{1}=\frac{V}{c_{0}},\,\,u_{1}=V,\,\,u_{2}=V-U_{1}\]

3.3.1. Tube à choc

On considère un tube de longueur \(L\), séparé en son milieu par une membrane avec d’un coté un gaz à haute pression (\(p_{0},\rho_{0}\)) et de l’autre un gaz à basse pression (\(p_{1},\rho_{1}\)).

Fig. 3.9 tube à choc

On enlève la membrane à l’instant \(t=0\). On introduit donc une discontinuité de pression, masse volumique et température dans le tube.

Due à la différence de pression, le gaz de la chambre haute pression va se déplacer dans la chambre basse pression. Une zone entre les 2 gaz se met en mouvement avec une vitesse \(u_{3}>0\) et une pression \(p_{3}\): \(p_{1}>p_{3}>p_{2}\) avec en amont la propagation d’une onde de choc avec une célérité \(u+c=\frac{1}{2}(u_{3}+c_{3}+c_{2})\). En arrière de cette zone se développe des ondes de détente de pente \(u-c\): \(-c_{1}<u-c<u_{3}-c_{3}\). Enfin, si on néglige la diffusion, les deux gaz ne se mélangent pas, et la séparation entre les deux correspond à une discontinuité de contact qui se propage avec la vitesse \(u=u_{3}\).

On a donc le développement de 3 ondes dans le système:

1. une onde de choc de célérité \(u+c\)

2. des ondes de détente de célérité \(u-c\)

3. une discontinuité de contact de célérité \(u\)

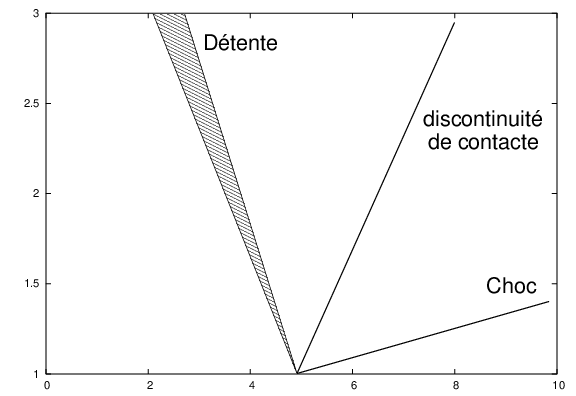
Fig. 3.10 ondes dans un tube à choc

La solution des équations d’Euler pour ce problème est donnée sur les figures suivantes à l’instant \(t=\frac{L}{4c_{1}}\), pour un rapport de pression et de masse volumique de \(3\).

Sur l’animation suivante, on a tracé l’évolution de la trajectoire des particules fluides dans un tube à choc, ainsi que l’évolution de la pression, de la vitesse, de la masse volumique et du nombre de Mach dans le tube en fonction du temps.

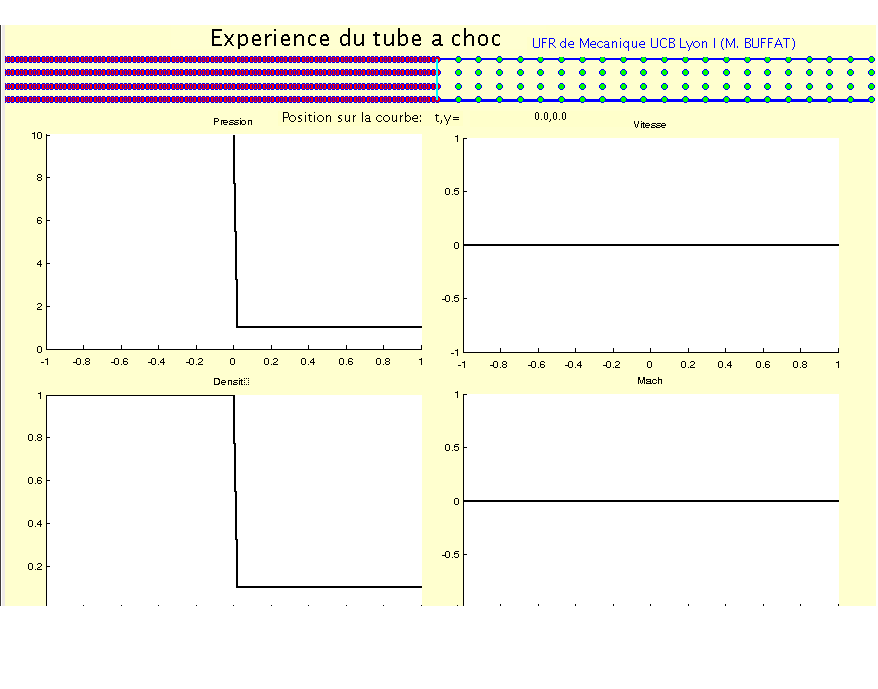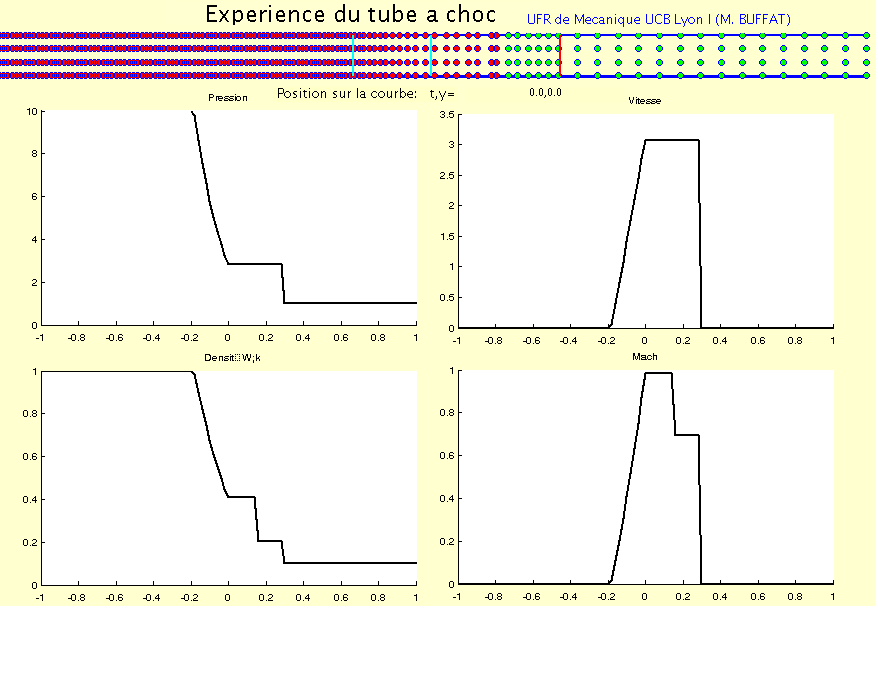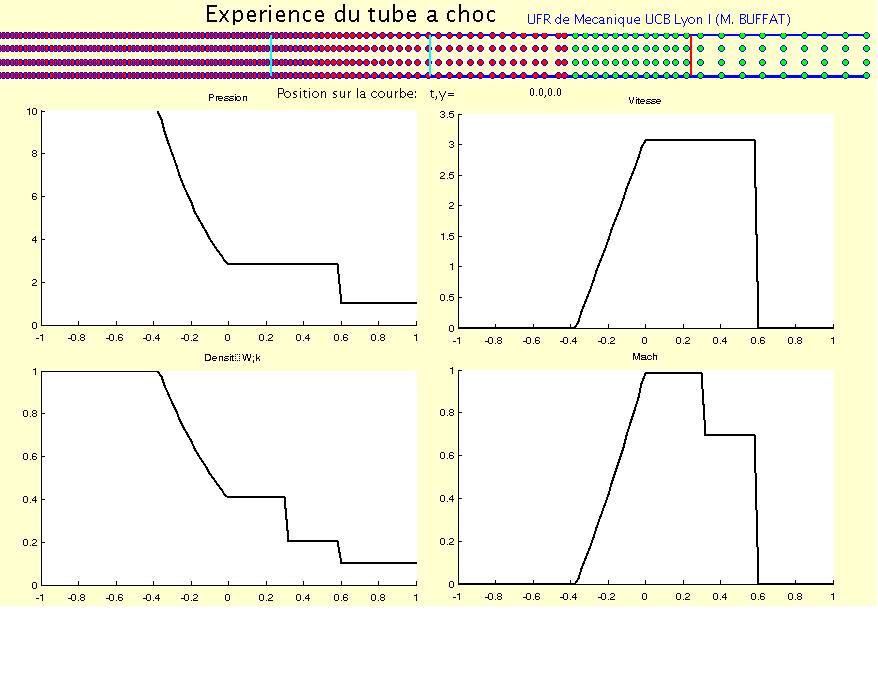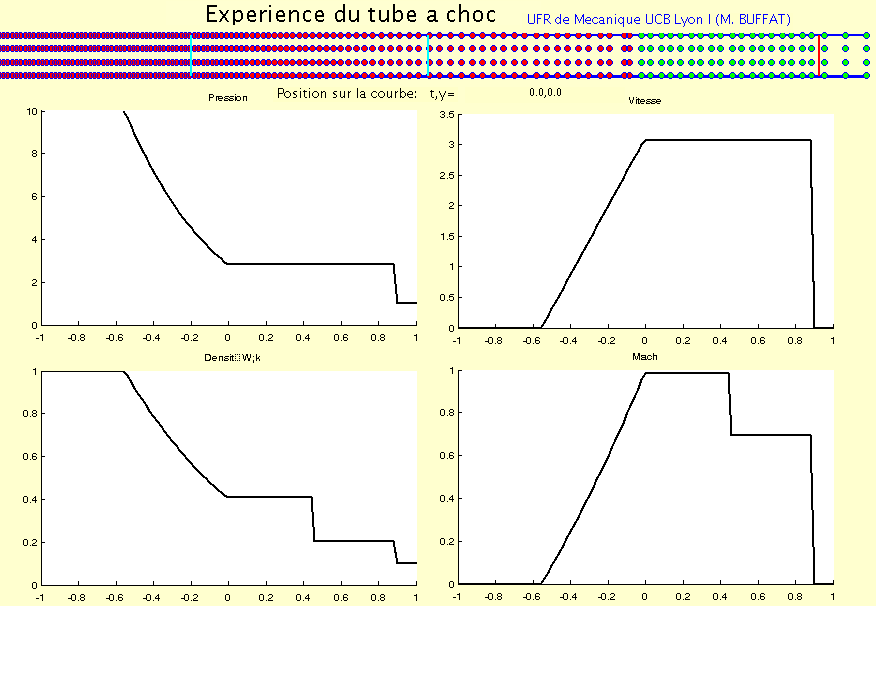
Fig. 3.11 animation tube à choc

3.3.2. Vitesse du choc crée par un piston

Dans l’expérience décrite au chapitre 3, on a créé un choc par déplacement d’un piston.

En utilisant les relations caractéristiques, dans la région entre le piston (qui génère le choc) et le choc (i.e. à l’arrière du choc), la célérité du son \(c_{1}\) vérifie:

\[c_{1}=\frac{1}{2}(\gamma-1)U_{1}+c_{0}\]

(puisque \(c_{0}\) est la célérité dans le fluide au repos)

En utilisant cette relation dans l’équation de conservation de l’enthalpie totale à travers le choc (3.6):

\[\left(\frac{1}{2}(\gamma-1)U_{1}+c_{0}\right)^{2}+\frac{\gamma-1}{2}(V-U_{1})^{2}=c_{0}^{2}+\frac{\gamma-1}{2}V^{2}\]

on en déduit la vitesse du choc

\[V=c_{0}+\frac{\gamma+1}{4}U_{1}\]

On note donc que par rapport au choc, l’écoulement amont est supersonique \(V>c_{0}\) et l’écoulement aval est subsonique \(V-U_{1}=c_{0}-\frac{3-\gamma}{4}U_{1}<c_{1}=c_{0}+\frac{\gamma-1}{2}U_{1}\).

On note aussi que la vitesse du choc \(V\) est la moyenne de la vitesse de propagation à l’amont et à l’aval du choc:

\[V=\frac{1}{2}\left(c_{0}+(c_{1}+U_{1})\right)=c_{0}+\frac{\gamma+1}{4}U_{1}\]

Sur l’animation suivante, on a tracé l’évolution de la trajectoire des particules fluides dans le piston.

Fig. 3.12 animation piston

3.4. Chocs en tuyère

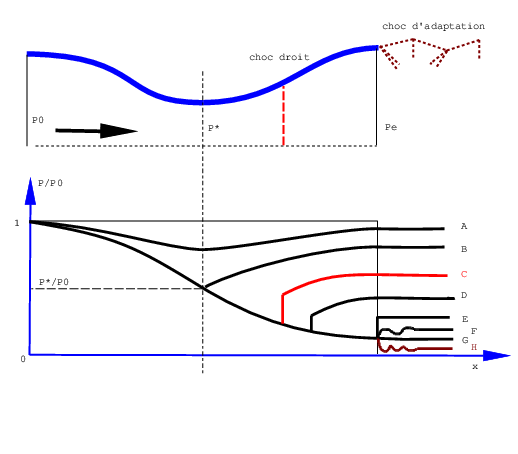
Fig. 3.13 choc dans un tuyère de Laval

Reprenons l’étude de l’écoulement dans une tuyère de Laval. Nous avons montré que l’écoulement dans la tuyère (et en particulier dans le divergent) dépendait du niveau de pression \(p_{e}\) en sortie.

1. \(p_{e}=p_{A}\) : la pression en sortie est assez haute, l’écoulement dans la tuyère est subsonique et isentropique. Les relations isentropiques (chapitre 3) donnent la répartition de pression.

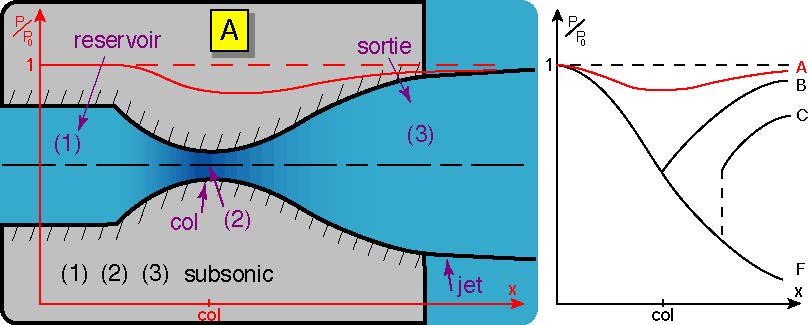
Fig. 3.14 écoulement en tuyère \(p_{e}=p_{A}\)

2. \(p_{e}=p_{B}\) : en diminuant la pression en sortie, on atteint un niveau \(p_{B}\) où l’écoulement est sonique au col, mais reste subsonique dans le divergent. L’écoulement est isentropique. Les relations isentropiques pour une tuyère adaptée donne la répartition de pression.

Fig. 3.15 écoulement en tuyère \(p_{e}=p_{B}\)

3. \(p_{e}=p_{G}\): pour un autre niveau de pression plus bas, on a encore un écoulement isentropique, avec un col sonique. Mais dans ce cas l’écoulement est supersonique dans le divergent. Les relations isentropiques pour une tuyère adaptée donne la encore la répartition de pression.

Fig. 3.16 écoulement en tuyère \(p_{e}=p_{G)\)

Pour tous les autres niveaux de pression l’écoulement n’est plus isentropique, et des chocs d’adaptation sont nécessaire.

1. \(p_{B}>p_{e}=p_{C}>p_{E}\): l’écoulement ne peut plus rester isentropique dans le divergent. Un choc droit apparaît pour passer d’un écoulement supersonique au début du divergent à un écoulement subsonique après le choc. Lorsque l’on diminue la pression \(p_{e}\) le choc se déplace vers la sortie de tuyère pour se situé exactement en sortie dans le cas \(p_{e}=p_{E}\)

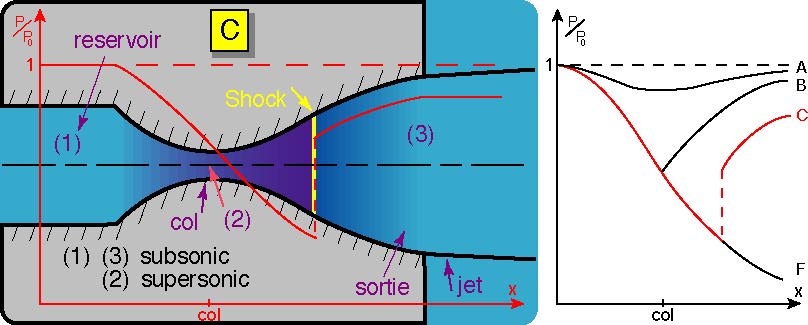
Fig. 3.17 écoulement en tuyère \(p_{e}=p_{E)\)

2. \(p_{E}>p_{e}=p_{F}>p_{G}\): le choc d’adaptation n’a plus lieu dans la tuyère, mais dans le jet au travers d’une série d’ondes de choc oblique, permettant l’adaptation de la pression. On observe en sortie un jet supersonique sur-détendu1 (over-expanded) avec apparitions de disques de Mach

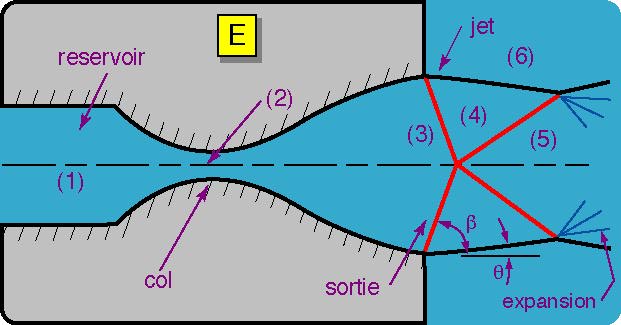
Fig. 3.18 écoulement en tuyère \(p_{e}=p_{F)\)

3. \(pe=p_{H}<p_{G}\): on a cette fois un jet supersonique sous-détendu1 (under-expanded) (i.e. qui sort de la tuyère avec une pression inférieure à la pression ambiante) avec une série d’ondes de détentes pour adapter la pression.

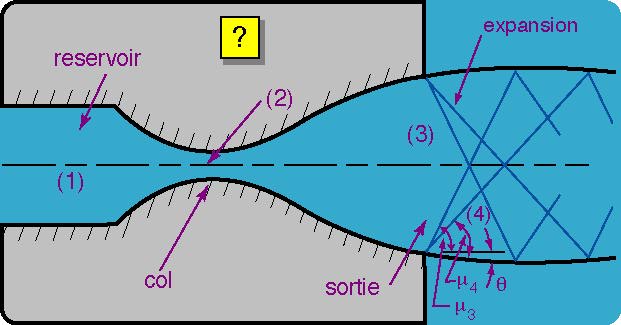
Fig. 3.19 écoulement en tuyère \(p_{e}=p_{H)\)

Un excellent site sur le design d’une tuyère de Laval pour un moteur de fusée:

• Virginia Tech. University

Fig. 3.20 écoulement dans le jet d’une tuyère

3.5. Chocs obliques

Un choc oblique est créé lorsqu’un écoulement supersonique est défléchi (par un obstacle). Un écoulement supersonique de vitesse \(U_{1}\) est défléchi par une rampe d’angle \(\theta\). Un choc oblique d’angle \(\beta\) apparaît pour permettre à l’écoulement d’avoir une vitesse \(U_{2}\) parallèle à la rampe.

La géométrie du choc oblique est donnée sur la figure ci-dessous

Fig. 3.21 choc oblique

On décompose la vitesse \(U\) suivant la direction normale au choc \(U_{n}\) et la direction tangente au choc \(U_{t}\).

On choisit un volume de contrôle entourant le choc (voir figure) et d’épaisseur fine. On intègre ensuite les équations de bilan stationnaire sur ce volume, en notant que pour la quantité de mouvement, le flux a 2 composantes. En effet le flux de quantité de mouvement à travers une surface de normale \(\overrightarrow{n}\) s’écrit:

\[\begin{split}\rho(\overrightarrow{U}\otimes\overrightarrow{U}).\overrightarrow{n}+p\overrightarrow{n}=\rho\left[\begin{array}{cc} U_{n}^{2} & U_{n}U_{t}\\ U_{n}U_{t} & U_{t}^{2} \end{array}\right]\left[\begin{array}{c} 1\\ 0 \end{array}\right]+p\left[\begin{array}{c} 1\\ 0 \end{array}\right]=\left[\begin{array}{c} \rho U_{n}^{2}+p\\ \rho U_{n}U_{t} \end{array}\right]\end{split}\]

1. bilan de masse:

   (3.12)\[\rho_{1}U_{n1}=\rho_{2}U_{n2}\]

2. bilan de quantité de mouvement suivant la normale:

   (3.13)\[\rho_{1}U_{n1}^{2}+p_{1}=\rho_{2}U_{n2}^{2}+p_{2}\]

3. bilan de quantité de mouvement suivant la tangente:

   (3.14)\[\rho_{1}U_{n1}U_{t1}=\rho_{2}U_{n2}U_{t2}\]

4. conservation de l’enthalpie totale:

   (3.15)\[h_{1}+\frac{U_{n1}^{2}+U_{t1}^{2}}{2}=h_{2}+\frac{U_{n2}^{2}+U_{t2}^{2}}{2}\]

En utilisant l’équation (3.12), la relation (3.14)implique la conservation de la vitesse tangentielle \(U_{t1}=U_{t2}\) , et on constate alors que le système d’équation est identique à celui du choc droit, en remplaçant simplement dans les équations les vitesses \(U_{1}\) et \(U_{2}\) par les vitesses normales \(U_{n1}=U_{1}\sin\beta\) et \(U_{n2}=U_{2}\sin\beta\). Les relations de choc pour un choc oblique sont données par les relations (3.7), (3.8), (3.9) en remplaçant le nombre de Mach \(M_{1}\) par le nombre de Mach « normal » \(M_{n1}=\frac{U_{n1}}{c_{1}}=M_{1}\sin\beta\) et le nombre de Mach \(M_{2}\) par le nombre de Mach « normal » \(M_{n2}=\frac{U_{n2}}{c_{2}}=M_{2}\sin(\beta-\theta)\).

De cette analogie avec le choc droit, on en déduit que pour un choc oblique, le Mach « normal » aval \(M_{n2}\) doit être subsonique, mais l’écoulement aval peut rester supersonique (et le reste en général).

L’angle de déflection de l’écoulement \(\theta\) vérifie:

\[\theta=\beta-\tan^{-1}\frac{U_{n_{2}}}{U_{t}}=\tan^{-1}\frac{U_{n_{1}}}{U_{t}}-\tan^{-1}\frac{U_{n_{2}}}{U_{t}}\]

Pour une valeur \(U_{n1}\) et \(U_{n2}\) fixée, i.e. une intensité de choc fixé, la courbe \(\theta(U_{t})\) présente un maximum pour \(U_{t}=\sqrt{U_{n1}U_{n2}}\). Cela veut dire que pour une intensité de choc donnée, il existe une valeur maximale de la déflexion \(\theta_{max}\) . Ainsi pour un nombre de Mach \(M_{1}=3\) , on a \(\theta_{max}=36^{\circ}\).

Si on trace le diagramme de vitesse \(\frac{U_{2}}{U_{1}}\) pour un nombre de Mach amont \(M_{1}\) fixé, dans des axes \(\frac{U_{2x}}{U_{1}}\)(projection suivant l’axe \(x\) parallèle à \(U_{1}\)) et \(\frac{U_{2y}}{U_{1}}\)(projection suivant l’axe \(y\)), on obtient une polaire des vitesses pour le choc oblique.

Remarque: on a \(\frac{U_{n2}}{U_{n1}}=F(M_{1},\beta)\) d’après (3.7), et \(U_{t2}=U_{t1}=U_{1}\cos\beta\), d’où l’on déduit par projection suivant les axes \(Ox\) et \(Oy\) les composantes de \(U_{2}\) : \(\frac{U_{2x}}{U_{1}}=F(M_{1},\beta)\) et \(\frac{U_{2y}}{U_{1}}=G(M_{1},\beta)\) . Pour une valeur fixé de \(M_{1}\), on en déduit donc pour chaque valeur de \(\beta\) (angle du choc) les composantes de la vitesse avale \(U_{2}\), et donc l’angle de déflexion \(\theta=arctg\frac{U_{2y}}{U_{2x}}\).

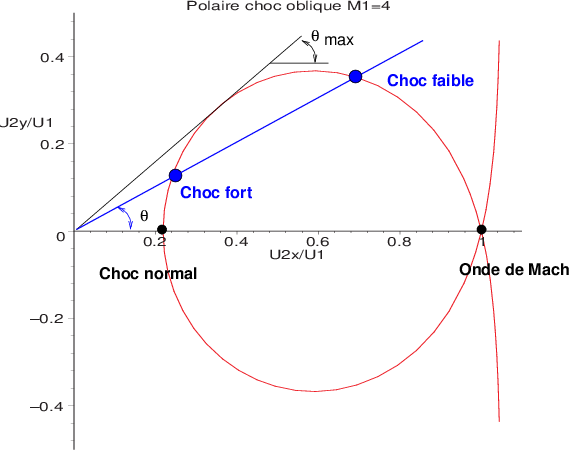
Fig. 3.22 polaire des angles pour un choc oblique

Sur cette polaire, on constate que pour un angle de déviation \(\theta\) donné, il existe 2 solutions:

1. un choc faible correspondant à la vitesse \(U_{2}\) la plus grande: la décélération du fluide est dans ce cas la plus faible et l’écoulement reste en général supersonique après le choc. C’est la configuration que l’on rencontre le plus souvent.

2. un choc fort correspondant à la vitesse \(U_{2}\) la plus faible: la décélération du fluide est plus forte et l’écoulement est alors subsonique après le choc.

On note aussi sur le diagramme, l’existence d’une valeur maximale \(\theta_{max}\) de la déflexion. Dans le cas où on veut imposer une déflexion de l’écoulement avec une valeur supérieure à \(\theta_{max}\), cela ne peut plus se faire avec un choc oblique faible attaché, mais à travers un choc courbe fort détaché (voir ci dessous).

Fig. 3.23 choc faible attaché et choc fort détaché

---

1(1,2)

Une erreur dans la première version (inversion des termes signalée par Adrien Robert), a été corrigée.