2. Écoulements compressibles 1D

2.1. Écoulement 1D

Les équations de bilan pour un écoulement adiabatique 1D d’un gaz parfait s’écrivent

\[\begin{split}\begin{aligned} \frac{\partial\rho}{\partial t}+\frac{\partial\rho u}{\partial x} & = & 0\\ \frac{\partial\rho u}{\partial t}+\frac{\partial\rho u^{2}}{\partial x}+\frac{\partial p}{\partial x} & = & 0\\ \frac{\partial}{\partial t}(\rho e+\frac{1}{2}\rho u^{2})+\frac{\partial(\rho e+\frac{1}{2}\rho u^{2}+p)u}{\partial x} & = & 0\end{aligned}\end{split}\]

A ces équations on ajoute l’équation d’état des gaz parfaits:

\[e=\frac{1}{\gamma-1}\frac{p}{\rho}\]

Si l’écoulement est isentropique (i.e. thermodynamiquement réversible), on remplace l’équation de bilan d’énergie par la relation \((S=cste)\) i.e.:

\[p/\rho^{\gamma}=cste\]

2.2. Vitesse de propagation

Considérons tout d’abord la propagation d’une perturbation de pression \(dp\) dans un tuyau de section constante contenant un gaz au repos. Cette onde sonore se propage avec une célérité \(c\). L’apparition d’une perturbation de pression engendre une augmentation \(du\) de la vitesse du gaz, perturbation qui se propage aussi à la célérité \(c.\) Considérons un volume de contrôle \(AB\) qui suit le front de la perturbation \(C\) (figure ci dessous)

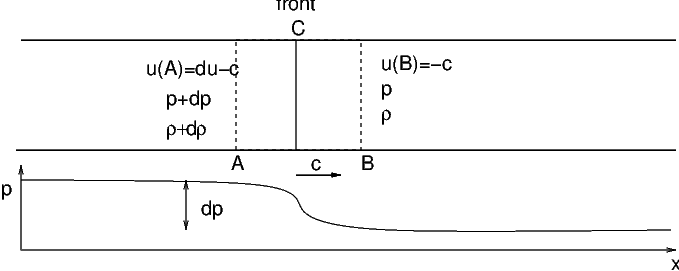
Fig. 2.28 propagation d’une perturbation

Ce volume de contrôle se déplace à la vitesse \(c\) par rapport à un référentiel fixe et l’écoulement relatif peut être considéré comme stationnaire en temps. Donc dans la section \(B\) après le front (fluide au repos), la vitesse relative vaut \(u_{B}=-c\) , la pression \(p\) et la masse volumique \(\rho,\) et dans la section \(A\) avant le front, la vitesse relative du fluide vaut \(u_{A}=du-c\), la pression \(p+dp\) et la masse volumique \(\rho+d\rho\).

L’équation de bilan de la masse intégrée entre \(A\) et \(B\) s’écrit:

\[(du-c)*(\rho+d\rho)=-c*\rho\]

d’où au premier ordre l’accroissement de vitesse:

\[du=c\frac{d\rho}{\rho}\]

De la même façon l’équation de bilan de la quantité de de mouvement intégrée entre \(A\) et \(B\) s’écrit:

\[(\rho+d\rho)(du-c)^{2}+(p+dp)=\rho c^{2}+p\]

et en ne conservant que les termes au premier ordre

\[dp+c^{2}d\rho=2\rho c\,du\]

et en remplaçant \(du\), on obtient- l’expression de la célérité de l’onde de pression:

\[c^{2}=(\frac{dp}{d\rho})\]

Cette expression de la célérité des ondes est en fait générale (i.e. ne dépend pas du type de gaz), à condition de noter que l’expression trouvée suppose des petites perturbations (i.e. un écoulement isentropique). Dans ce cas, on a pour un gaz :

\[c^{2}=\left(\frac{\partial p}{\partial\rho}\right)_{s=cste}\]

Pour un gaz parfait, on a montré que l’écoulement isentropique vérifiait

\[\frac{p}{\rho^{\gamma}}=cste\]

ce qui nous donne l’expression de la célérité des ondes dans un gaz parfait

\[c^{2}=\gamma\frac{p}{\rho}=\gamma RT\]

qui dépend donc de \(\sqrt{T}\). Pour de l’air à température ambiante \(T=320\,K\), \(R=287\), \(\gamma=1.4\) la vitesse du son vaut \(c=360\,m/s\)

Remarque: pour un écoulement isentropique, on peut remplacer l’équation de bilan de l’énergie par la relation (valable pour n’importe quel gaz):

\[c^{2}=\frac{dp}{d\rho}\]

2.3. Ondes sonores

On considère une perturbation de pression \(p'(x,t)\) dans un écoulement d’air stationnaire en moyenne (\(U_{0},\) \(p_{0},\rho_{0}\)). Cette perturbation induit une perturbation de masse volumique \(\rho'\) et de vitesse \(u'\). La pression \(p_{0}+p'\) , la masse volumique \(\rho_{0}+\rho'\) et la vitesse \(\textrm{U}_{0}+u'\) sont solutions des équations d’Euler. De plus les fluctuations étant faibles, l’écoulement est isentropique et on néglige les fluctuations devant les valeurs moyennes \(U_{0},\rho_{0}\) et \(p_{0}\) en ne conservant que les termes d’ordre 1.

En se plaçant dans un référentiel en translation uniforme \(U_{0}\), la fluctuation \(p'\) est solution de l’équation des ondes:

\[\frac{\partial^{2}p'}{\partial t^{2}}-\frac{\gamma p_{0}}{\rho_{0}}\frac{\partial^{2}p}{\partial x^{2}}=0\]

La fluctuation de vitesse \(u'\) est définie par:

\[\frac{\partial u'}{\partial t}=-\frac{1}{\rho_{0}}\frac{\partial p'}{\partial x}\]

et la fluctuation de masse volumique \(\rho'\):

\[\rho'=\frac{\rho_{0}}{\gamma}\frac{p'}{p_{0}}\]

Cette équation des ondes décrit la propagation d’une onde de pression \(p'(x,t)\) avec une célérité \(c_{0}=\sqrt{\gamma p_{0}/\rho_{0}}\) . La solution générale de cette équation est de la forme

\[p'(x,t)=F(x-c_{0}t)+G(x+c_{0}t)\]

Les fonctions \(F\) et \(G\) sont déterminées par les conditions initiales \(p'(x,0)\) et \(\frac{\partial p'}{\partial t}(x,0)\)

Ainsi pour une perturbation sinusoïdale \(p'(x,t)=Be^{i\omega(x-c_{0}t)}\), la fluctuation de vitesse \(u'\) vaut \(u'(x,t)=\frac{1}{\rho_{0}c_{0}}Be^{i\omega(x-c_{0}t)}\), et la fluctuation de masse volumique \(\rho'(x,t)=\frac{1}{c_{0^{2}}}Be^{i\omega(x-c_{0}t)}\).

2.3.1. Ordre de grandeurs

Dans de l’air au repos \(\rho_{0}=1\,kg/m^{3}\) , \(p_{0}=10^{5}\,Pa\) , \(\gamma=1.4\) on a \(c_{0}=370\,m/s\)

Les ondes de pression ont une puissance acoustique de l’ordre de 1 à 100 db. La puissance acoustique en décibel est liée à la puissance moyenne \(w'\) de l’onde par la relation:

\[db=120+10\,log_{10}(w')\]

et la puissance moyenne \(w'\) est donné par:

\[w'=\frac{\omega c_{0}}{2\pi}\int_{0}^{\frac{\omega c_{0}}{2\pi}}p'(x,t).\overline{u'(x,t)}\,dt=\frac{B^{2}}{\rho_{0}c_{0}}\]

Cela donne l’ordre de grandeurs des amplitudes \(B\) des ondes de pression: \(B=10^{-4}\,Pa\) à \(1\,Pa\), de l’amplitude des fluctuations de vitesse \(0.3\,10^{-6}\,m/s\) à \(0.3\,10^{-2}\,m/s\) et de l’amplitude des fluctuations de masse volumique \(0.9\,10^{-9}\,kg/m^{3}\) à \(0.9\,10^{-5}\,kg/m^{3}\). On constate donc que les ondes sonores sont quasiment incompressibles. De plus le déplacement \(\xi\) des particules est très faible. En effet l’équation de la trajectoire d’une particule s’écrit:

\[\frac{d\xi}{dt}=u'(\xi,t)\,\,avec\,\,\xi(0)=x\]

En linéarisant l’équation, i.e. en approximant \(u'(\xi,t)=u'(x,t)\) , on intègre cette équation:

\[\xi=\frac{iB}{\rho_{0}\omega c_{0}^{2}}e^{i\omega(x-c_{0}t)}=\frac{1}{2\pi f}\frac{iB}{\rho_{0}c_{0}}e^{i\omega(x-c_{0}t)}\]

en notant \(f=\frac{\omega c_{0}}{2\pi}\) la fréquence temporelle de l’onde. Pour des ondes acoustiques ( \(f=10\,hz\) à \(10\,khz\)), avec \(f=330\,hz\) on obtient une amplitude du déplacement de \(0.4\,10^{-9}\,m\) à \(0.4\,10^{-5}\,m\).

2.3.1.1. Exemple de propagation d’une onde sonore

Fig. 2.29 propagation d’une onde sonore

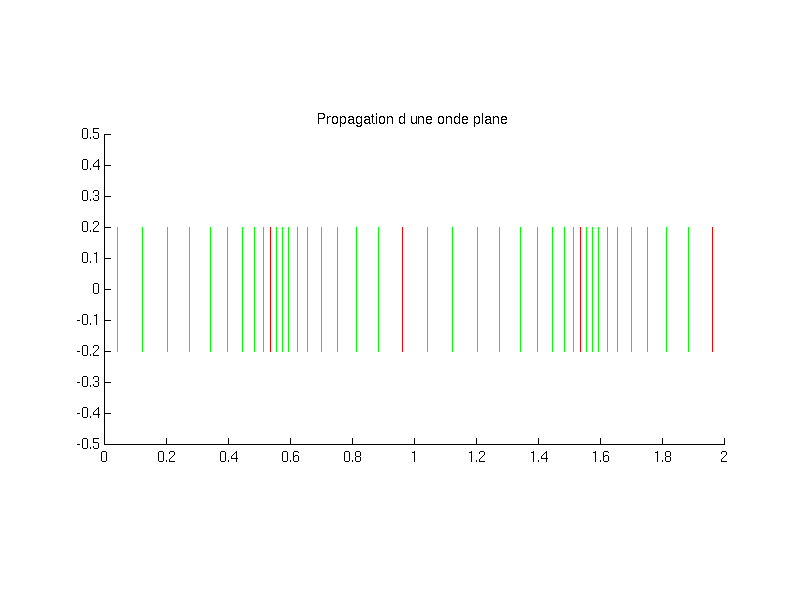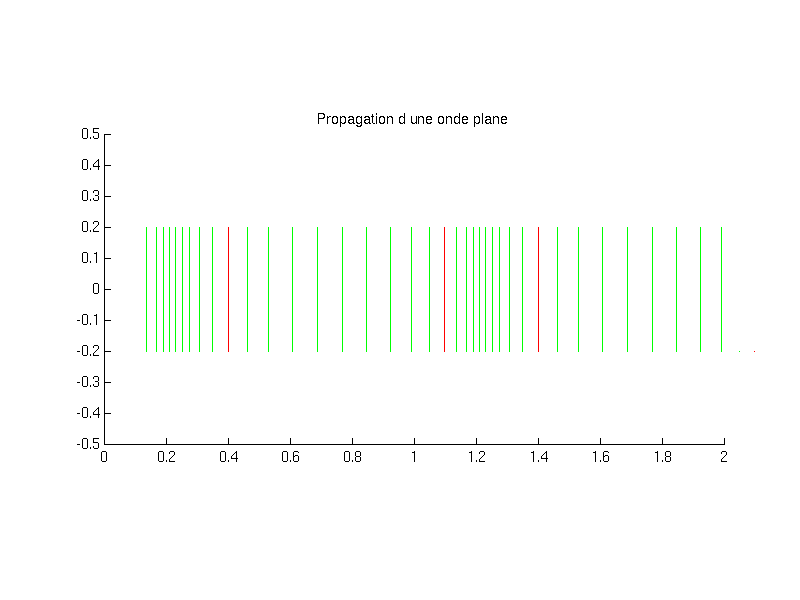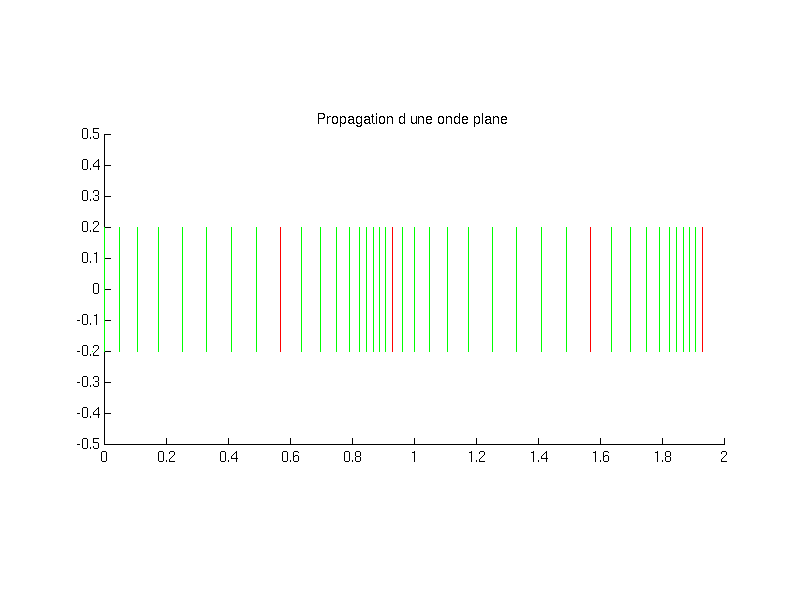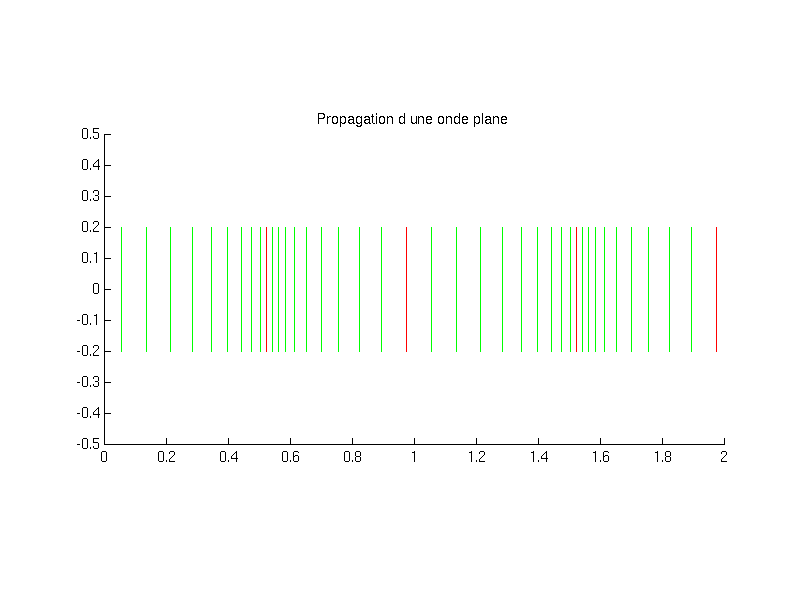
Fig. 2.30 animation de la propagation d’une onde sonore

2.3.2. Cône de Mach

On considère l’émission de perturbations (ondes sonores) par une source. Différents cas se présentent suivant que la source se déplace à une vitesse supérieure ou inférieure à la vitesse de propagation des ondes: i.e. la vitesse du son. (voir animations)

1. Si la source est immobile \(U_{0}=0\), les surfaces d’ondes sont des sphères

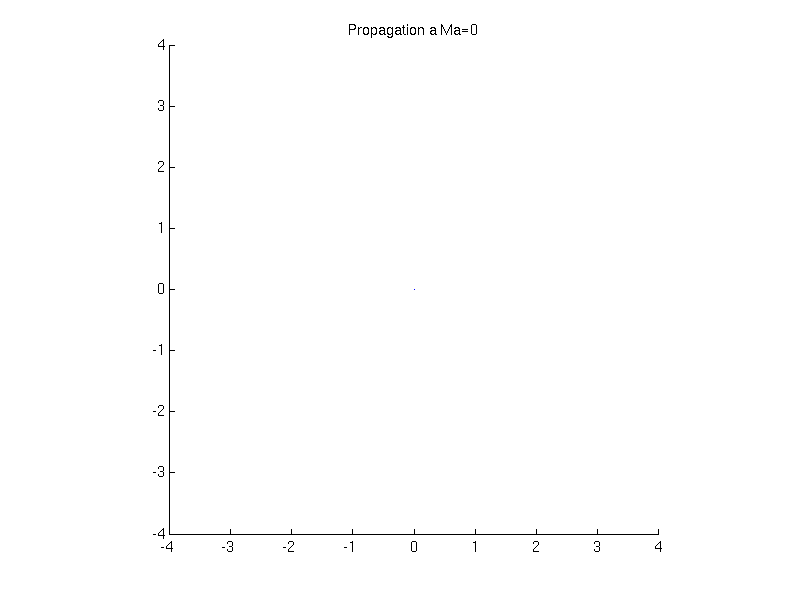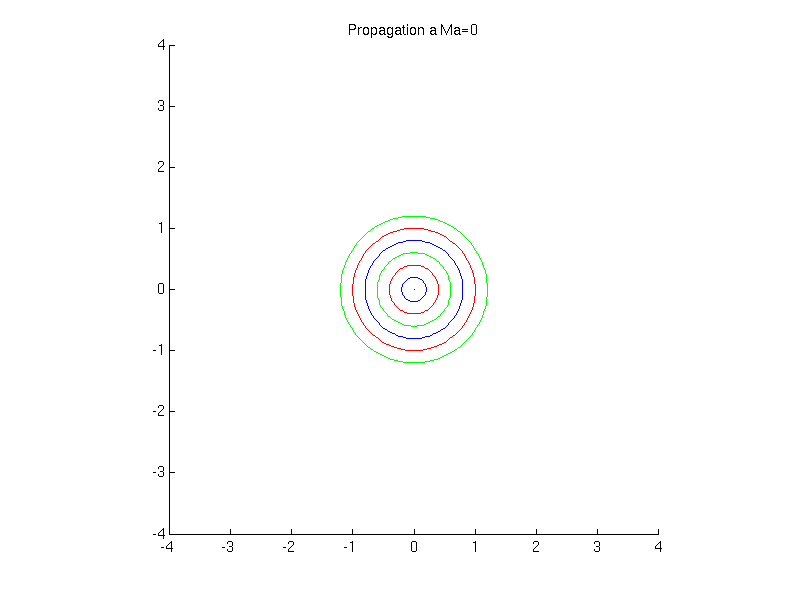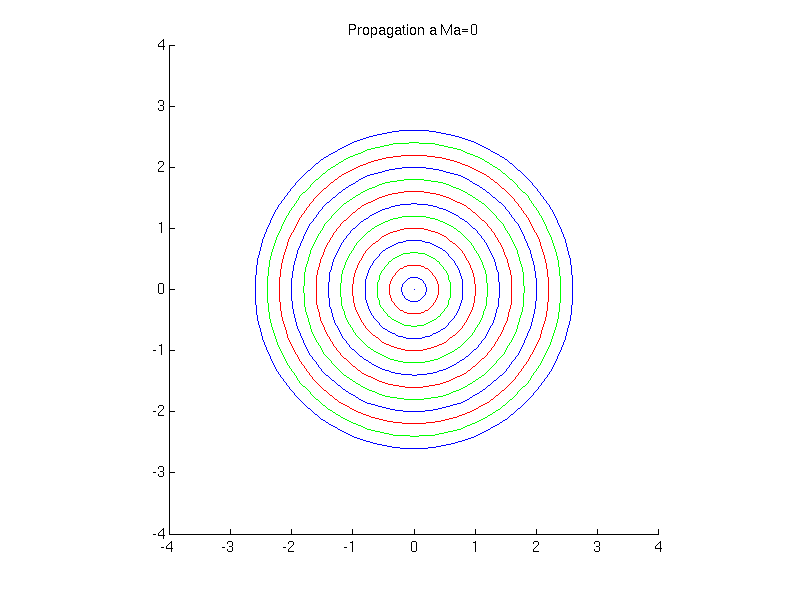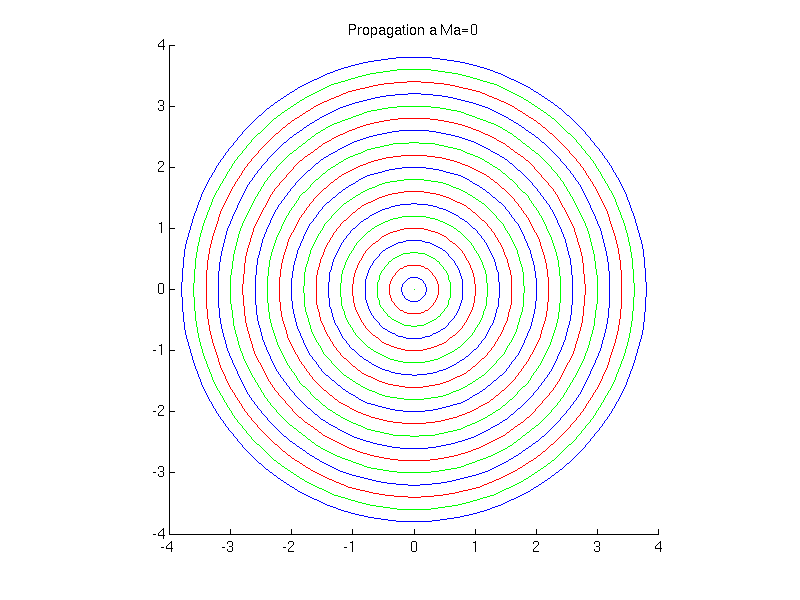
Fig. 2.31 animation de la propagation d’une onde sonore \(Ma=0\)

2. Si \(U_{0}<c_{0}\) (écoulement subsonique)

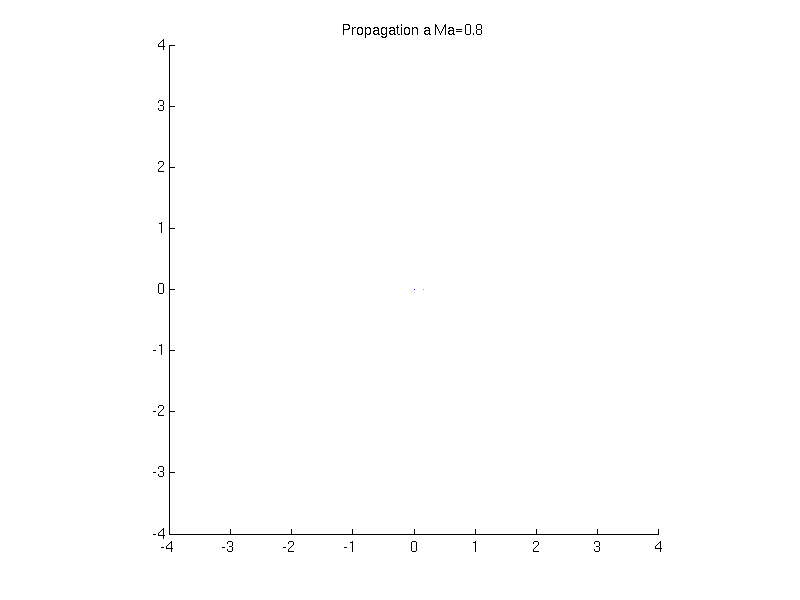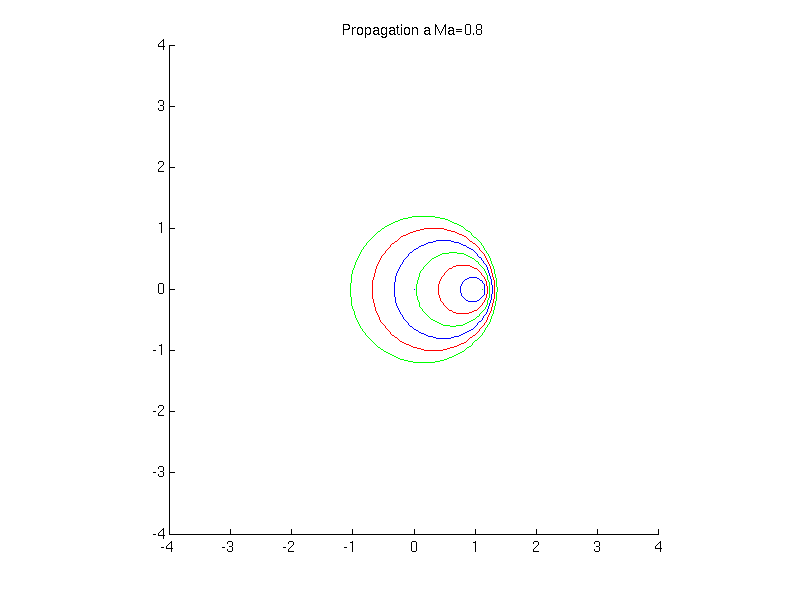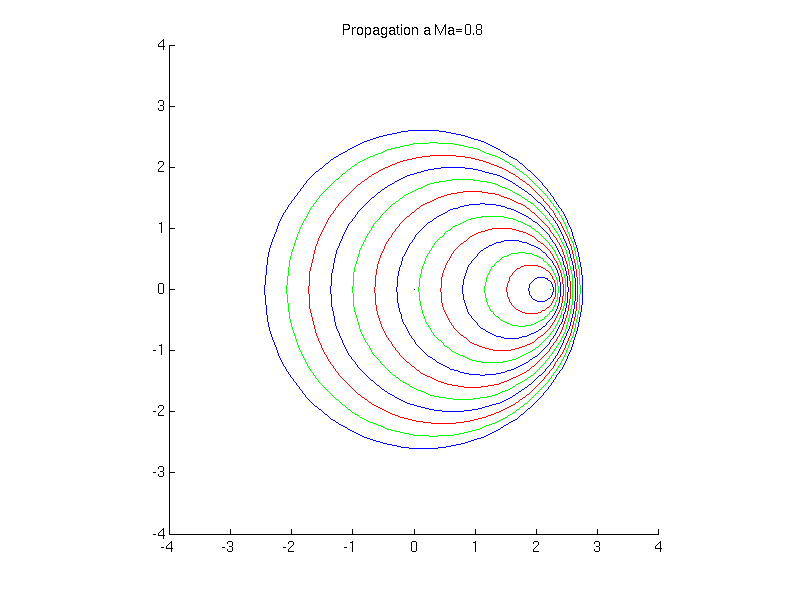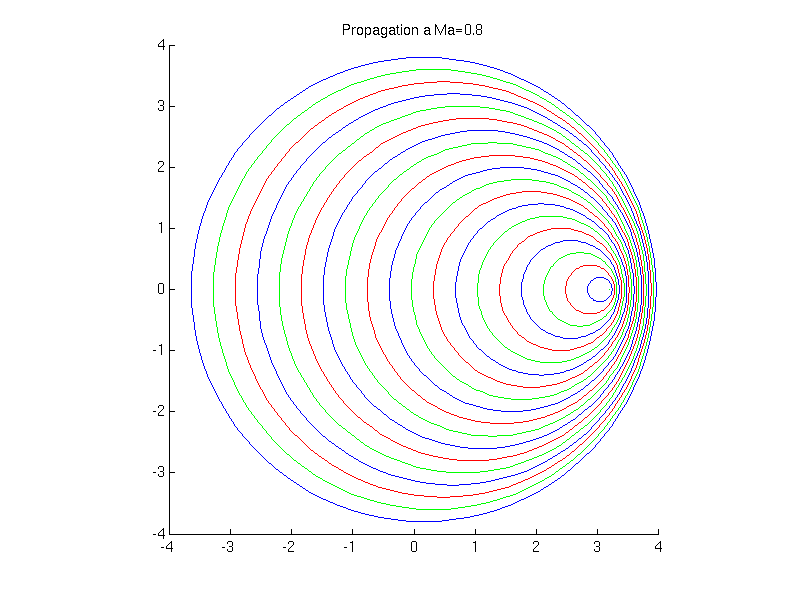
Fig. 2.32 animation de la propagation d’une onde sonore \(Ma=0.8\)

3. Si \(U_{0}=c_{0}\) (écoulement transsonique)

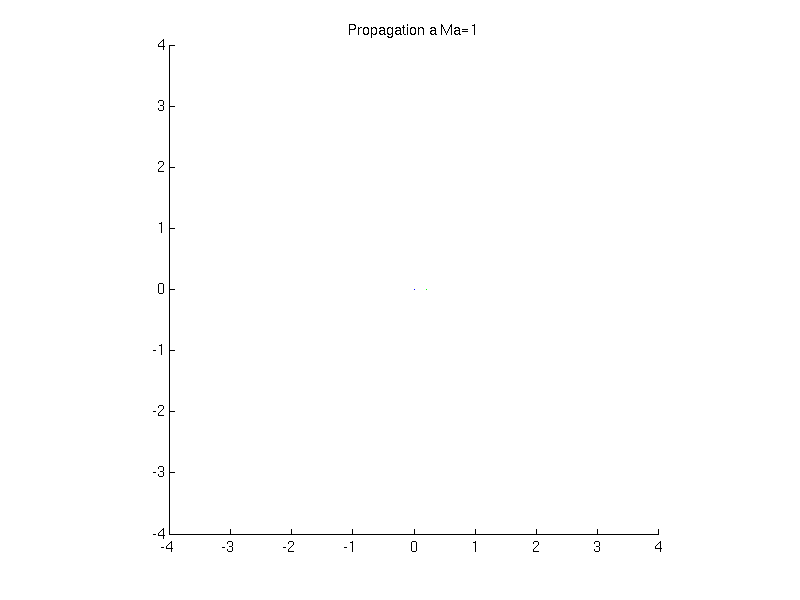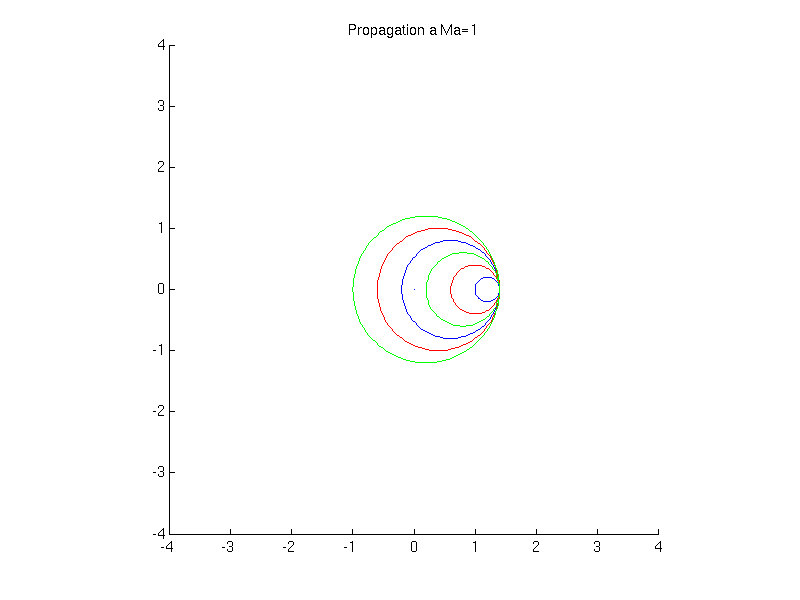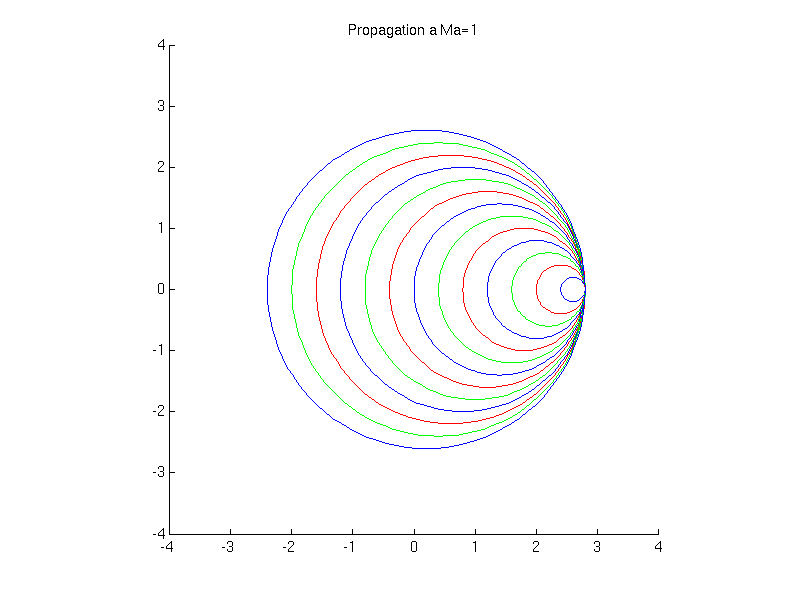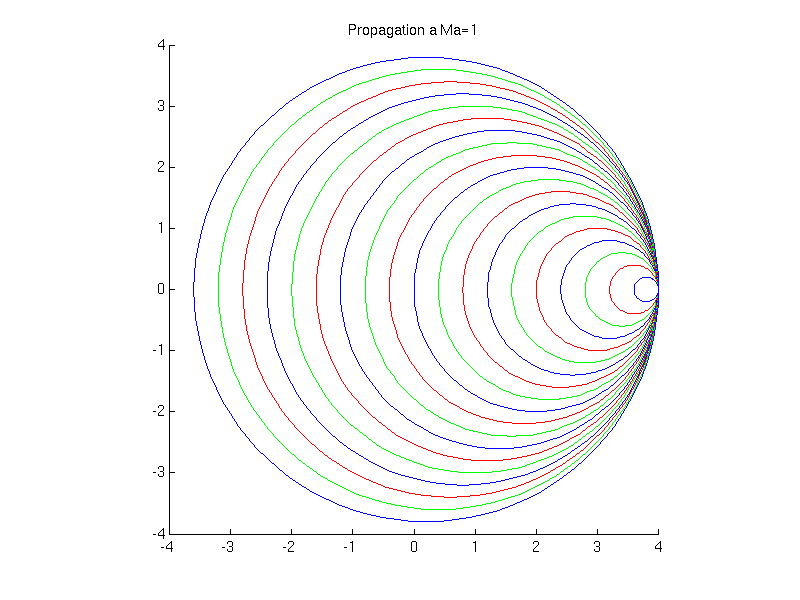
Fig. 2.33 animation de la propagation d’une onde sonore \(Ma=1\)

4. si \(U_{0}>c_{0}\) (écoulement supersonique)

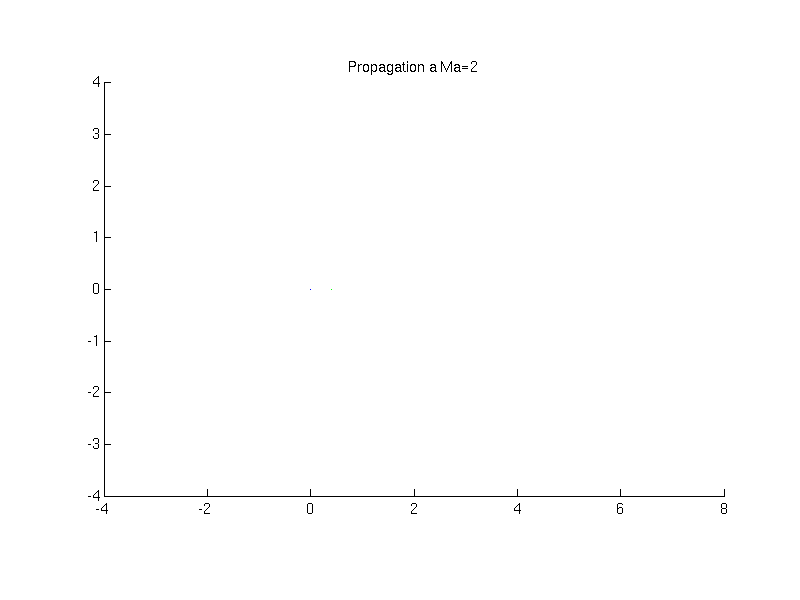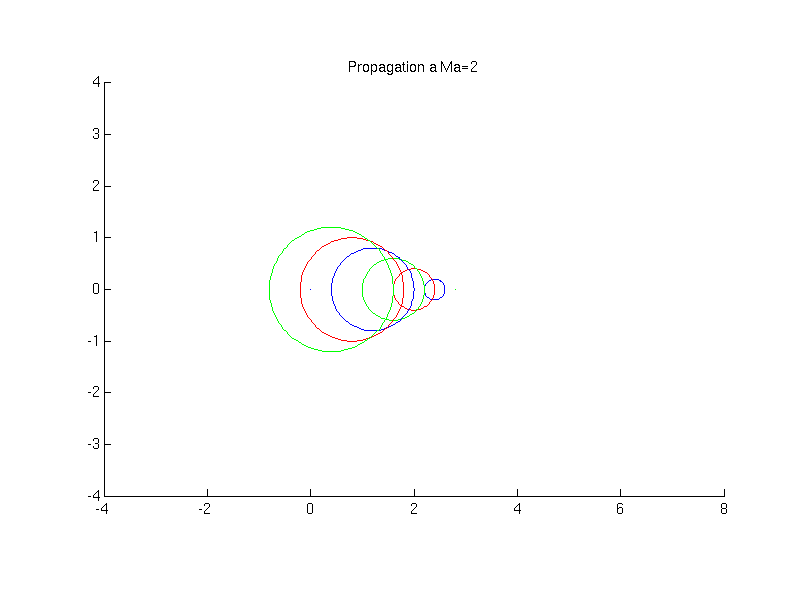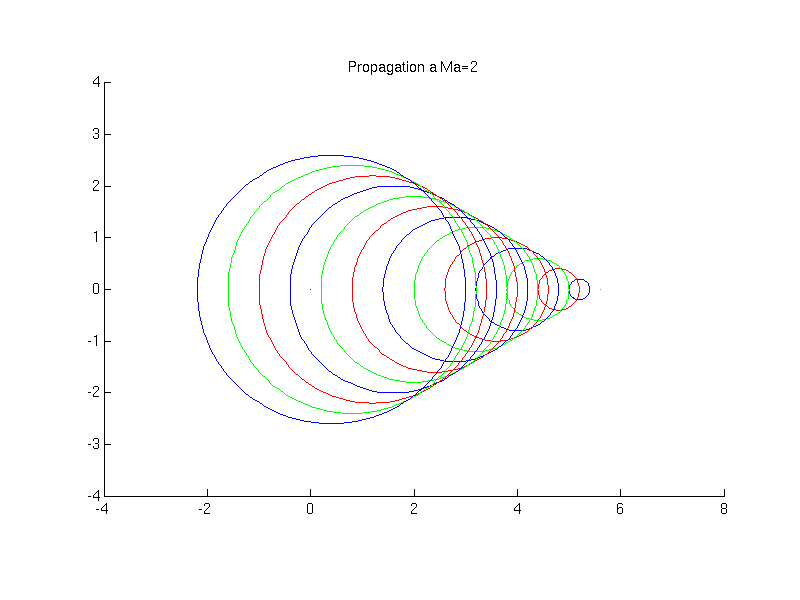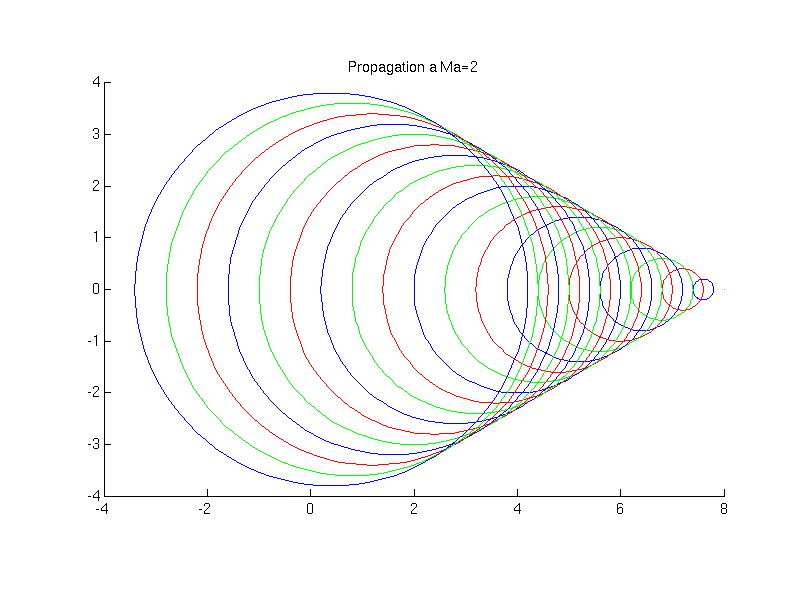
Fig. 2.34 animation de la propagation d’une onde sonore \(Ma=2\)

Dans ce dernier cas, la source se déplace plus vite que l’onde, qui reste contenu dans un cône à l’arrière de la source, que l’on appelle cône de Mach. Le demi angle au sommet \(\alpha\) du cône vérifie:

\[sin\,\alpha=\frac{c_{0}}{u_{0}}=Ma^{-1}\]

Cet angle est inversement proportionnel au nombre de Mach \(Ma=\frac{u_{0}}{c_{0}}\)

Dans l’animation suivante, on modélise le champ de pression généré par un dipôle harmonique se déplaçant à une vitesse supersonique constante. On visualise le champ de pression généré par le dipôle.

Fig. 2.35 propagation sonore supersonique

2.4. Équations caractéristiques

Les équations d’Euler forment un système hyperbolique, caractéristique d’un phénomène de propagation. Pour étudier les propriétés de ce système, nous considérerons un écoulement compressible instationnaire 1D isentropique. Le système d’équations s’écrit

\[\begin{split}\begin{aligned} \frac{\partial\rho}{\partial t}+\frac{\partial\rho u}{\partial x} & = & 0\\ \frac{\partial\rho u}{\partial t}+\frac{\partial\rho u^{2}}{\partial x}+\frac{\partial p}{\partial x} & = & 0\end{aligned}\end{split}\]

avec la relation isentropique

(2.18)\[p/\rho^{\gamma}=cste=K\]

Nous allons transformer ce système en éliminant \(p\) et \(\rho,\) pour ne conserver que 2 variables \(u\) et \(c=\sqrt{\frac{\gamma p}{\rho}}\).

D’après la relation (2.18), on déduit la relation entre \(\rho\) et \(c\):

\[c^{2}=K\gamma\rho^{\gamma-1}\,\,\mbox{ soit }\,log(\rho)=\frac{2}{\gamma-1}log(c)+cste\]

d’où

\[\frac{d\rho}{\rho}=\frac{2}{\gamma-1}\frac{dc}{c}\]

En remplaçant \(d\rho\) dans l’équation de bilan de la masse

\[\frac{\partial\rho}{\partial t}+u\frac{\partial\rho}{\partial x}+\rho\frac{\partial u}{\partial x}=0\]

on obtient une équation sur \(u\) et \(c\)

(2.19)\[\frac{2}{\gamma-1}\frac{\partial c}{\partial t}+\frac{2u}{\gamma-1}\frac{\partial c}{\partial x}+c\frac{\partial u}{\partial x}=0\]

De même en remplaçant dans l’équation de quantité de mouvement:

\[\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+\frac{1}{\rho}\frac{\partial p}{\partial x}=0\]

\(dp=c^{2}d\rho\) on obtient

(2.20)\[\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+\frac{2c}{\gamma-1}\frac{\partial c}{\partial x}=0\]

En additionnant (2.19) et (2.20) et en soustrayant (2.19) et (2.20), on obtient les 2 équations caractéristiques:

\[\begin{split}\begin{aligned} \left\{ \frac{\partial}{\partial t}+(u+c)\frac{\partial}{\partial x}\right\} (+u+\frac{2}{\gamma-1}c) & = & 0\\ \left\{ \frac{\partial}{\partial t}+(u-c)\frac{\partial}{\partial x}\right\} (-u+\frac{2}{\gamma-1}c) & = & 0\end{aligned}\end{split}\]

Posons \(r=u+\frac{2c}{\gamma-1}\) et \(s=-u+\frac{2c}{\gamma-1}\) (invariants de Riemann), le système s’écrit:

\[\begin{split}\begin{aligned} \frac{\partial r}{\partial t}+(u+c)\frac{\partial r}{\partial x} & = & 0\\ \frac{\partial s}{\partial t}+(u-c)\frac{\partial s}{\partial x} & = & 0\end{aligned}\end{split}\]

dont l’interprétation est la suivante: soit \(\Gamma^{+}\)la famille de courbes de pente \(\frac{dx}{dt}=u+c\) et \(\Gamma^{-}\)celle de pente \(\frac{dx}{dt}=u-c\), les solutions \(r\) et \(s\) vérifient

1. \(r=cste\) le long des courbes \(\Gamma^{+}\)

2. \(s=cste\) le long des courbes \(\Gamma^{-}\)

En effet soit \(\xi\) l’abscisse curviligne le long de la courbe \(\Gamma^{+}\) de pente \(\frac{dx}{dt}=u+c\), on a

\[\frac{dr}{d\xi}=\frac{\partial r}{\partial t}\frac{dt}{d\xi}+\frac{\partial r}{\partial x}\frac{dx}{d\xi}=\left(\frac{\partial r}{\partial t}+\frac{\partial r}{\partial x}(u+c)\right)\frac{dt}{d\xi}=0\]

Connaissant les courbes caractéristiques, on peut alors en déduire la solution en tout point.

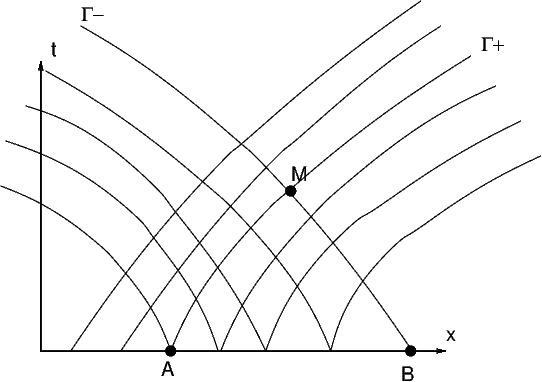
Fig. 2.36 courbes caractéristiques

Soit \(M=(x,t)\) un point quelconque du plan \((x,t)\), il se trouve à l’intersection de 2 caractéristiques: \(\Gamma^{+}\) issue de \(A=(x_{A},0)\) et \(\Gamma^{-}\) issue de \(B=(x_{B},0)\). On a donc:

\[r(M)=r(A)\,\mbox{ et }\,s(M)=s(B)\]

Connaissant \(r\) et \(s\) on en déduit l’état du fluide en \(M\).

Cette démarche attractive possède cependant un inconvénient majeur: on ne sait pas en général déterminer les courbes caractéristiques \(\Gamma^{+}\) et \(\Gamma^{-}\), car elles dépendent de la solution ! Cependant cette approche nous informe sur les propriétés des équations d’Euler pour un écoulement de gaz:

1. ces équations traduisent une propagation (équations hyperboliques)

2. les vitesses de propagation sont \(u+c\) et \(u-c\) ( et \(u\) dans le cas général)

3. la vitesse de propagation n’est pas forcement constante et dépend de la solution (problème non linéaire)

4. pour les petites perturbations (ondes acoustiques) \(u\ll c\) et la vitesse de propagation vaut \(\pm c\)

5. le sens de propagation change suivant le signe de \(u-c\)

6. certaines quantités (invariants de Riemann) se conservent le long des caractéristiques

7. ces équations peuvent générées des discontinuités (chocs), comme on le verra dans la suite

2.4.1. Création des discontinuités

Considérons un écoulement d’air se déplaçant à la vitesse \(2U_{0}\) dans un milieu initialement au repos, correspondant au champ de vitesse initial continu:

(2.21)\[u(x,0)=U_{0}(1-\tanh\frac{x}{l})\]

La répartition de pression et de masse volumique à l’instant initial est telle que la célérité du son \(c(x,t)\) vérifie:

\[c(x,0)=\frac{\gamma-1}{2}u(x,0)+c_{0}\]

i.e. on a pour \(x>2l\) un fluide au repos, avec une pression \(p_{0}\) et une masse volumique \(\rho_{0}\) t.q. \(c_{0}^{2}=\frac{\gamma\,p_{0}}{\rho_{0}}\), pour \(x<-2l\) un fluide en mouvement à la vitesse \(2U_{0}\) (avec \(2U_{0}<c_{0}\) écoulement initial subsonique), avec une pression \(p_{1}\) et une masse volumique \(\rho_{1}\) t.q. \((c_{0}+(\gamma-1)U_{0})^{2}=\frac{\gamma\,p_{1}}{\rho_{1}}\), et entre \(-2l<x<2l\) une transition continue en tangente hyperbolique \(\tanh\frac{x}{l}\) (rq \(\tanh2\simeq0.96\) ).

Avec ces conditions initiales, les invariants de Riemann ont pour valeurs:

\[s(x,0)=\frac{2}{\gamma-1}c(x,0)-u(x,0)=\frac{2}{\gamma-1}c_{0},\,\mbox{\, et\, }\,r(x,0)=2U_{0}(1-\tanh\frac{x}{l})+\frac{2}{\gamma-1}c_{0}\]

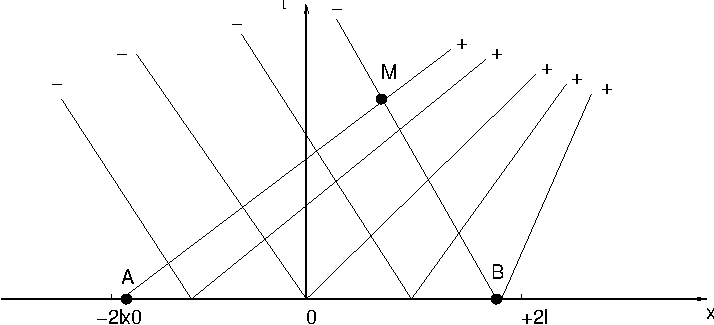
Fig. 2.37 schéma des courbes caractéristiques

D’après ce qui précède, \(s\) est constant le long des courbes caractéristiques \(\Gamma^{-}\) qui sont issue de l’axe \(Ox\) . Or \(s\) est constant à l’instant initial (i.e. sur l’axe \(Ox\) ), donc \(s\) doit être constant dans tout le plan \((x,t)\)

Pour un point M du plan, on a (voir schéma):

\[s(M)=\frac{2}{\gamma-1}c_{0},\,\mbox{\, et\, }\,r(M)=2U_{0}(1-\tanh\frac{x_{0}}{l})+\frac{2}{\gamma-1}c_{0}\]

Or d’après la définition de \(r\) et \(s\) on a: \(u=\frac{1}{2}(r-s)\) et \(c=\frac{\gamma-1}{2}(r+s)\), \(s\) étant constant dans la plan et \(r\) étant constant le long des courbes \(\Gamma^{+}\), on en déduit que \(u\) et \(c\) sont forcément constants le long des courbes \(\Gamma^{+}\). Or les courbes \(\Gamma^{+}\) ont pour pente \(u+c\) , ce sont donc des droites. La courbe \(\Gamma^{+}\) issue de \(A\) est la droite d’équation \(x=(u(x_{A},0)+c(x_{A},0))*t+x_{A}\). La famille des droites \(\Gamma^{+}\) a pour pente:

(2.22)\[\frac{dt}{dx}=\left(\frac{\gamma+1}{2}U_{0}(1-\tanh\frac{x_{0}}{l})+c_{0}\right)^{-1}=m_{0}^{-1}\]

Pour \(x<-2l\) , la pente devient constante (\(\sim\left((\gamma+1)U_{0}+c_{0}\right)^{-1}\)) et les caractéristiques sont parallèles, et de même pour \(x>2l\) (la pente vaut \(\sim c_{0}^{-1}\)). Entre les deux la pente varie continûment et les courbes caractéristiques \(\Gamma^{+}\) doivent se rejoindre au bout d’un temps \(t_{s}\) (intersection des droites issues de \(x=-2l\) et \(x=+2l\)

\[t_{s}\simeq\frac{4l}{(\gamma+1)U_{0}}\]

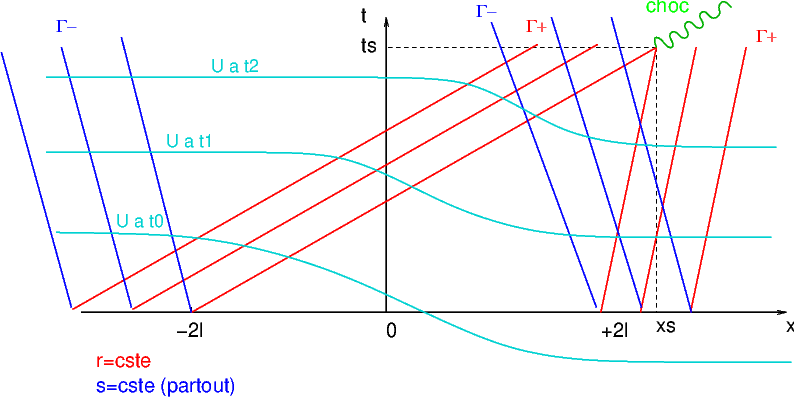
Fig. 2.38 intersection des courbes caractéristiques

Or lorsque des caractéristiques de la même famille se coupent, la solution ne peut plus rester continue, et une discontinuité doit apparaître. L’hypothèse d’écoulement isentropique n’est plus vérifiée et on a apparition d’un choc de compression.

Les courbes caractéristiques ont pour équation (avec les notations (2.22):

\[x-m_{0}t=x_{0}\]

On a montré que \(u(x,t)\) était constant le long de ces caractéristiques, donc \(u(x,t)=F(x-m_{0}t)\)

Connaissant la solution initiale \(u(x,t=0)\) (2.21), on en déduit la solution \(u(x,t)\)

\[u(x,t)=U_{0}(1-\tanh\frac{x-m_{0}t}{l})\]

et la solution \(c(x,t)\)

\[c(x,t)=\frac{\gamma-1}{2}U_{0}(1-\tanh\frac{x-m_{0}t}{l})+c_{0}\]

On note que \(m_{0}\) (2.22) vérifie:

\[m_{0}=u(x,0)+c(x,0)=u(x,t)+c(x,t)\]

La solution est donc une onde qui se propage à la vitesse absolue \(m_{0}\) , c’est à dire à la vitesse \(c(x,t)\) relativement au fluide. La vitesse de propagation des perturbation par rapport au fluide est donc bien \(c(x,t)\), la célérité du son locale. Pour une perturbation faible \(U_{0}\ll c_{0}\), on retrouve l’approximation de l’acoustique avec des ondes se propageant avec une célérité constante \(c_{0}\).

Cette analyse est confirmée par une résolution numérique des équations d’Euler, dont la solution au cours du temps est tracée ci dessous.

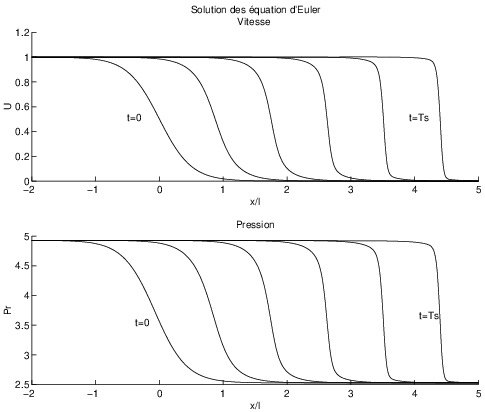
Fig. 2.39 ondes de compression

Si on considère une onde de détente, i.e. une perturbation correspondant à un champ de vitesse opposé au précédent:

\[u(x,0)=U_{0}(1+\tanh\frac{x}{l})\]

la perturbation s’évanouit au cours du temps, puisque les courbes caractéristiques divergent (voir figure ci dessous)

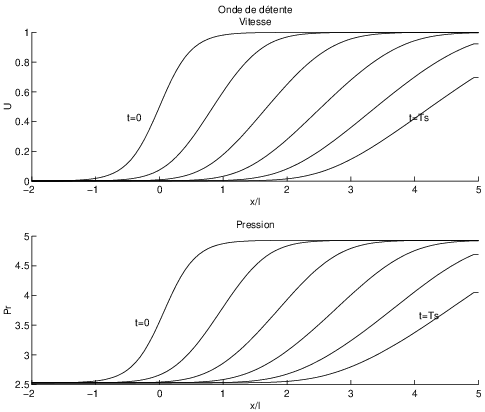
Fig. 2.40 ondes de détente

2.5. Écoulement quasi 1D en conduite

On considère un écoulement quasi-1D dans une conduite de section \(S(x)\) variable. On suppose que la variation de section \(S\) est suffisamment faible pour que l’écoulement soit uni-dimensionnel avec une vitesse \(U(x,t)\).

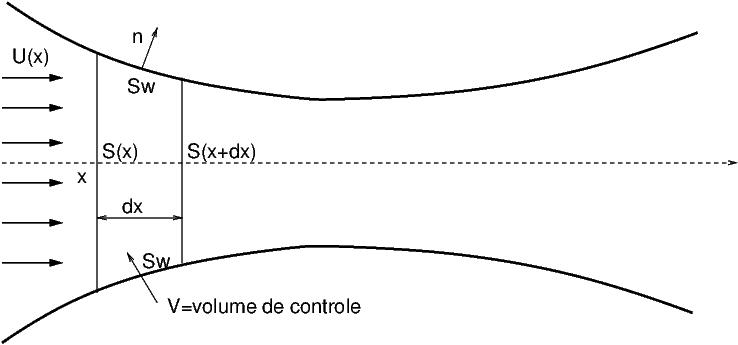
Fig. 2.41 écoulement en tuyère

On considère le volume de contrôle \(V\) de la figure ci-dessus, limité par les sections \(S(x)\) et \(S(x+dx)\)

Les équations de bilan d’un gaz parfait compressible (voir chapitre 1) intégrées sur le volume \(V\) de frontière \(\Gamma\) s’écrivent (après utilisation du théorème de la divergence):

\[\begin{split}\begin{aligned} \int_{V}(\frac{\partial\rho}{\partial t}+div(\rho\overrightarrow{U}))\,dV= & \int_{V}\frac{\partial\rho}{\partial t}dV+\int_{\Gamma}\rho\overrightarrow{U}.\overrightarrow{n}\,dS & =0\\ \int_{V}(\frac{\partial\rho\overrightarrow{U}}{\partial t}+div(\rho\overrightarrow{U}\otimes\overrightarrow{U}+p\,\overline{\overline{Id}}))\,dV= & \int_{V}\frac{\partial\rho\overrightarrow{U}}{\partial t}dV+\int_{\Gamma}((\rho\overrightarrow{U}\otimes\overrightarrow{U}).\overrightarrow{n}+p\overrightarrow{n})\,dS & =0\\ \int_{V}\frac{\partial E_{t}}{\partial t}+div(\overrightarrow{U}H_{t})= & \int_{V}\frac{\partial E_{t}}{\partial t}dV+\int_{S}H_{t}\overrightarrow{U}.\overrightarrow{n}\,dS & =0\end{aligned}\end{split}\]

On a noté \(E_{t}=\rho e+\frac{1}{2}\rho U^{2}\) l’énergie totale par unité de volume, et \(H_{t}=E_{t}+p\) l’entalpie totale.

A ces équations, on rajoute l’équation d’état des gaz parfaits:

\[e=\frac{1}{\gamma-1}\frac{p}{\rho}\]

Le volume \(V\) considéré est égal au premier ordre en x à \(V\simeq S\,dx\), donc les intégrales de volume d’une fonction \(f(x)\) s’écrivent:

\[\int_{V}f(x)\,dV\simeq f(x)\,S\,dx\]

Les intégrales de surface d’une fonction \(F(x)\) se décomposent en intégrale sur les sections débitantes \(S(x)\) et \(S(x+dx)\) , et sur la frontière pariétale \(S_{w}\):

\[\begin{split}\begin{aligned} \int_{\Gamma}F(x)\,dS= & \int_{S(x)}F(x)\,dS+\int_{S(x+dx)}F(x+dx)\,dS+\int_{S_{w}}F(x)\,dS\\ = & F(x)S(x)+F(x+dx)S(x+dx)+\int_{S_{w}}F(x)\,dS\end{aligned}\end{split}\]

Pour l’équation de bilan de la masse, \(F(x)=\rho\overrightarrow{U}.\overrightarrow{n}\) est nulle sur les frontières pariétales et vaut \(+\rho U(x+dx)\) en \(S(x+dx)\) et \(-\rho U(x)\) en \(S(x)\) (la normale \(\overrightarrow{n}\) est toujours dirigée vers l’extérieur du volume de contrôle). On obtient alors:

\[\frac{\partial\rho}{\partial t}S(x)dx+\rho(x+dx)U(x+dx)S(x+dx)-\rho(x)U(x)S(x)=0\]

soit au premier ordre en x:

(2.23)\[S\frac{\partial\rho}{\partial t}+\frac{\partial}{\partial x}(\rho US)=0\]

Pour l’équation de bilan de quantité de mouvement, \(F(x)\)

\[F(x)=\left((\rho\overrightarrow{U}\otimes\overrightarrow{U}+p\,\overline{\overline{Id}}).\overrightarrow{n}\right).\overrightarrow{e_{x}}\]

est la composante suivant \(Ox\) qui est non nulle sur les frontières pariétales et vaut \(p\,n_{x}\) où \(n_{x}=\overrightarrow{n}.\overrightarrow{e_{x}}\) est la composante suivant \(Ox\) de la normale à la frontière. L’intégrale sur la paroi s’écrit au premier ordre en x:

\[\int_{S_{w}}p\,n_{x}dS\simeq\frac{p(x+dx)+p(x)}{2}\int_{S_{w}}n_{x}dS=\frac{p(x+dx)+p(x)}{2}(S(x)-S(x+dx))\]

Sur \(S(x)\), \(F(x)\) vaut \(-\rho U^{2}-p\) et sur \(S(x+dx)\) \(F(x+dx)\) vaut \(+\rho U^{2}+p\), et l’équation de bilan de la quantité de mouvement s’écrit:

\[\frac{\partial\rho U}{\partial t}S(x)\,dx+(\rho U^{2}+p)S(x+dx)-(\rho U^{2}+p)S(x)+\frac{p(x+dx)+p(x)}{2}(S(x)-S(x+dx))=0\]

ce qui donne au premier ordre en x:

\[\frac{\partial\rho U}{\partial t}S(x)+\frac{\partial}{\partial x}(\rho U^{2}S)+\frac{\partial}{\partial x}(pS)-p\frac{\partial S}{\partial x}=0\]

soit:

(2.24)\[S\frac{\partial\rho U}{\partial t}+\frac{\partial}{\partial x}(\rho U^{2}S)+S\frac{\partial p}{\partial x}=0\]

Enfin l’équation de bilan de l’énergie, \(F(x)=H_{t}\overrightarrow{U}.\overrightarrow{n}\) qui s’annulle sur les parois et vaut \(-H_{t}U\) en \(S(x)\) et \(+H_{t}U\) en \(S(x+dx)\), ce qui donne au final:

\[\frac{\partial E_{t}}{\partial t}S\,dx+(H_{t}U)S(x+dx)-(H_{t}U)S(x)=0\]

soit à l’ordre 1 en x:

(2.25)\[S\frac{\partial E_{t}}{\partial t}+\frac{\partial}{\partial x}(H_{t}U\,S)=0\]

Les équations de bilan pour un gaz parfait dans une conduite de section \(S(x)\) s’écrivent donc:

(2.26)\[\begin{split}\begin{aligned} S\frac{\partial\rho}{\partial t}+\frac{\partial}{\partial x}(\rho US) & = & 0\\ S\frac{\partial\rho U}{\partial t}+\frac{\partial}{\partial x}(\rho U^{2}S)+S\frac{\partial p}{\partial x} & = & 0\\ S\frac{\partial E_{t}}{\partial t}+\frac{\partial}{\partial x}(H_{t}U\,S) & = & 0\end{aligned}\end{split}\]

avec l’équation d’état: \(H_{t}=E_{t}+p=\frac{\gamma}{\gamma-1}\,p+\frac{1}{2}\rho U^{2}\)

2.5.1. Écoulement stationnaire en conduite

Dans le cas d’un écoulement stationnaire, le système d’équations (2.23)- (2.25) se simplifie.

L’équation de bilan de la masse (2.23) s’écrit:

\[\rho US=cste\]

i.e. le débit massique (i.e. en kg/s) se conserve .

L’équation de bilan de l’énergie (2.25) s’écrit:

\[H_{t}US=cste\]

En notant \(h_{t}=\frac{H_{t}}{\rho}\) l’entalpie totale par unité de masse, on obtient:

\[h_{t}=cste\]

i.e. l’entalpie totale par unité de masse se conserve.

Pour l’équation de bilan de la quantité de mouvement (2.24), on obtient (en utilisant (2.23):

\[\begin{split}\begin{aligned} \frac{\partial}{\partial x}(\rho U^{2}S)+S\frac{\partial p}{\partial x} & = & \rho US\frac{\partial U}{\partial x}+U\frac{\partial}{\partial x}(\rho US)+S\frac{\partial p}{\partial x}\\ 0 & = & \rho US\frac{\partial U}{\partial x}+S\frac{\partial p}{\partial x}\end{aligned}\end{split}\]

ce qui se simplifie

\[\rho U\frac{\partial U}{\partial x}+\frac{\partial p}{\partial x}=0\]

Sous forme différentielle, on peut l’écrire: \(\rho U\,dU+dp=0\).

Le système d’équation pour un écoulement permanent en conduite s’écrit

(2.27)\[\begin{split}\begin{aligned} \rho US & = & cste\\ h_{t} & = & cste\\ \rho U\,dU+dp & = & 0\end{aligned}\end{split}\]

auquel on adjoint l’équation d’état \(h_{t}=\frac{\gamma}{\gamma-1}\frac{p}{\rho}+\frac{1}{2}U^{2}\)

Dans le cas où l’écoulement ne présente pas de discontinuité (choc), l’écoulement est aussi isentropique (exercice).

En prenant le logarithme de l’équation (2.27), on obtient:

\[\log\rho+\log U+\log S=cste\]

soit en différenciant:

\[\frac{d\rho}{\rho}+\frac{dU}{U}+\frac{dS}{S}=0\]

En utilisant l’équation (2.27) pour remplacer \(dU\), on a:

\[\frac{dS}{S}=-\frac{d\rho}{\rho}+\frac{dp}{\rho U^{2}}=\frac{dp}{\rho U^{2}}\left(1-\frac{U^{2}}{(\frac{dp}{d\rho})}\right)\]

En introduisant la célérité du son \(c=\sqrt{\frac{dp}{d\rho}}\), et le nombre de Mach local \(M=\frac{U}{c}\), l’équation précédente s’écrit:

(2.28)\[\frac{dS}{S}=\frac{dp}{\rho U^{2}}(1-M^{2})\]

Interprétons cette relation et ces conséquences si on veut accélérer un gaz:

• dans une conduite pour avoir une accélération de la vitesse \((dU>0)\) , il faut d’après (2.27) un gradient de pression négatif \((dp<0)\)

• si l’écoulement est subsonique \((M<1)\), la section de la conduite doit diminuer d’après (2.28)[ pour augmenter la vitesse, il faut donc un convergent \((dS<0)\)

• par contre si l’écoulement est supersonique \((M>1)\), la section de la conduite doit augmenter et il faut un divergent \((dS>0)\)

• C’est évidemment l’inverse si on veut décélérer le fluide

• l’écoulement ne peut devenir transsonique \((M=1)\) qu’au col \((dS=0)\) (Attention si \(dS=0\) on a pas forcement \(M=1\) )

On note ici une différence importante entre un écoulement subsonique et supersonique:

un convergent accélère un écoulement subsonique, mais décélère un écoulement supersonique.

2.5.2. Tuyère de Laval

Nous allons maintenant étudier le moyen de générer un écoulement supersonique à l’aide d’une tuyère convergente-divergente, dite tuyère de Laval. Ce dispositif est très utilisé pour étudier expérimentalement les écoulements supersoniques.

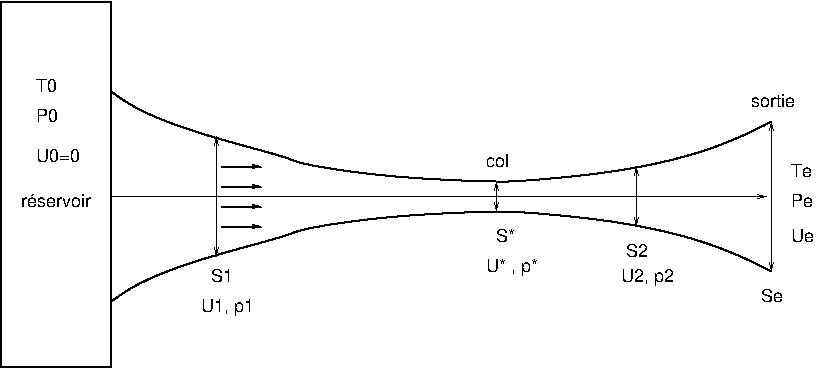
Fig. 2.42 écoulement en tuyère

On considère un réservoir, contenant un gaz à la pression \(p_{0}\) et à la température \(T_{0}\), relié à une sortie qui est à une pression \(p_{e}\) et une température \(T_{e}\) par une conduite convergente divergente de section \(S(x)\) , dont la valeur minimum vaut \(S^{*}\) au col.

Le réservoir est suffisamment grand pour considérer que la vitesse du fluide y est négligeable (\(U_{0}=0\)). Le fluide est quasiment au repos et donc dans des conditions d’arrêt: pression d’arrêt \(p_{0}\) et température d’arrêt \(T_{0}\).

En supposant que l’écoulement est stationnaire et isentropique dans la tuyère, les lois de bilan s’écrivent:

1. bilan d’énergie (ou premier principe de la thermodynamique):
   l’enthalpie totale \(h_{t}=h+\frac{1}{2}U^{2}\) se conserve et est égale à l’enthalpie d’arrêt \(h_{0}\)

   (2.29)\[h_{0}=h_{1}+\frac{1}{2}U_{1}^{2}=h_{2}+\frac{1}{2}U_{2}^{2}\]

2. conservation de l’entropie (ou second principe de la thermodynamique):

   \[s_{0}=s_{1}=s_{2}\]

3. conservation de la masse:
   le débit massique \(\dot{m}\) se conserve dans la tuyère

   \[\rho_{1}U_{1}S_{1}=\rho_{2}U_{2}S_{2}=\dot{m}=cste\]

4. bilan de quantité de mouvement (principe fondamental loi de Newton)

   \[(p_{1}+\rho_{1}U_{1}^{2})S_{1}+R=(p_{2}+\rho_{2}U_{2}^{2})S_{2}\]

   où \(R\) est la résultante des forces de pression sur la paroi entre les 2 sections:

   \[R=\int_{1}^{2}p.n_{x}\,dS\]

2.5.2.1. relations d’arrêt

Nous allons tout d’abord déterminer les relations entre l’état générateur (conditions d’arrêt) et l’état dans une section \(S_{1}\) quelconque de la conduite (en supposant un écoulement isentropique entre les deux).

La conservation de l’entalpie totale (2.29) permet d’obtenir une relation entre les températures, en notant que l’enthalpie pour un gaz parfait s’écrit \(h=C_{p}T\)

\[h_{0}=C_{p}T_{0}=C_{p}T_{1}+\frac{1}{2}U_{1}^{2}\]

soit

(2.30)\[\frac{T_{0}}{T_{1}}=1+\frac{U_{1}^{2}}{2C_{p}T_{1}}=1+\frac{(\gamma-1)U_{1}^{2}}{2c_{1}^{2}}=1+\frac{\gamma-1}{2}M_{1}^{2}\]

en introduisant la vitesse du son \(c_{1}^{2}=\gamma RT_{1}\) , la relation \(R=C_{p}-C_{v}\) et le nombre de Mach local \(M_{1}\).

En utilisant la relation isentropique \(\frac{p}{\rho^{\gamma}}=cste\) , qui s’écrit en fonction de \(T\): \(\frac{T}{\rho^{\gamma-1}}=cste\), on obtiens l’évolution de la masse volumique:

\[\frac{\rho_{1}}{\rho_{0}}=\left(\frac{T_{1}}{T_{0}}\right)^{\frac{1}{\gamma-1}}=\left(\frac{1}{1+\frac{\gamma-1}{2}M_{1}^{2}}\right)^{\frac{1}{\gamma-1}}\]

et l’évolution de la pression:

(2.31)\[\frac{p_{1}}{p_{0}}=\left(\frac{\rho_{1}}{\rho_{0}}\right)^{\gamma}=\left(\frac{1}{1+\frac{\gamma-1}{2}M_{1}^{2}}\right)^{\frac{\gamma}{\gamma-1}}\]

L’évolution de ces quantités est donnée sur la figure ci-dessous:

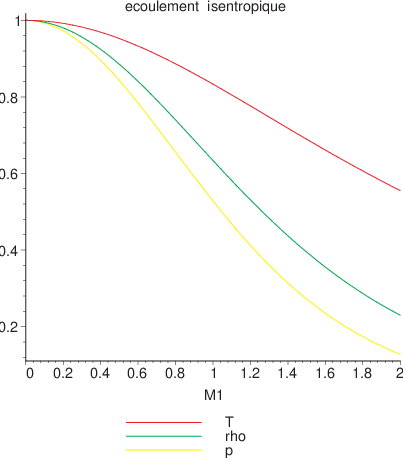
Fig. 2.43 relation d’arrêt

L’évolution de l’écoulement isentropique à partir de condition d’arrêt correspond donc à une diminution de la température, i.e. à la transformation de l’enthalpie (énergie interne + pression) en énergie cinétique. En effectuant un développement limité en nombre de Mach au voisinage de \(M_{1}=0\), on obtient les expressions suivantes:

\[\begin{split}\begin{aligned} \frac{T_{1}}{T_{0}} & = & 1-\frac{\gamma-1}{2}M_{1}^{2}\\ \frac{p_{1}}{p_{0}} & = & 1-\frac{\gamma}{2}M_{1}^{2}\\ \frac{\rho_{1}}{\rho_{0}} & = & 1-\frac{1}{2}M_{1}^{2}\end{aligned}\end{split}\]

On constate que les variations relatives à faible nombre de Mach sont proportionnelles à \(M_{1}^{2}\), et sont négligeables pour \(M_{1}<0.1\) (moins de \(1\%\)). A température ambiante \(c=360\,m/s\), un nombre de Mach \(M_{1}=0.1\) correspond donc à une vitesse de \(36\,m/s\) soit \(130\,km/h\). Cela justifie l’hypothèse d’écoulement incompressible \(\rho=cste\) pour des vitesses telles que \(M<0.1\).

ATTENTION: pour un écoulement incompressible, la masse volumique, la pression et la température sont constantes dans l’équation de bilan de masse et d’énergie (les fluctuations sont négligeables). Par contre dans l’équation de bilan de quantité de mouvement le terme en gradient de pression \(-\overrightarrow{grad}\,p\) doit être conservé, car il est du même ordre que le terme d’inertie \(\overrightarrow{U}.\overrightarrow{grad}\,\overrightarrow{U}\). Ce sont en effet les fluctuations de pression (dites fluctuations dynamiques) qui génèrent l’écoulement. Par contre ces fluctuations sont négligeables devant la pression totale (pression thermodynamique), ce qui permet de considérer les propriétés thermodynamiques d’un fluide incompressible comme constantes.

2.5.2.2. évolution du Mach dans une tuyère adaptée

Étudions l’évolution de la quantité de mouvement \(Q=\rho U\) dans la tuyère. Pour cela exprimons \(Q\) en fonction du nombre de Mach \(M\) , de \(p\) et de \(T\)

\[Q=\frac{p}{RT}M\sqrt{\gamma RT}=Mp\sqrt{\frac{\gamma}{RT}}\]

en remplaçant \(p\) et \(T\) en fonction des conditions d’arrêt (2.30)- (2.31)

\[Q=Mp_{0}\sqrt{\frac{\gamma}{RT_{0}}}\left(\frac{1}{1+\frac{\gamma-1}{2}M^{2}}\right)^{\frac{\gamma}{\gamma-1}}\left(1+\frac{\gamma-1}{2}M^{2}\right)^{\frac{1}{2}} \]

soit

\[Q=p_{0}\sqrt{\frac{\gamma}{RT_{0}}}\frac{M}{\left(1+\frac{\gamma-1}{2}M^{2}\right)^{\frac{\gamma+1}{2(\gamma-1)}}}\]

Si la tuyère est adaptée, l’écoulement est sonique au col \(S^{*}\), et la quantité de mouvement au col \(Q^{*}\) est obtenue en faisant \(M=1\) dans l’expression précédente

\[Q^{*}=p_{0}\sqrt{\frac{\gamma}{RT_{0}}}\left(\frac{2}{\gamma+1}\right)^{\frac{\gamma+1}{2(\gamma-1)}}\]

d’où le rapport \(\frac{Q^{*}}{Q}=\frac{S}{S^{*}}\) qui est aussi le rapport des sections d’après la conservation de la masse:

(2.32)\[\frac{Q^{*}}{Q}=\frac{S}{S^{*}}=\frac{1}{M}\left[\frac{2}{\gamma+1}\left(1+\frac{\gamma-1}{2}M^{2}\right)\right]^{\frac{\gamma+1}{2(\gamma-1)}}\]

Cette relation permet de définir l’évolution du nombre de Mach en fonction de la section de la tuyère.

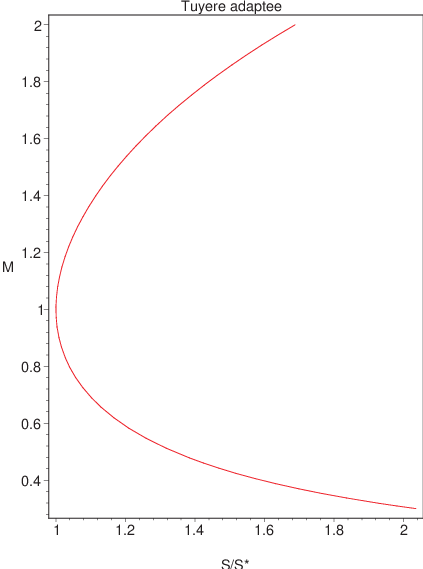
Fig. 2.44 évolution du nombre de Mach dans une tuyère

On constate que pour une section donnée, on a deux nombres de Mach possibles, un Mach supersonique ou un Mach subsonique. Donc pour une tuyère de Laval adaptée, on a 2 écoulements possibles. En effet dans la partie convergente, l’écoulement est forcément subsonique (puisqu’on part d’un écoulement au repos). Par contre dans la partie divergente, l’écoulement peut être soit subsonique, soit supersonique suivant la valeur de la pression en sortie de tuyère. En effet ayant la valeur du nombre de Mach, la relation (2.31) nous fournit la pression correspondante. Sur la figure ci-dessous on a tracé l’évolution des quantités \(M,p,T,\rho\) pour une tuyère parabolique et pour les 2 types d’écoulements possibles. D’après la relation de bilan de la quantité de mouvement (2.27), on déduit l’evolution de la vitesse en fonction de celle de la pression, puisque la vitesse augmente (\(du>0\)) lorsque la pression diminue dans la tuyère (\(dp>0\)).

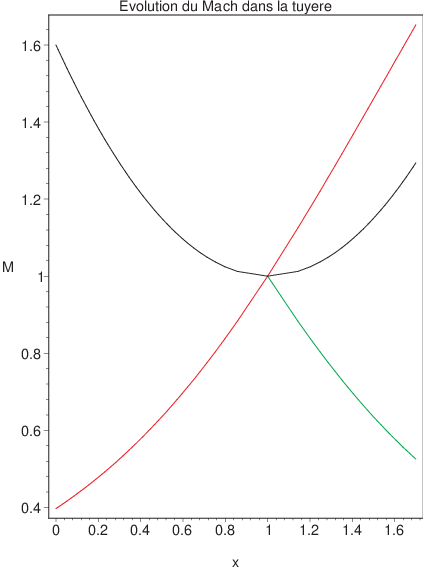
Fig. 2.45 évolution du Mach dans une tuyère

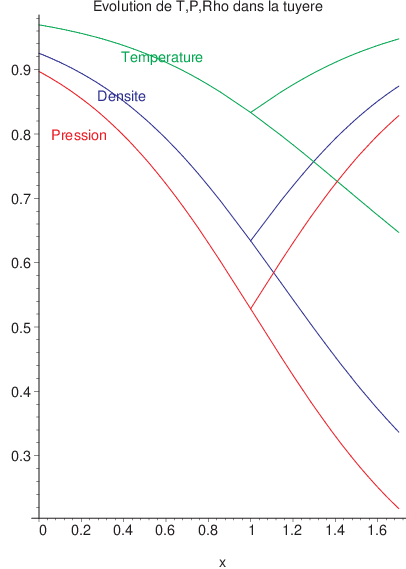
Fig. 2.46 évolution de pression, masse volumique et température dans une tuyère

On constate que si la pression de sortie (en \(S/S^{*}=1.29\) ,i.e. \(x=1.7\)) vaut \(Pe_{1}=0.83\,P_{0}\) l’écoulement reste subsonique dans la tuyère et sonique au col, par contre si la pression vaut \(Pe_{2}=0.22\,P_{0}\), alors l’écoulement est supersonique dans la partie divergente.

Si la pression en sortie \(Pe\) est supérieure à \(Pe_{1}\), alors l’écoulement n’est plus sonique au col et reste subsonique dans la tuyère.

Si la pression en sortie \(Pe\) est comprise entre \(Pe_{1}\) et \(Pe_{2}\) , alors l’écoulement n’est plus isentropique et on montrera que dans ce cas un choc se produit dans la tuyère.

Enfin si la pression en sortie est inférieure à \(Pe_{2}\) , alors en sortie l’écoulement n’est plus isentropique et un choc en sortie apparaît.