2. Approximation de couche limite

Fig. 2.23 écoulement autour d’une voiture DS citroen

A grand nombre de Reynolds, l’écoulement autour d’un obstacle peut se décomposer en plusieurs zones:

• loin des parois de l’obstacle, les effets visqueux sont négligeables (écoulement fluide parfait)

• proche des parois solides, dans une zone d’épaisseur \(\delta\) (couche limite)

• à l’arrière dans une zone de sillage (écoulement turbulent)

\(Ma\ll1\), \(Re\gg1\) mais stationnaire et laminaire, \(Fr\gg1\)

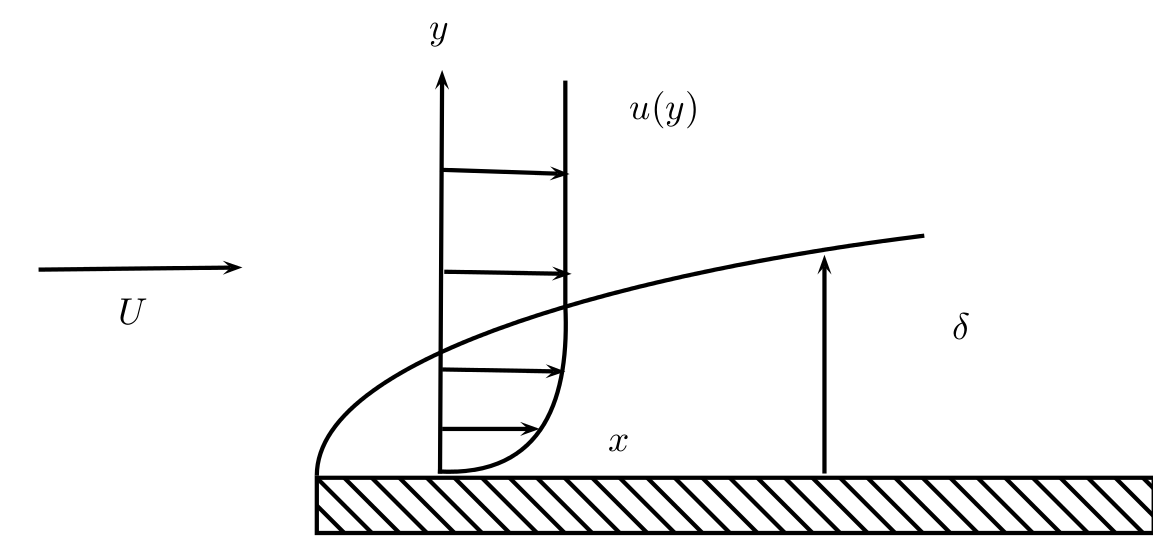
Fig. 2.24 écoulement de couche limite

Échelles de l’écoulement à une position \(x\) du bord d’attaque: \(x,\,\delta,\,U_{\infty},\,\rho,\,\mu\)

nombres sans dimension \(Re_{x}=\frac{\rho U_{\infty}x}{\mu}\gg1\) et \(\epsilon=\frac{\delta}{x}\ll1\)

• \(div\,\overrightarrow{U}=0\) donne l’ordre de grandeur de la vitesse \(V\) suivant y: \(V\approx\epsilon U_{\infty}\)

• A l’extérieure, l’écoulement est uniforme \(\Longrightarrow\) \(\frac{\partial p}{\partial x}=0\)
  dans la CL équilibre inertie = force visqueuse

  \[\rho u\frac{\partial u}{\partial x}\approx\mu\frac{\partial^{2}u}{\partial y^{2}}\,\Longrightarrow\epsilon=\frac{\delta}{x}\approx\frac{1}{\sqrt{Re_{x}}}\]

théorie de Prandtl (1875-1953) fondateur de l’aérodynamique

hypothèse: \(\epsilon=\delta/x=\theta(Re_{x}^{-1})\ll1\)

analyse en ordre de grandeur \(U_{0}\approx U_{\infty},\,V_{0}\approx\epsilon U_{\infty},\,x,\,\delta\approx\epsilon x,\,\epsilon^{2}\approx Re_{x}^{-1}\)

\[\underbrace{\frac{\partial u}{\partial x}}_{U_{0}/x}+\underbrace{\frac{\partial v}{\partial y}}_{V_{0}/\delta\approx U_{0}/x}=0\]

\[\underbrace{u\frac{\partial u}{\partial x}}_{U_{0}^{2}/x}+\underbrace{v\frac{\partial u}{\partial y}}_{U_{0}^{2}/x}=-\frac{1}{\rho}\frac{\partial p}{\partial x}+\underbrace{\nu\frac{\partial^{2}u}{\partial x^{2}}}_{\epsilon^{2}U_{0}^{2}/x}+\underbrace{\nu\frac{\partial^{2}u}{\partial y^{2}}}_{U_{0}^{2}/x}\]

\[\underbrace{u\frac{\partial v}{\partial x}}_{\epsilon U_{0}^{2}/x}+\underbrace{v\frac{\partial v}{\partial y}}_{\epsilon U_{0}^{2}/x}=-\frac{1}{\rho}\frac{\partial p}{\partial y}+\underbrace{\nu\frac{\partial^{2}v}{\partial x^{2}}}_{\epsilon^{3}U_{0}^{2}/x}+\underbrace{\nu\frac{\partial^{2}v}{\partial y^{2}}}_{\epsilon U_{0}^{2}/x}\]

\[\frac{\partial p}{\partial y}=0\,\Longrightarrow\,p=p(x)\]

gradient de pression externe \(\frac{1}{\rho}\frac{dp}{dx}=\pi(x)\) donné

\[\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0\]

\[u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=-\pi(x)+\nu\frac{\partial^{2}u}{\partial y^{2}}\]

système 2 inconnues \(u(x,y)\) et \(v(x,y)\): avec \(\psi(x,y)\) \(\leadsto\) une équation

Solution auto-similaire de Blasius (étudiant de Prandtl) pour \(\pi=0\)

\[\psi(x,y)=U_{0}\sigma(x)\,f(\eta) \mbox{ avec }\eta=\frac{y}{\sigma(x)}\mbox{ et }\sigma(x)=\sqrt{\frac{2\nu x}{U_{0}}}\]

\[u(x,y)=\frac{\partial\psi}{\partial y},\,v(x,y)=-\frac{\partial\psi}{\partial x}\mbox{ avec }\psi(x,y)=U_{0}\sigma(x)\,f(\eta)\]

le profil auto-similaire \(f(\eta)\) est solution de l’équation de Blasius:

\[f\,f''+2f'''=0\mbox{ avec }f(0)=0,f'(0)=0,f'(\infty)=1\]

développement de la couche limite (frottement \(C_{f}(x)\))

\[\delta\sim\sqrt{\frac{\mu x}{\rho U_{0}}},\,\,\,C_{f}=\frac{\tau_{w}}{\frac{1}{2}\rho U_{0}^{2}}=\frac{\mu\frac{\partial u}{\partial y}\mid_{w}}{\frac{1}{2}\rho U_{0}^{2}}\approx\frac{1}{\sqrt{Re_{x}}}\]

traînée sur une plaque plane de longueur \(L\), largueur \(b\) avec

\[F_{D}=\int_{0}^{L}\tau_{w}bdx\approx\rho U_{0}^{2}bL\left(\frac{\rho U_{0}L}{\mu}\right)^{-\frac{1}{2}}\]

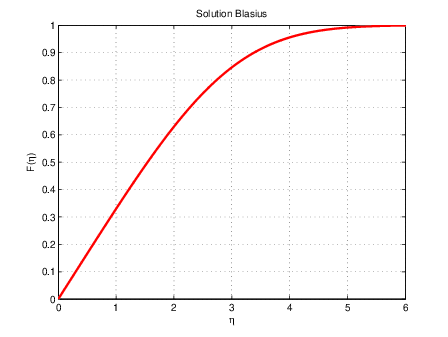
Fig. 2.25 solution de Blasius \(F(\eta)\)

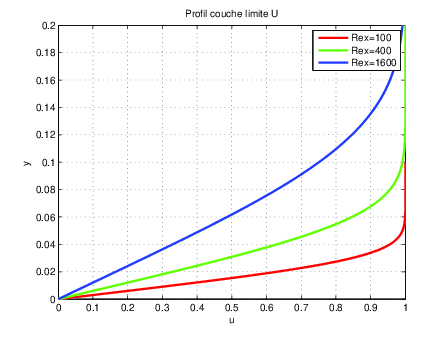
Fig. 2.26 profil de vitesse U horizontale

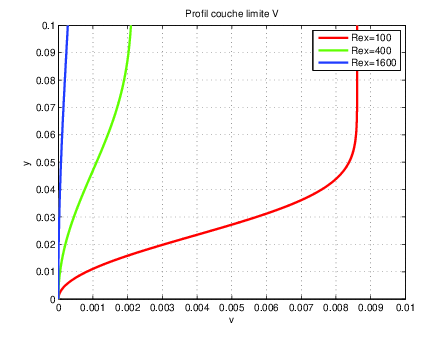
Fig. 2.27 profil de vitesse V verticale