2. Rappels de Mathématique

La description des écoulements en mécanique des fluides nécessite une maîtrise des outils mathématiques de base:

• vecteurs et opérateurs vectoriels en 2D et 3D

• fonctions scalaires et vectorielles de plusieurs variables (espace et temps)

• opérateurs différentielles et intégrales sur les fonctions

2.1. Vecteurs

2.1.1. vecteur en 2D

Soient \(\overrightarrow{A}\) et \(\overrightarrow{B}\) deux vecteurs de \(R^{2}\):

• composantes dans un repère cartésien de base \((\vec{e}_1,\vec{e}_2)\)

• \([A_{1},A_{2}]\) ou \(\{A_{i}\}_{i=1,2}\),

\[\overrightarrow{A}=A_1 \vec{e}_1+A_2 \vec{e}_2=\sum_{i=1}^2 A_i \vec{e}_i\]

• \([B_{1},B_{2}]\) ou \(\{B_{i}\}_{i=1,2}\)

\[\overrightarrow{B}=B_1 \vec{e}_1+B_2 \vec{e}_2=\sum_{i=1}^2 B_i \vec{e}_i\]

• produit scalaire: scalaire

  \[\overrightarrow{A}.\overrightarrow{B}=A_{1}B_{1}+A_{2}B_{2}=\sum_{i=1}^{2}\,A_{i}B_{i}\]

• norme euclidienne:

  \[\left\Vert \overrightarrow{A}\right\Vert =\sqrt{A_{1}^{2}+A_{2}^{2}}\]

• produit vectoriel: vecteur

  \[\overrightarrow{C}=\overrightarrow{A}\wedge\overrightarrow{B}\]

  perpendiculaire au plan d’amplitude \(A_{1}B_{2}-A_{2}B_{1}\)

• produit tensoriel: matrice

  \[\begin{split}\overline{\overline{M}}=\overrightarrow{A}\otimes\overrightarrow{B}=\left[\begin{array}{cc} A_{1}B_{1} & A_{1}B_{2}\\ A_{2}B_{1} & A_{2}B_{2} \end{array}\right]\end{split}\]

avec \(M_{ij}=A_{i}B_{j}\)

• les coordonnées cartésiennes d’un point M sont notées \(\left[x_{1},x_{2}\right]\) dans le repère \([O,\vec{e}_1,\vec{e}_2]\) :

\[ \overrightarrow{OM}= x_1 \vec{e}_1 + x_2 \vec{e}_2 \]

ou \(\left[x,y\right]\) dans le repère \([O,\overrightarrow{e_{x}},\overrightarrow{e_{y}}]\)

\[ \overrightarrow{OM}= x \overrightarrow{e_{x}} + y \overrightarrow{e_{y}} \]

2.1.2. vecteur en 3D

Soient \(\overrightarrow{A}\) et \(\overrightarrow{B}\) deux vecteurs de \(R^{3}\):

• composantes dans un repère cartésien : \(\{A_{i}\}_{i=1,3}\), \(\{B_{i}\}_{i=1,3}\)

• produit scalaire: scalaire

  \[\overrightarrow{A}.\overrightarrow{B}=\sum_{i=1}^{3}\,A_{i}B_{i}\]

• produit vectoriel: vecteur \(\overrightarrow{C}=\overrightarrow{A}\wedge\overrightarrow{B}\) avec

  \[\overrightarrow{C}=\left[\begin{array}{ccc} A_{2}B_{3}-A_{3}B_{2}, & A_{3}B_{1}-A_{1}B_{3}, & A_{1}B_{2}-A_{2}B_{1}\end{array}\right]\]

• produit tensoriel: matrice \(\overline{\overline{M}}=\overrightarrow{A}\otimes\overrightarrow{B}\) avec \(M_{ij}=A_{i}B_{j}\)

• on note \(\left[x_{1},x_{2},x_{3}\right]\) les coordonnées cartésiennes d’un point dans le repère \([O,\overrightarrow{e_{1}},\overrightarrow{e_{2}},\overrightarrow{e_{3}}]\),

\[ \overrightarrow{OM} = x_1 \vec{e}_1 + x_2 \vec{e}_2 + x_3 \vec{e}_3\]

ou \(\left[x,y,z\right]\) dans le repère \([O,\overrightarrow{e_{x}},\overrightarrow{e_{y}},\overrightarrow{e_{z}}]\)

\[ \overrightarrow{OM} = x \vec{e}_x + y \vec{e}_y + z \vec{e}_z\]

2.2. Fonctions de plusieurs variables

2.2.1. fonction scalaire f(x,t) d’une variable d’espace x et du temps t

exemple: \(f(x,t)=x^2e^{-t}\)

• dérivée partielle en temps:

(2.1)\[\begin{eqnarray} \frac{\partial f}{\partial t} &=&\lim_{dt \to 0} \frac{f(x,t+dt)-f(x,t)}{dt}\\ &=& -tx^2e^{-t} \end{eqnarray}\]

• dérivée partielle en espace:

(2.2)\[\begin{eqnarray} \frac{\partial f}{\partial x}&=&\lim_{dx \to 0} \frac{f(x+dx,t)-f(x,t)}{dx}\\ &=& 2xe^{-t} \end{eqnarray}\]

• sa différentielle est un scalaire:

(2.3)\[\begin{eqnarray} df &=&\frac{\partial f}{\partial x}dx+\frac{\partial f}{\partial t}dt\\ &=& 2xe^{-t}\;dx- tx^2e^{-t}\;dt \end{eqnarray}\]

2.2.2. fonction scalaire f(x,y,t) de 2 variables d’espace x,y et du temps t

exemple: \(f(x,y,t)=x^2ye^{-t}\)

• sa différentielle est un scalaire:

(2.4)\[\begin{eqnarray} df&=&\frac{\partial f}{\partial x}dx+\frac{\partial f}{\partial y}dy+\frac{\partial f}{\partial t}dt\\ &=& 2xye^{-t} dx + x^2e^{-t}dy - x^2ye^{-t}dt \end{eqnarray}\]

• son gradient (par rapport aux variables spatiales) est un vecteur de composantes \([\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}]\)

(2.5)\[\begin{eqnarray} \overrightarrow{grad}\;f&=&\overrightarrow{\nabla}f\,=\,\frac{\partial f}{\partial x}\overrightarrow{e_{x}}+\frac{\partial f}{\partial y}\overrightarrow{e_{y}}\\ &=& \begin{bmatrix} 2xye^{-t} \\ x^2e^{-t}\end{bmatrix} \end{eqnarray}\]

Note

A un instant t fixé, c’est un vecteur perpendiculaire aux courbes iso-valeurs \(f(x,y)=cste\), qui indique la direction où la fonction \(f\) croît.

• on note \(\overrightarrow{grad}=\overrightarrow{\nabla}\) le vecteur opérateur gradient:

  \[\overrightarrow{\nabla}=\left[\begin{array}{ccc} \frac{\partial}{\partial x} & \frac{\partial}{\partial y}\end{array}\right]=\left[\begin{array}{ccc} \frac{\partial}{\partial x_{1}} & \frac{\partial}{\partial x_{2}}\end{array}\right]\]

2.2.3. fonction scalaire f(x,y,z,t) de 3 variables d’espace et du temps

exemple: \(f(x,y,z,t)=x^2yze^{-t}\)

• sa différentielle est un scalaire:

(2.6)\[\begin{eqnarray} df&=&\frac{\partial f}{\partial x}dx+\frac{\partial f}{\partial y}dy+\frac{\partial f}{\partial z}dz+\frac{\partial f}{\partial t}dt\\ &=& 2xyze^{-t} dx + x^2ze^{-t}dy + x^2ye^{-t}dz - x^2yze^{-t}dt \end{eqnarray}\]

• son gradient (par rapport aux variables spatiales) est un vecteur:

(2.7)\[\begin{eqnarray} \overrightarrow{grad}f&=&\overrightarrow{\nabla}f\,=\,\frac{\partial f}{\partial x}\overrightarrow{e_{x}}+\frac{\partial f}{\partial y}\overrightarrow{e_{y}}+\frac{\partial f}{\partial z}\overrightarrow{e_{z}}\\ &=& \begin{bmatrix} 2xyze^{-t} \\ x^2z e^{t} \\ x^2y e^{t}\end{bmatrix} \end{eqnarray}\]

2.2.4. fonction vectorielle \(\overrightarrow{U}(x,y,t)\) en 2D

c’est une fonction vectorielle de composantes \(\{u(x,y,t),\,v(x,y,t)\}\)

exemple: \(\overrightarrow{U}(x,y,t)=\begin{bmatrix} 2xye^{-t} \\ (x^{2}+y^{2})e^{t}\end{bmatrix}\)

• sa matrice Jacobienne est la matrice des gradients:

(2.8)\[\begin{eqnarray} J&=&\left[\begin{array}{cc} \frac{\partial u}{\partial x} & \frac{\partial u}{\partial y}\\ \frac{\partial v}{\partial x} & \frac{\partial v}{\partial y} \end{array}\right]=\left[\frac{\partial u_{i}}{\partial x_{j}}\right]\\ &=& \begin{bmatrix} 2ye^{-t} & 2x e^{-t} \\ 2xe^{t} & 2y e^{t} \end{bmatrix} \end{eqnarray}\]

• sa divergence est un scalaire:

(2.9)\[\begin{eqnarray} div\,\overrightarrow{U}&=&\overrightarrow{\nabla}.\overrightarrow{U}=\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\\ &=& 2ye^{-t} + 2ye^{t} \end{eqnarray}\]

C’est la trace de la matrice jacobienne \(J\).

Note

La divergence traduit la compression ou l’expansion du champs

• son rotationnel est un vecteur perpendiculaire au plan et d’amplitude:\(\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}\)

(2.10)\[\begin{eqnarray} \overrightarrow{rot}\,\overrightarrow{U}=\overrightarrow{\nabla}\wedge\overrightarrow{U}=\left\{ \frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}\right\} \overrightarrow{e_{z}} \end{eqnarray}\]

Note

Le rotationnel traduit la rotation solide du champ

• l’opérateur de transport: \(\overrightarrow{U}.\overrightarrow{grad}()=u\frac{\partial}{\partial x}+v\frac{\partial}{\partial y}\)

  traduit le transport par le champ d’une quantité \(F(x,y)\), i.e. sa variation \(dF\) le long d’une trajectoire à partir du point M de coordonnées \([x,y]\):

  \[dF = F(M')-F(M)=\overrightarrow{U}.\overrightarrow{grad}(F)\,dt\,\,\,\mbox{{\, avec\,}}\,\,\overrightarrow{MM'}=\overrightarrow{dM}=\overrightarrow{U}dt\]

  • appliquée à un champ scalaire \(f\) on obtient le scalaire:

  \[\overrightarrow{U}.\overrightarrow{grad}f=u\frac{\partial f}{\partial x}+v\frac{\partial f}{\partial y}\]

  • appliqué à un champ de vecteur \(\overrightarrow{U}\), on obtiens le vecteur

  \[\begin{split}\overrightarrow{U}.\overrightarrow{grad}\overrightarrow{U}=\left[\begin{array}{c} u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}\\ u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y} \end{array}\right]\end{split}\]

2.2.5. fonction vectorielle \(\overrightarrow{U}(x,y,z,t)\) en 3D

c’est une fonction vectorielle de composantes \(\{u(x,y,z,t),\,v(x,y,z,t),\,w(x,y,z,t)\}\)

• sa divergence est un scalaire:

  \[div\,\overrightarrow{U}=\overrightarrow{\nabla}.\overrightarrow{U}=\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}\]

• son rotationnel est un vecteur:

  \[\overrightarrow{rot}\,\overrightarrow{U}=\overrightarrow{\nabla}\wedge\overrightarrow{U}=\left\{ \frac{\partial w}{\partial y}-\frac{\partial v}{\partial z}\right\} \overrightarrow{e_{x}}+\left\{ \frac{\partial u}{\partial z}-\frac{\partial w}{\partial x}\right\} \overrightarrow{e_{y}}+\left\{ \frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}\right\} \overrightarrow{e_{z}}\]

• l’opérateur de transport \(\overrightarrow{U}.\overrightarrow{grad}()=u\frac{\partial}{\partial x}+v\frac{\partial}{\partial y}+w\frac{\partial}{\partial z}\)\

  • appliqué à un scalaire donne le scalaire

  \[\overrightarrow{U}.\overrightarrow{grad}f=u\frac{\partial f}{\partial x}+v\frac{\partial f}{\partial y}+w\frac{\partial f}{\partial z}\]

  • appliqué à un vecteur donne le vecteur

  \[\begin{split}\overrightarrow{U}.\overrightarrow{grad}\overrightarrow{U}=\left[\begin{array}{c} u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+w\frac{\partial u}{\partial z}\\ u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}+w\frac{\partial v}{\partial z}\\ u\frac{\partial w}{\partial x}+v\frac{\partial w}{\partial y}+w\frac{\partial w}{\partial z} \end{array}\right]\end{split}\]

2.3. opérateurs gradient, divergence, et rotationnelle

Notons enfin quelques propriétés de ces opérateurs:

\[div(\overrightarrow{grad}\,f)=\Delta f=\frac{\partial^{2}f}{\partial x^{2}}+\frac{\partial^{2}f}{\partial y^{2}}+\frac{\partial^{2}f}{\partial z^{2}}\]

\[\overrightarrow{rot}(\overrightarrow{grad}\,f)=0\]

\[div(f\overrightarrow{U})=\overrightarrow{U}.\overrightarrow{grad}\,f\,+f\,div\overrightarrow{U}\]

\[\overrightarrow{grad}(\frac{1}{2}U^{2})=\overrightarrow{U}\wedge\overrightarrow{rot}\,\overrightarrow{U}+\overrightarrow{U}.\overrightarrow{grad}\,\overrightarrow{U}\]

2.3.1. Théorème de la divergence:

• soit \(\Omega\) un domaine fermé de frontière \(\Gamma\) :

  le bilan des flux à travers la surface \(\Gamma\) est égale à la divergence du champ de vitesse dans le domaine, soit

  \[\int_{\Omega}div(\overrightarrow{U})\,d\Omega=\int_{\Gamma}\overrightarrow{U}.\overrightarrow{n}\,ds\]

• Pour un domaine carré \(\Omega=[0,a]x[0,a]\) de coté \(a\), cela correspond à une intégration suivant les axes:

(2.11)\[\begin{eqnarray} \int_{0}^{a}\int_{0}^{a}(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y})\,dxdy & = & \int_{0}^{a}dy\int_{0}^{a}(\frac{\partial u}{\partial x})\,dx+\int_{0}^{a}dx\int_{0}^{a}(\frac{\partial v}{\partial y})\,dy\\ & = & \int_{0}^{a}(u(a,y)-u(0,y))dy+\int_{0}^{a}(v(x,a)-v(x,a))dx\\ & = & \int_{\Gamma_{x=a}}\overrightarrow{U}.\overrightarrow{n}\,ds+\int_{\Gamma_{x=0}}\overrightarrow{U}.\overrightarrow{n}\,ds\\ & + & \int_{\Gamma_{y=a}}\overrightarrow{U}.\overrightarrow{n}\,ds+\int_{\Gamma_{y=0}}\overrightarrow{U}.\overrightarrow{n}\,ds \end{eqnarray}\]

• On généralise facilement au cas du flux \(f\,\overrightarrow{U}\) d’un scalaire \(f\)

\[\int_{\Omega}div(f\,\overrightarrow{U})\,d\Omega=\int_{\Gamma}f\,\overrightarrow{U}.\overrightarrow{n}\,ds\]

2.4. Développement limitée (série de Taylor):

2.4.1. fonction d’une variable d’espace x et du temps t

• développement limité en temps

  \[f(x,t+dt)=f(x,t)+\frac{\partial f}{\partial t}dt+\frac{1}{2}\frac{\partial^{2}f}{\partial t^{2}}(dt)^{2}+\theta(dt^{2})\]

• développement limité en espace

  \[f(x+dx,t)=f(x,t)+\frac{\partial f}{\partial x}dx+\frac{1}{2}\frac{\partial^{2}f}{\partial x^{2}}(dx)^{2}+\theta(dx^{2})\]

• développement limité en temps et en espace:

  \[f(x+dx,t+dt)=f(x,t)+\frac{\partial f}{\partial x}dx+\frac{\partial f}{\partial t}dt+\frac{1}{2}\frac{\partial^{2}f}{\partial x^{2}}dx^{2}+\frac{\partial^{2}f}{\partial x\partial t}dxdt+\frac{1}{2}\frac{\partial^{2}f}{\partial t^{2}}dt^{2}+\theta(dx^{2},dt^{2})\]

2.5. Fluides

Un fluide, bien que constitué d’atomes au niveau microscopique, peut être considéré au niveau macroscopique comme un milieu continu: c’est à dire que les propriétés du fluide sont des fonctions continues des variables d’espace \((x,y,z)\) et du temps \(t\).

Décrire le mouvement d’un fluide fait appel à des notions différentes de celles développées en Mécanique du point ou du solide. Le fluide est en mouvement continue et on parle donc d’écoulement de fluide. Contrairement au solide, on s’intéresse donc plus à la vitesse des particules fluides qu’à leur déplacement ou déformation comme en mécanique des solides.

2.6. particule fluide

Pour décrire un fluide, on introduit la notion de « particule fluide ». On isole (par la pensée ou en trouvant un moyen de visualisation, coloration par exemple) des parties restreintes du fluide, appelée « particules fluide ». Ces « particules fluides » contiennent statistiquement le même nombre de molécules et doivent avoir un volume \(V=a^{3}\) dont la dimension \(a\) vérifie les hypothèses de milieu continue:

1. \(a\) est très petite devant les échelles caractéristiques \(L\) de l’écoulement (diamêtre du canal, taille de l’obstacle,..).

2. \(a\) est très grand devant le libre parcours moyen \(l\) des molécules (échelle microscopique).

Ainsi pour de l’hélium à pression et température standard, le libre parcours moyen vaut:

\[l\approx2,6\,10^{-6}\,m\]

et dans un volume molaire \(\mathcal{V}\) :

\[\mathcal{V}\approx22\,10^{-3}\,m^{3}\]

il y a \(\mathcal{N}=6,02\,10^{23}\) atomes d’hélium. Donc une particule fluide de taille \(a=0.1\,mm\,\gg l\), contient \(n\approx30\,10^{12}\) atomes.

Pour une particule fluide, on peut alors définir:

1. sa masse \(m\) (somme des masses des molécules),

2. son volume \(V\),

3. sa vitesse \(\overrightarrow{U}\) (vitesse moyenne des molécules),

4. sa température \(T\) (qui mesure l’agitation moléculaire),

5. sa pression \(p\) ( échange de quantité de mouvement des molécules à travers la surface de la particule fluide).

On peut ensuite en déduire pour la particule:

1. la masse volumique \(\rho=\frac{m}{V}\)

2. la quantité de mouvement \(m\overrightarrow{U}\)

3. la quantité de mouvement par unité de volume \(\rho\overrightarrow{U}\)

4. l’énergie interne \(E\)

5. l’énergie interne par unité de masse \(e=\frac{E}{m}\)

6. l’énergie interne par unité de volume \(\rho e\)

Note

remarque

on utilise aussi par abus de langage, le terme densité pour masse volumique. ce n’est pas exacte, car la densité est par définition un nombre sans dimension, qui est le rapport entre la masse volumique \(\rho\) et la masse volumique de l’eau pure \(\rho_{0}=1000\,kg\,m^{-3}\) à \(3,98\,\)C

2.7. description lagrangienne

On peut, de manière analogue à ce que l’on fait en Mécanique du solide, isoler (par la pensée ou en trouvant un moyen de visualisation, coloration par exemple) une partie restreinte du fluide appelée particule fluide et la suivre au cours du temps c’est à dire connaître à chaque instant sa position.

Soit \(M(t)\) la position de la particule à l’instant \(t\), de coordonnées \(\{x_{M}(t),y_{M}(t),z_{M}(t)\}\), la vitesse de la particule aura pour composantes:

\[u_{M}=\frac{dx_{M}}{dt}\,,\,v_{M}=\frac{dy_{M}}{dt}\,,\,w_{M}=\frac{dz_{M}}{dt}\]

Au cours du temps, la particule sera en différents points M , l’ensemble des points M constitue la trajectoire de la particule. Cette façon de faire est appelée méthode de Lagrange, les variables introduites sont appelées variables de Lagrange. Elle s’avère dans la plupart des cas délicate car il n’est pas facile de suivre toutes les particules qui peuvent rentrer et sortir du domaine.

2.8. description eulérienne

La méthode d’Euler consiste à connaître la vitesse des particules au cours du temps t à un endroit donné déterminé par ses coordonnées, par exemple cartésiennes \((x,y,z)\). Elle est plus employée que la méthode de Lagrange, la connaissance du champ des vitesses étant suffisante pour la description du fluide en mouvement.

On choisit un petit élément de volume \(dxdydz\), dont la position \((x,y,z)\) est fixe dans le référentiel de l’observateur, et on détermine la vitesse des particules fluides qui traversent cet élément de volume. La vitesse \(\overrightarrow{U}\) mesurée dépend évidemment du temps \(t\) et du point de mesure \((x,y,z)\):

\[\overrightarrow{U}=\{u(x,y,z,t),\,v(x,y,z,t),\,w(x,y,z,t)\}\]

De façon générale, les propriétés du fluide mesurées par la méthode d’Euler dépendent donc du point \((x,y,z)\) et du temps \(t\).

Si l’on compare les fluides avec les solides, la première remarque qui s’impose concerne l’isotropie (les propriétés sont les mêmes dans toutes les directions spatiales) des fluides usuels qui est toujours réalisée (si l’on agit pas sur le fluide en tout cas!).

En particulier, en un point quelconque d’un fluide, la pression est indépendante de la direction de la normale à la surface élémentaire sur laquelle elle s’exerce (théorème de Pascal).

2.9. propriétés d’un écoulement

2.9.1. écoulement stationnaire

L’écoulement du fluide est permanent ou stationnaire si ses composantes de vitesse sont indépendantes de la variable temps t ; il est dit non-permanent ou instationnaire si cette condition n’est pas réalisée.

Astuce

le lecteur s’évitera de conclure que, dans un écoulement permanent, la particule fluide n’a pas d’accélération, car ceci est en général faux ! Dans un écoulement stationnaire, la vitesse en un point est indépendante du temps, mais elle peut varier d’un point à un autre, et donc les particules fluides peuvent être soumise à une accélération

2.9.2. écoulement uniforme

L’écoulement du fluide est uniforme si ses composantes de vitesse sont indépendantes des coordonnées d’espace; il est non-uniforme si cette condition n’est pas remplie.

Astuce

le lecteur s’évitera de conclure que, dans un écoulement uniforme, la particule fluide n’a pas d’accélération.

2.9.3. ligne de courant

On appelle ligne de courant , à un instant t fixé, une courbe dont la direction tangente en chacun de ses points est la direction du vecteur vitesse. L’équation d’une ligne de courant se calcule par intégration, à un instant t fixé, des équations suivantes (en notant \(dx,dy,dz\) la tangente en \((x,y,z)\) à la ligne de courant):

\[\frac{dx}{u(x,y,z,t)}=\frac{dy}{v(x,y,z,t)}=\frac{dz}{w(x,y,z,t)}\]

Astuce

les lignes de courants et les trajectoires sont des courbes distinctes, sauf pour les écoulements stationnaires.

2.9.4. écoulement plan

Si la vitesse n’a pas de composante suivant \(z\), l’écoulement est plan ou bi-dimensionnel. Les particules fluides restent dans le plan, et la vitesse ne dépend en général que de \((x,y)\) et du temps \(t\).

2.9.5. écoulement unidimensionnel

Si la vitesse a une seule composante de vitesse \(u(x,t)\), l’écoulement est 1D. Les trajectoires et les lignes de courant sont des droites.

2.10. Cinématique des fluides

2.10.1. dérivation suivant la méthode d’Euler

Considérons la fonction scalaire \(f(x,y,z,t)\) rendant compte d’une grandeur physique caractéristique du fluide au point de coordonnées \((x,y,z)\) et au temps t. La particule fluide au temps \(t+dt\) sera au point de coordonnées \(x+u\,dt,\,\,y+v\,dt,\,\,z+w\,dt\). La variation de la fonction \(f\) sera donc égale à :

\[\begin{split}\begin{aligned} df & = & f(x+u\,dt,\,\,y+v\,dt,\,\,z+w\,dt,t+dt)-f(x,y,z,t)\\ & = & \frac{\partial f}{\partial t}dt+\frac{\partial f}{\partial x}u\,dt+\frac{\partial f}{\partial y}v\,dt+\frac{\partial f}{\partial z}w\,dt+\theta(dt^{2})\end{aligned}\end{split}\]

La dérivée \(\frac{df}{dt}\), que l’on note \(\frac{Df}{Dt}\) et que l’on appelle dérivée particulaire, est égale à :

\[\frac{Df}{Dt}=\frac{\partial f}{\partial t}+u\frac{\partial f}{\partial x}+v\frac{\partial f}{\partial y}+w\frac{\partial f}{\partial z}=\frac{\partial f}{\partial t}+\overrightarrow{U}.\overrightarrow{grad}\,f=\frac{\partial f}{\partial t}+\overrightarrow{U}.\overrightarrow{\nabla}f\]

2.10.2. cinématique

Au cours du mouvement, une particule de fluide subit des changements de position, d’orientation et de forme. Nous considérons deux points voisins \(M(x,y,z\)) et \(M'(x+dx,y+dy,z+dz)\) d’un même fluide. Leurs vitesses respectives \(\overrightarrow{U}(M)\) et \(\overrightarrow{U}(M')\) s’écrivent à un instant \(t\) donné (en utilisant des développements limités):

\[\begin{split}\begin{aligned} u_{M'} & = & u(x+dx,y+dy,z+dz,t)=u_{M}+\frac{\partial u}{\partial x}dx+\frac{\partial u}{\partial y}dy+\frac{\partial u}{\partial z}dz\\ v_{M'} & = & v(x+dx,y+dy,z+dz,t)=v_{M}+\frac{\partial v}{\partial x}dx+\frac{\partial v}{\partial y}dy+\frac{\partial v}{\partial z}dz\\ w_{M'} & = & w(x+dx,y+dy,z+dz,t)=w_{M}+\frac{\partial w}{\partial x}dx+\frac{\partial w}{\partial y}dy+\frac{\partial w}{\partial z}dz\end{aligned}\end{split}\]

Ces expressions s’écrivent sous forme matricielle:

\[\overrightarrow{U}_{M'}=\overrightarrow{U}_{M}+\overline{\overline{grad}}(\overrightarrow{U})\,\overrightarrow{MM'}\]

En décomposant la matrice des gradients de vitesse \(\overline{\overline{grad}}(\overrightarrow{U})\) en sa partie symétrique et anti-symétrique, ces relations peuvent se réécrire sous la forme suivante :

\[\begin{split}\begin{aligned} u_{M'} & = & u_{M}+\frac{1}{2}\left((\frac{\partial u}{\partial z}-\frac{\partial w}{\partial x})dz-(\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y})dy\right)+d_{1}\\ d_{1} & = & +\frac{1}{2}\left(2\frac{\partial u}{\partial x}dx+(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x})dy+(\frac{\partial u}{\partial z}+\frac{\partial w}{\partial x})dz\right)\\ v_{M'} & = & v_{M}+\frac{1}{2}\left((\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y})dx-(\frac{\partial w}{\partial y}-\frac{\partial v}{\partial z})dz\right)+d_{2}\\ d_{2} & = & +\frac{1}{2}\left((\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x})dx+2\frac{\partial v}{\partial y}dy+(\frac{\partial v}{\partial z}+\frac{\partial w}{\partial y})dz\right)\\ u_{M'} & = & u_{M}+\frac{1}{2}\left((\frac{\partial w}{\partial y}-\frac{\partial v}{\partial z})dy-(\frac{\partial u}{\partial z}-\frac{\partial w}{\partial x})dx\right)+d_{3}\\ d_{3} & = & +\frac{1}{2}\left((\frac{\partial w}{\partial x}+\frac{\partial u}{\partial z})dx+(\frac{\partial w}{\partial y}+\frac{\partial v}{\partial z})dy+2\frac{\partial w}{\partial z}dz\right)\end{aligned}\end{split}\]

soit sous forme vectorielle:

\[\overrightarrow{U}_{M'}=\underbrace{\overrightarrow{U}_{M}}_{\mbox{{translation}}}+\underbrace{\overrightarrow{\Omega}\wedge\overrightarrow{MM'}}_{\mbox{{rotation}}}+\underbrace{\overrightarrow{D}}_{\mbox{{déformation}}}\]

où \(\overrightarrow{\Omega}=\frac{1}{2}\overrightarrow{rot}\,\overrightarrow{U}\) est le vecteur tourbillon instantané et \(\overrightarrow{D}\) la vitesse de déformation instantanée.

Note

D’une manière générale, le mouvement d’une particule fluide est la superposition d’une translation, d’une rotation et d’une déformation.

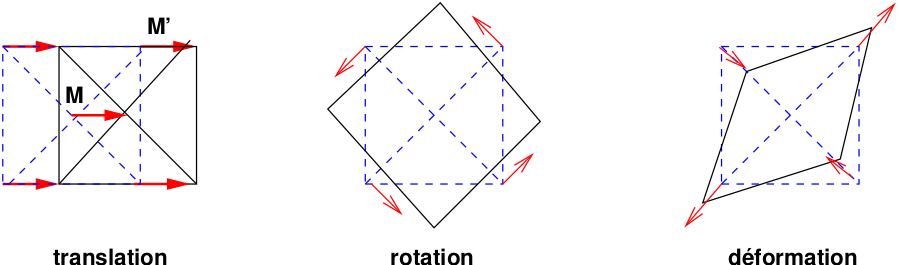
Fig. 2.15 mouvement et déformation d’une particule fluide

Pour un champ de vitesse à l’origine \(U(0,0)=[2,2]\) avec un gradient suivant:

\[\begin{split}\overrightarrow{grad}\,U=\left(\begin{array}{cc} 2 & 1\\ -1 & -1 \end{array}\right)\end{split}\]

on détermine la trajectoire et la déformation de la particule fluide:

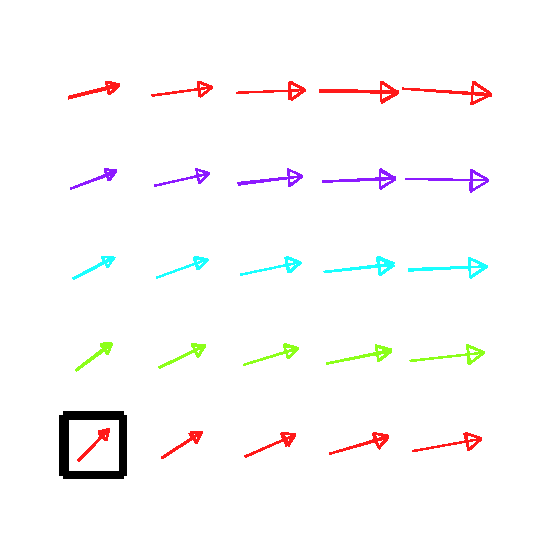
Fig. 2.16 Champ de vitesse et position initiale d’une particule fluide

La vidéo suivante montre la trajectoire et la déformation de cette particule fluide: