4. Écoulement à surface libre

objectifs: appréhender les domaines de l’hydraulique, hydrodynamique maritime et la notion d’ondes de surface

Fig. 4.3 crue de rivière

Fig. 4.4 tsunami au japon

4.1. Modèle en eau peu profonde (rivière)

fluide incompressible (eau), effet de gravité, surface libre, faible profondeur

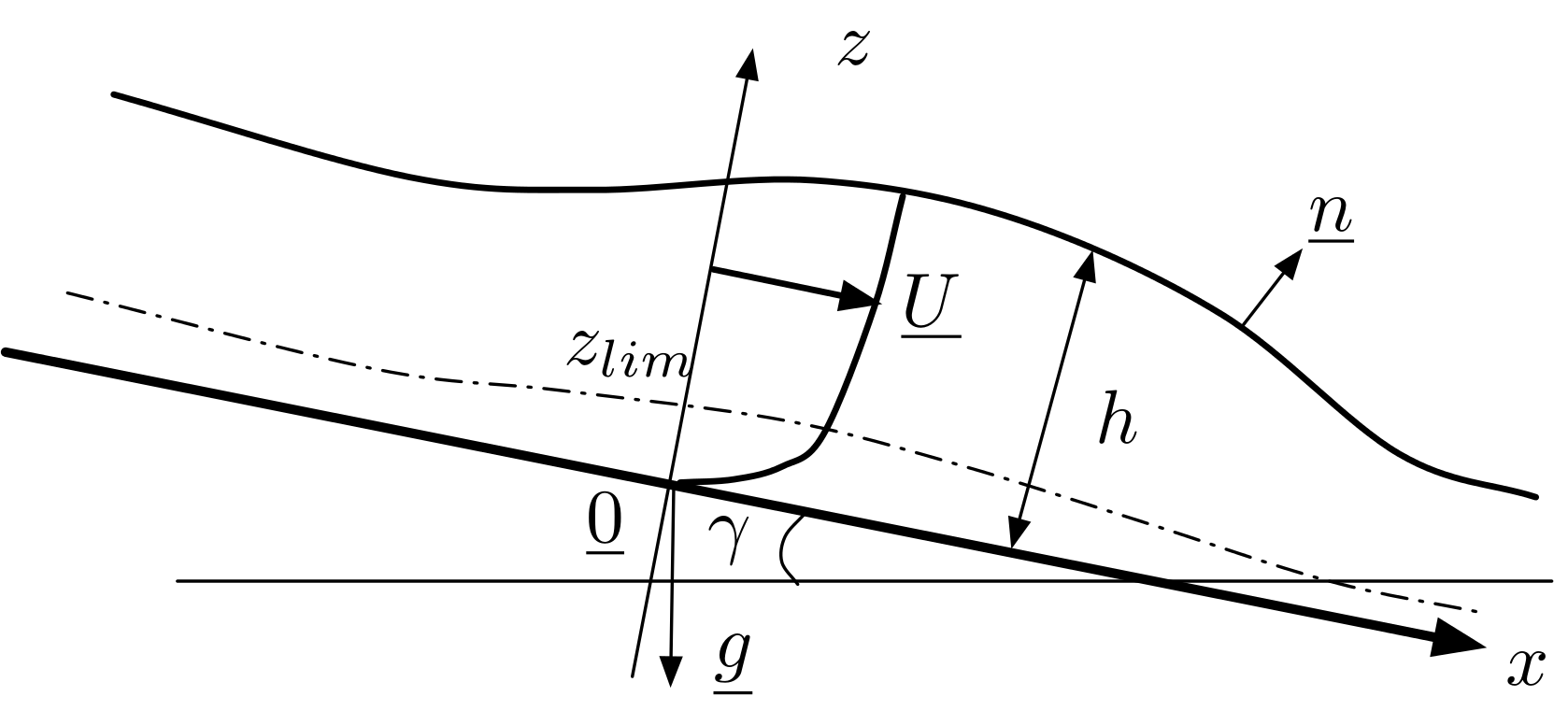
Fig. 4.5 modèle en eau peu profonde

Équations de Navier-Stokes en 2D \(\overrightarrow{U}=(u,v)\)

\[\begin{split}\begin{aligned} div(\overrightarrow{U}) & =0\\ \frac{\partial\rho\overrightarrow{U}}{\partial t}+div\left(\rho\overrightarrow{U}\otimes\overrightarrow{U}\right) & =-\overrightarrow{\nabla}p+\rho\overrightarrow{g}+\mu\Delta\overrightarrow{U}\end{aligned}\end{split}\]

paramétres: \(U_{0}\), \(L\) , \(\tau_{0}\) \(h\), \(g\), \(\gamma\), \(\mu\), \(\rho\)

5 nombres sans dimension

\[Re=\frac{\rho U_{0}h}{\mu},\,\,Fr=\frac{U_{0}}{\sqrt{gh}},\,\,\gamma,\,\,\epsilon=\frac{h}{L},\,St=\frac{U_{0}\tau_{0}}{L}\]

l’échelle de vitesse suivant \(z\) est petite : \(W_{0}\approx\epsilon U_{0}\)

exemple:

\(\mu=10^{-3}\,Pa\,s\), \(\rho=10^{3}\,kg/m^{3}\), \(U_{0}=1-10m/s\) , \(h\sim1\,m\), \(L\approx km\)

\[Re\sim10^{6}-10^{7},\,\,Fr\sim0.3-3\]

hypothèses:

• quantités moyennes

• répartition de pression hydro-statique en \(z\) avec \(p=P_{0}\) à la surface

\[p=P_{0}+\rho g\cos(\gamma)(h-z)\]

• frottement \(\tau_{w}\) à la paroi

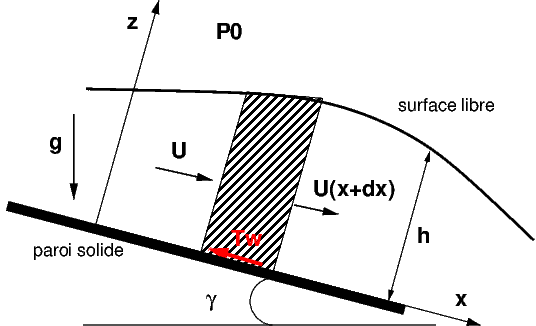
Fig. 4.6 modèle de Saint Venant

Bilan de masse sur une tranche de fluide \(hdxdy\)

\[\frac{\Delta\rho hdxdy}{\Delta t}-\rho U_{x}h_{x}dy+\rho U_{x+dx}h_{x+dx}dy=0\]

DL à l’ordre 1:

\[\frac{\partial h}{\partial t}+\frac{\partial hU}{\partial x}=0\]

bilan de quantité de mouvement sur une tranche de fluide \(hdxdy\)

\[\frac{\Delta\rho Uhdxdy}{\Delta t}+\rho\left(U^{2}h_{x+dx}-U^{2}h_{x}\right)dxdy=\left(-\Delta(\overline{p}h)+P_{0}\Delta h\right)dy+\left(\rho gh\sin\gamma-\tau_{w}\right)dxdy\]

répartition de pression hydrostatique suivant \(z\)

\[p=P_{0}+\rho g\cos(\gamma)(h-z)\Longrightarrow\overline{p}=P_{0}+\rho g\cos(\gamma)\frac{h}{2}\]

DL à l’ordre 1 avec \(\tau_{w}=C_{f}\rho U^{2}\)

\[\frac{\partial Uh}{\partial t}+\frac{\partial U^{2}h}{\partial x}=-g\cos(\gamma)h\frac{\partial h}{\partial x}+gh\sin(\gamma)-C_{f}U^{2}\]

si l’angle est petit: \(\gamma\ll 1\)

\[\frac{\partial Uh}{\partial t}+\frac{\partial U^{2}h}{\partial x}=\gamma gh-gh\frac{\partial h}{\partial x}-C_{f}U^{2}\]

On obtiens aisni les équation de St Venant, du nom de Adhémar-Jean-Claude Barré de Saint-Venant (ingénieur mathématicien français 1797-1886)

Équation avec surface libre

écoulement de vitesse moyenne \(\overrightarrow{U}(x,t)=U\overrightarrow{e_{x}}\) et de hauteur d’eau \(h(x)\)

\[\begin{split}\begin{aligned} \frac{\partial h}{\partial t}+\frac{\partial hU}{\partial x} & =0\\ \frac{\partial hU}{\partial t}+\frac{\partial U^{2}h}{\partial x} & =\gamma gh-gh\frac{\partial h}{\partial x}-C_{f}U^{2}\end{aligned}\end{split}\]

remarque: on peut les obtenir par dérivation à partir de Navier-Stokes en considérant les moyennes

\[U(x,t)=\frac{1}{h}\int_{_{0}}^{h}u(x,z,t)dz\]

En 2D équation avec surface libre

écoulement de vitesse moyenne \(\overrightarrow{U}(x,y)=U\overrightarrow{e_{x}}+V\overrightarrow{e_{y}}\) de hauteur \(h(x,y)\)

\[\begin{split}\begin{aligned} \frac{\partial h}{\partial t}+div(h\overrightarrow{U}) & =0\\ \frac{\partial h\overrightarrow{U}}{\partial t}+div(h\overrightarrow{U}\otimes\overrightarrow{U}) & =\gamma gh-gh\,\overrightarrow{grad}h-C_{f}\left|U\right|\,\overrightarrow{U}\end{aligned}\end{split}\]

le moteur de l’écoulement est la gravité qui compense le frottement au fond:

\[\gamma gh_{0}\sim C_{f}U_{0}^{2}\]

Les nombres sans dimension importants sont:

• nombre de Froude

\[Fr=\frac{U_{0}}{\sqrt{gh_{0}}}\]

• nombre de Reynolds

\[Re=\frac{U_{0}L}{\nu}\]

• la loi de frottement

\[C_{f}=C_{f}(Re)\]

4.2. Ondes de surface en eau peu profonde

dans le cas de petites perturbations dans le réfèrentiel suivant le mouvement moyen \(U_{0}\):

\(h=h_{0}+\delta h\), \(U= 0 + \delta u\)

Equations de propagation d’ondes de surface

\[\begin{split}\begin{aligned} \frac{\partial\delta h}{\partial t}+h_{0}\frac{\partial\delta u}{\partial x} & =0\\ h_{0}\frac{\partial\delta u}{\partial t}+gh_{0}\frac{\partial\delta h}{\partial x} & =0\end{aligned}\end{split}\]

c’est un système hyperbolique linéaire de propagation d’ondes, qui après élimination de \(\delta u\) donne:

Equations des ondes

\[\frac{\partial^{2}\delta h}{\partial t{}^{2}}-gh_{0}\frac{\partial^{2}\delta h}{\partial x{}^{2}}=0\]

cette équation traduit la propagation d’ondes de surface (vague) avec une célérité \(c_{0}=\sqrt{gh_{0}}\) (soit \(U_{0}\pm c_{0}\) dans le référentiel fixe)

4.2.1. Forme dimensionnelle

on pose \(h'=\delta h/h_{0}\), \(u'=\delta u/U_{0}\)

\[\begin{split}\begin{aligned} \frac{\partial h'}{\partial t'}+\frac{\partial u'}{\partial x'} & =0\\ Fr^{2}\frac{\partial u'}{\partial t'}+\frac{\partial h'}{\partial x'} & =0\end{aligned}\end{split}\]

système hyperbolique linéaire de propagation d’ondes

\[\frac{\partial^{2}h'}{\partial t'^{2}}-Fr^{-2}\frac{\partial^{2}h'}{\partial x'^{2}}=0\]

propagation d’ondes de surface (vague) avec une célérité

\[c_{0}=\sqrt{gh_{0}}\sim Fr^{-1}\]

La solution générale s’écrit:

\[h'(x,t)=F(x-c_{0}t)+G(x+c_{0}t)\]

• Onde simple: \(h'(x,t)=A\sin(kx-\omega t+\phi)=Ae^{\bm{i}k(x-ct)}+cc\)

• nombre d’onde \(k=\frac{2\pi}{\lambda}\), \(\lambda\) longueur d’onde

• pulsation \(\omega=\frac{2\pi}{T}=2\pi f\), \(T\) période, \(f\) fréquence

• vitesse de phase (célérité): \(v_{\phi}=\frac{\omega}{k}=c\)

• vitesse de groupe: \(v_{g}=\frac{d\omega}{dk}\)

\[\sin(kx-\omega t)+\sin(k'x-\omega't)=2\sin\underbrace{(\frac{k'+dk}{2}x-\frac{\omega+\omega'}{2}t)}_{v_{\phi}\approx\frac{\omega}{k}}\cos\underbrace{(\frac{k'-k}{2}x-\frac{\omega'-\omega}{2}t)}_{v_{g}\approx\frac{d\omega}{dk}}\]

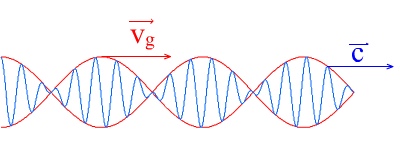
Fig. 4.7 vitesse de groupe

Fig. 4.8 animation vitesse de groupe (vert) versus phase (rouge)

Fig. 4.9 Ondes en eau peu profonde

en milieu peu profond \(L_{0}\gg h\)

déformation de la surface libre \(h'=Ae^{kx-\omega t}\) avec \(\omega=kc_{0}\)

La célérité \(c_{0}=\sqrt{gh}\) (vitesse de phase) est indépendante de \(k\), mais fonction de \(h\)

\(\Longrightarrow\) la vitesse de groupe \(v_{g}=c_{0}\) est constante (indépendante de \(k\)):

donc toutes les ondes se propagent à la même vitesse

\(\Longrightarrow\) pas de dispersion d’ondes, mais possibilité de déferlement si \(h\) varie

4.3. Modèle en eau profonde (océan)

Fig. 4.10 vagues sur l’océan

création des vagues par effet du vent puis propagation des vagues

attention milieu profond donc l’analyse précédente est non applicable

hypothèse:

• pas d’effet du fond (\(h_{0}\) tres grand) néglige \(\tau_{w}\)\(\leadsto\) fluide parfait incompressible

• écoulement potentiel (irrotationnel) \(\overrightarrow{U}=\overrightarrow{grad}\phi\)

• \(h'(x,y,t)\) est la fluctuation de la surface libre

• hauteur d’eau \(h(x,y,t)=h_{0}+h'(x,y,t)\)

• fond \(z=-h_{0}\)

Si \(\overrightarrow{U}=\overrightarrow{grad}\phi\) , alors

\[\overrightarrow{U}.\nabla\overrightarrow{U}=\overrightarrow{grad}(\frac{1}{2}U^{2})-\overrightarrow{U}\wedge\overrightarrow{rot}\,\overrightarrow{U}=\overrightarrow{grad}(\frac{1}{2}\left(\overrightarrow{grad}\phi\right)^{2})\]

Le système d’équations s’écrit alors:

\[\begin{split}\begin{aligned} \Delta\Phi & =0\\ \overrightarrow{grad}\left(\rho\frac{\partial\Phi}{\partial t}+\frac{\rho}{2}\left(\overrightarrow{grad}\phi\right)^{2}+p+\rho gz\right) & =0\end{aligned}\end{split}\]

On choisit d’écrire la pression sous la forme

\[p(x,y,z,t)=p_{0}-\rho gz-\rho\frac{\partial\Phi}{\partial t}-\frac{\rho}{2}\left(\overrightarrow{grad}\phi\right)^{2}\]

avec les conditions suivantes:

• cdt limite au fond en \(z=-h_{0}\)(paroi impermeable \(Uz=0\)) \(\frac{\partial\Phi}{\partial z}=0\)

• cdt limite à la surface libre en \(z=h'(x,y,t)\): \(V_{z}=\frac{Dh}{Dt}\) et \(p=p_{0}\)

Le système d’équations s’écrit alors:

Equations d’Airy

(4.1)\[\begin{eqnarray} \frac{\partial h}{\partial t}+\frac{\partial h}{\partial x}\frac{\partial\Phi}{\partial x}+\frac{\partial h}{\partial y}\frac{\partial\Phi}{\partial y}-\frac{\partial\Phi}{\partial z}&=&0\\ \frac{\partial\Phi}{\partial t}+\frac{1}{2}\left(\overrightarrow{grad}\phi\right)^{2}&=& -gh'\\ \end{eqnarray}\]

4.4. Ondes de surface en eau profonde

Pour de petits mouvements \(h'(x,t)\ll1\): on cherche une solution sous la forme d’une onde:

\[\phi(x,z,t)=A(z)e^{i\,k(x-ct)}\]

solution de l’équation:

\[\Delta\Phi=\frac{d^{2}A}{dz^{2}}-k^{2}A=0\]

La solution est de la forme

\[A(z)=A_{0}cosh(k(z+h_{0}))\]

qui vérifie la cdt \(\frac{\partial\Phi}{\partial z}=0\) sur le fond \(z=-h_{0}\)

Cette solution vérifie les cdts (linéarisées) sur la surface libre: \(z=h' \mbox{ avec } h_{0}+h'\approx h_{0}\)

En notant \(c\) la célérité et en reportant dans l’équation, il vient

\[\frac{\partial\Phi(x,h,t)}{\partial t}=-gh'\Longrightarrow h'= i\frac{kc}{g}A_{0}sinh(kh_{0})e^{i\,k(x-ct)}\]

\[\frac{\partial h'}{\partial t}=\frac{\partial\Phi(x,h,t)}{\partial z}=0\Longrightarrow\frac{k^{2}c^{2}}{g}A_{0}cosh(kh_{0})e^{i\,k(x-ct)}=kA_{0}sinh(kh_{0})e^{i\,k(x-ct)}\]

d’où la relation sur la célérité:

\[c^{2}=\frac{g}{k}\tanh(kh_{0}) \mbox{ soit } \omega^{2}=k^{2}c^{2}=gk\tanh(kh_{0})\]

• en eau profonde \(kh_{0}\gg1\) : \(tanh(kh_{0})\approx1\)
  on obtiens des ondes dispersives

\[v_{g}=\frac{d\omega}{dk}=\frac{1}{2}\sqrt{\frac{g}{k}}\neq c=\sqrt{\frac{g}{k}}\sim\sqrt{g\lambda}\,\mbox{ avec }\lambda=\frac{2\pi}{k}\]

• en eau peu profonde \(kh_{0}\ll1\): \(tanh(kh_{0})\approx kh_{0}\)
  on obtiens des ondes non dispersives

\[v_{g}=c\sim\sqrt{gh_{0}}\]

Les paramètres pour les ondes en eau profonde sont :

• Onde simple: \(h'(x,t)=A\sin(kx-\omega t+\phi)=Ae^{i\,k(x-ct)}+cc\)

• nombre d’onde \(k=\frac{2\pi}{\lambda}\), \(\lambda\) longueur d’onde

• pulsation \(\omega=\frac{2\pi}{T}=2\pi f\), \(T\) période, \(f\) fréquence

• vitesse de phase (célérité): \(v_{\phi}=\frac{\omega}{k}=c\)

• vitesse de groupe: \(v_{g}=\frac{d\omega}{dk}\)

\[\sin(kx-\omega t)+\sin(k'x-\omega't)=2\sin\underbrace{(\frac{k'+dk}{2}x-\frac{\omega+\omega'}{2}t)}_{v_{\phi}\approx\frac{\omega}{k}}\cos\underbrace{(\frac{k'-k}{2}x-\frac{\omega'-\omega}{2}t)}_{v_{g}\approx\frac{d\omega}{dk}}\]

Fig. 4.11 vitesse de groupe (vert) et de phase (rouge)

• \(U=i\,kA_{0}cosh(k(z+h_{0}))e^{i\,k(x-ct)}\mbox{ et }W=kA_{0}sinh(k(z+h_{0}))e^{\bm{i}k(x-ct)}\)

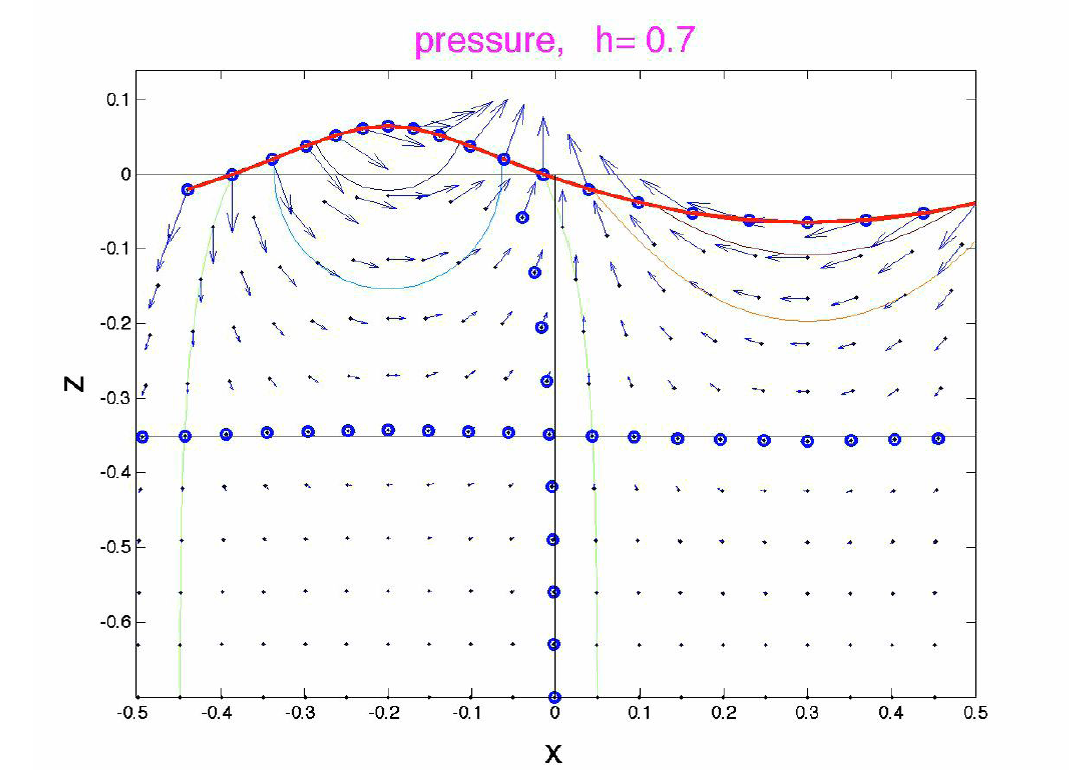
Fig. 4.12 Ondes de surface

Fig. 4.13 Propagation de vagues

Fig. 4.14 animation de la propagation de vagues

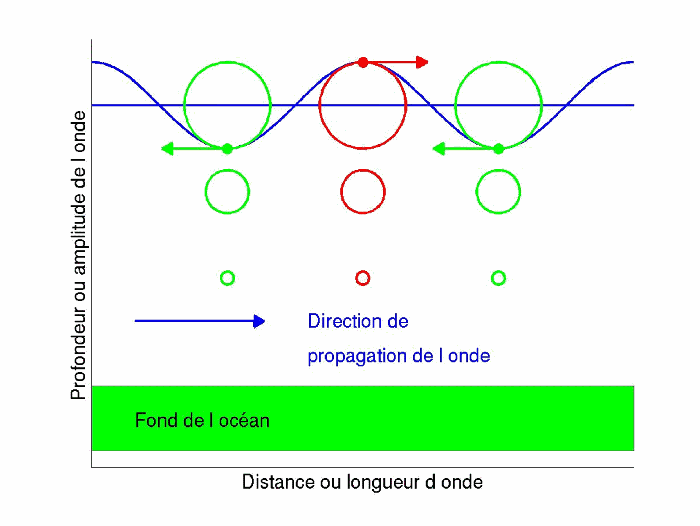
Fig. 4.15 houle

• mouvement des particules: oscillations sur un cercle (ellipse)

• Attention il y a propagation d’énergie et non transport des particules !

Fig. 4.16 déferlement de vague

Près des cotes \(c\approx\sqrt{gh}\) lorsque \(h\rightarrow0\) on \(c\nearrow\), accélération et raidissement du profil. D’où formation d’un front et déferlement

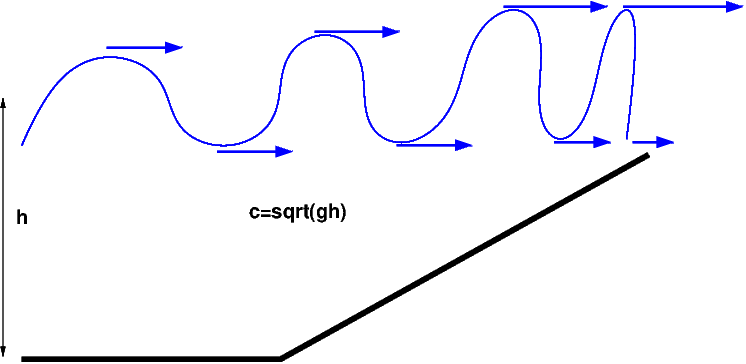
Fig. 4.17 principe du déferlement de vague

Quand la direction des houles est oblique par rapport à la côte, donc aux isobathes (lignes d’égale profondeur), la vitesse de propagation de la houle (\(c\)) ne va pas être identique en tous points de la crête. Elle est moins rapide là où la profondeur est plus faible. Les points de la ligne de crête les plus proches du rivage vont ralentir par rapport aux points les plus éloignés et la houle va donc tourner et tendre à devenir parallèle à la côte.

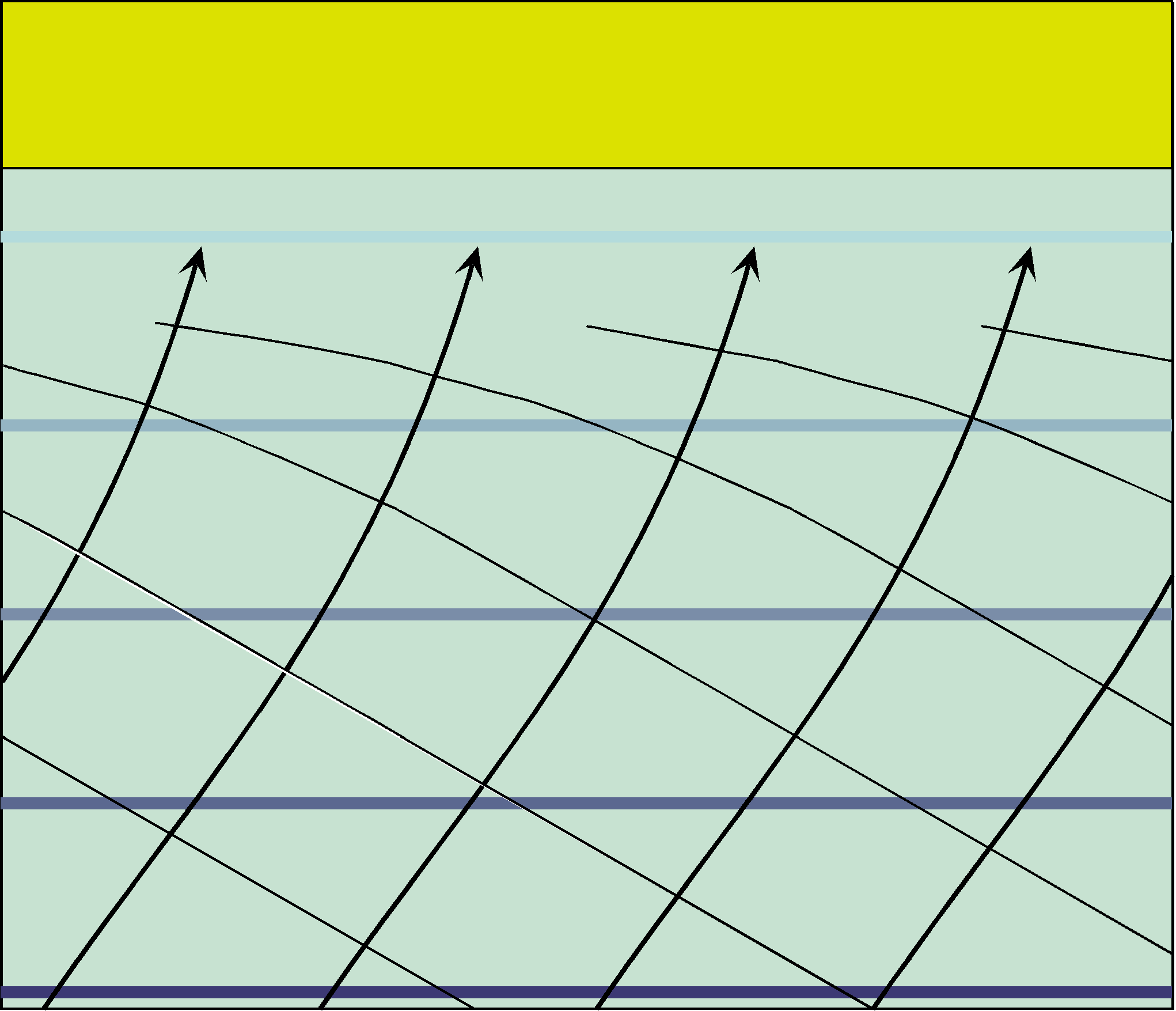
Fig. 4.18 houle sur la cote: en noir crêtes de houle, en bleu, isobathes

Le déferlement survient lorsque la houle arrive près de la côte (phénomène de réfraction)[2]. En effet, lorsque la houle se rapproche du rivage, sa célérité ne dépend que de la profondeur locale et diminue avec cette dernière. La longueur d’onde de la houle, étant liée à la célérité diminue aussi avec la profondeur locale. Par conséquent, ces lignes de crêtes ont tendance à se resserrer près de la côte. Ainsi, la densité d’énergie par unité de surface augmente (par conservation de l’énergie), ce qui entraîne l’augmentation de la hauteur de la vague. La hauteur augmente jusqu’à une certaine limite. En effet, lorsque la hauteur atteint 0.78 fois la profondeur, la vague devient instable et déferle

• la vitesse de propagation \(c\) des ondes devient fonction de la vitesse \(U\)

• nombre caractéristique \(M=U/c\) analogue au nombre de Mach

• phénoménes de ressaut hydraulique (analogue au choc) si \(M>1\)

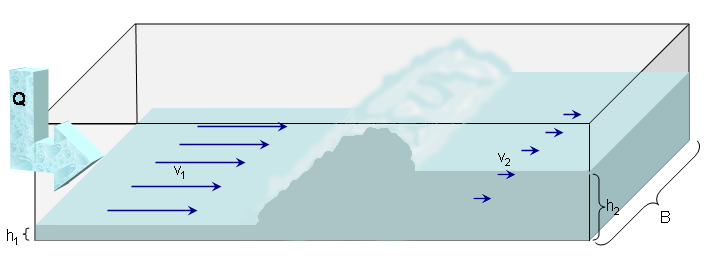
Fig. 4.19 ressaut hydraulique

type d” écoulement suivant le nombre de Froude \(Fr=\frac{U_{0}}{\sqrt{gh_{0}}}\)

• écoulement torrentiel \(Fr>1\)

• écoulement fluvial \(Fr<1\)

ressaut: passage torrentiel à fluvial (avec dissipation d’énergie)

Fig. 4.20 expérience de ressaut

• accélération du fluide en 2 (sur le barrage) \(>\) vitesse critique

• transition vers régime fluviale en 4 \(<\) vitesse critique

• Bernoulli sur la surface libre

  \[E=gh+\frac{1}{2}u^{2}=cste\]

• Bilan masse

  \[Q=hu=cste\]

• comparaison de \(u\) par rapport à \(\sqrt{gh_{0}}\)

Fig. 4.21 ressaut hydraulique

Fig. 4.22 ressaut hydraulique

• vagues d’étrave suivant la valeur de \(M\)

Fig. 4.23 vague d’étrave autour d’un canard

Fig. 4.24 vague d’étrave autour d’un navire

Soliton = onde solitaire qui se propage dans les milieux non linéaires et dispersifs avec une énergie localisée dans l’espace (stable)

• découvert par John Scott Russell en 1834

• tsunamis, mascarets ou vagues scélérates

Fig. 4.25 Mascaret

Fig. 4.26 Tsunami