2. Lois fondamentales locales

2.1. Expérience préliminaire

On considère un écoulement stationnaire, dont la vitesse \(U\) est parallèle à l’axe \(Ox\). On isole (par la pensée ou en trouvant un moyen de visualisation, coloration par exemple) des « particules fluides », que l’on suit dans leurs mouvements. On suit des particules fluides dans cet écoulement et on effectue des mesures de masse volumique, de vitesse et de pression:

1. en des points A,B,C fixes (approche eulérienne),

2. en suivant les particules fluides dans leur mouvement (approche lagrangienne).

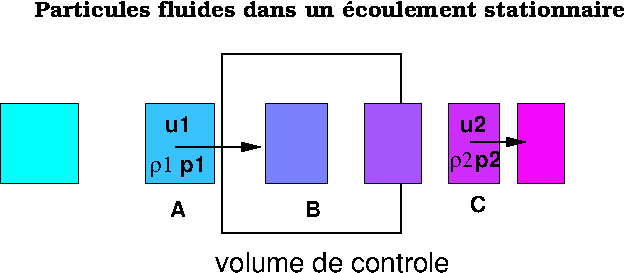
Fig. 2.17 Schéma de l’expérience préliminaire

La vidéo suivante montre la trajectoire et la déformation des particules fluides lors de cette expérience:

2.1.1. Mesures eulériennes

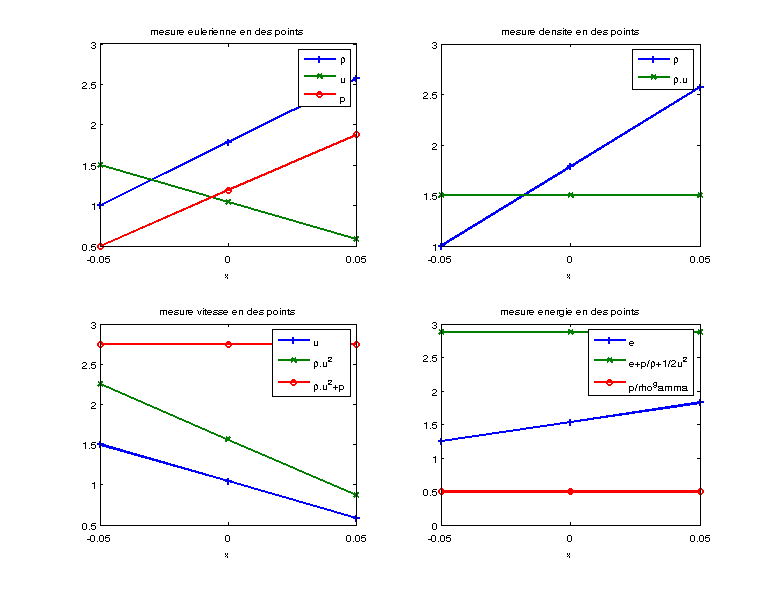
Fig. 2.18 courbes des mesures eulériennes fonction de l’espace

2.1.2. Mesures lagrangiennes

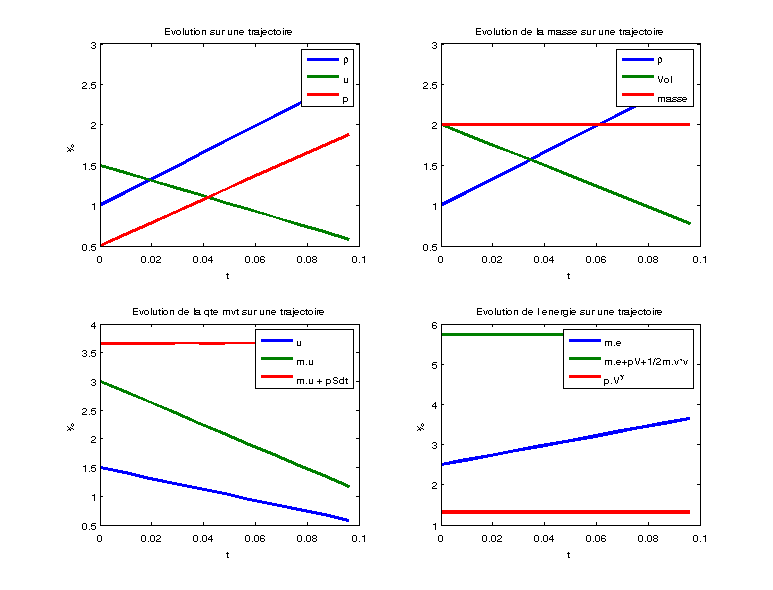
Fig. 2.19 courbes des mesures lagrangiennes fonction du temps

2.2. Description Eulérienne

Un fluide en mouvement est définit par des grandeurs physiques:

1. la masse volumique \(\rho\) en \(kg/m^{3}\) (nbre de molécules/unité de volume):
   ex air \(\rho=1kg/m^{3}\)

2. la vitesse \(\overrightarrow{U}\) en \(m/s\) qui a 3 composantes \(\{u,v,w\}\) : (vitesse moyenne macroscopique)
   ex \(U=220\,m/s\) pour un avion de ligne à 800 km/h

3. la pression \(p\) en \(Pa\) : ( force (choc) exercée par les molécules à la surface de la particule)
   ex pression atmosphérique \(p=10^{5}Pa\)

4. la température \(T\) en K: (agitation moléculaire des molécules)
   ex \(T=300\,K\) pour T=\(27^{\circ}C\)

qui sont gouvernées par des équations de bilan qui traduisent les principes fondamentaux de la mécanique, à savoir:

1. la conservation de la masse

2. le principe fondamentale de la dynamique

3. le principe fondamentale de la thermodynamique

et par une relation thermodynamique supplémentaire (équation d’état), qui permet de fermer le problème.

Pour décrire l’évolution de ces grandeurs, on ne choisit pas de suivre les particules fluides dans leur mouvement (description lagrangienne où l’observateur se déplace avec le même mouvement que les particules).

On choisit une approche eulérienne où l’observateur est à une position fixe et regarde passer les particules fluides. Pour écrire les équations de bilan, on choisit un élément de volume \(dxdydz\) situé à une abscisse \((x,y,z)\) dans un repère fixe. Les grandeurs physiques dépendent alors du point d’observation \(\overrightarrow{X}=(x,y,z)\) et du temps \(t\):

\[\rho=\rho(\overrightarrow{X},t),\,\overrightarrow{U}=\overrightarrow{U}(\overrightarrow{X},t),\,p=p(\overrightarrow{X},t),\,T=T(\overrightarrow{X},t)\]

Si on suit cette description, l’observateur verra passé les particules fluides. Si on veut suivre une particule M (dont la position est \(M_{0}\) à t=0) au cours du temps, on calculera sa trajectoire, qui est tangente à chaque instant au vecteur vitesse:

\[\frac{D\overrightarrow{OM}}{Dt}=\overrightarrow{U}(\overrightarrow{OM},t)\,\mbox{ avec }\,\overrightarrow{OM}(t=0)=\overrightarrow{OM}_{0}\]

A un instant \(t_{1}\) fixé, on peut calculer les lignes de courant de l’écoulement qui sont les lignes \(\psi=cste\) tangentes en chaque point au vecteur vitesse.

Prudence

Les lignes de courant et les trajectoires sont en général différentes sauf pour un écoulement stationnaire (dont les propriétés ne dépendent pas du temps).

Pour calculer l’accélération d’une particule, on doit suivre cette particule: on note \(\frac{D}{Dt}\) la dérivée particulaire ( i.e. le long de la trajectoire), et \(\frac{\partial}{\partial t},\frac{\partial}{\partial x},\frac{\partial}{\partial y},\frac{\partial}{\partial z}\) les dérivées partielles eulériennes (i.e. en un point fixe de l’espace):

\[\begin{split}\begin{aligned} \overrightarrow{\gamma}= & \frac{D\overrightarrow{^{2}OM}}{Dt^{2}}=\frac{D}{Dt}(\overrightarrow{U}(\overrightarrow{OM}(t),t))=\frac{\partial\overrightarrow{U}}{\partial t}+\frac{D\overrightarrow{OM}}{Dt}.\overline{\overline{grad}}\,\overrightarrow{U}\\ \overrightarrow{\gamma}= & \left[\begin{array}{c} \frac{\partial u}{\partial t}\\ \frac{\partial v}{\partial t}\\ \frac{\partial w}{\partial t} \end{array}\right]+\overrightarrow{U}\left[\begin{array}{c} \overrightarrow{grad}\,u\\ \overrightarrow{grad}\,v\\ \overrightarrow{grad}\,w \end{array}\right]\end{aligned}\end{split}\]

L’opérateur gradient que l’on note \(\overrightarrow{grad}\) est aussi souvent noté \(\overrightarrow{\nabla}\).

Dérivée particulaire

Pour calculer la variation d’une quantité le long d’une trajectoire, on définit la dérivée particulaire (ou dérivée le long de la trajectoire):

\[\frac{D()}{Dt}=\frac{\partial}{\partial t}+\frac{\partial}{\partial x}\frac{dx}{dt}+\frac{\partial}{\partial y}\frac{dy}{dt}+\frac{\partial}{\partial z}\frac{dz}{dt}=\frac{\partial()}{\partial t}+\overrightarrow{U}.\overrightarrow{\nabla}()\]

2.3. Équation de bilan générale

Pour simplifier l’exposé, nous allons considérer un écoulement bidimensionnel plan(i.e. dont les propriétés ne varient pas suivant z, et dont la composante de vitesse suivant z est nulle). On choisit un élément de volume, dessiné sur la figure suivante, de cotés dx et dy , et d’épaisseur dz.

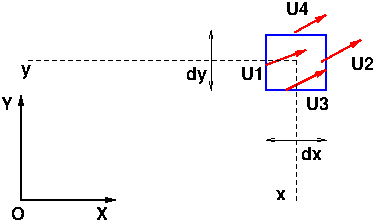
Fig. 2.20 Bilan sur un volume de contrôle

La vitesse du fluide \(\overrightarrow{U}(x,y,t)\) est différente suivant les faces de l’élément:

\[\overrightarrow{U_{1}}=\overrightarrow{U}(x-\frac{dx}{2},y,t),\,\overrightarrow{U_{2}}=\overrightarrow{U}(x+\frac{dx}{2},y,t),\,\overrightarrow{U_{3}}=\overrightarrow{U}(x,y-\frac{dy}{2},t),\,\overrightarrow{U_{4}}=\overrightarrow{U}(x,y+\frac{dy}{2},t)\]

Soit \(f(x,y,t)\) une grandeur physique du fluide par unité de masse, la quantité de \(f\) dans l’élément vaut \(\rho f dV\). Dans une description eulérienne, la variation de \(f\) dans l’élément est due à la variation temporelle de \(\rho f\) (car on fait le bilan dans un élément fixe \(dV\) dans l’espace):

\[\left(\rho f(t+dt,x,y,z)-\rho f(t,x,y,z)\right) dxdydz=\frac{\partial \rho f}{\partial t} dt\,dV\]

Cette variation est égale à la somme:

1. de la quantité de \(f\) crée dans l’élément par des termes sources \(S\) (par unité de volume)

2. un bilan de la quantité de \(f\) qui rentre et qui sort de l’élément à travers sa surface.

Ce second terme correspond à un bilan des flux \(\Delta F\) de \(\rho f\) à travers les facettes de l’élément. On distingue des fluxs convectifs (liés au transport par les particules fluides) et des flux de diffusion (liés à l’agitation moléculaire).

2.3.1. flux convectifs

Pour une facette de surface \(dS\), de normale \(\overrightarrow{n}\), sur laquelle la vitesse du fluide est égale à \(\overrightarrow{U}\), le flux de convection \(F_c\) de \(f\) à travers la facette correspond à la quantité de \(f\) transportée par le fluide qui passe à travers la facette par unité de temps. La quantité de \(f\) traversant la facette pendant \(dt\) s’écrit:

\[F_c\, dt = f*\underbrace{(\rho(\overrightarrow{U}.\overrightarrow{n})dt*dS)}_{\mbox{masse traversant la facette}}\]

2.3.2. flux de diffusion

Le flux de diffusion \(F_d\) est la quantité de \(f\) qui passe à travers une facette \(dS\) de normale \(\overrightarrow{n}\) par unité de temps du à l’agitation moléculaire et à la variation de \(f\) à travers la facette.

Ce flux est proportionnel au gradient de \(f\) (loi de Fourier pour la température, loi de Fick pour la concentration) avec un coefficient de diffusion \(\lambda\) fonction du fluide. La quantité de \(f\) qui traverse la facette pendant \(dt\) par diffusion s’écrit:

\[F_{d}\, dt =-\lambda\,\overrightarrow{grad}(f)\,.\overrightarrow{n}\, dS\, dt=-\lambda\frac{\partial f}{\partial n}dS\, dt\]

2.3.3. bilan des flux

Pour le calcul du bilan de flux à travers les facettes de l’élément, on oriente la normale vers l’extérieure: un flux sortant est donc compté positif.

L’équation de bilan s’écrit sous la forme générale suivante (avec la convention d’orientation de la normale):

\[ \underbrace{\frac{\partial(\rho f)}{\partial t}\,dV\,dt}_{\mbox{variation de }\rho f} = + \underbrace{S\,dV\,dt}_{\mbox{termes sources}} - \underbrace{\Delta F_c\,dt}_{\mbox{flux de convection}} - \underbrace{\Delta F_d\,dt}_{\mbox{flux de diffusion}} \]

2.3.3.1. bilan des fluxs de convection

Le bilan des flux de convection s’écrit donc en faisant le bilan sur les facettes de l’élément (en tenant compte du fait que l’écoulement est bidimensionnel plan et donc \(\overrightarrow{U}.\overrightarrow{n}=0\) sur les facettes \(z-\frac{dz}{2}\) et \(z+\frac{dz}{2}\)). Ce bilan s’écrit avec les notations de la figure précédente:

(2.12)\[\begin{eqnarray} \Delta F_c\,dt &=&\rho_{1}f_{1}\overrightarrow{U_{1}}.\overrightarrow{n_{1}}dtdydz+\rho_{2}f_{2}\overrightarrow{U_{2}}.\overrightarrow{n_{2}}dtdydz\\ &+&\rho_{3}f_{3}\overrightarrow{U_{3}}.\overrightarrow{n_{3}}dtdxdz+\rho_{4}f_{4}\overrightarrow{U_{4}}.\overrightarrow{n_{4}}dtdxdz \end{eqnarray}\]

avec

\[\begin{split}\begin{aligned} \rho_{1}f_{1}=\rho f(x-\frac{dx}{2},y,t), & \overrightarrow{n}_{1}=\left[\begin{array}{c} -1\\ 0\\ 0 \end{array}\right], & \overrightarrow{U_{1}}.\overrightarrow{n_{1}}=-u(x-\frac{dx}{2},y,t)\\ \rho_{2}f_{2}=\rho f(x+\frac{dx}{2},y,t), & \overrightarrow{n}_{2}=\left[\begin{array}{c} +1\\ 0\\ 0 \end{array}\right], & \overrightarrow{U_{2}}.\overrightarrow{n_{2}}=u(x+\frac{dx}{2},y,t)\\ \rho_{3}f_{3}=\rho f(x,y-\frac{dy}{2},t), & \overrightarrow{n}_{3}=\left[\begin{array}{c} 0\\ -1\\ 0 \end{array}\right], & \overrightarrow{U_{3}}.\overrightarrow{n_{3}}=-v(x,y-\frac{dy}{2},t)\\ \rho_{4}f_{4}=\rho f(x,y+\frac{dy}{2},t), & \overrightarrow{n}_{4}=\left[\begin{array}{c} 0\\ +1\\ 0 \end{array}\right], & \overrightarrow{U_{4}}.\overrightarrow{n_{4}}=v(x,y-\frac{dy}{2},t)\end{aligned}\end{split}\]

ce qui donne en regroupant les termes:

\[\begin{split}\begin{aligned} \Delta F_c \,dt & = & \left\{ \rho f(x+\frac{dx}{2},y,t)*u(x+\frac{dx}{2},y,t)-\rho f(x-\frac{dx}{2},y,t)*u(x-\frac{dx}{2},y,t)\right\} dtdydz\\ & + & \left\{ \rho f(x,y+\frac{dy}{2},t)*v(x,y+\frac{dy}{2},t)-\rho f(x,y-\frac{dy}{2},t)*v(x,y-\frac{dy}{2},t)\right\} dtdxdz\end{aligned}\end{split}\]

En effectuant un développement limité, et en ne conservant que les termes au premier ordre (les termes d’ordre supérieure ont une contribution qui tend vers zero), il vient:

\[\Delta F_c\,dt=\left\{ \frac{\partial}{\partial x}(\rho fu)+\frac{\partial}{\partial y}(\rho fv)\right\} dxdydz\,dt=div(\rho f\overrightarrow{U})dV\,dt\]

2.3.3.2. bilan des flux de diffusion

Le bilan des flux de diffusion à travers les facettes de l’élément s’écrit:

\[\begin{split}\begin{aligned} \Delta F_{d}\,dt & =+\lambda_{1}\frac{\partial f}{\partial x}\mid_{1}dtdydz-\lambda_{2}\frac{\partial f}{\partial x}\mid_{2}dtdydz\\ & +\lambda_{3}\frac{\partial f}{\partial y}\mid_{3}dtdxdz-\lambda_{4}\frac{\partial f}{\partial y}\mid_{4}dtdxdz\end{aligned}\end{split}\]

ce qui donne après un développement limité à l’otdre 1:

\[\Delta F_{d}\,dt =-div(\lambda\overrightarrow{grad}(f))=-div(\lambda\overrightarrow{\nabla}f)\]

2.3.4. équation de bilan générale

La variation de \(f\) pendant \(\Delta t\) dans l’élément \(dxdydz\) s’écrit donc de façon générale (en 2D et 3D):

\[ \underbrace{\frac{\partial}{\partial t}(\rho f)\;dVdt}_{\mbox{variation temporelle}} +\underbrace{div(\rho f\overrightarrow{U})dVdt}_{\mbox{flux convectif}} -\underbrace{div(\lambda\overrightarrow{grad}f)dVdt}_{\mbox{flux diffusif}} = \underbrace{S dV dt}_{\mbox{terme source}} \]

L’équation de bilan d’une quantité scalaire \(f\) par unité de masse s’écrit en Eulérien sous la forme suivante:

forme conservative de l’équation de bilan de f

\[ \underbrace{\frac{\partial}{\partial t}\left\{ \rho f\right\} }_{variation\,temporelle}+\underbrace{div(\rho f\overrightarrow{U})}_{flux\, convectif}-\underbrace{div(\lambda\overrightarrow{\nabla}f)}_{flux\, diffusif}=\underbrace{S}_{terme\, source}\]

Au lieu de faire un bilan sur un petit élément de volume, on peut suivre une particule fluide dans son mouvement et calculer l’évolution de \(f\) le long de sa trajectoire. On utilise alors la dérivée particulaire et on montre que l’on obtiens l’équation suivante:

forme lagrangienne d’évolution de f

\[\rho \frac{D\,f}{Dt} = \underbrace{\rho \frac{\partial\,f}{\partial t} }_{terme\, instationnaire} + \underbrace{\rho \overrightarrow{U}.\overrightarrow{grad}(f)}_{terme\, convection} = \underbrace{div(\lambda\overrightarrow{\nabla}f)}_{terme\, diffusion}+ \underbrace{S}_{terme\, source}\]

En utilisant l’équation de conservation de la masse, on montre que ces deux équations sont équivalentes.

Note

En utilisant le théorème de la divergence ou Green-Ostrogradski, on peut calculer directement le bilan des flux sur la frontière avec un formalisme d’analyse vectorielle.

théorème de la divergence

Pour tout champ de vecteur \(F\), son flux à travers une surface fermée \(S\) est égale à l’intégrale de la divergence dans le volume \(V\) limitée par \(S\):

\[ \oint_S \overrightarrow{F}.\overrightarrow{n} dS = \iiint_V div(\overrightarrow{F}) dV\]

Appliquée à un petit élément de volume \(dV\), cela donne:

\[ \sum_{\mbox{faces}} \overrightarrow{F}.\overrightarrow{n}\,dS = div(\overrightarrow{F})\,dV \]

qui est la relation que l’on a obtenu par calcul directe et développement limité à l’ordre 1.

2.4. Bilan de masse

Important

La première équation de conservation traduit la conservation de la masse

Pour un fluide monophasique sans création de masse, la variation de masse \(\Delta\rho\) dans l’élément \(dxdydz\) est nulle. D’après ce qui précède, elle est égale à la somme de la variation temporelle dans l’élément et du bilan des flux de masse entrants et sortants de l’élément:

\[ \frac{\Delta\rho}{\Delta t}=\frac{\partial\rho}{\partial t} dxdydz+div(\rho\overrightarrow{U})dxdydz=0 \]

ce qui s’écrit après simplification sous la forme suivante dite (forme conservative)

forme conservative du bilan de masse

\[\underbrace{\frac{\partial\rho}{\partial t}}_{variation\,temporelle} + \underbrace{div(\rho\overrightarrow{U})}_{flux\,de\,masse}=0\]

soit

\[\frac{\partial\rho}{\partial t}+\frac{\partial\rho u}{\partial x}+\frac{\partial\rho v}{\partial y}+\frac{\partial\rho w}{\partial z}=0\]

En décomposant, on obtient la forme non-conservative ou convective

forme lagrangienne de la conservation de masse

\[\underbrace{\frac{\partial\rho}{\partial t}+\overrightarrow{U}.\overrightarrow{grad}\,\rho}_{\mbox{variation }\frac{D\rho}{Dt}}+\underbrace{\rho\,div(\overrightarrow{U})}_{\mbox{variation de volume}}=0\]

qui doit traduire le fait que la masse d’une particule fluide \(m=\rho V\) doit se conserver le long de sa trajectoire, i.e.:

\[ \frac{D m}{Dt} = V \frac{D \rho}{Dt} + \rho \frac{D V}{Dt} = 0 \]

On note donc que \(div(\overrightarrow{U})\) représente la variation de volume du fluide par unité de temps:

\[div(\overrightarrow{U})=\frac{1}{V}\frac{DV}{Dt}\]

Par exemple pour la compression 1D illustrée sur la figure ci-dessous,

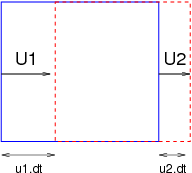
Fig. 2.21 variation de volume pour une compression 1D

la variation de volume est liée à la variation de la longueur \(\Delta M_1M_2\) suivant x de la particule pendant un temps \(dt\)

(2.13)\[\begin{eqnarray} \Delta M_1M_2 &=& (M_2(t+dt) - M_2(t)) - (M_1(t+dt)-M_1(t))\\ &=& u_2 (x+dx) dt - u_1(x) dt \end{eqnarray}\]

ce qui donne la variation de volume \(\Delta V\)

\[ \Delta V = \Delta M_1M_2 dydz = \frac{\partial u}{\partial x} dxdydzdt = div\overrightarrow{U} V dt \]

L’équation de conservation de la masse s’écrit donc (en suivant le mouvement d’une particule fluide) :

\[\frac{1}{\rho}\frac{D\rho}{Dt}+\frac{1}{V}\frac{DV}{Dt}=0\,\,\,\,\,\equiv\,\,\,\,\,\frac{D\rho V}{Dt}=0\]

On a une interprétation mécanique de l’équation de bilan de masse:

Important

la masse \(m=\rho V\) d’une particule fluide est constante.

La variation de la masse volumique d’une particule fluide est donc due à la variation de son volume mesurée par \(div \overrightarrow{U}\)

Si le fluide est incompressible, la masse volumique d’une particule fluide est constante, i.e.:

\[\frac{D\rho}{Dt}=\frac{\partial\rho}{\partial t}+\overrightarrow{U}.\overrightarrow{grad}\,\rho=0\]

Son volume est donc constant, et on en déduit que le champ de vitesse d’un fluide incompressible doit être à divergence nulle:

\[div\,\overrightarrow{U}=0\]

2.5. Bilan de quantité de mouvement

Important

La seconde équation de conservation traduit la loi fondamentale de la dynamique (loi de Newton)

La variation de la quantité de mouvement dans l’élément \(dxdydz\) est égale à la somme des efforts appliqués.

\[\frac{\Delta\rho\overrightarrow{U}}{\Delta t} dxdydz = \sum\overrightarrow{F}\]

La variation de quantité de mouvement comprend 2 termes:

1. un terme instationnaire traduisant la variation temporelle de \(\rho\overrightarrow{U}\)

2. un terme de flux convectif, traduisant l’apport de quantité de mouvement par le fluide traversant la frontière de l’élément.

En considérant la composante suivant x de la quantité de mouvement: \(\rho u\), sa variation dans l’élément s’écrit d’après ce qui précède:

\[ \frac{\Delta \rho u}{\Delta t} dV = \frac{\partial \rho u}{\partial t} dV + div(\rho u \overrightarrow{U}) \]

ce qui permet d’écrire la variation de quantité de mouvement sous forme vectorielle suivante:

\[ \frac{\Delta\rho\overrightarrow{U}}{\Delta t} = \frac{\partial\rho\overrightarrow{U}}{\partial t}+div(\rho\overrightarrow{U}\otimes\overrightarrow{U}) \]

Les efforts extérieurs appliqués sur l’élément sont:

• des forces volumiques: la gravité \(\overrightarrow{g}\rho dxdydz\), les forces éléctro-magnétiques, …

• des forces surfaciques: interaction des autres particules fluides sur l’élément

Pour un fluide, ces forces surfaciques sont modélisées sous forme tensorielle par \(\overline{\overline{\sigma}}\otimes\overrightarrow{n}\, dS\), avec \(\overline{\overline{\sigma}}\) le tenseur des contraintes qui dépend de la pression \(p\) et du tenseur des déformations \({D}_{ij}=\frac{1}{2}(\frac{\partial U_{i}}{\partial x_{j}}+\frac{\partial U_{j}}{\partial x_{i}})\))

La force de contrainte (modélisé par le tenseur des contraintes \(\overline{\overline{\sigma}}\)) comprends:

• des forces normales de pression: \(-p\overrightarrow{n}dS\) (qui existent même pour un fluide au repos)

• des forces de viscosité (tenseur \(\overline{\overline{\sigma_{v}}}\)) qui dépendent du tenseur des déformations \(\overline{\overline{D}}\)

Pour un fluide Newtonien (avec l’hypothèse de Stokes \(\lambda+\frac{2}{3}\mu=0\) ), la contrainte visqueuse dans la direction \(\overrightarrow{n}\) s’écrit:

\[\overline{\overline{\sigma_v}}\otimes\overrightarrow{n}=(\lambda div\,\overrightarrow{U})\overrightarrow{n}+2\mu\overline{\overline{D}}\otimes\overrightarrow{n}\]

Pour un fluide incompressible, l’expression du tenseur des contraintes visqueuses \(\overline{\overline{\sigma_v}}\) se simplifie (car \(div\overrightarrow{U}=0\))

\[\overline{\overline{\sigma_v}} = \mu\left(\overrightarrow{\nabla}\overrightarrow{U} + \overrightarrow{\nabla}^t\overrightarrow{U} \right)\]

soit

\[\overline{\overline{\sigma_v}}_{,ij}= \mu\left(\frac{\partial U_{i}}{\partial x_{j}}+\frac{\partial U_{j}}{\partial x_{i}}\right)\]

On retrouve l’expression classique de la contrainte de cisaillement à la paroi en notant \(u\) la vitesse près de la paroi (qui est parallèle à la paroi) et \(y\) la direction normale à la paroi.

\[\tau=\mu\frac{\partial u}{\partial y}|_{paroi}\]

2.5.1. bilan des forces de pression

Pour un fluide les forces surfaciques de pression \(F_p\) sont des forces normales à la surface: $\(F_p = -p\overrightarrow{n}dS\)$ qui existent même pour un fluide au repos.

La somme des forces de pression s’écrit pour l’élément considéré:

\[\sum\overrightarrow{F_p}=\left(p(x-\frac{dx}{2},y,t)-p(x+\frac{dx}{2},y,t)\right)dydz\,\overrightarrow{e_{x}}+\left(p(x,y-\frac{dy}{2},t)-p(x,y+\frac{dy}{2},t)\right)dxdz\,\overrightarrow{e_{y}}\]

En effectuant un développement limité à l’ordre 1, on obtient:

\[\sum\overrightarrow{F_p}=-\frac{\partial p}{\partial x}dxdydz\,\overrightarrow{e_{x}}-\frac{\partial p}{\partial y}dxdydz\,\overrightarrow{e_{y}} = - \overrightarrow{grad}\,p\,dV\]

2.5.2. bilan des forces de viscosité

Pour un fluide incompressible, le bilan des forces de viscosité \(F_v = \overline{\overline{\sigma_v}}\otimes\overrightarrow{n}\, dS\) sur toute la surface de l’élément se calcule de la même façon.

En effectuant un développement limité à l’ordre 1, on obtient:

\[ \sum\overrightarrow{F_v}=div\left(\mu(\nabla\overrightarrow{U}+\nabla^{t}\overrightarrow{U})\right) dV \]

Dans le cas compressible, on a un terme supplémentaire $\( \sum\overrightarrow{F_v}=div\left(\mu(\nabla\overrightarrow{U}+\nabla^{t}\overrightarrow{U})\right) dV + \overrightarrow{grad}\,\left(\lambda div\overrightarrow{U}\right)dV \)$

2.5.3. bilan de quantité de mouvement:

En utilisant les expressions précédentes, l’équation de bilan s’écrit:

\[\frac{\Delta\rho\overrightarrow{U}}{\Delta t} dV =\left[\rho\overrightarrow{g}+\overrightarrow{grad}\left(-p+\lambda div\overrightarrow{U}\right)+div\left(\mu(\nabla\overrightarrow{U}+\nabla^{t}\overrightarrow{U})\right)\right]dV\]

Soit sous forme vectorielle:

forme conservative du bilan de quantité de mouvement

\[\frac{\partial\rho\overrightarrow{U}}{\partial t}+\underbrace{div(\rho\overrightarrow{U}\otimes\overrightarrow{U})}_{flux\, convectifs} = \rho\overrightarrow{g}-\underbrace{\overrightarrow{grad}\,\left(p-\lambda div\overrightarrow{U}\right)}_{pression} +\underbrace{div\left(\mu(\nabla\overrightarrow{U}+\nabla^{t}\overrightarrow{U})\right)}_{flux\,visqueux}\]

Que l’on peut écrire sous une forme conservative complète en utilisant le tenseur identité \(\overline{\overline{Id}}\)

\[\underbrace{\frac{\partial\rho\overrightarrow{U}}{\partial t}}_{terme\, instationnaire}+div(\underbrace{\rho\overrightarrow{U}\otimes\overrightarrow{U}}_{terme\, convectif}+\underbrace{(p-\lambda div\overrightarrow{U})}_{pression}\overline{\overline{Id}}\,-\underbrace{\mu(\nabla\overrightarrow{U}+\nabla^{t}\overrightarrow{U})}_{terme\, visqueux})=\rho\overrightarrow{g}\]

2.5.4. loi fondamentale de la dynamique

La loi fondamentale de la dynamique peut s’écrire en terme d’accélération au lieu de quantité de mouvement:

\[m\overrightarrow{\gamma}=\overrightarrow{F}\]

Pour retrouvez cette forme, on va écrire l’équation précédente sous forme non conservative (ou convective) en utilisant le bilan de masse.

Un calcul directe permet de montrez que la variation de la composante suivant x de la quantité de mouvement est bien égale à la masse fois accélération suivant x en utilisant l’équation de bilan de masse:

(2.14)\[\begin{eqnarray} \frac{\Delta \rho u}{\Delta t} & = & \frac{\partial\rho u}{\partial t}+div(\rho u\overrightarrow{U})\\ &=&\rho\left(\frac{\partial u}{\partial t}+\overrightarrow{U}.\overrightarrow{grad}\, u\right) + u \left(\frac{\partial \rho}{\partial t}+ div(\rho\overrightarrow{U})\right)\\ &=& \rho\left(\frac{\partial u}{\partial t}+\overrightarrow{U}.\overrightarrow{grad}\, u\right) = \rho\frac{Du}{Dt} \end{eqnarray}\]

que l’on généralise pour obtenir

(2.15)\[\begin{eqnarray} \frac{\Delta \rho \overrightarrow{U}}{\Delta t} &=& \frac{\partial\rho\overrightarrow{U}}{\partial t}+div(\rho\overrightarrow{U}\otimes\overrightarrow{U})\\ &=& \rho\left(\frac{\partial\overrightarrow{U}}{\partial t}+\overrightarrow{U}.\overrightarrow{grad}\,\overrightarrow{U}\right)\\ &=&\rho \frac{D \overrightarrow{U}}{D t} \end{eqnarray}\]

La forme lagrangienne du bilan de quantité de mouvement s’écrit alors:

forme lagrangienne du principe de la dynamique

\[\rho\underbrace{\left(\frac{\partial\overrightarrow{U}}{\partial t}+\overrightarrow{U}.\overrightarrow{grad}\,\overrightarrow{U}\right)}_{accelération} = \underbrace{\rho\overrightarrow{g}+\overrightarrow{grad}\left(-p+\lambda div\overrightarrow{U}\right)+div\left(\mu(\nabla\overrightarrow{U}+\nabla^{t}\overrightarrow{U})\right)}_{forces\,appliquées}\]

2.5.5. bilan d’énergie cinétique

De cette dernière équation, on peut en déduire une équation de bilan sur l’énergie cinétique \(\frac{1}{2}\rho U^{2}\) en effectuant le produit scalaire avec le vecteur vitesse \(\overrightarrow{U}\)

(2.16)\[\begin{eqnarray} \rho\frac{D\overrightarrow{U}}{Dt}.\overrightarrow{U} &=& \underbrace{\rho\frac{D(\frac{U^{2}}{2})}{Dt}}_{\Delta\,énergie\, cinétique}\\ &=&\underbrace{\rho\overrightarrow{g}.\overrightarrow{U}}_{travail\, gravité} + \underbrace{\overrightarrow{U}.\overrightarrow{grad}\left(-p\right)}_{travail\,de\,la\, pression} \\ &+&\underbrace{\overrightarrow{U}.\overrightarrow{grad}\left(\lambda div\overrightarrow{U}\right)+\overrightarrow{U}.div\left(\mu(\nabla\overrightarrow{U}+\nabla^{t}\overrightarrow{U})\right)}_{dissipation\, visqueuse} \end{eqnarray}\]

2.5.6. équation de Bernoulli

Dans le cas d’un écoulement incompressible stationnaire non visqueux, ce bilan s’écrit:

\[ \rho\overrightarrow{U}.\overrightarrow{grad} \frac{U^{2}}{2} = \rho\overrightarrow{U}.\overrightarrow{grad}(-gz) + \overrightarrow{U}.\overrightarrow{grad}(-p) \]

d’où l’on déduit puisque \(\rho\) est constant:

\[\overrightarrow{U}.\overrightarrow{grad}\left(\rho\frac{U^{2}}{2} + p + \rho g z \right) = 0 \]

qui traduit le fait que la quantité:

\[ \rho\frac{U^{2}}{2} + p + \rho g z \]

est constante le long d’une ligne de courant. C’est le célèbre théorème de Bernoulli qui traduit la conservation de l’énergie mécanique, somme de l’énergie cinétique \(\rho\frac{U^{2}}{2}\) de l’énergie potentiel de gravité \(\rho g z\) et du travail des forces de pression \(p\) le long d’une ligne de courant pour un écoulement incompressible stationnaire non visqueux.

Prudence

Attention dans le cas générale, la constante peut varier d’une ligne de courant à l’autre.

Par contre si le champ de vitesse est irrotationnelle \(\overrightarrow{rot}(\overrightarrow{U}) = \overrightarrow{0}\), la constante est la même dans tout l’écoulement.

\[ \rho\frac{U^{2}}{2} + p + \rho g z = cste\]

Dans ce cas le champ de vitesse découle alors d’un potentiel \(\phi\) :

\[\overrightarrow{U} = \overrightarrow{grad} \phi\]

Cette relation de Bernoulli est souvent utilisée comme première approximation en écoulement incompressible.

Prudence

Si l’écoulement traverse un système mécanique (pompe, hélice, ;;) qui apporte ou enlève de l’énergie à l’écoulement, on ne peut pas appliquer Bernoulli à travers ce système, même si on peut l’appliquer en amont et en aval. Dans ce cas il faut revenir à un bilan de quantité de mouvement pour tenir compte des forces extérieures exercées sur le fluide.

C’est aussi le cas si on applique au fluide des forces extérieures non conservatives, i.e. qui ne découlent pas d’un potentiel.

2.6. Bilan d’énergie

La dernière équation de bilan traduit un bilan d’énergie régit par les principes de la thermodynamique. Pour les fluides monophasiques étudiés, l’état thermodynamique du système est fonction de deux variables d’états indépendantes: le couple \([\rho,p]\) ou le couple \([\rho,T]\).

Les différentes forme d’énergie (par unité de volume) dans un fluide sont:

• l’énergie cinétique: \(E_c\frac{1}{2}\rho U^{2}\)

• l’énergie interne: \(E\) (associé à l’énergie cinétique interne des molécules)

Le premier principe de la thermodynamique stipule que lors de toute transformation, la variation de l’énergie totale \(E_t=E_c + E\) est égale à la quantité d’énergie échangée avec le milieu extérieur, par transfert thermique (chaleur) et transfert mécanique (travail). L’énergie interne par unité de volume \(E=\rho e\) (où \(e\) est l’énergie interne par unité de masse) est une variable d’état thermodynamique, que l’on peut calculer à partir des deux variables d’état indépendantes, par exemple \(E=E(T,\rho)\). La variation de l’énergie totale est donnée par le premier principe de la thermodynamique:

\[d\,E + d\,E_c=\underbrace{\Delta W}_{\mbox{travail échangé avec l'extérieur}}+\underbrace{\Delta Q}_{\mbox{flux de chaleur}}\]

L’énergie interne étant une variable d’état, sa variation ne dépend donc que de l’état final et initial, et non de la transformation. Par contre, le travail \(\Delta W\) et le flux de chaleur \(\Delta Q\) dépendent de la transformation.

2.6.1. travail des forces appliquées

Le travail échangé avec l’extérieur (transfert ordonné d’énergie) correspond à la somme des travaux des forces appliquées: travail des forces de pression, travail des forces de viscosité, travail de forces de gravité.

\[\Delta W=\underbrace{\Delta W_{g}}_{travail\, gravit\acute{e}}+\underbrace{\Delta W_{p}}_{travail\, pression}+\underbrace{\Delta W_{v}}_{travail\, force\, viscosit\acute{e}}\]

Le travail induit par les forces de pression correspond au travail de la pression exercé sur les faces de l’élément:

\[\delta W_p = \overrightarrow{U}.(-p\overrightarrow{n})\,dS\,dt\]

Le bilan sur toutes les faces donne le travail des forces de pression pendant \(dt\):

\[\Delta W_{p}=-\left(p_{1}\overrightarrow{U_{1}}.\overrightarrow{n_{1}}+p_{2}\overrightarrow{U_{2}}.\overrightarrow{n_{2}}\right)dydz\,dt-\left(p_{3}\overrightarrow{U_{3}}.\overrightarrow{n_{3}}+p_{4}\overrightarrow{U_{4}}.\overrightarrow{n_{4}}\right)dxdz\,dt\]

Le travail élémentaire de la pression s’écrit alors:

\[\Delta W_{p}=-div\left(p\,\overrightarrow{U}\right)\,\,dt\,dV\]

Pour le travail de cisaillement fournit par les forces de viscosité, on trouve :

\[\Delta W_{v}=div(\overline{\overline{\sigma}_{v}}.\overrightarrow{U})\,dt\,dV\]

D’où le travail élémentaire des forces exercées:

\[\Delta W= \left(\rho\overrightarrow{g}.\overrightarrow{U}-div\left(p\,\overrightarrow{U}\right) + div(\overline{\overline{\sigma}_{v}}.\overrightarrow{U}) \right) dt\, dV\]

2.6.2. flux de chaleur

Le flux de chaleur correspond à la diffusion de la chaleur dans le gaz, au rayonnement, et à l’échauffement visqueux. En général ce flux de chaleur est irréversible. Dans le cas d’une transformation réversible (lente), le flux de chaleur est relié à la variation d’entropie \(S\):

\[\Delta Q=T\,dS\]

Le second principe de la thermodynamique établit l’irréversibilité des phénomènes physiques, en particulier lors des échanges thermiques. Il implique, que pour une transformation quelconque:

\[dS\,\geq\frac{\Delta Q}{T}\]

Dans les écoulements étudiés nous ne considérons que la conduction. La loi de Fourier donne le flux de chaleur par conduction à travers une surface \(dS\)

\[\Phi_{c}=-\lambda\,\overrightarrow{grad}\,T.\overrightarrow{n}\, dS\]

Le bilan des flux de chaleur reçu dans le volume élémentaire \(dV\) s’écrit:

\[\begin{split}\begin{aligned} \Delta Q_{c} & =+(\lambda_{1}\overrightarrow{grad}T_{1}.\overrightarrow{n_{1}}+\lambda_{2}\overrightarrow{grad}T_{2}.\overrightarrow{n_{2}})dydz\,dt\\ & +(\lambda_{3}\overrightarrow{grad}T_{3}.\overrightarrow{n_{3}}+\lambda_{4}\overrightarrow{grad}T_{4}.\overrightarrow{n_{4}})dxdz\,dt \end{aligned}\end{split}\]

Soit:

\[\Delta Q_{c}=div(\lambda\overrightarrow{grad}T)\,dt\,dV\]

2.6.3. bilan d’énergie

En introduisant l’énergie totale par unité de masse \(e_t=e+\frac{1}{2}V^{2}\), la variation d’énergie dans le volume de contrôle s’écrit:

\[ d\,E_t = \frac{\Delta \rho e_t}{\Delta t} dV\,dt = \left(\frac{\partial\rho e_t}{\partial t} + div(\rho e_t\overrightarrow{U}) \right) dV\,dt \]

d’où l’on déduit l’équation de bilan d’énergie dans l’élément:

forme convective du bilan d’énergie

\[\frac{\partial\rho e_t}{\partial t}+\underbrace{div((\rho e_t+p)\overrightarrow{U})}_{flux\, d'entalpie\, totale}= \underbrace{\rho\overrightarrow{g}.\overrightarrow{U}}_{travail\,gravité} +\underbrace{div(\overline{\overline{\sigma}}_{v}.\overrightarrow{U})}_{travail\, viscosité}+\underbrace{div(\lambda\overrightarrow{grad}T)}_{conduction}\]

en remarquant que \(h_t=e_t+p/\rho\) représente l’enthalpie totale par unité de masse.

En utilisant la forme convective \(\rho\frac{De_t}{Dt}\) et en retranchant l’équation d’énergie cinétique, on obtiens l’équation sur l’énergie interne \(e\):

forme lagrangienne du 1er principe de thermodynamique

\[\rho\frac{De}{Dt}=\underbrace{-p\, div\overrightarrow{U}}_{travail\, compression}+\underbrace{\overline{\overline{\sigma}}_{v}.\overline{\overline{grad}}\overrightarrow{U}}_{dissipation\, visqueuse>0}+\underbrace{div(\lambda\overrightarrow{grad}T)}_{conduction}\]

qui correspond à l’écriture classique du premier principe en thermodynamique écrit pour l’énergie interne \(E\):

\[ \Delta E = -p\,dV + \delta Q \]

En notant que \(div\overrightarrow{U}=-\frac{1}{\rho}\frac{D\rho}{Dt}\), on peut réécrire l’équation précédente:

\[\rho\frac{De}{Dt}=\frac{p}{\rho}\,\frac{D\rho}{Dt}+\delta Q\,\,\mbox{avec }\delta Q=\underbrace{(\overline{\overline{\sigma}}_{v}.\overline{\overline{grad}}\overrightarrow{U}+div(\lambda\overrightarrow{grad}T))}_{irr\acute{e}versible}\]

Pour une transformation réversible, d’après le premier principe, on a par unité de masse avec \(S\) entropie massique:

\[de=T\, dS - p\,d\frac{1}{\rho}\]

que l’on peut écrire

\[\rho\frac{De}{Dt}=\rho T\,\frac{DS}{Dt}+\frac{p}{\rho}\frac{D\rho}{Dt}\]

D’où l’évolution de \(S\) (second principe): $\(\rho T\,\frac{DS}{Dt}=\delta Q\ge0\)$

2.7. Relations thermodynamiques

Pour clore la modélisation de l’écoulement de fluide, nous avons besoin de relations thermodynamiques, permettant de calculer les variables thermodynamiques en fonction de deux variables d’état indépendantes.

La première relation est l’équation d’état du fluide. Dans le cas d’un gaz parfait, l’équation d’état s’écrit \(P\,V_m = \mathcal{R}T\) en unité molaire, ce qui donne en divisant par la masse molaire, la relation d’état pour un fluide:

\[\frac{p}{\rho}=R\,T\]

avec \(R=\mathcal{R}/M\) où \(\mathcal{R}\) est la constante universelle des gaz parfait \(\mathcal{R}=8,31\, J\, K^{-1}mol^{-1}\) et \(M\) la masse molaire du gaz (en \(kg/mol\)).

Pour un gaz parfait, l’énergie interne \(e\) par unité de masse ne dépend que de la température: \(e=e(T)\) .

En notant \(C_{v}\) la chaleur spécifique à volume constant, on a: \(C_{v}=\left(\frac{\Delta Q}{\Delta T}\right)_{V}\):

\[de=C_{v}\, dT\,\mbox{ avec }\, C_{v}=C_{v}(T)\]

Pour un gaz calorifiquement parfait (air à température usuelle), \(C_{v}\) est constante, d’où l’expression de \(e\)

\[e=C_{v}T=\frac{C_{v}}{R}\frac{p}{\rho}\]

De même pour l’enthalpie \(h\) on obtiens:

\[ h=C_{p}T = \frac{C_p}{R} \frac{p}{\rho} \]

En notant que \(h=e+\dfrac{p}{\rho}\), on en déduit que \(R = C_{p}-C_{v}\), ce qui permet d’écrire \(e\) et \(h\) en fonction d’un seul paramètre thermodynamique: le rapport des chaleurs spécifiques \(\gamma = \dfrac{C_p}{C_v}\) :

\[e=\frac{1}{\gamma-1}\frac{p}{\rho} \mbox{ et } h=\frac{\gamma}{\gamma-1}\frac{p}{\rho}\]

On peut déduire l’expression de l’entropie \(S\) d’un gaz parfait, en utilisant la relation du premier principe pour une petite variation réversible:

\[S=S_{0}+C_{v\,}log(\frac{p}{\rho^{\gamma}})\]

On en déduit que pour un fluide isentropique (i.e. \(S=cste\)), on a \(p/\rho^{\gamma}=cste\)

2.8. Équations pour un fluide Newtonien

Le système d’équations, obtenu à partir des équations de bilans précédentes, est aussi connu sous le nom d’équations de Navier-Stokes générale.

2.8.1. forme conservative

Les équations générales de bilan pour un fluide monophasique newtonien s’écrivent donc sous forme conversative, c.a.d. sous forme de bilan dans un petit élément de volume \(dV\) :

équations de Navier-Stokes sous forme convective (bilan)

1. bilan de masse dans \(dV\)

\[\frac{\partial\rho}{\partial t}+div(\rho\overrightarrow{U})=0\]

2. bilan de quantité de mouvement dans \(dV\)

\[\begin{split}\begin{aligned} \frac{\partial\rho\overrightarrow{U}}{\partial t}+div(\rho\overrightarrow{U}\otimes\overrightarrow{U}) & =\rho\overrightarrow{g}-\overrightarrow{grad}\, p+\overrightarrow{grad}(\lambda div\overrightarrow{U})\\ & +div(\mu(\nabla\overrightarrow{U}+\nabla^{t}\overrightarrow{U}))\end{aligned}\end{split}\]

3. bilan d’énergie dans \(dV\)

\[\begin{split}\begin{aligned} \frac{\partial\rho(e+\frac{1}{2}V^{2})}{\partial t}+div((\rho(e+\frac{1}{2}V^{2})+p)\overrightarrow{U}) & =\rho\overrightarrow{g}.\overrightarrow{U}+div(\overline{\overline{\sigma}}_{v}.\overrightarrow{U})\\ & +div(\lambda\overrightarrow{grad}T)\end{aligned}\end{split}\]

2.8.2. forme non conservative (Lagrange):

On peut aussi écrire ces équations pour une particule fluide, en introduisant la dérivée particulaire \(\frac{D}{Dt}\):

équations de Navier-Stokes sous forme lagrangienne

1. conservation de la masse d’une particule fluide:

\[ \frac{D\rho}{Dt} = -\rho\,div\overrightarrow{U} \]

2. principe fondamentale de la dynamique pour une particule fluide:
   masse x accélération = somme des forces appliquées

\[ \rho\frac{D\overrightarrow{U}}{Dt} = -\overrightarrow{\nabla}p+\rho\overrightarrow{f}+div\left(\mu\left(\nabla\overrightarrow{U}+\nabla^{t}\overrightarrow{U}\right)-\frac{2}{3}\mu\,div\overrightarrow{U}\overline{\overline{Id}}\right) \]

3. premier principe de la thermodynamique pour une particule fluide:

\[ \rho\frac{De}{Dt} = -p\,div\overrightarrow{U}+div\left(k\nabla T\right)+\left(\mu\left(\nabla\overrightarrow{U}+\nabla^{t}\overrightarrow{U}\right)-\frac{2}{3}\mu\,div\overrightarrow{U}\overline{\overline{Id}}\right)\otimes\nabla\overrightarrow{U} \]

2.8.3. relations thermodynamiques (fermeture)

Ces équations donnent l’évolution des quantités décrivant le mouvement d’un fluide, à savoir:

• une variable cinématique: la vitesse \(\overrightarrow{U}\)

• deux variables thermodynamiques indépendantes, p.e. \(\rho\) et \(p\)

Il faut donc ajouter des relations thermodynamiques pour fermer le problème et calculer les autres variables thermodynamiques \(e\) et \(T\)

\[e=\frac{1}{\gamma-1}\frac{p}{\rho}\mbox{ et } T = \frac{p}{\rho\,R}\]

Enfin la transformation doit être thermodynamiquement admissible et vérifiée le 2nd principe

\[dS\ge\frac{\delta Q}{T}\]

2.8.4. remarques importantes

Ce système d’équations générales de la mécanique des fluides est bien connu depuis longtemps, mais il est malheureusement fortement non-linéaire et ne possède aucune approximation linéaire universelle, comme la RDM en mécanique des solides. Mathématiquement, on ne sait pas démontrer l’existence et l’unicité de la solution dans le cas général en 3D. Ce problème fait même partie des défis mathématiques du millénaire posés par l’institut mathématique Clay en 2000. Numériquement, même avec les ordinateurs les plus puissants, on ne sait pas calculer une approximation numérique précise, car les écoulements de fluides peuvent présenter des gammes énormes d’échelles de temps et d’espace, comme sur l’image suivante d’un écoulement turbulent complexe:

Fig. 2.22 écoulement turbulent dans un champ d’éoliennes

Turbulence: les écoulements à grande vitesse peuvent présenter de multiples échelles spatiales et temporelles, avec des interactions non-linéaires complexes.

Pour arriver à faire des prédictions, on a donc besoin de faire des approximations, et c’est l’un des grands enjeux en mécanique des fluides.

Le champ moyen est souvent plus simple, et peut être calculer à l’aide d’approximation, en modélisant par exemple l’effet dissipatif de la turbulence par une viscosité turbulente \(\mu_{t}\).

2.9. Equations d’Euler

Dans certains cas, on peut négliger les effets de viscosité et de transfert thermique par conduction, en considérant un écoulement adiabatique de fluide parfait.

Les équations simplifiées forment le système d’équations d’Euler qui régit les écoulements de gaz parfaits adiabatiques (i.e. dans lesquels on a négligé les effets de viscosité et de transfert de chaleur).

Ce système s’écrit sous forme conservative

\[\begin{split}\begin{aligned} \frac{\partial\rho}{\partial t}+div(\rho\overrightarrow{U}) & = & 0\\ \frac{\partial\rho\overrightarrow{U}}{\partial t}+div(\rho\overrightarrow{U}\otimes\overrightarrow{U}+p\,\overline{\overline{Id}}) & = & 0\\ \frac{\partial}{\partial t}(\rho e+\frac{1}{2}\rho U^{2})+div((\rho e+\frac{1}{2}\rho U^{2}+p)\overrightarrow{U}) & = & 0\end{aligned}\end{split}\]

où \(\overline{\overline{Id}}\) est le tenseur identité

Sous une forme cartésienne indicielle, ces équations deviennent:

\[\begin{split}\begin{aligned} \frac{\partial\rho}{\partial t}+\frac{\partial\rho U_{i}}{\partial x_{i}} & = & 0\\ \frac{\partial\rho U_{j}}{\partial t}+\frac{\partial(\rho U_{j}U_{i}+p\delta_{ij})}{\partial x_{i}} & = & 0\\ \frac{\partial}{\partial t}(\rho e+\frac{1}{2}\rho U^{2})+\frac{\partial(\rho e+\frac{1}{2}\rho U^{2}+p)U_{i}}{\partial x_{i}} & = & 0\end{aligned}\end{split}\]

Pour un écoulement bidimensionnel, elles se développent suivant:

\[\begin{split}\begin{aligned} \frac{\partial\rho}{\partial t}+\frac{\partial\rho u}{\partial x}+\frac{\partial\rho v}{\partial y} & = & 0\\ \frac{\partial\rho u}{\partial t}+\frac{\partial\rho u^{2}}{\partial x}+\frac{\partial\rho uv}{\partial y}+\frac{\partial p}{\partial x} & = & 0\\ \frac{\partial\rho v}{\partial t}+\frac{\partial\rho uv}{\partial x}+\frac{\partial\rho v^{2}}{\partial y}+\frac{\partial p}{\partial y} & = & 0\\ \frac{\partial}{\partial t}(\rho e+\frac{1}{2}\rho(u^{2}+v^{2}))+\frac{\partial(\rho e+\frac{1}{2}\rho(u^{2}+v^{2})+p)u}{\partial x} & +\\ \frac{\partial(\rho e+\frac{1}{2}\rho(u^{2}+v^{2})+p)v}{\partial y} & = & 0\end{aligned}\end{split}\]

Ces 5 (4 en 2D) équations de bilan lient l’évolution des 6 (5 en 2D) propriétés \(\rho,p,e,\overrightarrow{U}\) du gaz. Pour fermer le système, on utilise l’équation d’état du fluide:

\[ e=\frac{1}{\gamma-1}\frac{p}{\rho} \]