Couche limite

2.1. Couche limite#

Marc BUFFAT, Dpt Mécanique, Lyon 1

https://en.wikipedia.org/wiki/Boundary_layer ../../_images/Laminar_boundary_layer.png

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rcParams
rcParams['font.family'] = 'serif'
rcParams['font.size'] = 14

2.1.1. Couche limite#

from IPython.display import YouTubeVideo

YouTubeVideo('GgVCTNCwfQk', width=600, height=400)

2.1.1.1. Fundamentals of Boundary Layers (MIT)#

from IPython.display import IFrame
IFrame("https://techtv.mit.edu/videos/a081da3d343242bd845ab379f72c281c/embed/",width="560",height="315")

\(\newcommand{\D}[1]{\frac{d#1}{dx}} \)

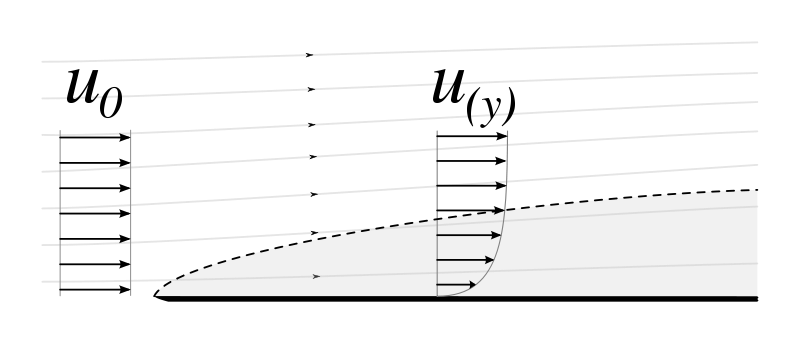
2.1.2. Equation de Blasius#

Avec les hypothèses de couche limite bi-dimensionnelle sans gradient de pression (voir https://en.wikipedia.org/wiki/Blasius_boundary_layer), les composantes de vitesse s’écrivent en fonction de \(\psi(x,y)\), la fonction de courant

\[ u(x,y) = \frac{\partial \psi}{\partial y} \;\; v(x,y) = -\frac{\partial \psi}{\partial x}\]

dont on cherche une forme auto-similaire en éffectuant un changement de variable

2.1.2.1. Recherche d’une solution auto-similaire#

\[ \eta = \frac{y}{\delta(x)} = y \sqrt{\frac{U_0}{\nu x }} \]

solution en fonction de courant \(\psi(x,y)\)

\[ \psi(x,y) = \sqrt{\nu U_0 x} f(\eta) \]

où \(f(\eta)\) est solution de

\[ 2 f''' + f f'' = 0 \]

avec les conditions:

\(f(0)=0\) , \(f'(0)=0\) et \(f''(\infty) = 1 \)

Problème: ce n’est pas une ODE classique, car on a pas 3 conditions initiales !!!

Il faut donc trouvez la condition initiale manquante \(\beta\)

\[f(0)=0 \mbox{ et }f'(0)=0 \mbox{ et } f''(0)=\beta \]

telle que \(f''(\infty) = 1 \)

\(\rightarrow\) résolution numérique par transformation en ODE d’ordre 1

2.1.2.2. ODE d’ordre 3 transformée en 3 ODEs d’ordre 1#

\[\D{Y} = F(Y,t)\]

forme canonique: ODE d’ordre 1

\[\D{Y_1} = Y_2 , \D{Y_2} = Y_3 , \D{Y_3} = -\frac{1}{2}\,Y_1\,Y_3\]

avec les C.L.

\[ Y_1(0)=0 , Y_2(0)=0, Y_3(0)=\beta_0, \mbox{ t.q. }Y_\infty = Y_2(10)=1 \]

### on en déduit la solution autosimilaire fonction de \(f(\eta)\)

\[ \eta = y \sqrt{\frac{U_0}{\nu x }} \]
(2.17)#\[\begin{eqnarray} u(x,y) &=& U_0 f'(\eta) \\ v(x,y) &=& \frac{1}{2} \sqrt{\frac{\nu U_0}{x }}(\eta f'(\eta) - f(\eta)) \end{eqnarray}\]

2.1.2.3. résolution numérique#

Utilisation de solveur classique ODE

from scipy.integrate import odeint

def ODEBlasius(x,Y):
    '''systeme ODE Blasius'''
    dY = np.array([Y[1],Y[2],-0.5*Y[0]*Y[2]])
    return dY
def Blasius(beta0):
    """resoud BLASIUS pour une valeur de beta"""
    Tmax = 10.
    X  = np.linspace(0,Tmax,500)
    Y0 = np.array([0,0,beta0])
    Y  = odeint(ODEBlasius,Y0,X,tfirst=True)
    return X,Y
def ErrBlasius(beta):
    """calcul l'erreur sur la CL en 0"""
    X,Y = Blasius(beta[0])
    err = Y[-1,1] - 1.0
    #print("beta={} err={}".format(Beta[0],err))
    return err

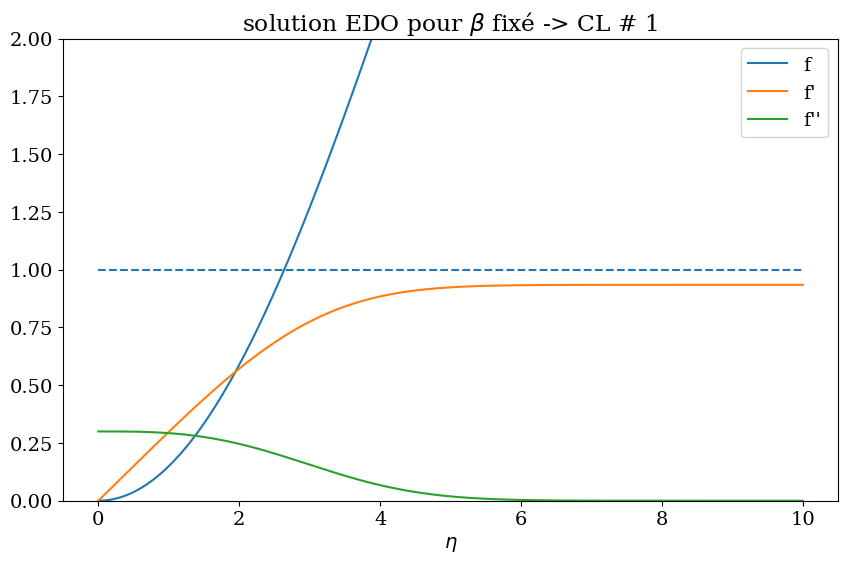
Problème choix de la bonne valeur de \(\beta\)!

# verification pour beta = 0.3
beta0 = 0.3
X,Y = Blasius(beta0)
print("err=",ErrBlasius([beta0]))
plt.figure(figsize=(10,6))
plt.plot(X,Y[:,0],X,Y[:,1],X,Y[:,2])
plt.legend(["f","f'","f''"])
plt.hlines(1.,0,10.,linestyles='--')
plt.ylim([0,2])
plt.xlabel("$\eta$")
plt.title("solution EDO pour $\\beta$ fixé -> CL # 1");

err= -0.06544374655251373
../../_images/b405ea2afac98be3782cc4ec59d5c1ed67b2f666337fa7432b5807ec675490f3.png

2.1.2.4. détermination de la solution par optimisation (racine)#

from scipy.optimize import fsolve

beta_opt= fsolve(ErrBlasius,[beta0],xtol=1.e-12)[0]
print("beta opt=",beta_opt)

beta opt= 0.332057334719411

On retrouve bien l’approximation classique de \(f(\eta)\) pour \(\eta\) petit:

\[ f(\eta) = \frac{1}{2} \beta \eta^2 \mbox{ avec } \beta \approx 0.33205733\]

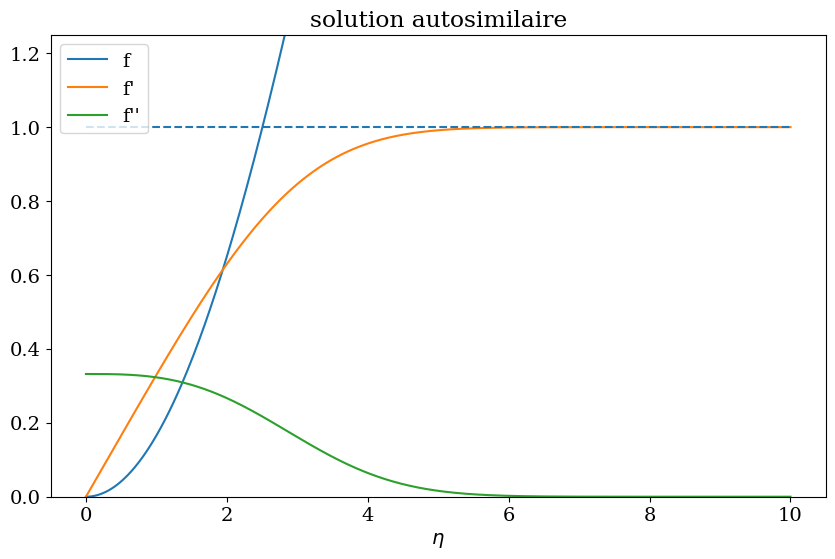
2.1.2.5. tracé de la solution#

X,Y = Blasius(beta_opt)
plt.figure(figsize=(10,6))
plt.plot(X,Y[:,0],X,Y[:,1],X,Y[:,2])
plt.legend(["f","f'","f''"])
plt.xlabel("$\eta$")
plt.hlines(1.,0,10.,linestyles='--')
plt.ylim(0,1.25)
plt.title("solution autosimilaire");
../../_images/90141fd96f0dc51204d95705ee9753fea3d99b3bcd5e3ce50247f9f0f1c22ba5.png 
plt.figure(figsize=(8,6))
plt.plot(Y[:,1],X)
plt.ylim(0,5.)
plt.xlim(0,1.)
plt.xlabel("$U/U_0$")
plt.ylabel("$\eta$")
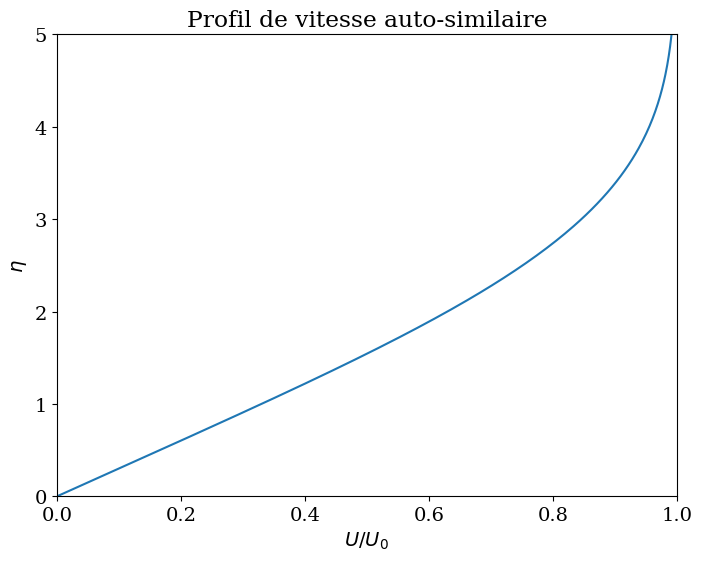
plt.title("Profil de vitesse auto-similaire");
../../_images/ef0c4bed865456ecf3783998c48ec0bb6c2e523afda5bedc69e3eb337cf6ee89.png 
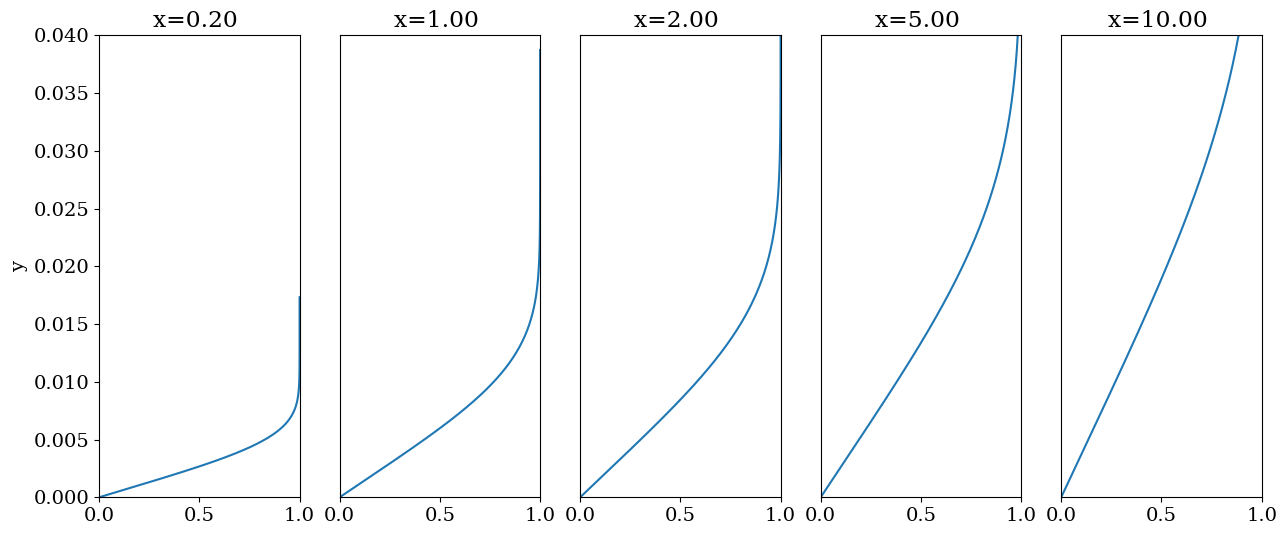
nu = 15e-6
U0 = 1.0
Xp  = np.array([0.2, 1., 2., 5.,10.])
plt.figure(figsize=(15,6))
for k,x in enumerate(Xp):
    eta0 = np.sqrt(U0/(nu*x))
    plt.subplot(1,len(Xp),k+1)
    ax = plt.gca()
    if k>0: 
        ax.get_yaxis().set_visible(False)
    else:
        plt.ylabel("y")
    plt.ylim(0,0.04)
    plt.xlim(0,1.)
    plt.plot(Y[:,1],(X/eta0))
    plt.title("x={:.2f} ".format(x))
../../_images/aa97dfab9b7b591404a253069e0028ff2877b5f43987d6fa06d79fa64131ba16.png 
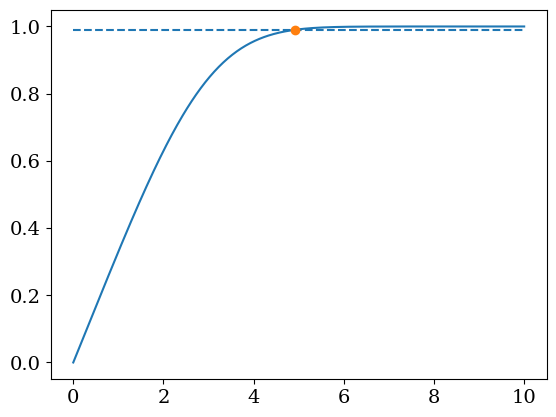
# valeur de eta0 tq V=0.99 U0
i0 = np.abs(Y[:,1]-0.99).argmin()
eta0 = X[i0]
print("eta0=",eta0,Y[i0,1])
plt.plot(X,Y[:,1])
plt.hlines(Y[i0,1],X[0],X[-1],linestyles='dashed')
plt.plot([eta0],[Y[i0,1]],'o')

eta0= 4.909819639278557 0.9899968804588332

[<matplotlib.lines.Line2D at 0x7f9074bfce80>]
../../_images/ec578ee18e1a4034c7cc93107569de5ac6466c57b6d033ad1254fe1308c52834.png 
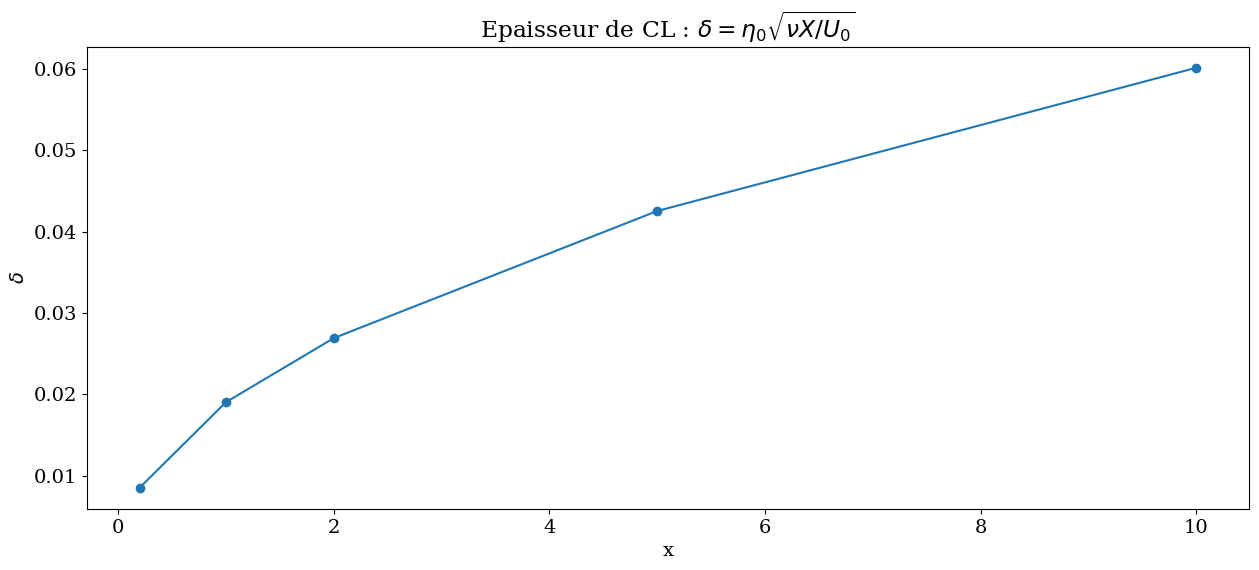
Delta = eta0*np.sqrt(nu*Xp/U0)
plt.figure(figsize=(15,6))
plt.plot(Xp,Delta,'-o')
plt.xlabel("x")
plt.ylabel("$\\delta$")
plt.title("Epaisseur de CL : $\\delta =\eta_0\\sqrt{\\nu X/U_0}$");
../../_images/98675e40e1294e5fc8c4555240d5036753f68132be58cafa8a99512ef9edeaeb.png

2.1.3. Equation de Falkner Scan#

prise en compte d’un gradient de pression avec un champ de vitesse extérieur

\[ u_e(x) = U_0 \left(\frac{x}{L}\right)^m \]

recherche d’une solution auto-similaire

$$ \eta = y \sqrt{\frac{U_0 (m+1)}{2 \nu L}}\left(\frac{x}{L}\right)^{(m-1)/2} $$

on se ramène a résoudre une EDO d’ordre 3

\[ f''' + f f'' + \beta ( 1 - (f')^2) = 0 \]

avec

\[ \beta = \frac{ 2m }{m+1} \]

où m représente l’angle de la plaque / à l’horizontal

  • \(m = 0\) blasius avec une échelle \(\delta = \sqrt{\frac{2\nu x}{U_0}}\)

  • \(m < 0\) adverse pressure gradient

  • \(m > 0\) favorable pressure gradient

2.1.3.1. résolution numérique#

def ODEFalkner(x,Y):
    global BETA
    '''systeme ODE Falkner scan'''
    dY = np.array([Y[1],Y[2],-Y[0]*Y[2] + BETA*(Y[1]**2 - 1.0 )])
    return dY
def Falkner(beta0):
    """resoud Falkner pour une valeur de beta"""
    Tmax = 10.
    X  = np.linspace(0,Tmax,50)
    Y0 = np.array([0,0,beta0])
    Y  = odeint(ODEFalkner,Y0,X,tfirst=True)
    return X,Y
def ErrFalkner(beta):
    """calcul l'erreur sur la CL en 0"""
    X,Y = Falkner(beta[0])
    err = Y[-1,1] - 1.0
    #print("beta={} err={}".format(Beta[0],err))
    return err

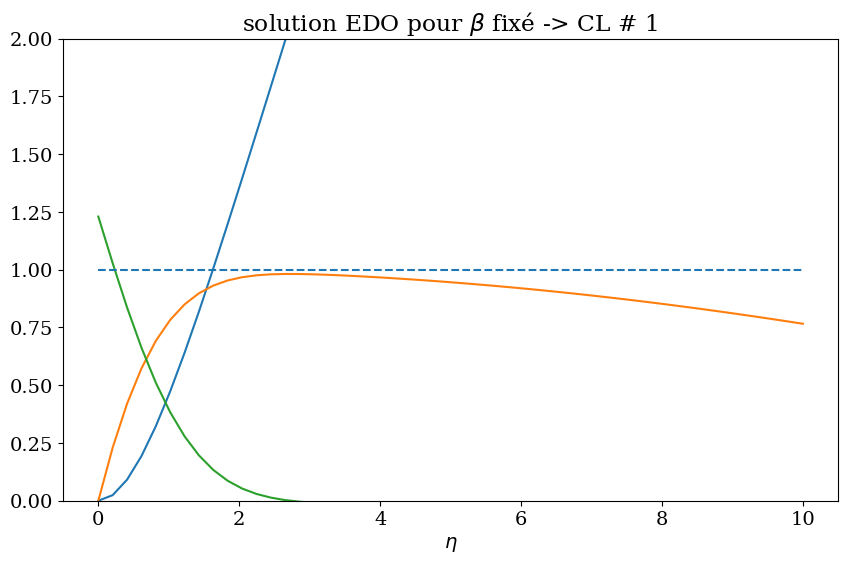
2.1.3.2. gradient de pression favorable m > 0#

m = 1
BETA = 2*m/(m+1)

beta0 = 1.23
X1,Y1 = Falkner(beta0)
print("err=",ErrFalkner([beta0]))
plt.figure(figsize=(10,6))
plt.plot(X1,Y1[:,0],X1,Y1[:,1],X1,Y1[:,2]);
plt.hlines(1.,0,10.,linestyles='--')
plt.ylim([0,2])
plt.xlabel("$\eta$")
plt.title("solution EDO pour $\\beta$ fixé -> CL # 1");

err= -0.23391875896336956
../../_images/1b64c627f10e865a542f1e6d28b8a5eebba46c4cf573e882bc0312a2cba97ffc.png 
beta_opt= fsolve(ErrFalkner,[beta0])[0]
print("beta opt=",beta_opt)

beta opt= 1.2325876845844022

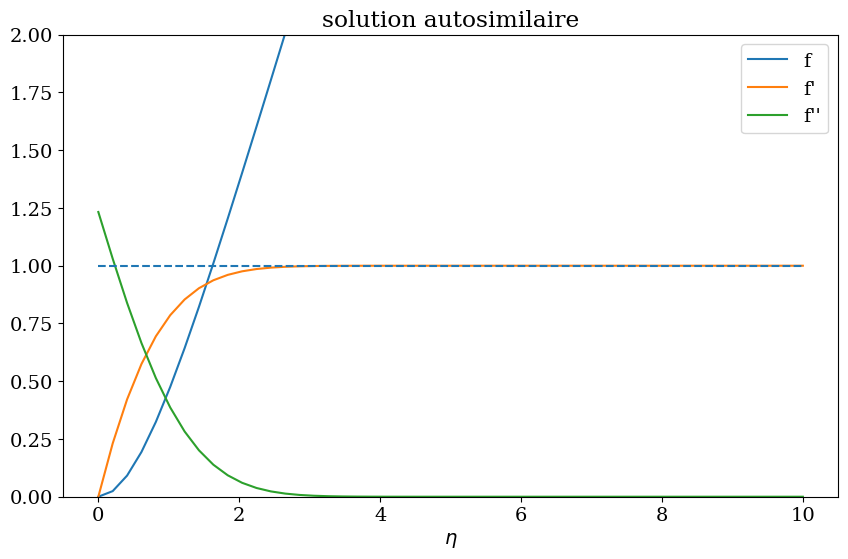
X1,Y1 = Falkner(beta_opt)
plt.figure(figsize=(10,6))
plt.plot(X1,Y1[:,0],X1,Y1[:,1],X1,Y1[:,2])
plt.legend(["f","f'","f''"])
plt.xlabel("$\eta$")
plt.hlines(1.,0,10.,linestyles='--')
plt.ylim(0,2)
plt.title("solution autosimilaire");
../../_images/2979ea30a38c7c7c5bbbd9f850c6208f77d0a8000da6f0301deb2253f1a3b558.png 
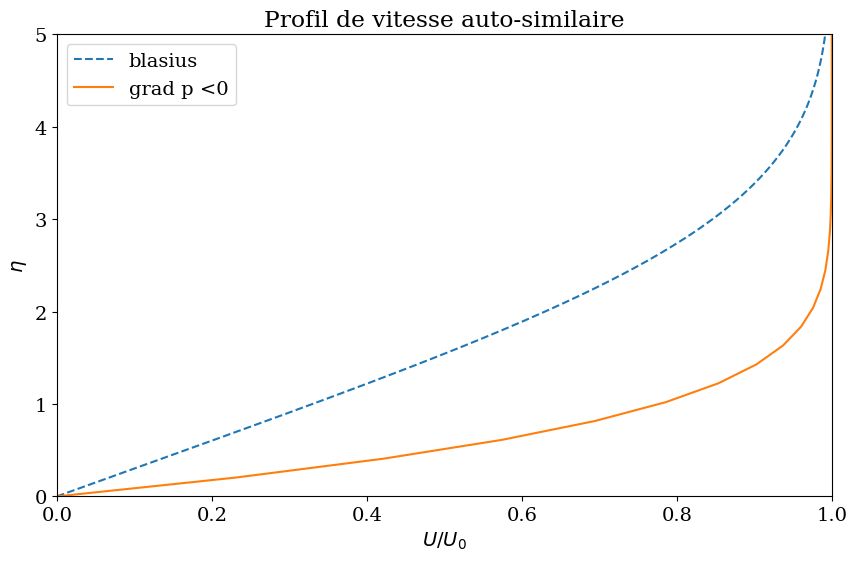
plt.figure(figsize=(10,6))
plt.plot(Y[:,1],X,'--',label="blasius")
plt.plot(Y1[:,1],X1,label="grad p <0")
plt.ylim(0,5.)
plt.xlim(0,1.)
plt.xlabel("$U/U_0$")
plt.ylabel("$\eta$")
plt.legend()
plt.title("Profil de vitesse auto-similaire");
../../_images/e6e666c1678d63e96a3b6bd01a8f5fd2f31b61629d8d27b90e71d6a7f87cc3fe.png

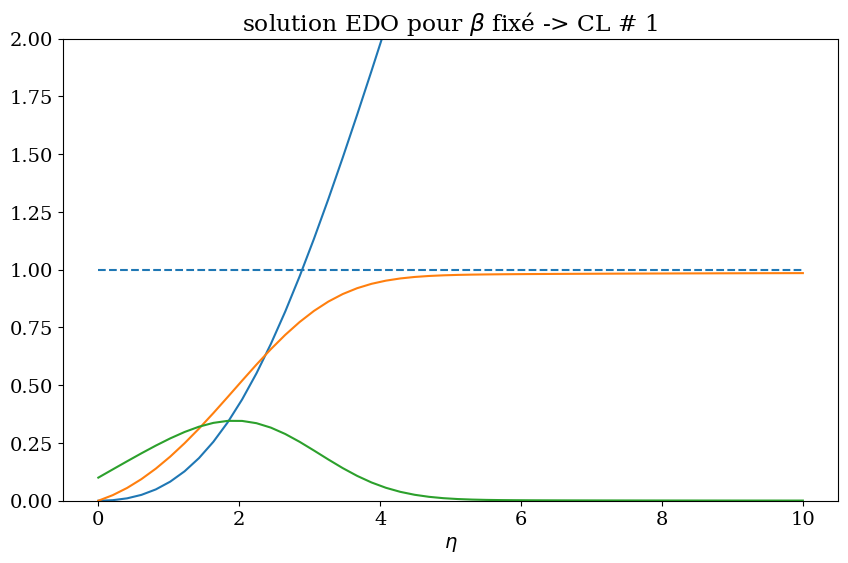
2.1.3.3. gradient de pression adverse#

m = -0.08
BETA = 2*m/(m+1)

beta0 = 0.1
X2,Y2 = Falkner(beta0)
print("err=",ErrFalkner([beta0]))
plt.figure(figsize=(10,6))
plt.plot(X2,Y2[:,0],X2,Y2[:,1],X2,Y2[:,2]);
plt.hlines(1.,0,10.,linestyles='--')
plt.ylim([0,2])
plt.xlabel("$\eta$")
plt.title("solution EDO pour $\\beta$ fixé -> CL # 1");

err= -0.014668533761202918
../../_images/513d533a3121b3786b79629ee3819cb9ccb4ed48e07ef619ffbf9e84515494a5.png 
beta_opt= fsolve(ErrFalkner,[beta0])[0]
print("beta opt=",beta_opt)

beta opt= 0.1497356475032507

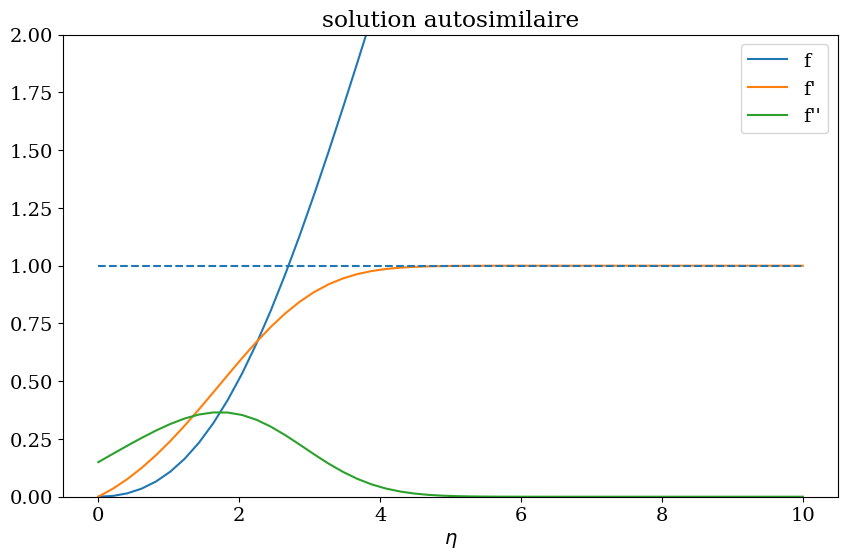
X2,Y2 = Falkner(beta_opt)
plt.figure(figsize=(10,6))
plt.plot(X2,Y2[:,0],X2,Y2[:,1],X2,Y2[:,2])
plt.legend(["f","f'","f''"])
plt.xlabel("$\eta$")
plt.hlines(1.,0,10.,linestyles='--')
plt.ylim(0,2)
plt.title("solution autosimilaire");
../../_images/74bb888639a49b5db22fd388632fed7956ad9607c3ce9c3ac4d7c57a337da23c.png 
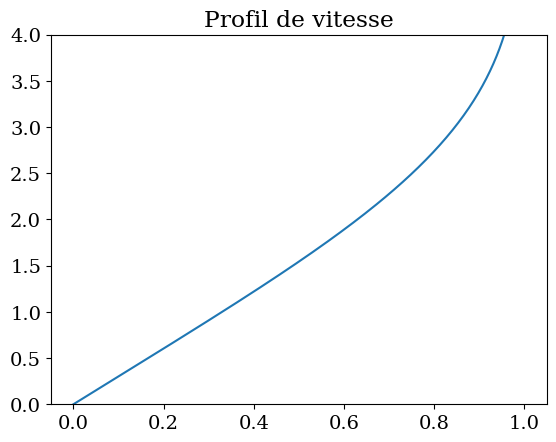
plt.plot(Y[:,1],X)
plt.ylim(0,4)
plt.title("Profil de vitesse");
../../_images/43a2f3990533b32ab3bc105c4e82ffa507d7b4e9f535c63f29ba0d126ff9d1dc.png 
plt.figure(figsize=(10,6))
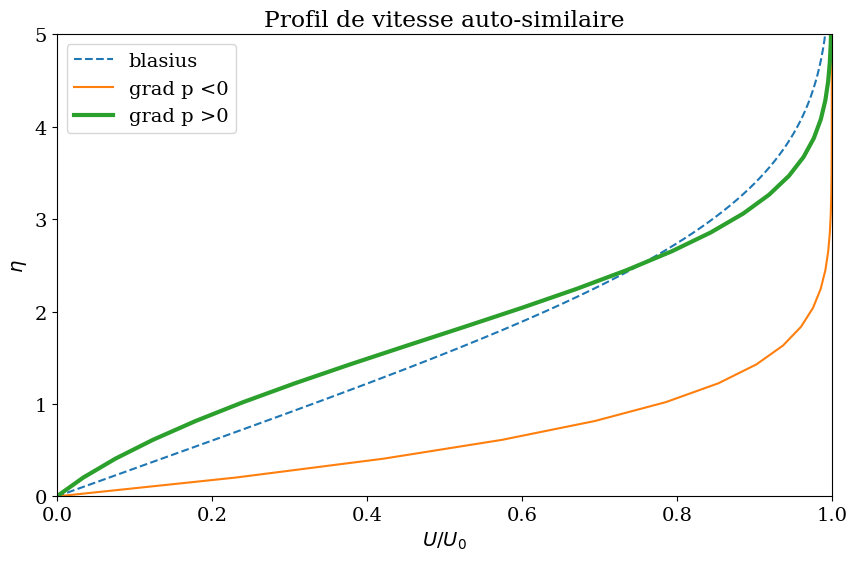
plt.plot(Y[:,1],X,'--',label="blasius")
plt.plot(Y1[:,1],X1,label="grad p <0")
plt.plot(Y2[:,1],X2,lw=3,label="grad p >0")
plt.ylim(0,5.)
plt.xlim(0,1.)
plt.xlabel("$U/U_0$")
plt.ylabel("$\eta$")
plt.legend()
plt.title("Profil de vitesse auto-similaire");
../../_images/f9fe26d798578af40eec460ef3d31c2baa33a264886f382a24f910c0fc548c1f.png

2.1.4. Analyse dimensionnelle#

  1. paramètres : \(U_0\) , \(x\), \(\delta\) , \(\mu\) \(\rho\)

  2. 2 nbres sans dimension: \(Re_x = \frac{\rho U_0 x}{\mu} \gg 1\) et \(\epsilon = \frac{\delta }{x} \ll 1\)$

  • bilan de masse

\[ \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0\]

ordre de grandeur \(V_0\) de v

\[ V_0 = \frac{\delta}{x} U_0 = \epsilon U_0 \]

  • bilan de quantité de mouvement suivant x

\[ \rho u \left(\frac{\partial u}{\partial x} + v \frac{\partial u}{\partial y}\right) = - \frac{\partial p}{\partial x} + \mu \left(\frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} \right) \]

couhe limite laminaire stationnaire sans gradient de pression \(p\approx cste\)

\[ \rho u\frac{\partial u}{\partial x} \approx \rho v\frac{\partial u}{\partial y} \approx \mu \frac{\partial^2 u}{\partial y^2} \]

d’où

\[\rho \frac{U_0^2}{x} \approx \mu \frac{U_0}{\delta ^2}\]

soit $\( \delta^2 = \frac{\mu x}{\rho U_0} \rightarrow \epsilon \approx (Re_x) ^{-1/2}\)$

2.1.5. FIN#

Contenu