Cinématique des fluides

3. Cinématique des fluides#

Marc BUFFAT, dpt mécanique Lyon 1

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
plt.rc('font', family='serif', size='14')
from IPython.display import display
import sympy as sp
import sympy.vector as sv
sp.init_printing()

# bibliothéque de tracé de champ basé sur matplotlib
from validation.Champs import trace_isovaleur, trace_isocol, trace_vecteur, trace_lignes, trajectoire

# système de coordonnées
R = sv.CoordSys3D('R')
display(R)
x = R.x
y = R.y
# parametres
U0,L = sp.symbols("U_0 L",positive=True)
vals = {U0:1, L:1}
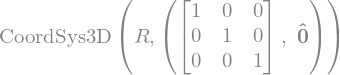
../../_images/dd196fb54af95d21cae7ff64c22fcc67f5487b8e1272d5e18b4c02260e3e7b1f.png

3.1. Champs de vecteur#

On considère maintenant les champs de vecteurs \(\vec{V_1}\) et \(\vec{V_2}\) de composantes dans R

  1. champ V1

\[ \vec{V_1} = U_0 [ \frac{y}{L}, -\frac{x}{L}] \]

  1. champ V2

\[ \vec{V_2} = U_0 [ \sin(\frac{x}{L}), \sin(\frac{y}{L})] \]

questions: pour chacun des champs

  • le champ est-il iso-volume ?

  • le champ est-il rotationnel ?

  • le champ est-il conservatif [1] ?

  • et calcul du potentiel si conservatif

[1] Un champ de vecteurs est dit conservatif si sa circulation sur toute courbe fermée est nulle. Il découlle alors d’un potentiel.

fonctions sympy.vector:

  • sv.divergence()

  • sv.curl()

  • sv.is_conservative()

  • sv.is_solenoidal()

  • sv.scalar_potential()

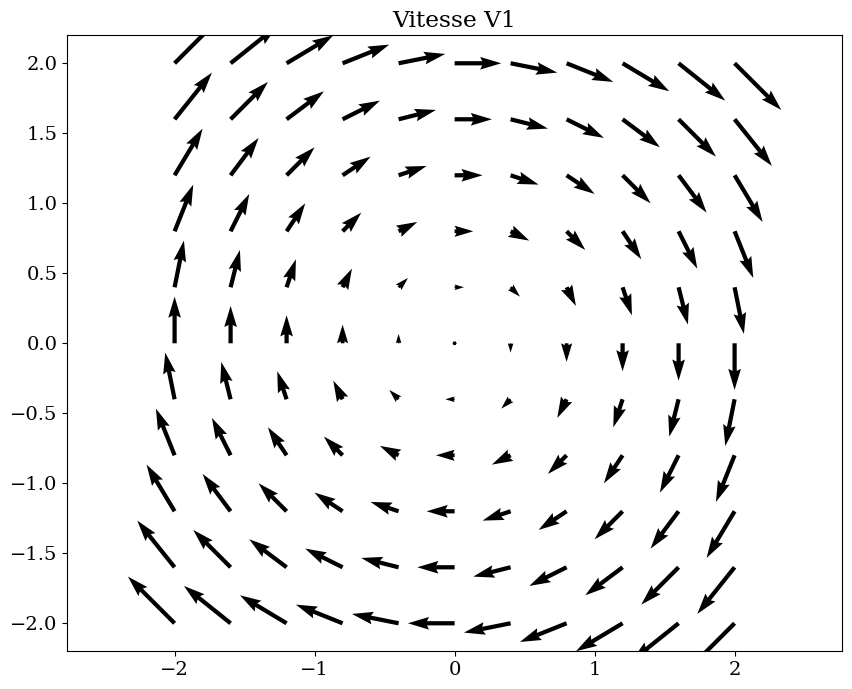
3.1.1. Champ V1#

\[ \vec{V_1} = \frac{U_0}{L}[ y, -x] \]
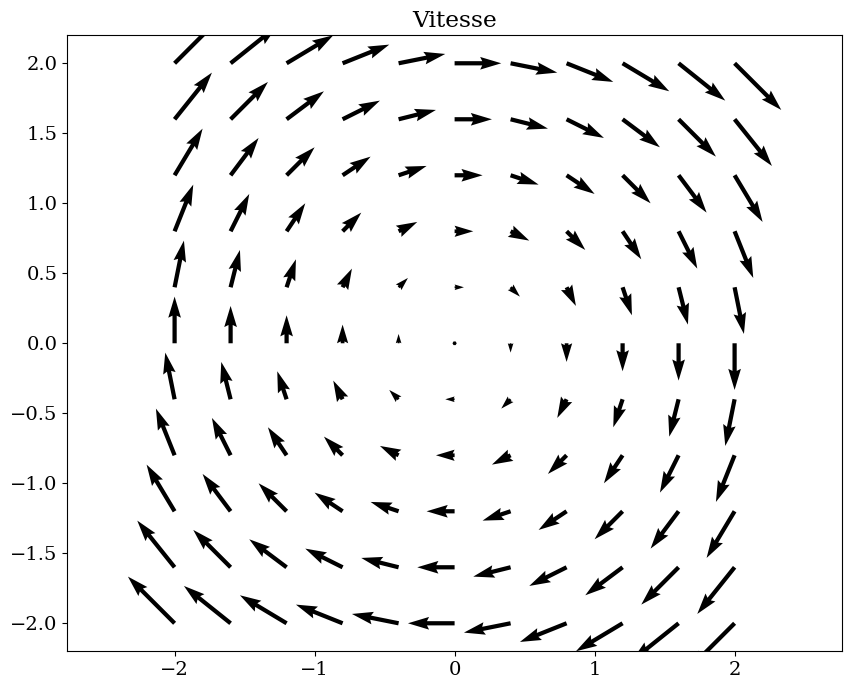
V1 = U0/L*(y*R.i - x*R.j)
display(V1)
plt.figure(figsize=(10,8))
trace_vecteur(V1.subs(vals),R,"Vitesse V1")
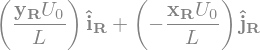
../../_images/592078b8aebe9d5c71c437f9aa8de5959f870f37ddc1789d77369f07ee3a84d9.png ../../_images/feeda687c7a52239688a9574986dfbd9b0def91e6a4c38d127af5d7676f8f539.png 
# calcul la divergence et le rotationnel, test si conservatif et solenoidal
### BEGIN SOLUTION
V1 = (U0/L)*(y*R.i - x*R.j)
display("V1=",V1)
display("divergence de V=",sv.divergence(V1))
display("rotationnel de V=",sv.curl(V1))
print("Champ conservatif:",sv.is_conservative(V1))
print("Champ solenoidal:",sv.is_solenoidal(V1))
### END SOLUTION

'V1='
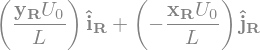
../../_images/592078b8aebe9d5c71c437f9aa8de5959f870f37ddc1789d77369f07ee3a84d9.png 
'divergence de V='
../../_images/702ba12f4bf2cef7092842f0bdd4dc2b8bfdc07d13bc79cc481075cd1cc7c88c.png 
'rotationnel de V='
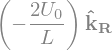
../../_images/e7cad260e1771cfcafdc64bab3154386ffdccf217bc7bba40250db044570faed.png 
Champ conservatif: False
Champ solenoidal: True

plt.figure(figsize=(10,8))
trace_vecteur(V1.subs(vals),R,"V1: Vitesse et lignes de courant")
trace_lignes(V1.subs(vals),R)
../../_images/f67f120887f209e16b1e982362a96592432502755b260624b3d0e68f8d708dcb.png

3.1.2. Champ V2#

\[ \vec{V_2} = U_0 [ \sin(\frac{x}{L}), \sin(\frac{y}{L})] \]
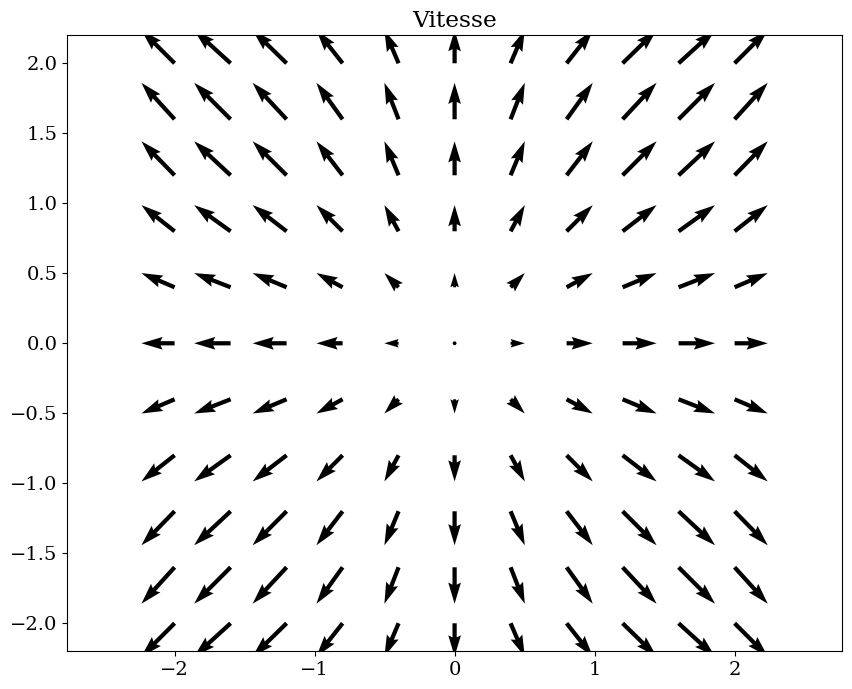
V2 = U0*sp.sin(x/L)*R.i + sp.sin(y/L)*R.j
display(V2)
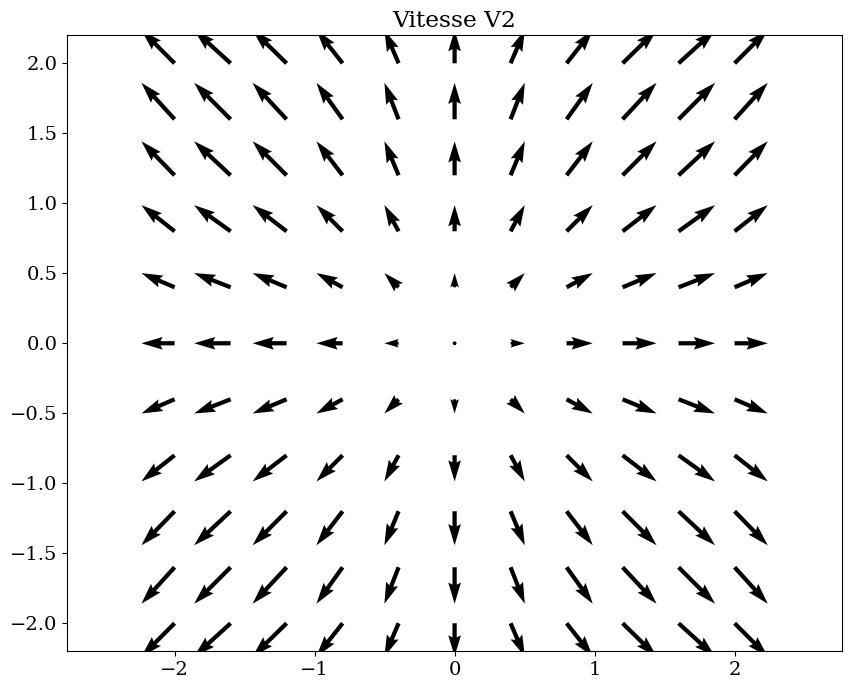
plt.figure(figsize=(10,8))
trace_vecteur(V2.subs(vals),R,"Vitesse V2")
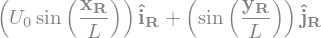
../../_images/b332b1aec1815085ab149b7cfd2442e74196836486539193cb3c0297c931652e.png ../../_images/69a2f33205303297344755424a8324491b45dd9a19ee98b840585c2cbe9a3c34.png 
# calcul la divergence et le rotationnel, test si conservatif et solenoidal
### BEGIN SOLUTION
V2 = U0*sp.sin(x/L)*R.i + sp.sin(y/L)*R.j
display("V2=",V2)
display("divergence de V=",sv.divergence(V2))
display("rotationnel de V=",sv.curl(V2))
print("Champ conservatif:",sv.is_conservative(V2))
print("Champ solenoidal:",sv.is_solenoidal(V2))
psi = sv.scalar_potential(V2,R)
display("potentiel psi=",psi)
### END SOLUTION

'V2='
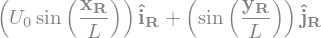
../../_images/b332b1aec1815085ab149b7cfd2442e74196836486539193cb3c0297c931652e.png 
'divergence de V='
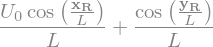
../../_images/4568cfe5e19f2eae57a9722c8e25d04a8a5cdd0e34cd9b3687211a2de3835ad2.png 
'rotationnel de V='
../../_images/9fade945fc7af02493a3648d1d4b1ee92612d3314e1ebd270c58581ddf7922ee.png 
Champ conservatif: True
Champ solenoidal: False

'potentiel psi='
../../_images/b80eb189e9135e133554294f3a56efa0f8dd1cf6ea477822a210b044edb38433.png 
plt.figure(figsize=(10,8))
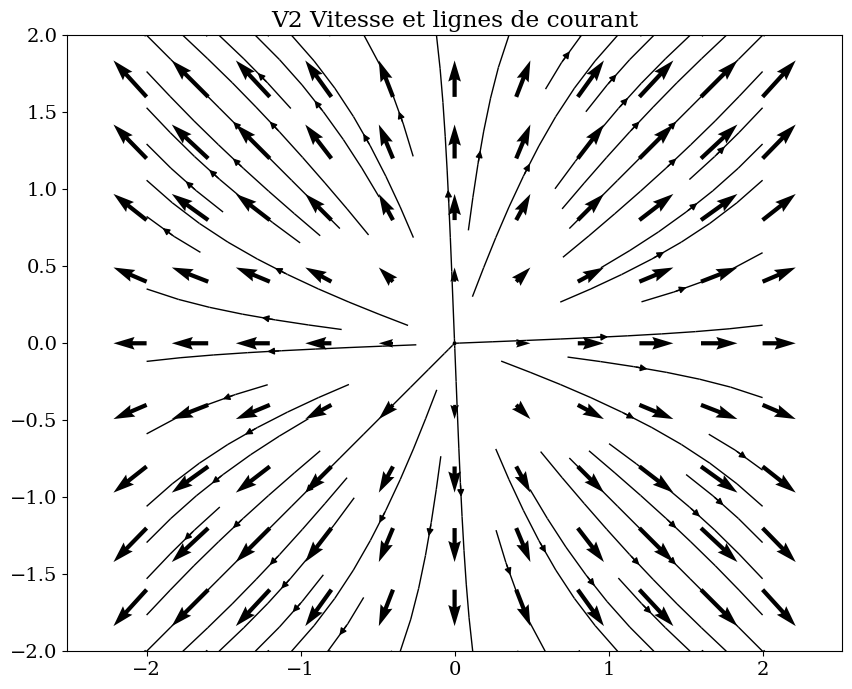
trace_vecteur(V2.subs(vals),R,"V2 Vitesse et lignes de courant")
trace_lignes(V2.subs(vals),R)
../../_images/4f9ebcb1fd454737f8edac02f53d9a0adea9aa691a844a0dca3f5670f7c650c8.png 
plt.figure(figsize=(10,8))
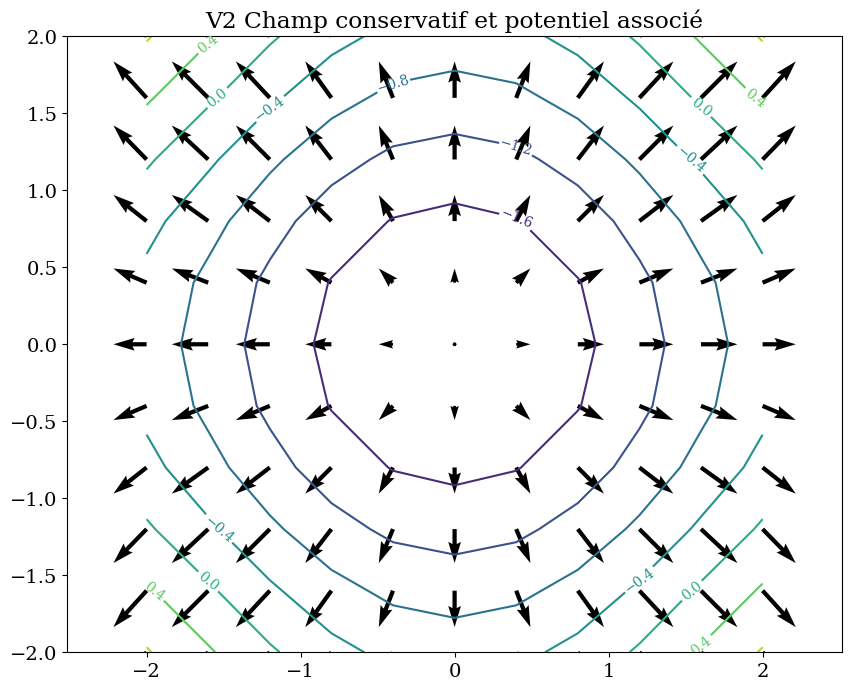
trace_isovaleur(psi.subs(vals),R,"V2 Champ conservatif et potentiel associé")
trace_vecteur(V2.subs(vals),R)
../../_images/1cc9399bc6926961f22c0d0a94c34d3c1c4f734cad7a17b8a0ee375e74638be1.png

3.2. Calcul des trajectoires#

On suppose le champ stationnaire. La trajectoire \(x_p(t),y_p(t)\) d’une particule vérifie:

\[ \frac{d x_p}{dt} = u(x_p(t),y_p(t)) \mbox{ et } \frac{d y_p}{dt} = v(x_p(t),y_p(t)) \]

avec une CI, on se ramène donc à résoudre un système de 2 EDO $\( \dot{Y} = F(Y,t) \mbox{ avec } Y(0) = Y_0\)$

que l’on va résoudre numériquement

3.2.1. application: suivie d’une particule de taille finie#

objectif calcul de la variation de volume de la particule

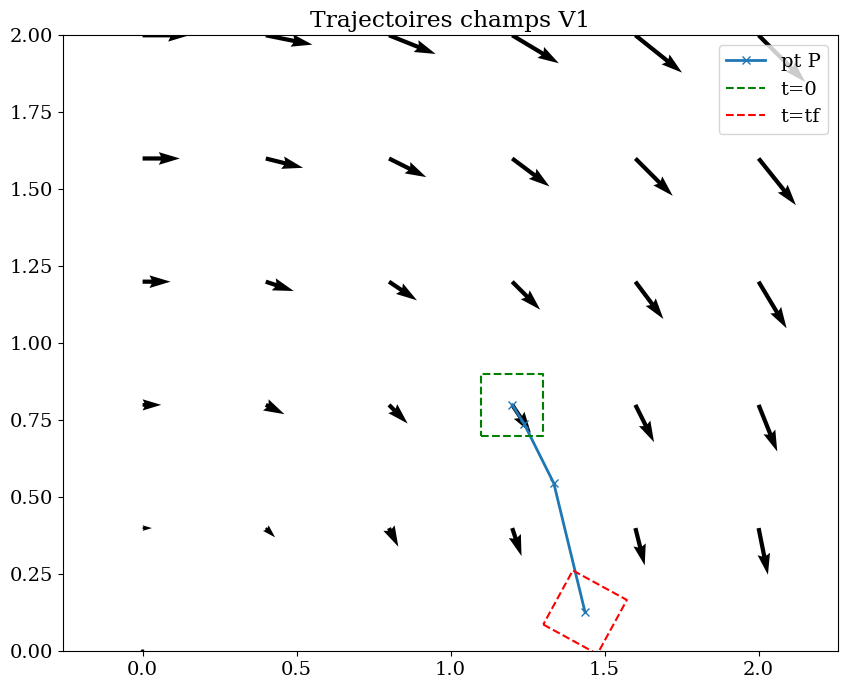
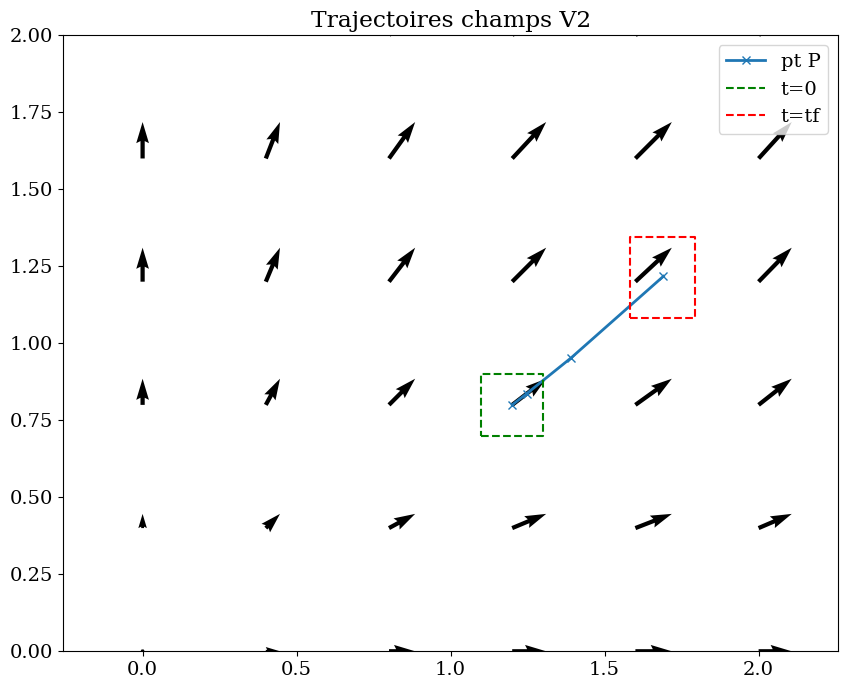
On va ensuite estimer la variation de volume d’une particule, en prenant un petit carré ABCD autour d’un point P et en calculant les trajectoires des 4 points.

On calculera ensuite numériquement la variation relative de volume de la particule, que l’on comparera à la divergence.

\[ \frac{1}{V}\frac{dV}{dt}\]

3.2.2. Champ V1#

\[ \vec{V_1} = \frac{U_0}{L}[ y, -x] \]
V1 = U0/L*(y*R.i - x*R.j)
plt.figure(figsize=(10,8))
trace_vecteur(V1.subs(vals),R,"Vitesse")
../../_images/810ea800e3dae46aac9d05ddead540dfacca53e5d445d88503b32d9340c78cc4.png 
# calcul de la trajectoire des 4 points du carre centre en P de cote 2h pour le champ V1
P = np.array([1.2,0.8])
h = 0.1
TA1, TB1, TC1, TD1, TP1 = 0,0,0,0,0
tt = [0.,0.05,0.2,0.5]
### BEGIN SOLUTION
A = P + [-h,-h]
B = P + [+h,-h]
C = P + [+h,+h]
D = P + [-h,+h]
TA1 = trajectoire(V1.subs(vals),R,A,tt)
TB1 = trajectoire(V1.subs(vals),R,B,tt)
TC1 = trajectoire(V1.subs(vals),R,C,tt)
TD1 = trajectoire(V1.subs(vals),R,D,tt)
TP1 = trajectoire(V1.subs(vals),R,P,tt)
### END SOLUTION

fig = plt.figure(figsize=(10,8))
trace_vecteur(V1.subs(vals),R)
plt.plot(TP1[:,0],TP1[:,1],'-x',label='pt P',lw=2)
plt.plot([TA1[0,0],TB1[0,0],TC1[0,0],TD1[0,0],TA1[0,0]], 
         [TA1[0,1],TB1[0,1],TC1[0,1],TD1[0,1],TA1[0,1]],'--g',label='t=0')
plt.plot([TA1[-1,0],TB1[-1,0],TC1[-1,0],TD1[-1,0],TA1[-1,0]],
         [TA1[-1,1],TB1[-1,1],TC1[-1,1],TD1[-1,1],TA1[-1,1]],'--r',label='t=tf')
plt.xlim(0,2)
plt.ylim(0,2)
plt.title("Trajectoires champs V1")
plt.legend();
../../_images/b63f7eaef6185a5ab34b4387cbe7efe8756e33c152223b7252b4a6fbc9af05f5.png 
# calcul du volume au temp tt[1]
volume1 = 0
dV1 = 0
# fonction calcul du volume a l'instant tt[i]
volume1 = lambda i: np.sqrt(((TB1[i,0]-TA1[i,0])**2+(TB1[i,1]-TA1[i,1])**2)*
                            ((TC1[i,0]-TB1[i,0])**2+(TC1[i,1]-TB1[i,1])**2))
# d'ou la variation de volume: 1/V dV/dt
dV1 = (volume1(1)-volume1(0))/volume1(0)/tt[1]
print("Volume = {:.4f} -> {:.4f}".format(volume1(0),volume1(1)))
print("Variation relative de volume= {:.2f}".format(dV1))
print("Divergence en P= {:.2f}".format(float(sv.divergence(V1))))

Volume = 0.0400 -> 0.0400
Variation relative de volume= 0.00
Divergence en P= 0.00

3.2.3. Champ V2#

\[ \vec{V_2} = U_0 [ \sin(\frac{x}{L}), \sin(\frac{y}{L})] \]
V2 = U0*(sp.sin(x/L)*R.i + sp.sin(y/L)*R.j)
plt.figure(figsize=(10,8))
trace_vecteur(V2.subs(vals),R,"Vitesse")
../../_images/84dffbc93ec2de598f6cfe52ec2e2d2d7d242f61da9902a1cb3f2319220253b8.png 
# calcul de la trajectoire des 4 points du carre centre en P de cote 2h pour le champ V2
TA2, TB2, TC2, TD2 = 0,0,0,0
tt = [0.,0.05,0.2,0.5]
### BEGIN SOLUTION
TA2 = trajectoire(V2.subs(vals),R,A,tt)
TB2 = trajectoire(V2.subs(vals),R,B,tt)
TC2 = trajectoire(V2.subs(vals),R,C,tt)
TD2 = trajectoire(V2.subs(vals),R,D,tt)
TP2 = trajectoire(V2.subs(vals),R,P,tt)
### END SOLUTION

fig = plt.figure(figsize=(10,8))
trace_vecteur(V2.subs(vals),R)
plt.plot(TP2[:,0],TP2[:,1],'-x',label='pt P',lw=2)
plt.plot([TA2[0,0],TB2[0,0],TC2[0,0],TD2[0,0],TA2[0,0]], 
         [TA2[0,1],TB2[0,1],TC2[0,1],TD2[0,1],TA2[0,1]],'--g',label='t=0')
plt.plot([TA2[-1,0],TB2[-1,0],TC2[-1,0],TD2[-1,0],TA2[-1,0]],
         [TA2[-1,1],TB2[-1,1],TC2[-1,1],TD2[-1,1],TA2[-1,1]],'--r',label='t=tf')
plt.xlim(0,2)
plt.ylim(0,2)
plt.title("Trajectoires champs V2")
plt.legend();
../../_images/375bfc5a243b5f0c2f3f55385ca8f322ba5ae3c8aa8705d6aba6ed624ceb9860.png 
### calcul du volume au temp tt[1]
dV2 = 0
volume2 = 0
# calcul du volume a l'instant tt[i]
volume2 = lambda i: np.sqrt(((TB2[i,0]-TA2[i,0])**2+(TB2[i,1]-TA2[i,1])**2)*
                            ((TC2[i,0]-TB2[i,0])**2+(TC2[i,1]-TB2[i,1])**2))
# d'ou la variation de volume: 1/V dV/dt
dV2 = (volume2(1)-volume2(0))/volume2(0)/tt[1]
print("Volume = {:.4f} -> {:.4f}".format(volume2(0),volume2(1)))
print("Variation relative de volume= {:.2f}".format(dV2))
print("Divergence en P= {:.2f}".format(sv.divergence(V2).subs(vals).subs([(R.x,TP2[0,0]),(R.y,TP2[0,1])])))

Volume = 0.0400 -> 0.0421
Variation relative de volume= 1.05
Divergence en P= 1.06

3.3. Mouvement d’une particule dans un champ#

Pour analyser le mouvement, on va calculer l’évolution du champ de vitesse entre 2 points M et M” :

(3.1)#\[\begin{equation} \overrightarrow{U}_{M'}=\overrightarrow{U}_{M}+\overline{\overline{grad}}(\overrightarrow{U})\,\overrightarrow{MM'} \end{equation}\]

En décomposant le gradient de vitesse en une partie symétrique \(\overline{\overline{D}} \; \overrightarrow{MM'}\) et antisymétrique \(\overrightarrow{\Omega}\wedge\overrightarrow{MM'}\)

(3.2)#\[\begin{equation} \overrightarrow{U}_{M'}=\underbrace{\overrightarrow{U}_{M}}_{\mbox{translation}}+\underbrace{\overrightarrow{\Omega}\wedge\overrightarrow{MM'}}_{\mbox{rotation}}+\underbrace{\overline{\overline{D}} \; \overrightarrow{MM'}}_{\mbox{déformation}} \end{equation}\]

où \(\overrightarrow{\Omega}=\frac{1}{2}\overrightarrow{rot}\,\overrightarrow{U}\) est le vecteur tourbillon et \(\overline{\overline{D}} \; \overrightarrow{MM'}\) la vitesse de déformation

On écrit une fonction Gradient(v) qui calcule la matrice gradient du champ V

Pour chaque champ:

  • calcule le gradient

  • calcule la vorticité \(\Omega\)

  • calcule la matrice de déformation \(D\)

def Gradient(v):
    '''calcul matrice gradient du champ de vecteurs v'''
    dv1 = sv.gradient(v.dot(R.i))
    dv2 = sv.gradient(v.dot(R.j))
    dv  = sp.Matrix([[dv1.dot(R.i),dv1.dot(R.j)],[dv2.dot(R.i),dv2.dot(R.j)]])
    return dv

# calcul du gradient de V1 et V2
GradV1 = 0
GradV2 = 0
### BEGIN SOLUTION
GradV2=Gradient(V2)
GradV1=Gradient(V1)
display("Grad V1=",GradV1)
display("Grad V2=",GradV2)
### END SOLUTION

'Grad V1='
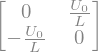
../../_images/bb0063393f145694988ef5632b92481b5351e158980002971f75bc0adadbb4a0.png 
'Grad V2='
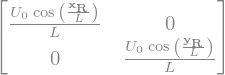
../../_images/ccd9877eb43e9864eb4b43b61c98fd2090ae3d019063f907980d8246716ccde7.png 
# calcul de la vorticité de V1 et V2
Omega1 = 0
Omega2 = 0
### BEGIN SOLUTION
Omega1 = sv.curl(V1)/2
Omega2 = sv.curl(V2)/2
display("Omega1=",Omega1)
display("Omega2=",Omega2)
### END SOLUTION

'Omega1='
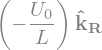
../../_images/ece4a51ee381a9f0bd62c2d88b166e20887986b46305deab2bab64c07434f7b3.png 
'Omega2='
../../_images/9fade945fc7af02493a3648d1d4b1ee92612d3314e1ebd270c58581ddf7922ee.png 
# calcul de la matrice de déformation
D1 = 0
D2 = 0
### BEGIN SOLUTION
D1 = (GradV1+GradV1.transpose())/2
D2 = (GradV2+GradV2.transpose())/2
display("D1=",D1)
display("D2=",D2)
### END SOLUTION

'D1='
../../_images/aef43ba7ac8303b7a03ec46cf59cade9a54afd652edd530eb3bea4c686378845.png 
'D2='
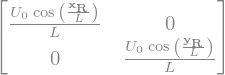
../../_images/ccd9877eb43e9864eb4b43b61c98fd2090ae3d019063f907980d8246716ccde7.png

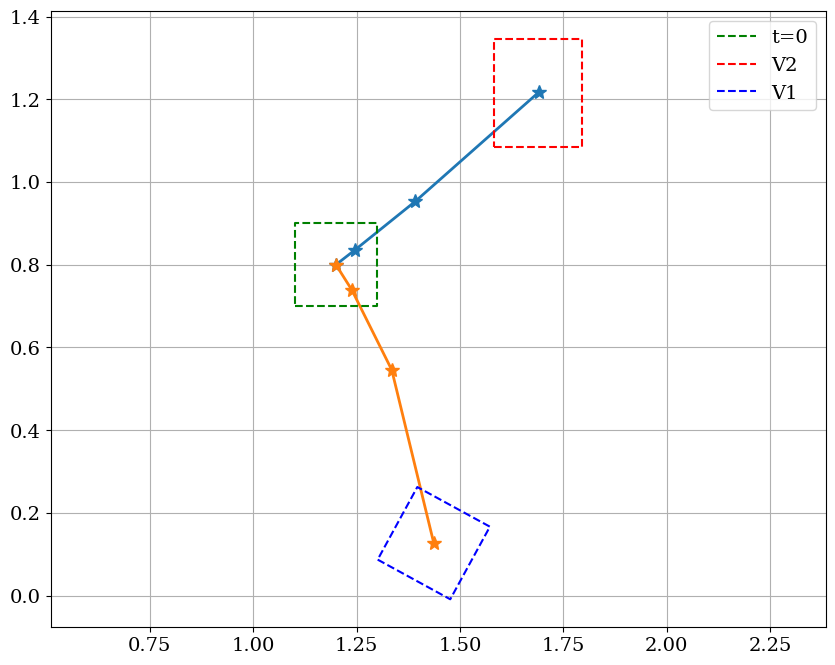
3.4. Trajectoires d’une particule#

  • Tracer les trajectoires des points A,B,C et D partant du meme point P avec les 2 champs

  • Analyser le résultat

plt.figure(figsize=(10,8))
plt.plot(TP2[:,0],TP2[:,1],'-*',lw=2,ms=10)
plt.plot(TP1[:,0],TP1[:,1],'-*',lw=2,ms=10)

plt.plot([TA2[0,0],TB2[0,0],TC2[0,0],TD2[0,0],TA2[0,0]], 
         [TA2[0,1],TB2[0,1],TC2[0,1],TD2[0,1],TA2[0,1]],'--g',label='t=0')
plt.plot([TA2[-1,0],TB2[-1,0],TC2[-1,0],TD2[-1,0],TA2[-1,0]],
         [TA2[-1,1],TB2[-1,1],TC2[-1,1],TD2[-1,1],TA2[-1,1]],'--r',label='V2')
plt.plot([TA1[-1,0],TB1[-1,0],TC1[-1,0],TD1[-1,0],TA1[-1,0]],
         [TA1[-1,1],TB1[-1,1],TC1[-1,1],TD1[-1,1],TA1[-1,1]],'--b',label='V1')
plt.legend()
plt.grid('on')
plt.axis('equal');
../../_images/629581c39ef9baa6ed65fc5136eb74c0b9c500d57ef238068186c6aa1b5865d7.png

3.5. FIN#

Contenu