3. Cinématique des fluides

Marc BUFFAT, dpt mécanique Lyon 1

3.1. Objectifs

Utilisation d’un outil de calcul formel et de calcul numérique pour étudier la cinématique et la dynamique des fluides compressibles, permettant de résoudre complètement le problème.

• application de la démarche du cours

• mise en équation en utilisant du calcul formel pour faciliter les calculs analytiques

• résolution numérique des équations pour obtenir la solution

ATTENTION ces outils ne sont pas une boite noir pour résoudre automatiquement les problèmes. Il faut comprendre la démarche pour pouvoir les utiliser à bon escient.

3.1.1. Environnement Python

Le langage de programmation Python sera utiliser pour manipuler ces outils. Ce n’est pas de la programmation au sens propre, mais l’utilisation d’instructions Python (à la matlab) pour appeler des fonctions. Il faut cependant connaître un minimum de syntaxe du langage Python.

Python est un langage de programmation très générique et utilisé dans beaucoup de contexte différent.

• On écrit chaque instruction sur une ligne et les instructions commencent au début de la ligne (sans espace avant) et se termine par un retour à la ligne

• Python fait la différence entre majuscule et minuscule

• Python encourage une programmation simple et lisible (utilisation des espaces pour aérer l’écriture)

• Python est un langage non-déclaratif (contrairement au C, on ne déclare pas le type des variables)

• Python est un langage interprété (comme matlab): les instructions sont exécutées au fur et à mesure

• Python peut manipuler des nombres réels (float), entier (int), chaînes de caractère (string) (comme le C)

• Mais aussi des listes d’objets (entre [..] [objet1, object2, …]), des tableaux (array) ….

• Python est un langage de programmation généraliste qui utilise intensément des bibliothèques

• Pour cela on utilise la syntaxe: import mabib as nom pour importer la bibliothèque mabib avec un nom simplifié nom

• Nous allons surtout utiliser les modules matplotlib, numpy pour le calcul numérique et sympy pour le calcul symbolique

3.1.2. Notebook IPython

On utilise un serveur web Jupyter avec des notebooks Ipython, qui permet à l’aide d’un simple navigateur web sur un PC, une tablette ou un smartphone d’utiliser ces bibliothèques pythonà distance.

Le notebook est une interface web riche qui permet d’associer du code, la réponse du code et du texte. Le document que l’on travaille est composé de cellules.

• des cellules de code où on tape le code. On clique ensuite sur le bouton > executer pour executer la cellule.

• des cellules de texte Markdown où on rentre du texte qui est ensuite affiché. Il permet d’écrire des équations en utilisant la syntaxe \(\LaTeX\)

ATTENTION en programmation l’ordre d’exécution des instructions est primordiale. Il faut donc exécuter les cellules dans l’ordre en cliquant sur exécuter du début à la fin du notebook et pas en déplaçant avec la souris dans le notebook.

3.1.3. Outils de calcul symbolique et numérique

Utilisation du langage de programmation Python et des notebooks Ipython

Utilisation de bibliothèques python spécialisées en calcul numérique:

• numpy (documentation) (numerical python): pour le calcul numérique avec une manipulation simple de vecteurs et matrices (à la matlab)

• matplotlib: pour le tracer de courbes en 2D

  import numpy as np
  import matplotlib.pyplot as plt
  

et en calcul symbolique:

• sympy symbolic python

• vector bibliothèque sympy pour manipuler des vecteurs et du calcul différentiel

  import sympy as sp
  import sympy.vector as sv
  

Attention en général quand on utilise une fonction d’une bibliothéque python, on préfixe en général la fonction par le nom (simplifié) de la bibliothéque

   np.cos(..)
   sp.cos(..)   
   sp.symbols(..)

np.cos() et sp.cos() sont ils équivalents ?

3.1.4. Bibliothèque vector de sympy

Calcul symbolique sur des champs fonctions des coordonnées d’espace \((x,y,z)\)

import sympy.vector as sv

On définit tout d’abord un système de coordonnées

R = vec.CoordSys3D('R')

qui définit des axes orthogonaux de vecteurs \(\hat{R}.i\) , \(\hat{R}.j\) , \(\hat{R}.k\) (attention notation des vecteurs avec le chapeau \(\hat{}\) au lieu de la flêche \(\vec{}\) )

Les coordonnées sont notées R.x, R.y et R.z

Les opérateurs différentielles classiques sont disponibles:

• opérateur nabla \(\nabla\) appelé Del()

• opérateur rotationnel \(\nabla \times ()\) appelé Curl

• opérateur divergence \(\nabla . ()\) appelé divergence

• opérateur gradient \(\nabla () \) appelé gradient

• test si un champ est conservatif (i.e. irrotationnel) is_conservative()

• test si un champ est solénoidal is_solenoidal

• calcul le potentiel d’un champ conservatif conservative_field()

attention on va manipuler des variables symboliques et des variables numériques. Si on ne fait pas attention, cela peut conduire à des erreurs difficiles à cerner si on change le type d’une variable dans le notebook (c’est possible en Python) !!

On va donc utiliser une convention par defaut: en minuscule les variables symboliques et avec une majuscule les variables numériques

Avec sympy on peut facilement convertir une expression symbolique en fonction python avec la fonction lambdify

• lambdify([a,b,..],expression) définit une fonction python de a,b,.. calculant l’expression

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
plt.rc('font', family='serif', size='14')
from IPython.display import display
import sympy as sp
import sympy.vector as sv
sp.init_printing()

# bibliothéque de tracé de champ basé sur matplotlib
from validation.Champs import trace_isovaleur, trace_isocol, trace_vecteur, trace_lignes, trajectoire

# système de coordonnées
R = sv.CoordSys3D('R')
display(R)
x = R.x
y = R.y

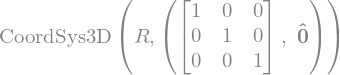
3.2. champ de scalaire

On considère le champ \(\phi(x,y)\) dans le référentiel R

\[ \phi = x^2 + 2y^2\]

On va calculer son gradient et tracer le champ de \(\phi\) et de son gradient:

• fonction sympy.vector: sv.gradient( )

• a priori que doit on obtenir ?

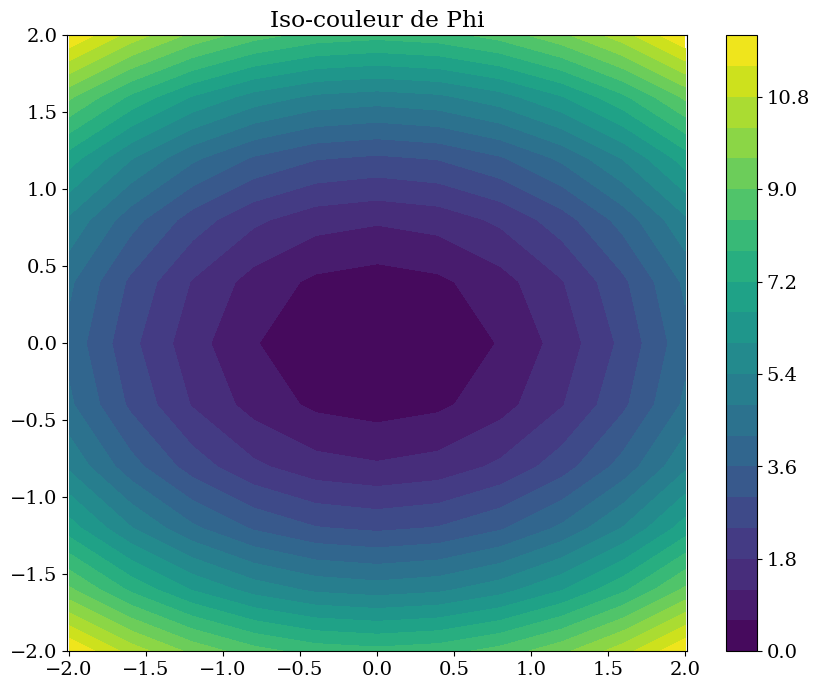
phi = x**2 + 2*y**2
plt.figure(figsize=(10,8))
trace_isocol(phi,R,"Iso-couleur de Phi")

gradphi = 0
### BEGIN SOLUTION
phi = x**2 + 2*y**2
display("phi=",phi)
gradphi = sv.gradient(phi)
display("grad phi=",gradphi)
### END SOLUTION

'phi='

'grad phi='

3.3. Tracé de champs

On va utiliser la bibliothéque matplotlib et la fonction lambdify pour tracer une représentation des champs en calculant les valeurs numériques sur une grille de points. Ces fonctions ont été implémentées dans une bibliothèque locale en Python Champs

On utilise les fonctions suivantes de cette bibliothèque :

• trace_isovaleur(f) trace les isovaleurs de f(x,y)

• trace_vecteur(U) trace le champ de vecteur U(x,y)

• trace_lignes(U) trace les lignes de courant du champ de vecteur U(x,y)

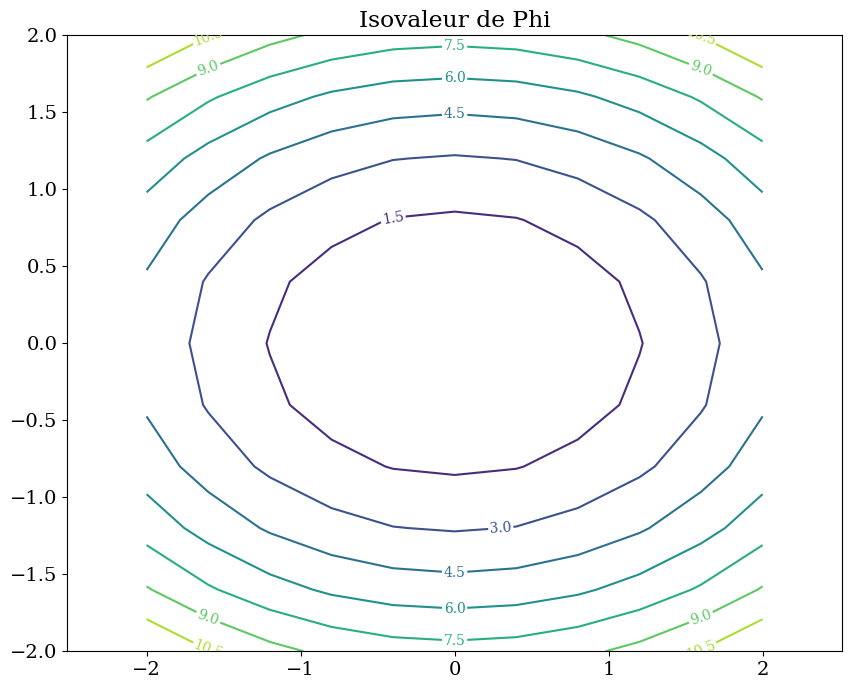
plt.figure(figsize=(10,8))
trace_isovaleur(phi,R,"Isovaleur de Phi")

plt.figure(figsize=(10,8))
trace_vecteur(gradphi,R,"Gradient de phi")

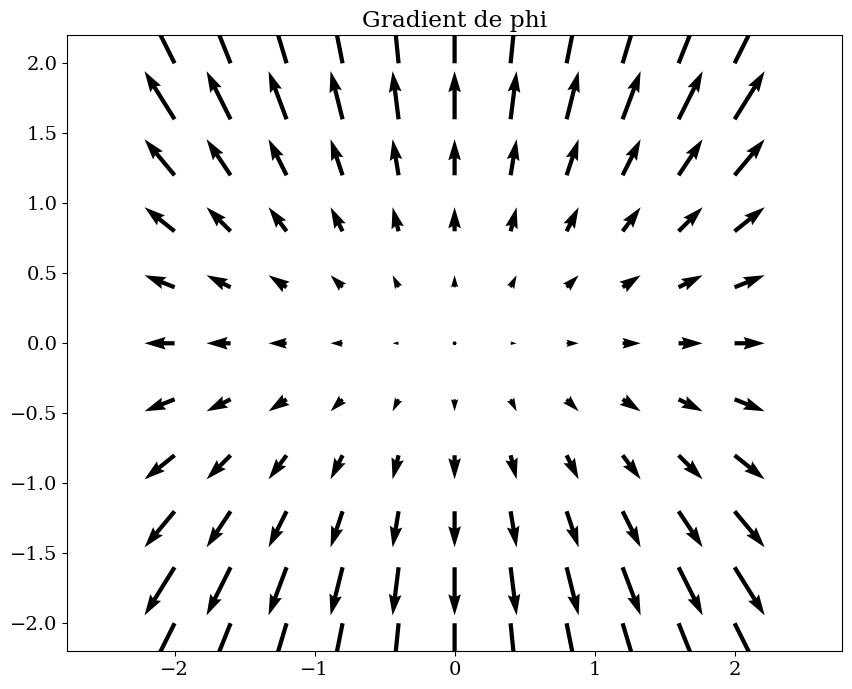
plt.figure(figsize=(10,8))
trace_lignes(gradphi,R,"Ligne de courant")

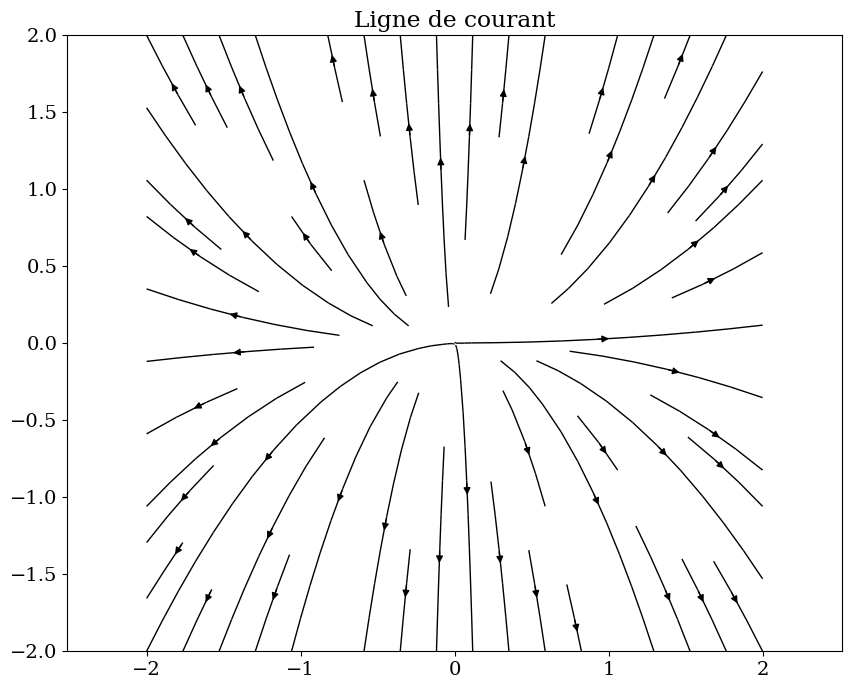
# tracer sur un meme graphique
plt.figure(figsize=(10,8))
trace_isovaleur(phi,R,'Isovaleur, gradient et lignes de $\phi$')
trace_vecteur(gradphi,R)
trace_lignes(gradphi,R)

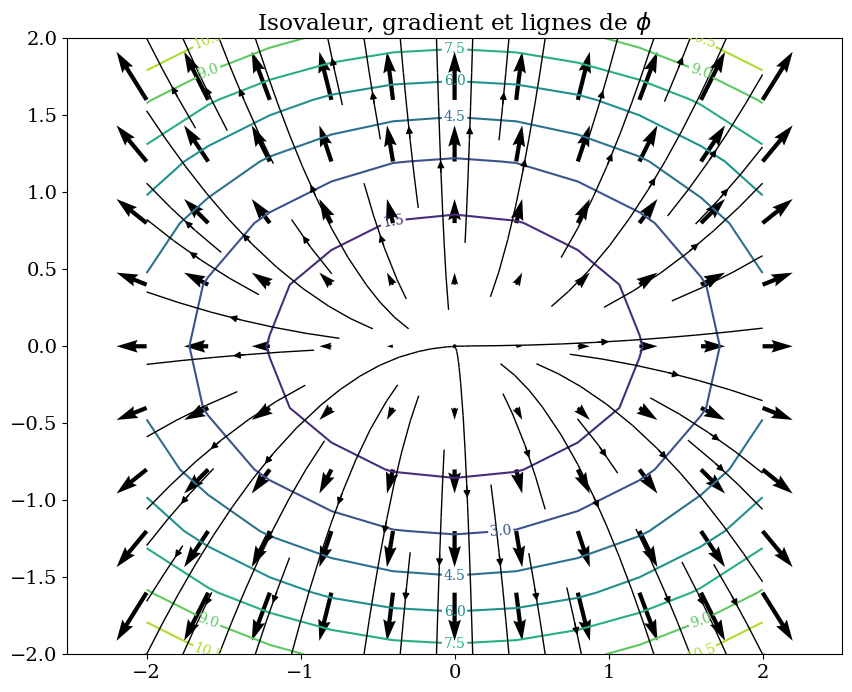
3.4. Champs de vecteur

On considère maintenant les champs de vecteurs \(\vec{V_1}\) et \(\vec{V_2}\) de composantes dans R

1. champ V1

\[ \vec{V_1} = [ y, -x] \]

2. champ V2

\[ \vec{V_2} = [ \sin(x), \sin(y)] \]

questions: pour chacun des champs

• le champ est-il iso-volume ?

• le champ est-il rotationnel ?

• le champ est-il conservatif [1] ?

• et calcul du potentiel si conservatif

[1] Un champ de vecteurs est dit conservatif si sa circulation sur toute courbe fermée est nulle. Il découlle alors d’un potentiel.

fonctions sympy.vector:

• sv.divergence()

• sv.curl()

• sv.is_conservative()

• sv.is_solenoidal()

• sv.scalar_potential()

3.4.1. Champ V1

\[ \vec{V_1} = [ y, -x] \]

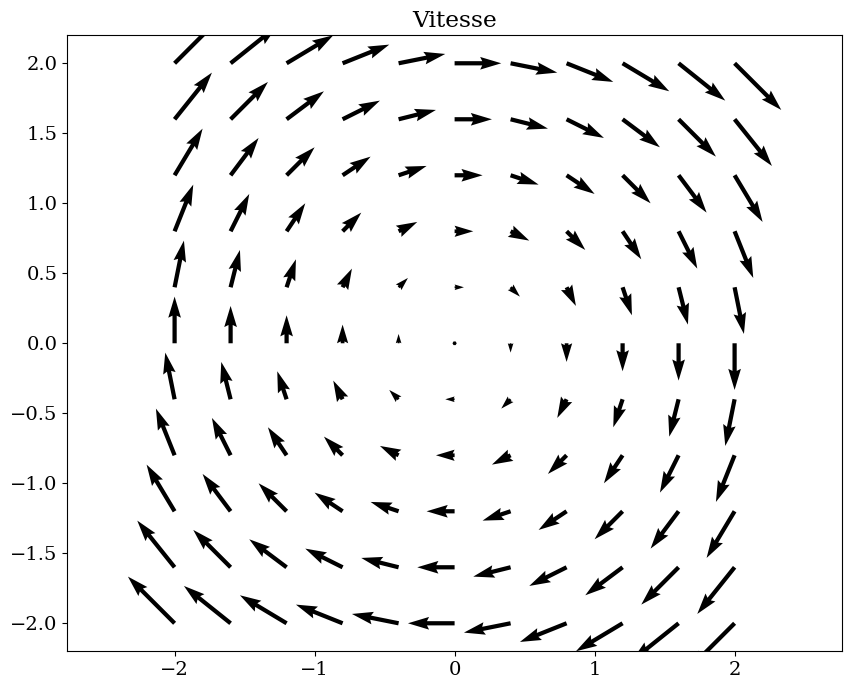
V1 = y*R.i - x*R.j
plt.figure(figsize=(10,8))
trace_vecteur(V1,R,"Vitesse") 

# calcul la divergence et le rotationnel, test si conservatif et solenoidal
### BEGIN SOLUTION
V1 = y*R.i - x*R.j
display("V1=",V1)
display("divergence de V=",sv.divergence(V1))
display("rotationnel de V=",sv.curl(V1))
print("Champ conservatif:",sv.is_conservative(V1))
print("Champ solenoidal:",sv.is_solenoidal(V1))
### END SOLUTION

'V1='

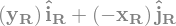
'divergence de V='

'rotationnel de V='

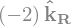
Champ conservatif: False
Champ solenoidal: True

plt.figure(figsize=(10,8))
trace_vecteur(V1,R,"Vitesse et lignes de courant")
trace_lignes(V1,R)

3.4.2. Champ V2

\[ \vec{V_2} = [ \sin(x), \sin(y)] \]

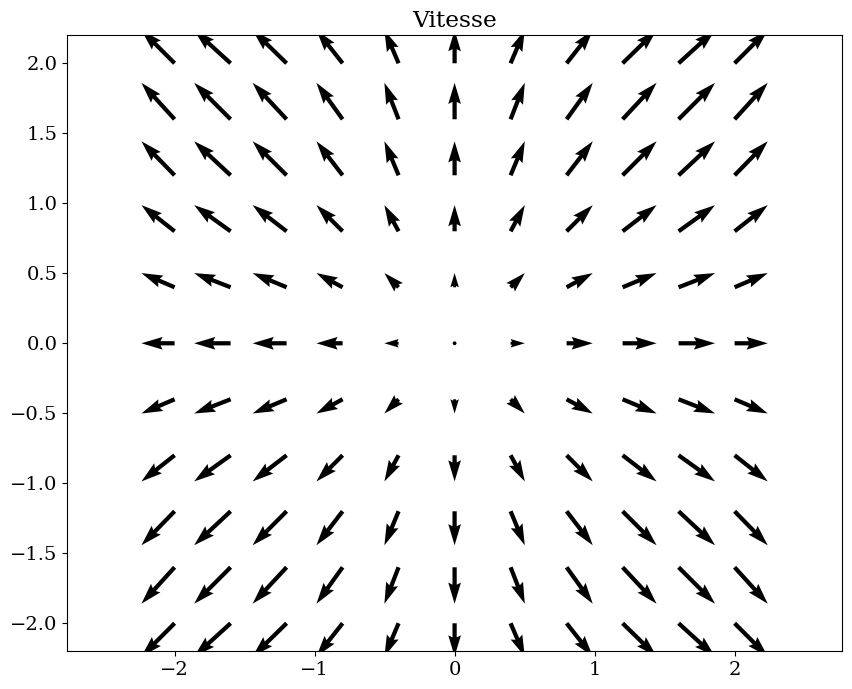
V2 = sp.sin(x)*R.i + sp.sin(y)*R.j
plt.figure(figsize=(10,8))
trace_vecteur(V2,R,"Vitesse")

# calcul la divergence et le rotationnel, test si conservatif et solenoidal
### BEGIN SOLUTION
V2 = sp.sin(x)*R.i + sp.sin(y)*R.j
display("divergence de V=",sv.divergence(V2))
display("rotationnel de V=",sv.curl(V2))
print("Champ conservatif:",sv.is_conservative(V2))
print("Champ solenoidal:",sv.is_solenoidal(V2))
psi = sv.scalar_potential(V2,R)
display("potentiel psi=",psi)
### END SOLUTION

'divergence de V='

'rotationnel de V='

Champ conservatif: True
Champ solenoidal: False

'potentiel psi='

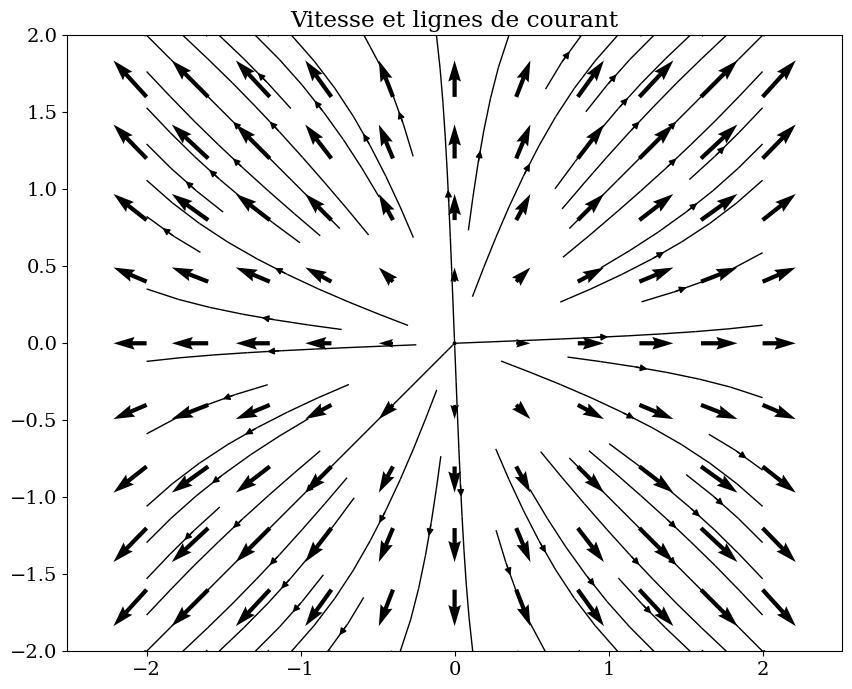
plt.figure(figsize=(10,8))
trace_vecteur(V2,R,"Vitesse et lignes de courant")
trace_lignes(V2,R)

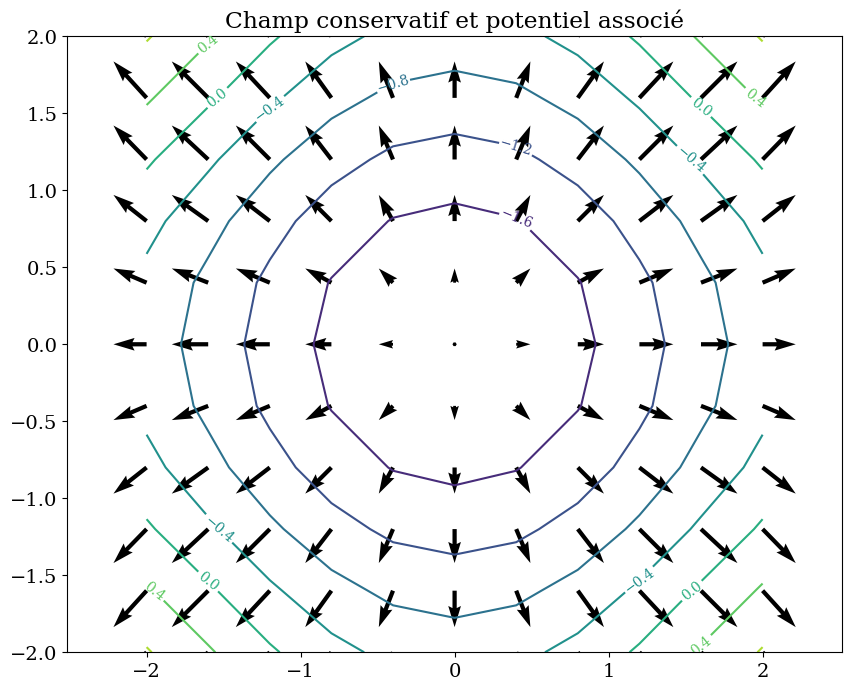
plt.figure(figsize=(10,8))
trace_isovaleur(psi,R,"Champ conservatif et potentiel associé")
trace_vecteur(V2,R)

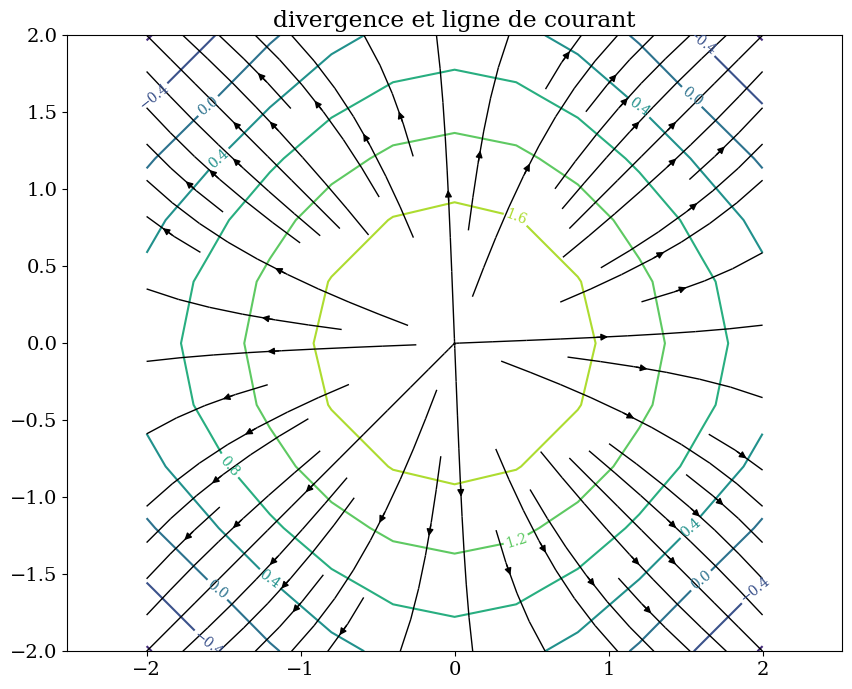
divV2 = sv.divergence(V2)
fig = plt.figure(figsize=(10,8))
trace_isovaleur(divV2,R,"divergence et ligne de courant")
trace_lignes(V2,R)

3.5. Calcul des trajectoires

On suppose le champ stationnaire. La trajectoire \(x_p(t),y_p(t)\) d’une particule vériie:

\[ \frac{d x_p}{dt} = u(x_p(t),y_p(t)) \mbox{ et } \frac{d y_p}{dt} = v(x_p(t),y_p(t)) \]

avec une CI, on se ramène donc à résoudre un système de 2 EDO $\( \dot{Y} = F(Y,t) \mbox{ avec } Y(0) = Y_0\)$

que l’on va résoudre numériquement (avec quelle méthode ?)

3.5.1. application: suivie d’une particule de taille finie

objectif calcul de la variation de volume de la particule

On va ensuite estimer la variation de volume d’une particule, en prenant un petit carré ABCD autour d’un point P et en calculant les trajectoires des 4 points.

On pourra utiliser la fonction trajectoire

• trajectoire(V,R,A,tt) calcul la trajectoire dans le champ de vitesse V dans R, partant du point A pendant les temps tt

On calculera ensuite numeriquement la variation relative de volume de la particule, que l’on comparera à la divergence.

\[ \frac{1}{V}\frac{dV}{dt}\]

On écrirera une fonction volume1(i) pour calculer le volume de la particule à l’instant tt[i] avec le champ V1 et volume2(i) avec le champ V2

3.5.2. Champ V1

\[ \vec{V_1} = [ y, -x] \]

V1 = y*R.i - x*R.j
plt.figure(figsize=(10,8))
trace_vecteur(V1,R,"Vitesse") 

# calcul de la trajectoire des 4 points du carre centre en P de cote 2h pour le champ V1
P = np.array([1.2,0.8])
h = 0.1
TA1, TB1, TC1, TD1, TP1 = 0,0,0,0,0
tt = [0.,0.05,0.2,0.5]
### BEGIN SOLUTION
A = P + [-h,-h]
B = P + [+h,-h]
C = P + [+h,+h]
D = P + [-h,+h]
TA1 = trajectoire(V1,R,A,tt)
TB1 = trajectoire(V1,R,B,tt)
TC1 = trajectoire(V1,R,C,tt)
TD1 = trajectoire(V1,R,D,tt)
TP1 = trajectoire(V1,R,P,tt)
### END SOLUTION

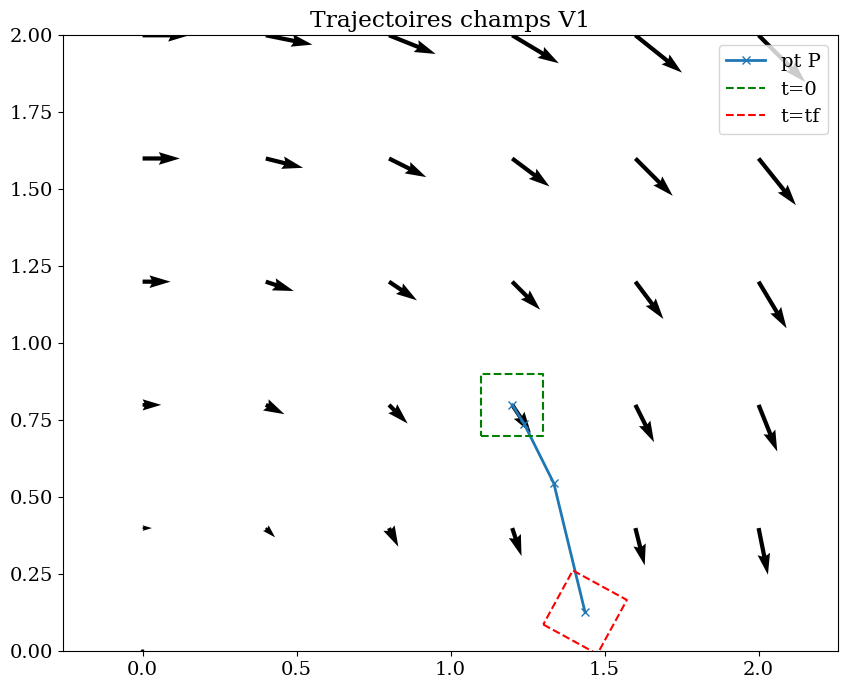
fig = plt.figure(figsize=(10,8))
trace_vecteur(V1,R)
plt.plot(TP1[:,0],TP1[:,1],'-x',label='pt P',lw=2)
plt.plot([TA1[0,0],TB1[0,0],TC1[0,0],TD1[0,0],TA1[0,0]], 
         [TA1[0,1],TB1[0,1],TC1[0,1],TD1[0,1],TA1[0,1]],'--g',label='t=0')
plt.plot([TA1[-1,0],TB1[-1,0],TC1[-1,0],TD1[-1,0],TA1[-1,0]],
         [TA1[-1,1],TB1[-1,1],TC1[-1,1],TD1[-1,1],TA1[-1,1]],'--r',label='t=tf')
plt.xlim(0,2)
plt.ylim(0,2)
plt.title("Trajectoires champs V1")
plt.legend();

# calcul du volume au temp tt[1]
volume1 = 0
dV1 = 0
# fonction calcul du volume a l'instant tt[i]
volume1 = lambda i: np.sqrt(((TB1[i,0]-TA1[i,0])**2+(TB1[i,1]-TA1[i,1])**2)*
                            ((TC1[i,0]-TB1[i,0])**2+(TC1[i,1]-TB1[i,1])**2))
# d'ou la variation de volume: 1/V dV/dt
dV1 = (volume1(1)-volume1(0))/volume1(0)/tt[1]
print("Volume = {:.4f} -> {:.4f}".format(volume1(0),volume1(1)))
print("Variation relative de volume= {:.2f}".format(dV1))
print("Divergence en P= {:.2f}".format(float(sv.divergence(V1))))

Volume = 0.0400 -> 0.0400
Variation relative de volume= 0.00
Divergence en P= 0.00

3.5.3. Champ V2

\[ \vec{V_2} = [ \sin(x), \sin(y)] \]

V2 = sp.sin(x)*R.i + sp.sin(y)*R.j
plt.figure(figsize=(10,8))
trace_vecteur(V2,R,"Vitesse")

# calcul de la trajectoire des 4 points du carre centre en P de cote 2h pour le champ V2
TA2, TB2, TC2, TD2 = 0,0,0,0
tt = [0.,0.05,0.2,0.5]
### BEGIN SOLUTION
TA2 = trajectoire(V2,R,A,tt)
TB2 = trajectoire(V2,R,B,tt)
TC2 = trajectoire(V2,R,C,tt)
TD2 = trajectoire(V2,R,D,tt)
TP2 = trajectoire(V2,R,P,tt)
### END SOLUTION

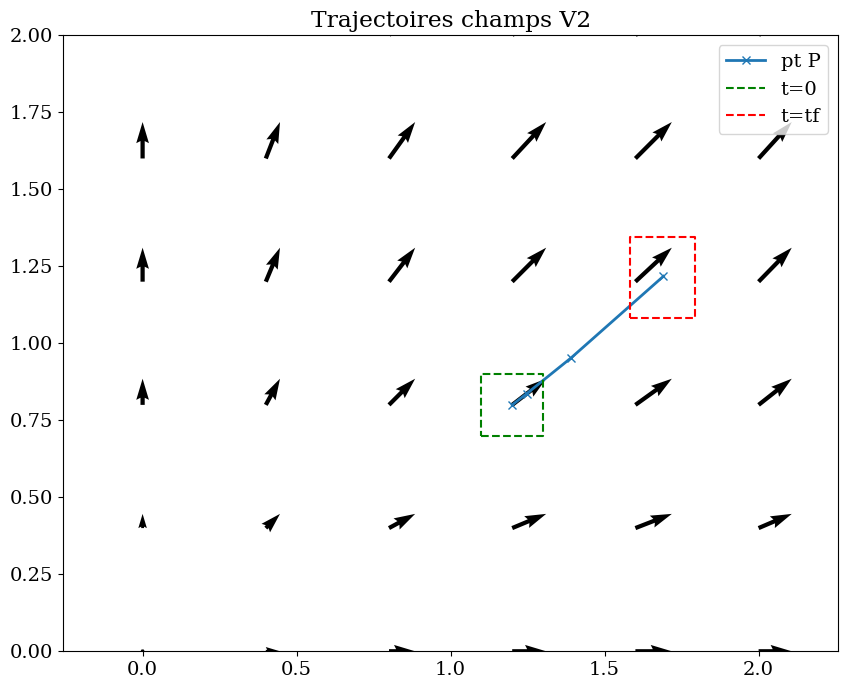
fig = plt.figure(figsize=(10,8))
trace_vecteur(V2,R)
plt.plot(TP2[:,0],TP2[:,1],'-x',label='pt P',lw=2)
plt.plot([TA2[0,0],TB2[0,0],TC2[0,0],TD2[0,0],TA2[0,0]], 
         [TA2[0,1],TB2[0,1],TC2[0,1],TD2[0,1],TA2[0,1]],'--g',label='t=0')
plt.plot([TA2[-1,0],TB2[-1,0],TC2[-1,0],TD2[-1,0],TA2[-1,0]],
         [TA2[-1,1],TB2[-1,1],TC2[-1,1],TD2[-1,1],TA2[-1,1]],'--r',label='t=tf')
plt.xlim(0,2)
plt.ylim(0,2)
plt.title("Trajectoires champs V2")
plt.legend();

### calcul du volume au temp tt[1]
dV2 = 0
volume2 = 0
# calcul du volume a l'instant tt[i]
volume2 = lambda i: np.sqrt(((TB2[i,0]-TA2[i,0])**2+(TB2[i,1]-TA2[i,1])**2)*
                            ((TC2[i,0]-TB2[i,0])**2+(TC2[i,1]-TB2[i,1])**2))
# d'ou la variation de volume: 1/V dV/dt
dV2 = (volume2(1)-volume2(0))/volume2(0)/tt[1]
print("Volume = {:.4f} -> {:.4f}".format(volume2(0),volume2(1)))
print("Variation relative de volume= {:.2f}".format(dV2))
print("Divergence en P= {:.2f}".format(divV2.subs([(R.x,TP2[0,0]),(R.y,TP2[0,1])])))

Volume = 0.0400 -> 0.0421
Variation relative de volume= 1.05
Divergence en P= 1.06

3.6. Mouvement d’une particule dans un champ

Pour analyser le mouvement, on va calculer l’évolution du champ de vitesse entre 2 points M et M” :

(3.1)\[\begin{equation} \overrightarrow{U}_{M'}=\overrightarrow{U}_{M}+\overline{\overline{grad}}(\overrightarrow{U})\,\overrightarrow{MM'} \end{equation}\]

En décomposant le gradient de vitesse en une partie symétrique \(\overrightarrow{D}\) et antisymétrique \(\overrightarrow{\Omega}\wedge\overrightarrow{MM'}\)

(3.2)\[\begin{equation} \overrightarrow{U}_{M'}=\underbrace{\overrightarrow{U}_{M}}_{\mbox{translation}}+\underbrace{\overrightarrow{\Omega}\wedge\overrightarrow{MM'}}_{\mbox{rotation}}+\underbrace{\overrightarrow{D}}_{\mbox{déformation}} \end{equation}\]

où \(\overrightarrow{\Omega}=\frac{1}{2}\overrightarrow{rot}\,\overrightarrow{U}\) est le vecteur tourbillon et \(\overrightarrow{D}\) la vitesse de déformation

Ecrire une fonction Gradient(v) qui calcule la matrice gradient du champ V

questions pour chaque champ

• calculer le gradient

• calculer la vorticité \(\Omega\)

• calculer la matrice de déformation \(D\)

def Gradient(v):
    '''calcul matrice gradient du champ de vecteurs v'''
    dv1 = sv.gradient(v.dot(R.i))
    dv2 = sv.gradient(v.dot(R.j))
    dv  = sp.Matrix([[dv1.dot(R.i),dv1.dot(R.j)],[dv2.dot(R.i),dv2.dot(R.j)]])
    return dv

# calcul du gradient de V1 et V2
GradV1 = 0
GradV2 = 0
### BEGIN SOLUTION
GradV2=Gradient(V2)
GradV1=Gradient(V1)
display("Grad V1=",GradV1)
display("Grad V2=",GradV2)
### END SOLUTION

'Grad V1='

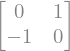
'Grad V2='

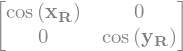
# calcul de la vorticité de V1 et V2
Omega1 = 0
Omega2 = 0
### BEGIN SOLUTION
Omega1 = sv.curl(V1)/2
Omega2 = sv.curl(V2)/2
display("Omega1=",Omega1)
display("Omega2=",Omega2)
### END SOLUTION

'Omega1='

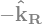
'Omega2='

# calcul de la matrice de déformation
D1 = 0
D2 = 0
### BEGIN SOLUTION
D1 = (GradV1+GradV1.transpose())/2
D2 = (GradV2+GradV2.transpose())/2
display("D1=",D1)
display("D2=",D2)
### END SOLUTION

'D1='

'D2='

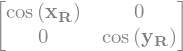
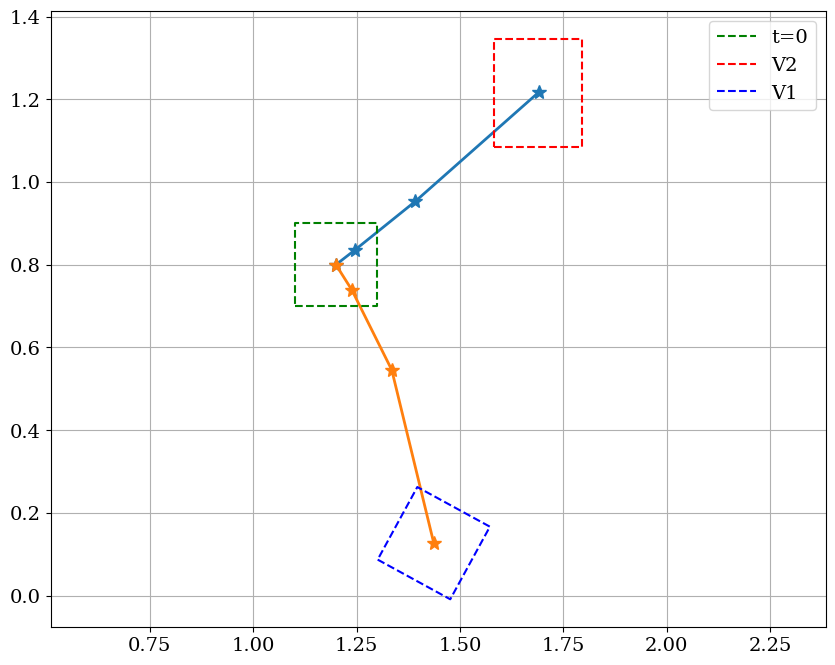
3.7. Trajectoires d’une particule

• Tracer les trajectoires des points A,B,C et D partant du meme point P avec les 2 champs

• Analyser le résultat

plt.figure(figsize=(10,8))
plt.plot(TP2[:,0],TP2[:,1],'-*',lw=2,ms=10)
plt.plot(TP1[:,0],TP1[:,1],'-*',lw=2,ms=10)

plt.plot([TA2[0,0],TB2[0,0],TC2[0,0],TD2[0,0],TA2[0,0]], 
         [TA2[0,1],TB2[0,1],TC2[0,1],TD2[0,1],TA2[0,1]],'--g',label='t=0')
plt.plot([TA2[-1,0],TB2[-1,0],TC2[-1,0],TD2[-1,0],TA2[-1,0]],
         [TA2[-1,1],TB2[-1,1],TC2[-1,1],TD2[-1,1],TA2[-1,1]],'--r',label='V2')
plt.plot([TA1[-1,0],TB1[-1,0],TC1[-1,0],TD1[-1,0],TA1[-1,0]],
         [TA1[-1,1],TB1[-1,1],TC1[-1,1],TD1[-1,1],TA1[-1,1]],'--b',label='V1')
plt.legend()
plt.grid('on')
plt.axis('equal');

3.8. FIN