Un pipeline graphique permet de calculer la couleur des pixels d'une image représentant une scène 3d éclairée par une ou plusieurs sources de lumières. Le pipeline openGL basé sur la rasterization / fragmentation est une solution particulière. On peut résumer son fonctionnement :
ou en gros
à la fin du parcours, tous les pixels contiennent la profondeur du triangle le plus proche de la camera ainsi que sa couleur.
le lancer de rayon fonctionne dans l'autre sens :
à première vue, les 2 solutions ne sont pas très différentes. Pourtant, il y a une différence fondamentale, le lancer de rayons fonctionne pour un ensemble de rayons quelconque. Dans l'exemple ci-dessus, les 2 images seront identiques. Mais on peut facilement créer de nouveaux rayons pour tester la visibilité des sources de lumière et ajouter très simplement les ombres dans l'image, ce qui est plus difficile à faire avec openGL, par exemple.
Une autre différence importante est ce que l'on peut calculer l'intersection d'un rayon avec d'autres objets que des triangles : des spheres, des cubes, des plans, des cylindres, des cones, des tores, des fractales, des champs de distances, des fonctions implicites, etc. sans avoir à trianguler la surface de ces objets. Par contre, il faudra écrire les différentes fonctions d'intersections.
rayon ?
Un rayon est une droite (ou un segment) dans l'espace (de la scène, par exemple) qui passe par le centre d'un pixel dans l'image. Mais il faut connaitre au moins 2 points pour représenter une droite. lesquels ? L'idée est que le rayon est l'ensemble des points de la scène qui se projettent sur le centre du pixel.
Quelles sont les coordonnées du centre d'un pixel dans le repère de la scène ? Il suffit de se rappeller que l'on peut transformer des coordonnées du repère image vers le repère de la scène en utilisant les transformations inverses des transformations standards. si on connait des coordonnées \( p_{scene} \) dans le repère de la scène, on peut écrire :
\[ q_{image} = Image \times Projection \times View \times p_{scene} \]
et
\[ p_{scene} = ( Image \times Projection \times View )^{-1} \times q_{image} \]
Quelles sont les coordonnées d'un pixel dans le repère \( Image \) ? On connait directement x et y, il ne reste plus que z ? Par définition, z = 0 sur le plan proche du frustum de la camera et z = 1 sur le plan far du frustum. repassez dans le cours d'intro sur les transformations si ce n'est pas clair.
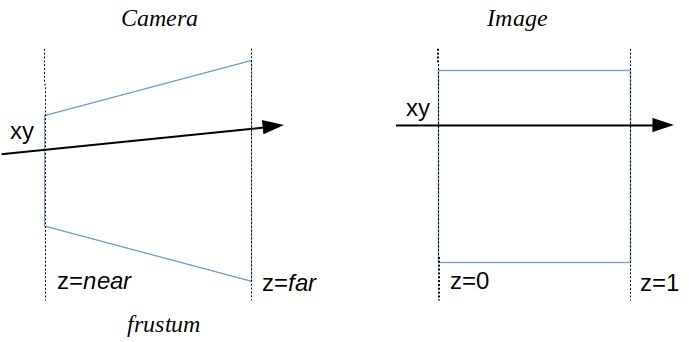
Résultat, on peut calculer les coordonnées de 2 points sur le rayon : x, y sur le plan near (z = 0), et x, y sur le plan far (z = 1) :
\[ origine_{scene} = ( Image \times Projection \times View )^{-1} \times \begin{bmatrix} x \\ y \\ 0 \end{bmatrix}\\ extremité_{scene} = ( Image \times Projection \times View )^{-1} \times \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}\\ \]
On peut donc représenter le rayon par les 2 points : origine et extremité. Mais en général, pour calculer les intersections avec les objets, on utilise plutot une autre convention : origine et direction. direction est le vecteur entre l'origine et l'extremité \( direction = extremité - origine \).
remarque : on connait un autre point sur le rayon, c'est le centre de projection de la camera, ou la position de la camera. Les coordonnées sont (0, 0, 0) dans le repère camera :
\[ origine_{scene} = ( View )^{-1} \times \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix}\\ \]
intersection ?
Il ne reste plus qu'à trouver comment calculer l'intersection d'un rayon / d'une droite avec les objets qui composent la scène.
Il faut exprimer le fait qu'une intersection représente un point du rayon et un point de l'objet. permière question, comment représenter un point sur le rayon ? la solution classique utilise la forme paramétrique des droites : \( p(t) = o + t \vec{d} \), \( t \) identifie un point sur la droite / le rayon. il represente la position du point sur la droite.
Lorsque le rayon est un segment, il "contient" tous les points entre son origine et son extremite : \( p(t)= o + t \vec{d} \) avec \( t \in [0 .. 1]\). on peut bien sur retrouver l'origine et l'extrémité du segment : \( p(0)= origine \) et \( p(1) = extremite \).
Il est également possible de représenter une demi-droite infinie au lieu d'un segment, dans ce cas \( t \in [0 .. \infty)\), et l'extremité n'existe pas, on ne connait que l'origine et la direction du rayon.
De manière générale pour décrire un rayon on utilise, \( o \), \( \vec{d} \) et la borne de l'intervalle \( t_{max} = 1 \) ou \( \infty \) selon le cas :
attention : Les calculs d'intersection qui sont décrits juste après se font avec la droite infinie qui porte le rayon. Lorsque le calcul trouve une ou plusieurs intersections, il faut vérifier qu'elles se trouvent dans l'intervalle \( [0 .. t_{max}] \) du rayon. La droite infinie peut toucher un objet, mais pas nécessairement le rayon.
plan
comment décrire l'ensemble de points sur un plan ? il existe de nombreuses manières, mais l'idée est de choisir une représentation qui permet d'écrire le calcul de l'intersection comme la recherche du zero d'une fonction.
On peut représenter un plan par un point \( a \) et une normale \( \vec{n} \), noté \( plan(a, \vec{n}) \) et déterminer l'ensemble des points \( p \) appartenant au plan comme les zeros de la forme implicite :
\[ \vec{n} \cdot \vec{ap} = 0 \]
remarque : les points \( p \) sont sur le plan si les vecteurs \( \vec{ap} \) et \( \vec{n} \) sont perpendiculaires, leur produit scalaire est nul dans ce cas.
calculer l'intersection du rayon et du plan se resume à trouver le point du rayon \( p(t) \) qui se trouve aussi sur le plan. le point d'intersection vérifie les 2 propriétés en même temps :
\[ \vec{n} \cdot \vec{a p(t)} = 0 \]
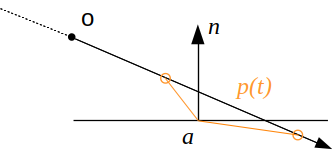
rappel : \( p(t) = o + t\vec{d} \) désigne un point du rayon.
il ne reste plus qu'à trouver quelle valeur de t vérifie ces conditions :
\[ \begin{eqnarray*} \vec{n} \cdot \vec{ap(t)} & = & 0\\ \vec{n} \cdot ((o + t \vec{d}) - a) & = & 0\\ \vec{n} \cdot ((o - a) + (t \vec{d})) & = & 0\\ \vec{n} \cdot (o - a) + \vec{n} \cdot (t \vec{d}) & = & 0\\ \vec{n} \cdot (o - a) + t (\vec{n} \cdot \vec{d}) & = & 0\\ t (\vec{n} \cdot \vec{d}) & = & - \vec{n} \cdot (o - a)\\ t & = & \frac{- \vec{n} \cdot (o - a)}{\vec{n} \cdot \vec{d}}\\ t & = & \frac{\vec{n} \cdot (a - o)}{\vec{n} \cdot \vec{d}}\\ \end{eqnarray*} \]
rappel : calcul avec des points, des vecteurs et des produits scalaires, cf wikipedia
on peut remarquer que, sans trop de surprise, un rayon intersecte toujours un plan, sauf lorsque le rayon est parallele au plan et que la direction du rayon et la normale du plan sont perpendiculaires.
Par contre, il ne faut pas oublier que l'on ne s'interresse qu'aux intersections se trouvant devant la camera, c'est à dire \( t > 0 \), il faut bien faire la différence entre les intersections de la droite et des objets testés et les intersections du rayon (la demi droite positive) avec les objets...
cube
On peut représenter un cube par les plans qui portent chaque face. pour chaque axe, il y a une paire de plans parallèles : le rayon entre dans le cube par un plan et ressort de l'autre coté, par l'autre plan. Le rayon traverse l'espace compris entre les 2 plans pour un intervalle \( t \in [t_{min} .. t_{max}] \).
remarque : si le rayon est orienté dans l'autre sens, s'il traverse l'espace de la droite vers la gauche, il faut inverser les bornes de l'intervalle \( [t_{min} .. t_{max}] \). Les bornes de l'intervalle doivent vérifier \( t_{min} \leq t_{max} \)
On peut décrire un cube par un centre \( c \) , et 3 axes \( \vec{i}, \vec{j}, \vec{k} \). Les calculs d'intersections rayon / plans sont réalisés comme ci-dessus :
- \( plan( c + \vec{i}, \vec{i} ) \), \( plan(c - \vec{i}, - \vec{i}) \)
- \( plan( c + \vec{j}, \vec{j} ) \), \( plan(c - \vec{j}, - \vec{j}) \)
- \( plan( c + \vec{k}, \vec{k} ) \), \( plan(c - \vec{k}, - \vec{k}) \)
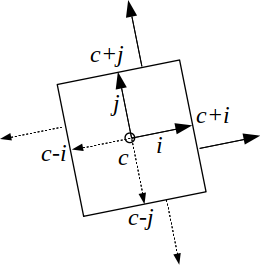
Pour calculer l'intersection avec le cube, il faut calculer ces 3 intervalles (un par paire de plans / par axe) et vérifier que les intervalles se chevauchent : que leur intersection n'est pas vide.
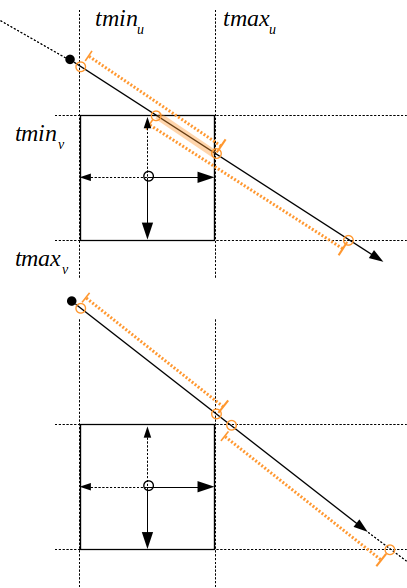
Il y a aura une intersection si \( [t_{min_i} .. t_{max_i}] \cap [t_{min_j} .. t_{max_j}] \cap [t_{min_k} .. t_{max_k}] \cap [0 .. t_{max}] \neq \phi \)
cube aligné sur les axes
c'est la meme chose, mais les axes sont implicitement \( \vec{x}, \vec{y}, \vec{z} \). Les produits scalaires d'un vecteur \( \vec{v} \) avec les axes d'un repère se simplifient :
\[ \vec{x} \cdot \vec{v} = \begin{bmatrix} 1\\ 0\\ 0 \end{bmatrix} \cdot \begin{bmatrix} v_x\\ v_y\\ v_z \end{bmatrix} = v_x, \, \vec{y} \cdot \vec{v} = \begin{bmatrix} 0\\ 1\\ 0 \end{bmatrix} \cdot \begin{bmatrix} v_x\\ v_y\\ v_z \end{bmatrix} = v_y, \mbox{ et } \vec{z} \cdot \vec{v} = \begin{bmatrix} 0\\ 0\\ 1 \end{bmatrix} \cdot \begin{bmatrix} v_x\\ v_y\\ v_z \end{bmatrix} = v_z \]
au final, ce n'est pas si compliqué :
il y a encore quelques astuces de calculs pour éviter les problèmes lorsque la direction du rayon est parallèle à un axe : par exemple pourquoi le code précédent multiplie par l'inverse d'une valeur au lieu de calculer directement la division...
sphere
Pour une sphère de centre \( c \), et de rayon \( r \), même stratégie : les points de l'espace sont sur la sphère s'ils se trouvent à la bonne distance du centre :
\[ \begin{eqnarray*} | p - c | & = & r \\ | p - c | - r & = & 0 \\ | p - c |^2 - r^2 & = & 0\\ (p - c) \cdot (p - c) - r^2 & = & 0 \end{eqnarray*} \]
rappel : on a utilisé une relation entre le produit scalaire et (le carré de) la longueur du vecteur : \( \vec{u} \cdot \vec{u} = |u|^2 \)
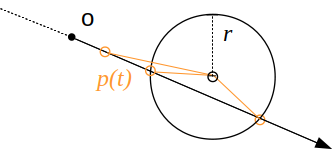
il ne reste plus qu'à trouver la valeur de \( t \) pour que \( p(t) \), le point sur le rayon soit aussi sur la sphère :
\[ \begin{eqnarray*} (p(t) - c) \cdot (p(t) - c) - r^2 & = & 0\\ (o + t\vec{d} - c) \cdot (o + t\vec{d} - c) - r^2 & = & 0\\ ((o - c) + t\vec{d}) \cdot ((o - c) + t\vec{d}) - r^2 & = & 0\\ (\vec{d} \cdot \vec{d}) t^2 + 2\vec{d} \cdot (o - c) t + (o - c) \cdot (o - c) - r^2 & = & 0\\ \end{eqnarray*} \]
il faut relire attentivement ce résultat, mais il est sous une forme assez simple au final :
\[ \begin{eqnarray*} a t^2 + b t + k & = & 0\\ a & = & \vec{d} \cdot \vec{d}\\ b & = & 2\vec{d} \cdot (o - c)\\ k & = & (o - c) \cdot (o - c) - r^2 \end{eqnarray*} \]
il ne reste plus qu'à calculer les zeros du polynome : les détails sont sur wikipedia et ici et ce résultat est assez intuitif : une droite peut passer à coté de la sphère, la toucher en un seul point, ou la traverser en 2 points.
si \( b^2 - 4ak > 0 \), les solutions s'écrivent :
\[ \begin{eqnarray*} t_1 & = & \frac{-b + \sqrt{b^2 - 4ak}}{2a}\\ t_2 & = & \frac{-b - \sqrt{b^2 - 4ak}}{2a}\\ \end{eqnarray*} \]
Par contre, il ne faut pas oublier que l'on ne veut que les intersections avec le rayon, pas les intersections avec la droite. il faut donc aussi vérifier le signe des solutions \( t_1 > 0 \) et \( t_2 > 0 \)
pour les curieux : on peut gagner pas mal de temps en ne calculant qu'une seule solution, et en normalisant \( \vec{d} \) à l'avance, \( | \vec{d} |= 1 \) et aussi \(| \vec{d} |^2 = \vec{d} \cdot \vec{d} = a = 1\). Selon le cas, on sait à l'avance que l'origine du rayon se trouve à l'exterieur de la sphère, et il suffit de calculer la plus petite racine \( > 0 \).
triangle
Il y a plusieurs manières de faire ce calcul. par exemple, calculer l'intersection du rayon et du plan qui porte le triangle (représenté par un sommet du triangle et sa normale géométrique, \( a \) et \( \vec{n}= \vec{ab} \times \vec{ac} \), puis vérifier que le point du plan est aussi à l'intérieur du triangle, comme expliqué pour le cours d'introduction en L3.
Il faut aussi se rappeler que l'on veut les coordonnées barycentriques du point d'intersection pour obtenir les mêmes informations que la rasterization / fragmentation, pour interpoler les attributs des sommets du triangle, ie les normales et les coordonnées de texture, par exemple.
on peut représenter un point dans le plan du triangle \( abc \) à l'aide des coordonnées barycentriques :
\[ p(\alpha, \beta, \gamma) = \alpha a + \beta b + \gamma c \]
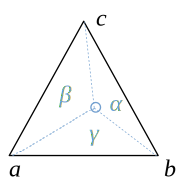
rappel : les coordonnées barycentriques sont tout simplement les aires normalisées des 3 triangles formés avec le point et chaque arête.
les points à l'intérieur du triangle vérifient quelques propriétés supplémentaires :
\[ \begin{eqnarray*} \alpha & \geq & 0 \mbox{ et }\alpha \leq 1\\ \beta & \geq & 0 \mbox{ et }\beta \leq 1\\ \gamma & \geq & 0 \mbox{ et }\gamma \leq 1\\ \alpha + \beta + \gamma & =& 1 \end{eqnarray*} \]
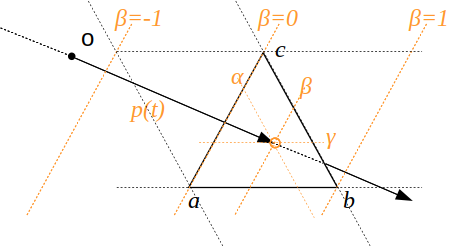
remarque : tous les points du plan ont des coordonnées barycentriques par rapport au triangle \( abc \), par contre elles sont \( < 0 \) ou \( > 1 \).
\( \alpha \) peut être recalculée en fonction des 2 autres : \( \alpha= 1 - \beta - \gamma \) et on utilise la forme simplifiée :
\[ p(\beta, \gamma) = (1 - \beta - \gamma) a + \beta b + \gamma c \]
remarque : il existe plusieurs conventions pour cette simplification, n'importe laquelle des 3 peut etre calculée implicitement.
il ne reste plus qu'à écrire qu'un point doit être en même temps sur le rayon et dans le triangle :
\[ \begin{eqnarray*} p(t) & = & p(\beta, \gamma)\\ o + t\vec{d} & = & (1 - \beta - \gamma) a + \beta b + \gamma c\\ o + t\vec{d} & = & a + \beta (b - a) + \gamma (c - a)\\ - t\vec{d} + \beta (b - a) + \gamma (c - a) & = & (o - a) \\ \end{eqnarray*} \]
on obtient un système linéaire, 3 équations et 3 inconnues ( \( t, \beta, \gamma \)), une solution élégante n'utilisant que des produits scalaires et vectoriels est proposée dans cet article :
une autre explication plus géométrique est résumée sur la page du cours d'initiation des L3. les 384 manières de calculer le volume signée d'un tetraedre et comment utiliser cette propriété pour calculer l'intersection entre un rayon et un triangle sont résumées dans :
remarque : c'est la même idée qu'en 2d pour déterminer qu'un point se trouve à l'intérieur du triangle. si le point est du bon coté de chaque arête, le point est à l'intérieur du triangle. en 3d, on va vérifier que le rayon se trouve du bon coté des plans formés par l'origine du rayon et chaque arête. en 2d on calcule l'aire signée d'un triangle, en 3d, on utilise le volume signé d'un tetraedre...
en pratique
Comment calculer une image avec du lancer de rayons et des triangles ? (et une camera) (et une source de lumiere) (et des matieres...)
et voila, pas bien compliqué !! malgré des explications un peu longues...
remarque : la boucle qui calcule les intersections fonctionne de la meme maniere quelque soit le type des objets :
dans le code d'exemple, la fonction Triangle::intersect() ne renvoie vrai que si une intersection valide (dans l'intervalle [0 .. hit.t]) existe, ce qui simplifie pas mal l'ecriture de la boucle...
bon, afficher des pixels rouges, ne permet pas vraiment de vérifier que les intersections fonctionnent correctement. on peut construire une couleur avec le résultat de l'intersection :
le sommet \( a \) des triangles apparait en rouge, le sommet \( b \) en vert et le sommet \( c \) en bleu...

matière diffuse, source de lumière, et lumière réfléchie...
pour calculer la couleur des pixels en fonction de la matière du triangle et de sa normale interpolée, il faut ajouter quelques éléments :
- interpoler les normales des sommets du triangle en fonction des coordonnées de l'intersection,
- récupérer la couleur diffuse de la matiere du triangle,
- récupérer la position de la source de lumière,
- calculer la lumière réfléchie vers la camera / l'origine du rayon.
pour interpoler la normale au point d'intersection en fonction des normales des sommets du triangle, il suffit de ré-utiliser les coordonnées barycentriques du point d'intersection avec le triangle, exactement comme le pipeline openGL :
\[ \vec{n}(\beta, \gamma) = (1 - \beta - \gamma) \vec{n_a} + \beta \vec{n_b} + \gamma \vec{n_c} \]
pour récupérer la couleur de la matière :
pour trouver les sources de lumière, il faut parcourir les triangles du Mesh et vérifier que leur matière émet de la lumière. Comme c'est un peu long, ce sera fait une seule fois au début du programme :
Il ne reste plus qu'à calculer la lumière réfléchie par une matière diffuse, comme dans le tp précédent (cf lumière et matière et shader et brdf)
et voila :
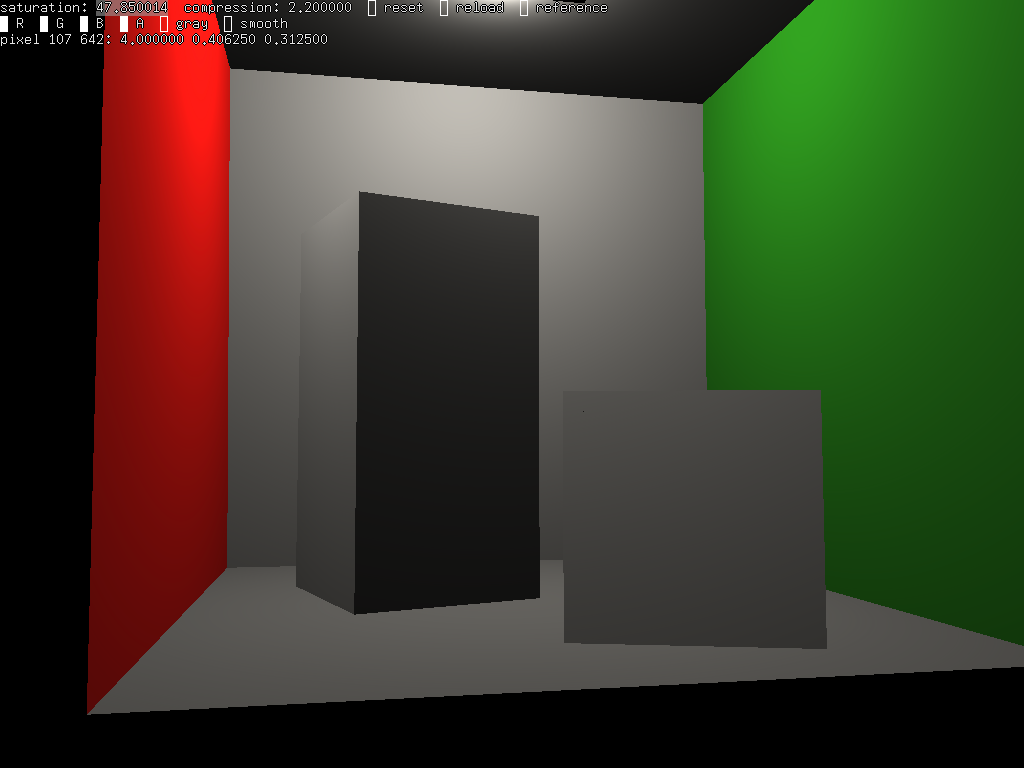
il ne reste plus qu'à ajouter les ombres...
indication : il suffit de construire un rayon entre p et s, le point sur la source, et de vérifier qu'il n'y a pas d'intersection entre eux, pour que la lumière arrive au point p, sinon p est à l'ombre...
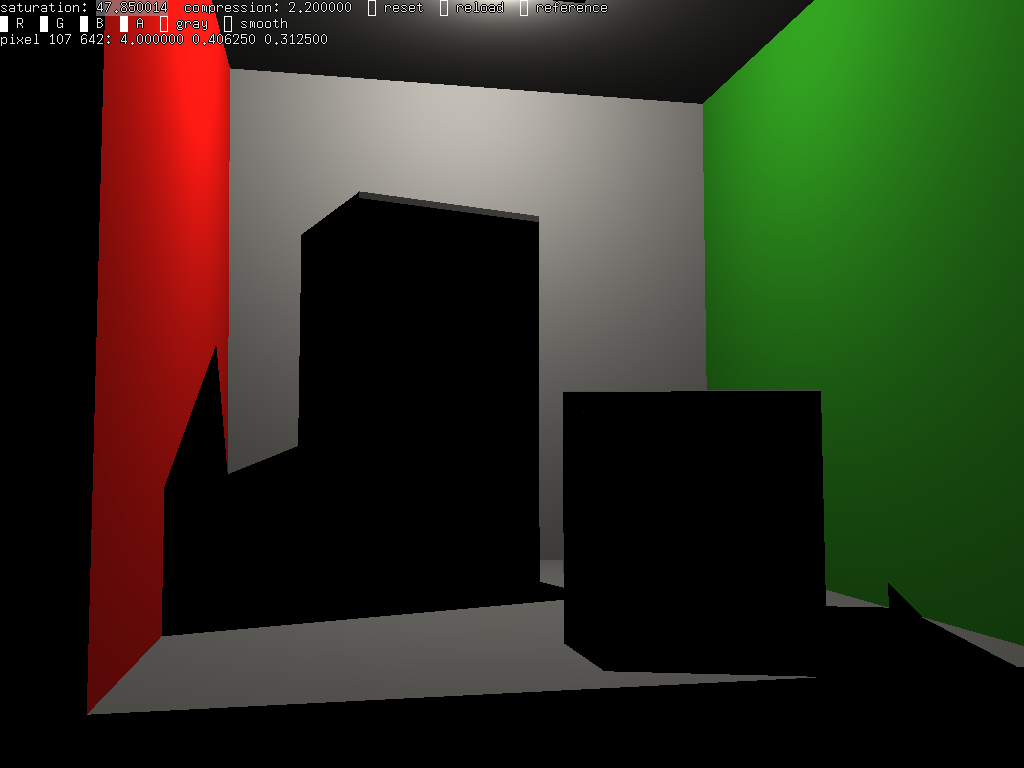
et alors ?
Et avec d'autres objets, qu'est ce qui change ? Il faut écrire les fonctions d'intersection rayon / objet pour chaque cas.
openGL dessine les triangles "tout seul", par contre manipuler l'api d'openGL est probablement plus compliqué. mais on profite des processeurs parallèles de la carte graphique qui sont particulièrement rapides.
pour les curieux : oui, bien sur, on peut écrire un shader openGL qui calcule les intersections rayons / triangles de la même manière, cf tuto_raytrace_fragment.cpp et raytrace.glsl
la version en ligne de PBRT (un livre de référence sur le lancer rayons et les calculs réalistes) propose également les tests d'intersections pour plusieurs objets :
- cube aligné sur les axes,
- sphère,
- cylindres,
- disques,
- cones et paraboloides,
- triangles,
- courbes épaisses, courbes de Bézier extrudées pour décrire des cheveux, de la fourrure, de l'herbe...
Les fonctions implicites permettent aussi de faire énormement de choses, regardez quelque exemples sur shadertoy.com, presque tous les shaders utilisent une variante du lancer de rayon, le lancer de sphère / sphere tracing. En attendant le cours de M2 d'Eric Galin sur le sujet, vous pouvez jeter un ou plusieurs yeux sur le blog d'Inigo Quilez, le créateur de shadertoy.
Mais le principal problème du lancer de rayon est sa lenteur, du coup il est nécessaire de réfléchir un peu pour calculer des intersections sur plus de 100 objets. cf le lancer de rayons, ça rame ? ou pas ?.
annexe
il manque les définitions des structures Hit et Triangle :
le code complet est dans tuto_rayons.cpp