le lancer de rayons, ça rame ? ou pas ?

Pour l'instant le lancer de rayon se résume à une double boucle, pas très efficace lorsqu'il y a beaucoup de rayons et beaucoup d'objets :

objets[]
rayons[]
hit[]
 
pour chaque rayon
    hit[rayon].t= max
    pour chaque objet
        (t, uv) = intersection rayon / objet
        si t < hit[rayon].t
            hit[rayon]= (t, uv)

que peut-on faire pour éviter de calculer la totalité des intersections et réduire la complexité de cette fonction ?

L'idée est assez simple : si un rayon passe loin d'un objet ou d'un groupe d'objets, ce n'est pas la peine de calculer toutes ces intersections... Comment réaliser ce test rapide sur tout le groupe d'objet ? il suffit de choisir une forme simple avec une fonction d'intersection rapide et de l'utiliser pour représenter la région de l'espace occuppée par le groupe d'objet :

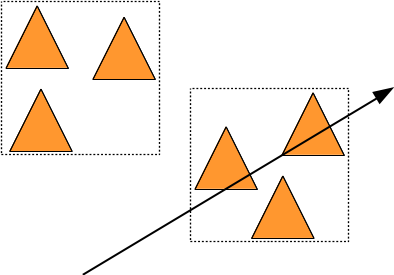
On dit que cette forme simple et rapide à tester est l'englobant du groupe d'objet. Si un rayon ne touche pas l'englobant du groupe, il n'est pas nécessaire de calculer les intersections du rayon avec tous les objets du groupe. Dans cet exemple, on a testé 2 boites et 3 triangles, au lieu de 6 triangles. ce ne sera plus rapide que si tester 2 boites est plus rapide que tester 3 triangles...

Mais bien sur, il faut maintenant construire cet englobant à partir des objets, ou d'une partie des objets. et selon la complexité de chaque étape, l'algorithme complet pourra être plus interessant que la double boucle, ou pas...

Voila l'idée générale, qui repartit les triangles en 2 groupes / englobants si c'est interessant, ou qui utilise la double boucle directe.

// version directe
direct( rayons, objets ) :
    pour chaque rayon
        pour chaque objet
            intersection, etc.
 
// version "efficace"
repartition( englobant, rayons, objets ) :
    si pas de rayons ou pas d''objets
        arreter
    si rayons < limite ou objets < limite
        direct(rayons, objets)
    sinon
        // decouper le probleme
        découper l''englobant en 2 regions ("petits" englobants)
        pour chaque region
            { r } = rayons qui touchent la region
            { t } = objets à l''interieur de la region
            repartition(region, { r }, { t })

le paramètre limite aura une grosse influence sur l'algorithme, en fonction du temps necessaire pour couper un englobant en 2, repartir les objets dans les 2 englobants et tester quels rayons touchent chaque englobant.

on peut illustrer les différentes étapes de l'algorithme, en utilisant un cube aligné sur les axes comme englobant :

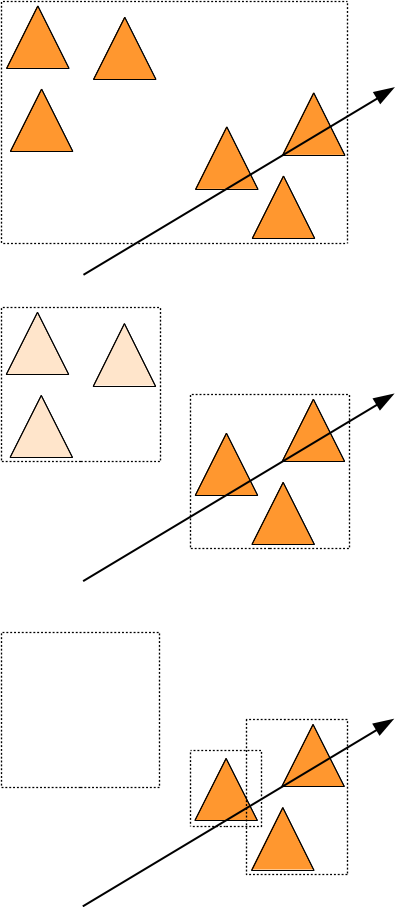
Répartition

Il y a encore quelques détails à régler avant d'écrire la solution complète : si on découpe un englobant en 2 parties, il peut très bien arriver qu'un triangle touche les 2 parties, il faudra donc inclure le triangle dans les 2 ensembles de triangles testés par la suite de l'algorithme. ce qui veut dire allouer de la mémoire à chaque appel récursif pour représenter l'ensemble { t }... et ça va être très long.

On peut faire le contraire : choisir pour chaque triangle dans quel englobant le mettre et calculer ensuite la taille des englobants (en fonction des triangles qui leur sont associés). De cette manière chaque triangle n'apparait que dans un seul ensemble { t } et il n'est plus nécessaire de réallouer de la mémoire. On peut même faire mieux : on peut décider que les triangles du premier ensemble seront au début du tableau de triangles et que les autres sont placés après. si tous les triangles sont dans un tableau T, après la répartition, on peut repérer chaque ensemble de triangles { t } par un indice de début et un indice de fin.

// au debut
Triangle T[]= { A, B, C, D, E, F, G, H };
 
// on decide de repartir les triangles comme ca :
// T1= { A, C, F, G };
// et
// T2= { B, D, E, H };
 
// apres la répartition, on peut ranger les triangles dans T[]
T[]= { A, C, F, G , B, D, E, H };
// et representer T1 avec :
int debut1 = 0;
int fin1= 4;
// les 4 premiers triangles
// et T2
int debut2= 4;
int fin2= 8;
// les 4 suivants

tout ça pour dire que le tableau de triangles va se trier au fur et à mesure des appels récursifs de repartition( ) et qu'il suffit de passer les indices debut/fin de chaque partie en paramètre.

En pratique, une solution de répartition qui fonctionne bien utilise une boite alignée sur les axes comme englobant. Pour découper l'englobant en 2 régions, il suffit de trouver quel axe de l'englobant est le plus long, et de le couper en 2, au milieu. Ensuite, il suffit de tester un point de chaque triangle pour décider de l'associer à la region 1 ou 2, selon sa position par rapport au plan qui coupe l'englobant par le milieu.

Quel point choisir pour répartir un triangle dans l'ensemble T1 ou T2 ? Si l'on regarde le fonctionnement de l'algorithme, les objets sont répartis en utilisant leur boite englobante. Et le centre de la boite englobante est probablement la meilleure solution.

Dernier détail pratique, comment écrire la répartition des triangles ?

// au debut :
// Triangle T[]= { A, B, C, D, E, F, G, H };
 
        découper l''englobant en 2 regions ("petits" englobants)
        pour chaque region
            { t } = objets à l''interieur de la region
 
// apres la repartition :
// T[]= { A, C, F, G , B, D, E, H };
// T1_debut= 0; T1_fin= 4;
// T2_debut= 4; T2_fin= 8;

en fait, c'est un algorithme classique disponible dans la librairie standard c++ : std::partition() l'idée est de tester chaque élément d'un tableau et de décider s'il doit etre placé au début ou à la fin du tableau, en fonction du résultat du test. Tous les éléments pour lesquels le test est vrai sont placés au début du tableau, et ceux pour lesquels le test est faux sont placés à la suite, à la fin du tableau. Et la fonction std::partition() renvoie l'indice du premier élément de la 2ieme partie du tableau. Il ne reste plus qu'à écrire le test. On utilise une structure qui définit operator() ( ... ) const, qui renvoie un bool. cette fonction de test des éléments s'appelle un prédicat :

// exemple: partitionner les elements de T, les valeurs multiple de m seront au debut du tableau, les autres à la fin du tableau
#include <algorithm>
 
// predicat 
struct test
{
    int m;
    test( const int _m ) : m(_m) {}
    
    bool operator() ( const int &x ) const { return (x%m) == 0; }       // renvoie vrai si x est multiple de m
};
 
std::vector<int> tab= { 1, 2, 3, 4, 6, 8, 9, 11, 13, 14, 15, 16 };
 
// partitionne les elements du tableau, multiples de 3 au debut, les autres à la suite
int *p= std::partition(tab.data(), tab.data() + tab.size(), test(3));
// partition renvoie un pointeur sur l'élément, retrouver son indice...
int pivot= std::distance(tab.data(), p);
 
// partie 1 au debut du tableau : de l'indice 0 à pivot
for(int i= 0; i < pivot; i++)
    printf("%d ", tab[i]);
// 15 9 3 6 
 
// partie 2 à la fin du tableau : de pivot à la fin
for(int i= pivot; i < int(tab.size()); i++)
    printf("%d ", tab[i]);
// 4 8 2 11 13 14 1 16

Les ensembles de triangles et des rayons sont répresentés par des tableaux et les indices de début et fin. L'intersection directe de tous les rayons avec tous les triangles peut s'ecrire facilement :

void direct( 
    const std::vector<Triangle>& triangles, const int tbegin, const int tend,
    std::vector<RayHit>& rays, const int rbegin, const int rend )
{
    for(int i= rbegin; i < rend; i++)
    for(int k= tbegin; k < tend; k++)
        triangles[k].intersect(rays[i]);
}

On a maintenant tous les éléments pour écrire l'algorithme de répartition. Pour manipuler facilement les englobants, on peut utiliser :

struct BBox
{
    Point pmin, pmax;   // points extremes de l'englobant
    
    BBox( const Point& p ) : pmin(p), pmax(p) {}
    BBox( const Point& a, const Point& b ) : pmin(a), pmax(b) {}
    BBox( const BBox& b ) : pmin(b.pmin), pmax(b.pmax) {}
    
    // ajouter un point dans l'englobant
    BBox& insert( const Point& p ) { pmin= min(pmin, p); pmax= max(pmax, p); return *this; }
    BBox& insert( const BBox& b ) { pmin= min(pmin, b.pmin); pmax= max(pmax, b.pmax); return *this; }
    
    // position du centre de l'englobant sur un axe
    float centroid( const int axis ) const { return (pmin(axis) + pmax(axis)) / 2; }
};
 
BBox EmptyBox( ) { return BBox(Point(FLT_MAX, FLT_MAX, FLT_MAX), Point(-FLT_MAX, -FLT_MAX, -FLT_MAX)); }

Et voila l'algo principal :

void divide( const BBox& bounds, 
    std::vector<Triangle>& triangles, const int tbegin, const int tend,
    std::vector<RayHit>& rays, const int rbegin, const int rend )
{
    if(tbegin == tend || rbegin == rend)
        // plus de triangles ou de rayons, rien a faire...
        return;
        
    if(tend - tbegin <= 4)
    {
        // il ne reste plus que quelques triangles, finir les calculs d'intersection...
        direct(triangles, tbegin, tend, rays, rbegin, rend);
        return;
    }
    
    // axe le plus etire de l'englobant
    Vector d= Vector(bounds.pmin, bounds.pmax);
    int axis;
    if(d.x > d.y && d.x > d.z)  // x plus grand que y et z ?
        axis= 0;
    else if(d.y > d.z)          // y plus grand que z ? (et que x implicitement)
        axis= 1;
    else                        // x et y ne sont pas les plus grands...
        axis= 2;
 
    // coupe l'englobant au milieu
    float cut= bounds.centroid(axis);
    
    // repartit les triangles 
    Triangle *pm= std::partition(triangles.data() + tbegin, triangles.data() + tend, triangle_less1(axis, cut));
    int m= std::distance(triangles.data(), pm);
    
    // la repartition des triangles peut echouer, et tous les triangles sont dans la meme partie... 
    // forcer quand meme un decoupage en 2 ensembles de meme taille
    if(m == tbegin || m == tend)
        m= (tbegin + tend) / 2;
    
    // construit les englobants des triangles de la partie 1 / a gauche
    // les triangles se trouvent dans [tbegin .. m)
    BBox left= triangle_bounds(tbegin, m);
    
    // place les rayons qui touchent l'englobant au debut du tableau
    RayHit *prleft= std::partition(rays.data() + rbegin, rays.data() + rend, ray_less1(left));
    int rleft= std::distance(rays.data(), prleft);
    // les rayons qui touchent l'englobant se trouvent dans [rbegin .. rleft)
    
    // recursion sur T1 et les rayons qui touchent l'englobant de T1
    divide(left, triangles, tbegin, m, rays, rbegin, rleft);
    
    // on recommence pour la partie 2 / a droite
    // les triangles se trouvent dans [m .. tend)
    BBox right= triangle_bounds(m, tend);
    
    // place les rayons qui touchent l'englobant au debut du tableau
    RayHit *prright= std::partition(rays.data() + rbegin, rays.data() + rend, ray_less1(right));
    int rright= std::distance(rays.data(), prright);
    // les rayons qui touchent l'englobant se trouvent dans [rbegin .. rright)
    
    // recursion sur T2 et les rayons qui touchent l'englobant de T2
    divide(right, triangles, m, tend, rays, rbegin, rright);
}
 
BBox triangle_bounds( const int begin, const int end )
{
    BBox bounds= EmptyBox();
    for(int i= begin; i < end;i++)
        bounds.insert(triangles[i].bounds());
    
    return bounds;
}

il manque les prédicats qui testent les rayons et les triangles :

struct ray_less1
{
    BBox bounds;
    
    ray_less1( const BBox& _bounds ) : bounds(_bounds) {}
    
    bool operator() ( const RayHit& ray ) const
    {
        // renvoie vrai si le rayon touche l'englobant
        return bounds.intersect(ray);
    }
};

et

struct triangle_less1
{
    int axis;
    float cut;
    
    triangle_less1( const int _axis, const float _cut ) : axis(_axis), cut(_cut) {}
    
    bool operator() ( const Triangle& triangle ) const
    {
        // re-construit l'englobant du triangle
        BBox bounds= triangle.bounds();
        // renvoie vrai si le triangle est dans la partie gauche / avant le plan qui coupe l'englobant au milieu
        return bounds.centroid(axis) < cut;
    }
};

remarque : oui, bien sur on peut aussi utiliser des lambdas c++ pour écrire les prédicats, c'est la même chose. par exemple :

// avec un predicat
// Triangle *pm= std::partition(triangles.data() + tbegin, triangles.data() + tend, triangle_less1(axis, cut));
// int m= std::distance(triangles.data(), pm);
 
// idem mais avec une lambda 
Triangle *pm= std::partition(triangles.data() + tbegin, triangles.data() + tend, 
    [axis, cut] ( const Triangle& triangle ) 
    {
        // re-construit l'englobant du triangle
        BBox bounds= triangle.bounds();
        // renvoie vrai si le triangle est dans la partie gauche / avant le plan qui coupe l'englobant au milieu
        return bounds.centroid(axis) < cut;
    }
);
int m= std::distance(triangles.data(), pm);

et alors ?

est-ce que tout ca est interessant ?? pour la cornell box, qui ne comporte que 32 triangles, c'est un peu mieux :

• direct() 90ms
• divide() 80ms

et pour un objet plus gros, par exemple data/bigguy.obj, 3000 triangles :

• direct() 12400ms
• divide() 170ms

ca commence à etre mieux... petite remarque sur la complexite de l'algorithme de répartition, il y a presque 10 fois plus de triangles dans bigguy, mais le temps d'intersection n'est que ~2 fois plus important... pas mal.

code complet dans tuto_englobant.cpp

Par contre, il y a un petit inconvénient pour utiliser cet algorithme pour calculer une image, il faut construire le tableau de rayons pour l'utiliser et il serait plus simple et plus pratique de pouvoir tester rapidement un seul rayon à la fois. Un autre problème est lié au fait que les triangles sont re-triés à chaque fois : pour tous les rayons partant de la camera, puis les ombres (visibilité des sources de lumières), pour les reflets, etc... Dernier point embétant, il n'est pas facile de le paralléliser...

pour les curieux : cette méthode est décrite plus en détail :

• "Naive-Ray-Tracing: A divide-and-conquer approach", B. Mora, 11
• "Efficient Divide-And-Conquer Ray Tracing using Ray Sampling", K. Nabata, K. Iwasaki, Y. Dobashi, T. Nishita, 2013

BVH : arbre d'englobants

Le principal inconvénient de la solution précedente est que l'on re-trie plusieurs fois les triangles, pour chaque ensemble de rayons nécessaire au calcul de l'image (et construire l'ensemble de rayons à tester n'est pas toujours simple).

construction

Mais il n'est pas très compliqué de stocker les englobants construits par l'algorithme de répartition dans un arbre. Puis de parcourir cet arbre pour chaque rayon... Voici les englobants construits par l'algorithme de répartition, ainsi que les noeuds et l'arbre associé :

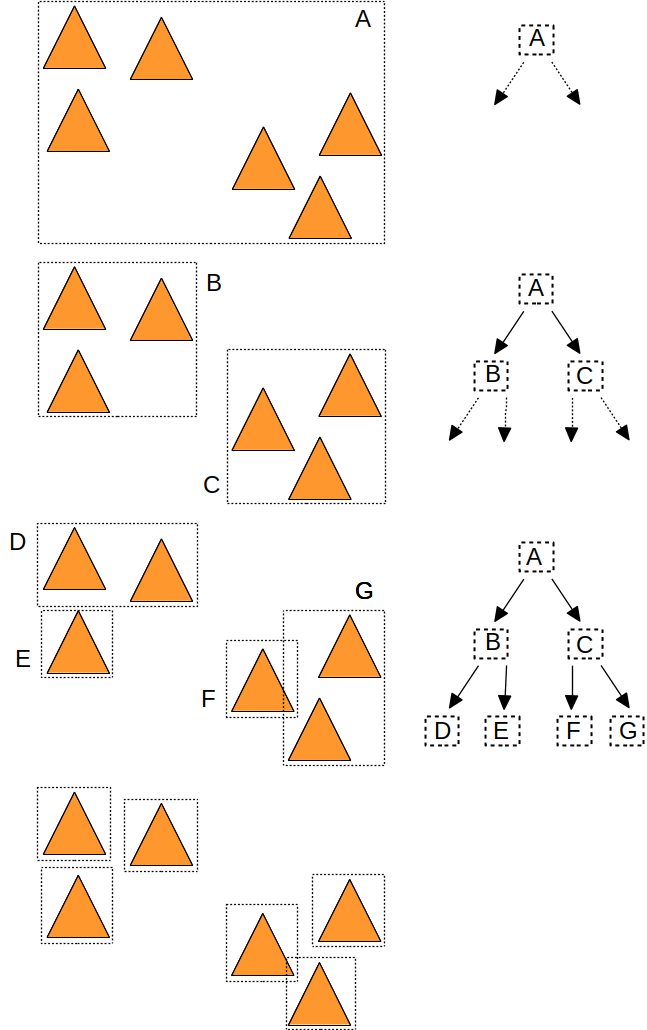
il suffit de modifier l'algorithme de répartition de la section précédente :

// rappel
repartition( englobant, rayons, objets ) :
    si rayons < limite ou objets < limite
        direct(rayons, objets)
    sinon
        // decouper le probleme
        découper l''englobant en 2 regions ("petits" englobants)
        pour chaque region
            { r } = rayons qui touchent la region
            { t } = objets à l''interieur de la region
            repartition(region, { r }, { t })

l'appel à la fonction direct() correspond à la création d'une feuille, et les appels à repartition() correspondent à la création des fils des noeuds internes. On n'a plus besoin des rayons, on veut simplement construire tous les groupes d'objets et leurs englobants :

construction( englobant, objets ) :
    si objets < limite
        renvoyer une feuille { englobant, objets }
    sinon
        // decouper le probleme
        découper l''englobant en 2 regions ("petits" englobants)
        { gauche, objets_gauche } = englobant et objets de la region 1
        { droite, objets_droite } = englobant et objets de la region 2
        fils gauche= construction(gauche, objets_gauche)
        fils droit= construction(droite, objets_droite)
        renvoyer un noeud interne { englobant, fils gauche, fils droit }

et l'algorithme renvoie le noeud racine de l'arbre. Ce type d'arbre s'appelle un BVH, pour Bounding Volume Hierarchy.

Ces deux algorithmes suivent le meme principe et à la fin les objets sont triés dans l'ordre des feuilles qui les référencent.

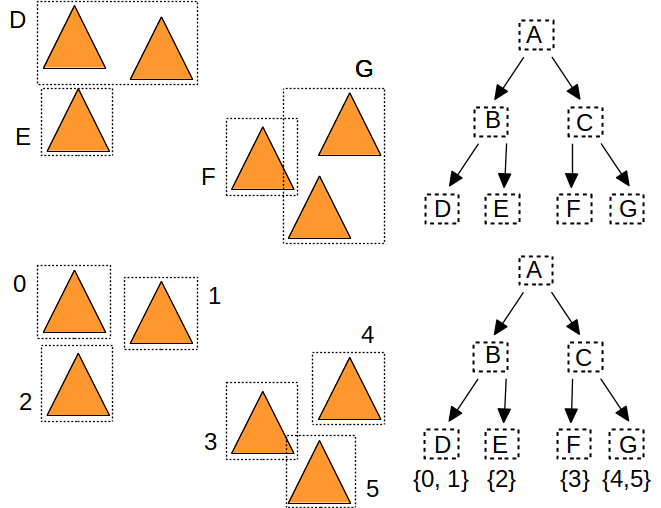
Bien sur, il reste quelques détails à régler : comment représenter les noeuds, les feuilles, les objets, etc. Le plus simple est d'utiliser la meme structure pour représenter les noeuds internes et les feuilles de l'arbre. Une autre simplification consiste à utiliser un tableau de noeuds, et à utiliser des indices pour désigner le fils gauche et le fils droit. Avec cette convention, on obtient cette représentation de noeud :

• noeud : un englobant, l'indice de son fils gauche, l'indice de son fils droit,
• feuille : un englobant, l'indice du premier objet dans le tableau trié des objets, et l'indice du dernier objet, ce sont les memes parametres que l'appel à direct() dans l'algorithme de répartition.

L'arbre est représenté par un tableau de noeud / feuille et le tableau des objets triés par la construction, ainsi que l'indice de la racine :

struct Node
{
    BBox bounds;
    int left;
    int right;
};
 
struct BVH
{
    std::vector<Node> nodes;
    std::vector<Triangle> triangles;
    
    int root;
};

on aurait également pu utiliser des entiers supplémentaires dans les feuilles (premier et dernier par exemple) pour stocker l'indice du premier et du dernier objet, mais il suffit de pouvoir faire la différence entre un noeud (interne) et une feuille. Du coup, on peut utiliser des valeurs négatives pour stocker les indices des objets et des valeurs positives pour stocker les indices des fils. Pour rendre le reste du code plus lisible, il suffit de cacher ces détails dans la structure Node :

struct Node
{
    BBox bounds;
    int left;
    int right;
    
    bool internal( ) const { return right > 0; }                        // renvoie vrai si le noeud est un noeud interne
    int internal_left( ) const { assert(internal()); return left; }     // renvoie le fils gauche du noeud interne 
    int internal_right( ) const { assert(internal()); return right; }   // renvoie le fils droit
    
    bool leaf( ) const { return right < 0; }                            // renvoie vrai si le noeud est une feuille
    int leaf_begin( ) const { assert(leaf()); return -left; }           // renvoie le premier objet de la feuille
    int leaf_end( ) const { assert(leaf()); return -right; }            // renvoie le dernier objet
};
 
// creation d'un noeud interne
Node make_node( const BBox& bounds, const int left, const int right )
{
    Node node { bounds, left, right };
    assert(node.internal());    // verifie que c'est bien un noeud...
    return node;
}
 
// creation d'une feuille
Node make_leaf( const BBox& bounds, const int begin, const int end )
{
    Node node { bounds, -begin, -end };
    assert(node.leaf());        // verifie que c'est bien une feuille...
    return node;
}

La construction de l'arbre est sans surprise, elle utilise la meme fonction de répartition std::partition(), et renvoie l'indice du noeud ou de la feuille crée :

struct BVH
{
    ...
    
    // construit un bvh pour l'ensemble de triangles
    int build( const std::vector<Triangle>& _triangles, const BBox& _bounds )
    {
        triangles= _triangles;  // copie les triangles pour les trier
        nodes.clear();          // efface les noeuds
        
        // construit l'arbre... 
        root= build(_bounds, 0, triangles.size());
        // et renvoie la racine
        return root;
    }
    
protected:
    // construction d'un noeud
    int build( const BBox& bounds, const int begin, const int end )
    {
        if(end - begin <= 2)
        {
            // inserer une feuille et renvoyer son indice
            int index= nodes.size();
            nodes.push_back( make_leaf(bounds, begin, end) );
            return index;
        }
        
        // axe le plus etire de l'englobant
        Vector d= Vector(bounds.pmin, bounds.pmax);
        int axis;
        if(d.x > d.y && d.x > d.z)  // x plus grand que y et z ?
            axis= 0;
        else if(d.y > d.z)          // y plus grand que z ? (et que x implicitement)
            axis= 1;
        else                        // x et y ne sont pas les plus grands...
            axis= 2;
        
        // coupe l'englobant au milieu
        float cut= bounds.centroid(axis);
        
        // repartit les triangles 
        Triangle *pm= std::partition(triangles.data() + begin, triangles.data() + end, triangle_less1(axis, cut));
        int m= std::distance(triangles.data(), pm);
        
        // la repartition des triangles peut echouer, et tous les triangles sont dans la meme partie... 
        // forcer quand meme un decoupage en 2 ensembles 
        if(m == begin || m == end)
            m= (begin + end) / 2;
        assert(m != begin);
        assert(m != end);
        
        // construire le fils gauche
        // les triangles se trouvent dans [begin .. m)
        BBox bounds_left= triangle_bounds(begin, m);    // englobant des triangles
        int left= build(bounds_left, begin, m);         // construit le fils gauche 
        
        // on recommence pour le fils droit
        // les triangles se trouvent dans [m .. end)
        BBox bounds_right= triangle_bounds(m, end);     // englobant des triangles
        int right= build(bounds_right, m, end);         // construit le fils droit
        
        // inserer un noeud interne et renvoyer son indice
        int index= nodes.size();
        nodes.push_back( make_node(bounds, left, right) );
        return index;
    }
    // oui, on peut simplifier l'algorithme en virant bounds des parametres, il suffit de recalculer l'englobant des triangles au debut de la fonction, avec triangle_bounds(begin, end)...
    
    
    BBox triangle_bounds( const int begin, const int end )
    {
        BBox bbox= EmptyBox();
        for(int i= begin; i < end; i++)
            bbox.insert(triangles[i].bounds());
        
        return bbox;
    }
};

et voila !! c'est exactement la meme stratégie que tout à l'heure, mais bien sur, il faut conserver les englobants, les groupes d'objet et construire l'arbre en plus.

parcours

Maintenant que l'arbre est construit, il faut l'utiliser pour calculer les intersections d'un rayon et des objets. La encore, le principe est le meme que tout à l'heure, dans la fonction de répartition. Si le rayon touche l'englobant d'un noeud, il faut aussi vérifier s'il touche les englobants des fils du noeud. L'intersection avec les objets ne se fait qu'au niveau des feuilles.

intersection( noeud, rayon ) :
    si le rayon ne touche pas l''englobant du noeud
        arreter
        
    si le noeud est une feuille
        pour chaque objet associé à la feuille
            intersection(objet, rayon)
    sinon
        intersection(fils gauche, rayon)
        intersection(fils droit, rayon)

ce qui s'écrit directement :

struct BVH
{
    ... 
    Hit intersect( const Ray& ray ) const
    {
        Hit hit(ray.tmax);
        intersect(root, ray, hit);
        return hit;
    }
 
protected:
    void intersect( const int index, const Ray& ray, Hit& hit ) const
    {
        const Node& node= nodes[index];
        if(node.bounds.intersect(ray))
        {
            if(node.leaf())
            {
                for(int i= node.leaf_begin(); i < node.leaf_end(); i++)
                    if(Hit h= triangles[i].intersect(ray, hit.t))
                        hit= h;
            }
            else // if(node.internal())
            {
                intersect(node.internal_left(), ray, hit);
                intersect(node.internal_right(), ray, hit);
            }
        }
    }
};

et alors ca marche ??

pour la cornell box, 32 triangles :

• direct() 90ms
• divide() 80ms
• bvh construction < 1ms, construction + intersection 85ms

pour un objet plus gros, par exemple data/bigguy.obj, 3000 triangles :

• direct() 12400ms
• divide() 170ms
• bvh construction < 1ms, construction + intersection 150ms

plus gros, sibenik : 75000 triangles

• direct() abandon...
• divide() 710ms
• bvh construction 19ms, construction + intersection 910ms

sponza version crytek : 250000 triangles

• direct() pas la peine...
• divide() 2470ms
• bvh construction 80ms, construction + intersection 4000ms

musee : 1500000 triangles

• direct() pas la peine...
• divide() 2800ms
• bvh construction 480ms, construction + intersection 4000ms

bien sur, on peut maintenant paralleliser l'intersection des rayons (avec openMP, par exemple) :

#pragma omp parallel for schedule(dynamic, 1024)
for(int i= 0; i < int(rays.size()); i++)
    bvh.intersect(rays[i]);

sur 6 coeurs / 12 threads : le temps de construction du bvh ne change pas, par contre voici les temps d'intersection :

• sibenik : intersection 120ms (au lieu de 900ms)
• sponza version crytek : intersection 450ms (au lieu de 4000ms )
• musée : intersection 310ms (au lieu de 3700ms )

c'est mieux, la construction du bvh et son parcours / intersection parallelisé sont toujours plus rapides que divide() et le bvh sera plus simple à utiliser pour calculer une image.

pour les curieux : la version en ligne de PBRT (un livre de référence sur le lancer rayons et les calculs réalistes) propose également d'utiliser des BVH. 3 méthodes de construction sont présentées, ainsi que l'optimisation de la représentation mémoire de l'arbre et un parcours ordonné plus efficace que celui présenté ici.

paralléliser le calcul de l'image

pour paralléliser le calcul de l'image, il suffit de se rendre compte que le calcul d'un pixel est indépendant des autres pixels, et qu'il suffit de paralleliser la boucle sur les lignes de l'image :

// parcours parallele de toutes les lignes de l'image
#pragma omp parallel for schedule(dynamic, 1)
for(int y= 0; y < image.height(); y++)
for(int x= 0; x < image.width(); x++)
{
    // generer le rayon sur le centre du pixel (x, y)
    Point origine= inv(Point(x + .5f, y + .5f, 0));
    Point extremite= inv(Point(x + .5f, y + .5f, 1));
    Ray ray(origine, extremite);
    
    // calculer la couleur du pixel (x, y)
    { ... }
    
    image(x, y)= Color( ..., 1 );
}

peut mieux faire...

il est possible de construire des arbres de meilleure qualité qui sont encore plus rapide à parcourir (>2 fois !!), mais ce sera pour le cours de M2...