9.2. Solution par éléments finis en 1D#
cours master M1 mécanique: éléments finis (Marc Buffat , UCB Lyon 1)
%matplotlib inline
# bibliothéque
import sys,os
import numpy as np
import scipy as sp
import matplotlib
import matplotlib.pyplot as plt
from random import random
from validation.validation import check_function
from IPython.display import display, Markdown, Latex
def printmd(string):
display(Markdown(string))
# test si numero étudiant spécifier
try: NUMERO_ETUDIANT
except NameError: NUMERO_ETUDIANT = None
if type(NUMERO_ETUDIANT) is not int :
# printmd("## ERREUR: numéro d'étudiant non spécifié!!!")
NUMERO_ETUDIANT = 12345
NOM = "test"
PRENOM = "test"
# parametres spécifiques
_uid_ = NUMERO_ETUDIANT
_precis_ = 1.0e-5
_a_ = sum([int(c) for c in str(_uid_)])/len(str(_uid_))
_b_ = max([int(c) for c in str(_uid_)])
printmd("## Etudiant {} {} id:{} précision des calculs:{}".format(NOM,PRENOM,_uid_,_precis_))
printmd("### paramêtres: a={} b={}".format(_a_,_b_))
Etudiant test test id:12345 précision des calculs:1e-05
paramêtres: a=3.0 b=5
9.2.1. Equation de Laplace#
On veut calculer une solution approchée par éléments finis P1 de l’équation suivante:
avec des conditions aux limites de Dirichlet homogène.
On cherche une solution approchée \(u_h(x)\) par éléments finis \(P^1\)
La formulation éléments finis conduit à la résolution d’un système linéaire
Les valeurs des paramètres a et b sont les suivantes:
print("valeur des coefficients a=",_a_,"b=",_b_)
valeur des coefficients a= 3.0 b= 5
9.2.2. Calcul de la matrice élémentaire#
Ecrire une fonction qui calcule la matrice élémentaire et une fonction qui calcule le second membre élémentaire pour un élément de longueur h. On doit retourner des tableaux numpy.
9.2.2.1. code python#
def MatriceElementaire(h):
'''matrice elementaire pour un elt de longueur h'''
### BEGIN SOLUTION
Me = _a_/h*np.array([[1.,-1],[-1.,1.]])
return Me
### END SOLUTION
def SecondMbElementaire(h):
'''second membre pour un elt de longueur h'''
### BEGIN SOLUTION
Be = _b_*h*np.array([1./2,1./2])
return Be
### END SOLUTION
9.2.2.2. vérification et validation#
on affiche le résultat pour un élèment de longueur 0.1
print('Ae=',MatriceElementaire(0.1))
print('Be=',SecondMbElementaire(0.1))
Ae= [[ 30. -30.]
[-30. 30.]]
Be= [0.25 0.25]
# tests de validation
assert(check_function(MatriceElementaire,"exo250",_a_))
assert(check_function(SecondMbElementaire,"exo251",_b_))
print('Validation OK')
Validation OK
9.2.3. Assemblage et second membre#
Pour un maillage de N éléments équidistants, écrire une fonction pour calculer par assemblage la matrice globale (avant conditions aux limites) et le second membre. On utilisera les 2 fonctions précédentes.
9.2.3.1. code python#
def Matrice(N):
'''matrice elts finis pour N elts'''
### BEGIN SOLUTION
h = 2.0/N
A = np.zeros((N+1,N+1))
for k in range(N):
A[k:k+2,k:k+2] += MatriceElementaire(h)
return A
### END SOLUTION
def SecondMb(N):
'''second membre elts finis pour N elts'''
### BEGIN SOLUTION
h = 2.0/N
B = np.zeros((N+1))
for k in range(N):
B[k:k+2] += SecondMbElementaire(h)
return B
### END SOLUTION
9.2.3.2. vérification et validation#
Résultat pour un maillage de 2 elements
print('A=',Matrice(2),'\nB=',SecondMb(2))
A= [[ 3. -3. 0.]
[-3. 6. -3.]
[ 0. -3. 3.]]
B= [2.5 5. 2.5]
# verification que les fonctions utilises bien MatriceElementaire et SecondMbElementaire
MatriceElementaire_org = MatriceElementaire
SecondMbElementaire_org = SecondMbElementaire
del MatriceElementaire, SecondMbElementaire
try:
Matrice(2)
SecondMb(2)
except NameError:
print('Validation OK')
pass
else:
raise AssertionError(' n utilise pas MatriceElementaire / SecondMbElementaire')
finally:
MatriceElementaire = MatriceElementaire_org
SecondMbElementaire = SecondMbElementaire_org
Validation OK
# test de validation
assert(check_function(Matrice, "exo252",_a_))
assert(check_function(SecondMb,"exo253",_b_))
print('Validation OK')
Validation OK
9.2.4. Calcul solution approchée#
Ecrire une fonction qui calcul la solution approchée sur un maillage de N éléments et qui utilise les fonctions précédentes
def Solution(N):
'''calcul la solution approchée avec N elts'''
### BEGIN SOLUTION
A = Matrice(N)
B = SecondMb(N)
# cdts aux limites
A[0,:]=0.; A[:,0]=0.; A[0,0]=1.; B[0]=0.
A[-1,:]=0.; A[:,-1]=0.; A[-1,-1]=1.; B[-1]=0.
# resolution
X = np.linalg.solve(A,B)
return X
### END SOLUTION
9.2.4.1. vérification et validation#
Résultats pour un maillage de 4 éléments
print("Solution X=",Solution(4))
Solution X= [0. 0.625 0.83333333 0.625 0. ]
# verification que la fonction utilise bien Matrice et SecondMb
Matrice_org = Matrice
SecondMb_org = SecondMb
del Matrice,SecondMb
try:
Solution(2)
except NameError:
print('Validation OK')
pass
else:
raise AssertionError('Solution n utilise pas Matrice et SecondMb')
finally:
Matrice = Matrice_org
SecondMb = SecondMb_org
Validation OK
# test de validation
assert(check_function(Solution,"exo254",[_a_,_b_]))
print('Validation OK')
Validation OK
9.2.5. Interpolation P1#
écrire une fonction calculant la solution approchée Uh calculée sur un maillage de N éléments en un point x quelconque du domaine.
def interpolP1(Uh,x):
'''calcul la valeur de Uh en x (Uh est le tableau des valeurs nodales)'''
### BEGIN SOLUTION
N = Uh.size-1
h = 2./N
Xh = np.linspace(-1,1,N+1)
k = np.searchsorted(Xh,x)
alpha = (Xh[k]-x)/h
val = Uh[k]
if k>0 and k<=N:
val = (1.-alpha)*Uh[k] + alpha*Uh[k-1]
return val
### END SOLUTION
9.2.5.1. validation et verification#
affiche la valeur de la solution pour 2 elts
N=2
Uh = Solution(N)
print("Uh=",Uh)
for x in np.linspace(-1,1,2*N+1):
print("x=",x," uh=",interpolP1(Uh,x))
Uh= [0. 0.83333333 0. ]
x= -1.0 uh= 0.0
x= -0.5 uh= 0.4166666666666667
x= 0.0 uh= 0.8333333333333334
x= 0.5 uh= 0.4166666666666667
x= 1.0 uh= 0.0
# test de validation
assert(check_function(interpolP1,"exo255",[_a_,_b_]))
print('Validation OK')
Validation OK
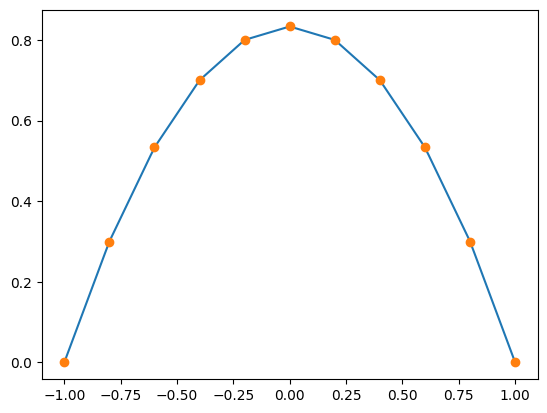
Tracer sur un même graphe la solution Uh et son interpolation sur 100 points
### BEGIN SOLUTION
N=10
Xh=np.linspace(-1,1,N+1)
Uh=Solution(N)
X=np.linspace(-1,1,100)
U=[interpolP1(Uh,x) for x in X]
plt.plot(X,U)
plt.plot(Xh,Uh,'o')
### END SOLUTION
[<matplotlib.lines.Line2D at 0x7fc0b9040880>]
9.2.6. Calcul erreur#
Ecrire une fonction qui calcule la valeur absolue de l’erreur avec un maillage de N éléments par rapport à la solution exacte \(u_e\) en des points données dans un tableau X. Le résultat est un tableau E de même dimension que X.
def Erreur(N,X):
'''calcul de l erreur avec N elts aux points X du maillage'''
### BEGIN SOLUTION
Uh = Solution(N)
Ui = [interpolP1(Uh,x) for x in X]
Uex = _b_/(2.*_a_)*(1-X**2)
Err = np.abs(Ui-Uex)
return Err
### END SOLUTION
9.2.6.1. verification et validation#
affiche l’erreur pour N=4 sur 20 pts
X=np.linspace(-1,1,21)
print(Erreur(4,X))
[0. 0.03333333 0.05 0.05 0.03333333 0.
0.03333333 0.05 0.05 0.03333333 0. 0.03333333
0.05 0.05 0.03333333 0. 0.03333333 0.05
0.05 0.03333333 0. ]
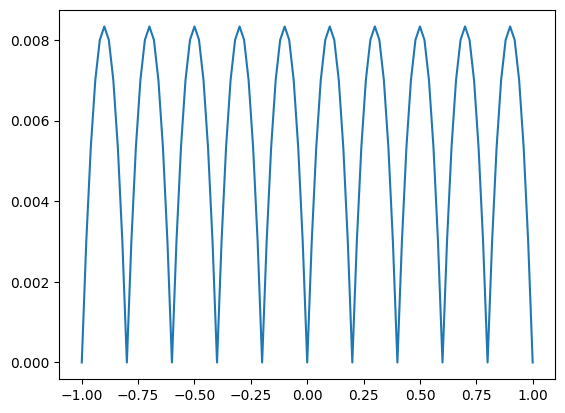
Tracer de l’erreur sur 100 points pour N=10 elements
### BEGIN SOLUTION
N=10
X=np.linspace(-1,1,101)
Err=Erreur(N,X)
plt.plot(X,Err)
### END SOLUTION
[<matplotlib.lines.Line2D at 0x7fc0b871f9a0>]
# test de validation
assert(check_function(Erreur,"exo256",[_a_,_b_]))
print('Validation OK')
Validation OK
9.2.6.2. Calcul de la précision#
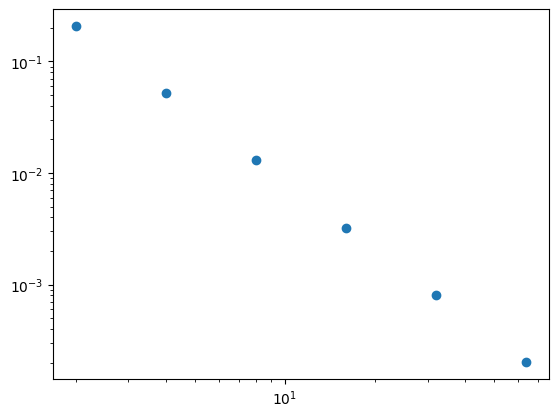
tracer l’évolution de l’erreur max (calculée sur au moins 200 points) en fonction du nombre d’éléments N
### BEGIN SOLUTION
N = [2,4,8,16,32,64]
X = np.linspace(-1,1,201)
Err = np.zeros(len(N))
for i,n in enumerate(N):
Err[i]=np.max(Erreur(n,X))
plt.loglog(N,Err,'o')
pente=np.polyfit(np.log(N),np.log(Err),deg=1)[0]
print("ordre = {:.2}".format(-pente))
### END SOLUTION
ordre = 2.0
9.2.7. conclusion#
écrire vos conclusions (en particulier sur la précision)
=== BEGIN ANSWER ===
=== END ANSWER ===
