8.4. Modélisation EF d’une plaque en traction

Marc BUFFAT, dpt mécanique, Université Claude Bernard Lyon 1

Mise à disposition selon les termes de la Licence Creative Commons
Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 2.0 France.

%matplotlib inline
%autosave 300
from  numpy import *
import matplotlib.pyplot as plt
from IPython.core.display import HTML

Autosaving every 300 seconds

On considère le problème de calcul en contrainte plane d’une plaque rectangulaire \(L\times H\) encastrée à une extrémité et soumis à des efforts extérieurs \(\overrightarrow{F}\)

8.4.1. Mise en equation

Les équations d’équilibre d’un solide soumis à des contraintes planes s’écrivent:

\[ \frac{\partial\sigma_{x}}{\partial x}+\frac{\partial\tau_{xy}}{\partial y}=0 \]

\[ \frac{\partial\sigma_{y}}{\partial y}+\frac{\partial\tau_{xy}}{\partial x}=0 \]

où \(\sigma\) est le tenseur des contraintes, qui est lié au taux de déformation \(\varepsilon\) à travers la loi de comportement. Soient \((u,v)\) les déplacements, on a donc:

\[\begin{split} \overrightarrow{\varepsilon}=\left[\begin{array}{c} \varepsilon_{x}\\ \varepsilon_{y}\\ \gamma_{xy} \end{array}\right]=\left[\begin{array}{c} \frac{\partial u}{\partial x}\\ \frac{\partial v}{\partial y}\\ \frac{\partial u}{\partial y}+\frac{\partial v}{\partial x} \end{array}\right]\,\,,\,\,\sigma=\left[\begin{array}{c} \sigma_{x}\\ \sigma_{y}\\ \tau_{xy} \end{array}\right] \end{split}\]

avec la loi de comportement de l’élasticité linéaire pour un problème de contraintes planes, où \(E\) est le module d’élasticité du matériau et \(\nu\) le coefficient de Poisson.:

\[\begin{split} \overrightarrow{\sigma}=D.\overrightarrow{\varepsilon}\,\mbox{ avec }D=\frac{E}{1-\nu^{2}}\left[\begin{array}{ccc} 1 & \nu & 0\\ \nu & 1 & 0\\ 0 & 0 & \frac{1-\nu}{2} \end{array}\right] \end{split}\]

Les conditions aux limites sont :

1. déplacements fixés: \(u=0, v=0\) en \(x=0\) (frontière \(\Gamma_{0}\))

2. contraintes imposées: \(\sigma_{x}.n_{x}=F\) ou \(\tau_{xy}.n_{x}=0\) en \(x=L\) (frontière \(\Gamma_{1}\))

3. frontières libres en \(y=0\) et \(y=H\)

8.4.2. Formulation faible (exercice)

Ecrire la formulation faible du problème et montrez que l’on peut l’écrire sous forme matricielle

\[ \int_\Omega {\overrightarrow{\sigma} . \overrightarrow{\delta \varepsilon} \, d\Omega } = \int_\Gamma {\overrightarrow{F}. \delta \overrightarrow{u}} \, d\Gamma \]

En déduire la formulation variationnelle

8.4.3. Formulation variationnelle

L’énergie totale du système s’écrit:

\[ E=\frac{1}{2}\int_{\Omega}\overrightarrow{\sigma}.\overrightarrow{\varepsilon}\, d\Omega=\frac{1}{2}\int_{\Omega}\{\varepsilon\}^{t}.D\{\varepsilon\}\, d\Omega \]

et le travail des forces extérieures (sur \(\Gamma_{1}\)) partie de la frontière de \(\Omega\) où on impose une contrainte \(F\) (\(\Gamma=\partial\Omega=\Gamma_{1}+\Gamma_{0}\))

\[ W=\int_{\Gamma_{1}}\{\overrightarrow{u}\}^{t}\{\overrightarrow{F}\}\, d\Gamma \]

La solution équilibre \(\overrightarrow{u}=(u,v)\) est obtenu lorsque l’énergie potentielle totale \(L=E-W\) est minimale pour tous les déplacements virtuels licites (i.e. vérifiant les conditions aux limites cinématiques)

\[\begin{split} \begin{eqnarray} L&=&\frac{1}{2}\int_{\Omega}\{\frac{\partial u}{\partial x},\frac{\partial v}{\partial y},\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\}^{t}.D\{\frac{\partial u}{\partial x},\frac{\partial v}{\partial y},\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\}\, d\Omega\\ &-&\int_{\Gamma_{1}}\{u\, v\}^{t}\{F\}\, d\Gamma \end{eqnarray} \end{split}\]

L’énergie potentiel \(L(u,v)\) est minimale si sa variation \(\delta L\) est nulle pour toute variation \((\delta u,\delta v)\) de \((u,v)\) licites, i.e.:

\[ \delta L=(\frac{\delta L}{\delta u}).\overrightarrow{\delta u}=0\,\,\forall\,\overrightarrow{\delta u}_{\Gamma_{0}}=0 \]

soit

\[ \int_{\Omega}\{\frac{\partial\delta u}{\partial x},\frac{\partial\delta v}{\partial y},\frac{\partial\delta u}{\partial y}+\frac{\partial\delta v}{\partial x}\}^{t}.D\{\frac{\partial u}{\partial x},\frac{\partial v}{\partial y},\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\}\, d\Omega=\int_{\Gamma_{1}}\{\delta u\,\delta v\}^{t}\{F\}\, d\Gamma\,\,\forall\overrightarrow{\delta u}=\{\delta u,\delta v\}\, \mbox{ t.q. } v_{\Gamma_{0}}=0 \]

8.4.4. Approximation par éléments finis

Soit \(T^{h}\) une triangulation de \(\Omega\) associé à une approximation \(P^{1}\). Soient \(n_{e}\) le nombre de triangles, \(nn\) le nombre total de noeuds, et \(n_{0}\) le nombre de noeuds sur la frontière \(\Gamma_{0}\)

Le nombre de ddl du problème est \(2(nn-n_{0})=2.n_{1}\) et en notant \(\phi_{i}\) la base E.F. on a:

\[ u(x,y)=\sum_{i=1}^{n_{1}}U_{i}\Phi_{i}(x,y)\,,\, v(x,y)=\sum_{i=1}^{n_{1}}V_{i}\Phi_{i}(x,y) \]

Les variations \(\delta \overrightarrow{u}\) associées sont pour chaque noeud i:

\[ \delta \overrightarrow{u}=\{\Phi_{i},0\}\,\, et\,\,\delta \overrightarrow{u}=\{0,\Phi_{i}\}\]

et le système de \(2n_1\) équations s’écrit:

\[\begin{split} \begin{eqnarray} \int_{\Omega}\{\frac{\partial\Phi_{i}}{\partial x},0,\frac{\partial\Phi_{i}}{\partial y}\}^{t}.D\{\frac{\partial u}{\partial x},\frac{\partial v}{\partial y},\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\}\, d\Omega &=& \int_{\Gamma_{1}}\{\Phi_{i}\,0\}^{t}\{T\}\, d\Gamma\,\forall i=1,n_{1}\\ \int_{\Omega}\{0,\frac{\partial\Phi_{i}}{\partial y},\frac{\partial\Phi_{i}}{\partial x}\}^{t}.D\{\frac{\partial u}{\partial x},\frac{\partial v}{\partial y},\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\}\, d\Omega &=& \int_{\Gamma_{1}}\{0\,\Phi_{i}\}^{t}\{T\}\, d\Gamma\,\forall i=1,n_{1} \end{eqnarray} \end{split}\]

8.4.4.1. Fonctions de Forme

Sur un element \(l\), de sommets \(\{P_{1},P_{2},P_{3}\}\), l’approximation élément finis s’écrit en fonction de 3 fonctions de forme \(N_p(x,y)\) des des valeurs aux 3 sommets \((n_1,n_2,n_3)\):

\[\begin{split} \begin{eqnarray} u(x,y) &=& u_{n_1}N_{1}(x,y)+u_{n_2}N_{2}(x,y)+u_{n_3}N_{3}(x,y)\\ v(x,y) &=& v_{n_1}N_{1}(x,y)+v_{n_2}N_{2}(x,y)+v_{n_3}N_{3}(x,y) \end{eqnarray} \end{split}\]

Les fonctions de forme de l’élément \(\{N_{1}(x,y),N_{2}(x,y),N_{3}(x,y)\}\) vérifient les conditions:

\[ N_{i}(P_{j})=\delta_{i,j}\,\forall i,j=1,3\]

La fonction \(N_{1}(x,y)\) a pour expression:

\[ N_{1}(x,y)=\frac{a_{1}x+b_{1}y+c_{1}}{2Aire} \]

avec

\[a_{1}=Y_{2}-Y_{3}\,,\, b_{1}=X_{3}-X_{2}\,,\, c_{1}=X_{2}Y_{3}-X_{3}Y_{2}\]

Les autres sont obtenues par permutation circulaire.

L’aire du triangle est égale à

\[ aire=\frac{a_{1}+a_{2}+a_{3}}{2}=0.5*((X_{2}-X_{1})(Y_{3}-Y_{1})-(X_{3}-X_{1})(Y_{2}-Y1)) \]

Le gradient \(\nabla N_1\) de \(N_1\) est constant et s’écrit

\[\nabla N_{1}=\{\frac{a}{2aire},\frac{b}{2aire}\}\]

8.4.5. Matrice et second membre élémentaire

Sur un élément, le déplacement \(\{\overrightarrow{u}\}\) s’écrit

\[\begin{split} \left[\begin{array}{c} u\\ v \end{array}\right]=\left[\begin{array}{cccccc} N_{1} & 0 & N_{2} & 0 & N_{3} & 0\\ 0 & N_{1} & 0 & N_{2} & 0 & N_{3} \end{array}\right]\,\{U\}\,\mbox{ avec }U=\left[\begin{array}{c} u_{n_1}\\ v_{n_1}\\ u_{n_2}\\ v_{n_2}\\ u_{n_3}\\ v_{n_3} \end{array}\right] \end{split}\]

Le taux de déformation \(\{\overrightarrow{\varepsilon}\}\) sur un élément s’écrit

\[\begin{split} \left[\begin{array}{c} \frac{\partial u}{\partial x}\\ \frac{\partial v}{\partial y}\\ \frac{\partial u}{\partial y}+\frac{\partial v}{\partial x} \end{array}\right]=[B].\{U\}\ \end{split}\]

avec

\[\begin{split}B=\left[\begin{array}{cccccc} \frac{\partial N_{1}}{\partial x} & 0 & \frac{\partial N_{2}}{\partial x} & 0 & \frac{\partial N_{3}}{\partial x} & 0\\ 0 & \frac{\partial N_{1}}{\partial y} & 0 & \frac{\partial N_{2}}{\partial y} & 0 & \frac{\partial N_{3}}{\partial y}\\ \frac{\partial N_{1}}{\partial y} & \frac{\partial N_{1}}{\partial x} & \frac{\partial N_{2}}{\partial y} & \frac{\partial N_{2}}{\partial x} & \frac{\partial N_{3}}{\partial y} & \frac{\partial N_{3}}{\partial x} \end{array}\right] \end{split}\]

d’ou la contrainte \(\{\overrightarrow{\sigma}\}\)

\[\{\overrightarrow{\sigma}\}=[D]\{\overrightarrow{\varepsilon}\}=[D][B]\{U\}\]

8.4.5.1. Matrice élémentaire

La matrice de rigidité du système est donc la matrice 6*6

\[[K_{e}]=\int_{e}[B]^{t}[D][B]\, d\Omega\]

Pour un élément triangulaire la matrice \([B]\) est constante et la matrice élémentaire \(K^{e}\) s’écrit:

\[K_{e}=[B]^{t}[D][B]*Aire\]

8.4.5.2. Second membre élémentaire

Le vecteur second membre élémentaire \(B^{e}\) n’apparait que sur les éléments ayant un coté sur \(\Gamma_{1}\).

Soient \(\{n_{1},n_{2}\}\) les 2 sommets de l’élément sur la frontière (dans le sens trigonométrique), les intégrales de bord s’écrivent:

\[\begin{split} \begin{eqnarray} B_{2j-1}^{e}&=&\int_{P_{1}}^{P_{2}}F_{x}\Phi_{j}ds=F_{x}\frac{L}{2}\,\,\forall j=1,2\\ B_{2j}^{e}&=&\int_{P_{1}}^{P_{2}}F_{y}\Phi_{j}ds=F_{y}\frac{L}{2}\,\,\forall j=1,2 \end{eqnarray} \end{split}\]

Le vecteur \(B^{e}\) est donc de dimension 4.

8.4.6. Assemblage

Algorithme d’assemblage de la matrice A

Algorithme

A=0
pour l de 1 à Ne # boucle sur les elements
  # calcul de la matrice élémentaire 6*6 Ke
  Pour i de 1 à 3    
     Pour j de 1 à 3     
        ni=Tbc[l,i] 
        nj=Tbc[l,j]  # numerotation globale 
        A[2*ni-1,2*nj-1]=Ke[2i-1,2j-1]
        A[2*ni-1,2*nj]  =Ke[2i-1,2j]
        A[2*ni,2*nj-1]  =Ke[2i,2j-1]
        A[2*ni,2*nj]    =Ke(2i,2j)
     Fin j
   Fin i
Fin l

Les conditions aux limites sont de 2 types:

1. Dirichlet: on fixe la valeur du déplacement dans le \(2^{nd}\)menbre, on annulle la ligne correspondante dans la matrice A, et on fixe la diagonale à 1

2. Neuman: on calcul la contribution des intégrales de bord dans le second membre

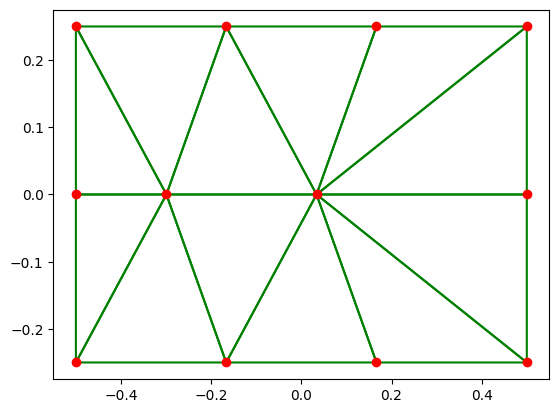
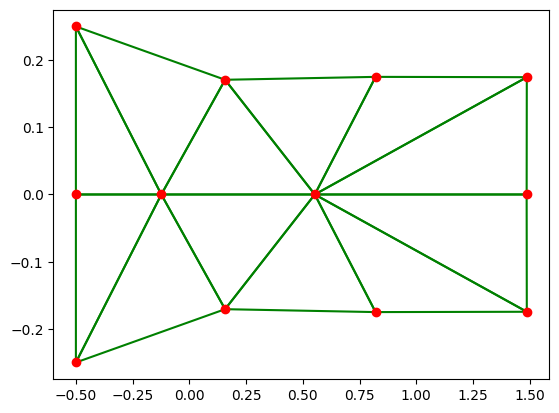
8.4.7. Exécution code Python

%run plaque.py

Maillage nom  plaque.msh
Nn,Ne= 12 12
Xmin/max Ymin/max= -0.5 0.5 -0.25 0.25
Verification calcul gradient 
surface  0.4999999999999999  err= 8.881784197001252e-16 0.0
Verification assemblage  6.4373016357421875e-06 1.341104507446289e-05
U= (12,) 0.0 9.871523126485717e-08 1e-07
V= (12,) -7.931238146249413e-09 7.93123818567599e-09 7.5e-09

<Figure size 640x480 with 0 Axes>

8.4.8. Fin