Approximation spectrale (formulation faible)

8.1. Approximation spectrale (formulation faible)#

Marc Buffat , dpt mécanique, Lyon 1

8.1.1. Problème#

On considère le problème de recherche une fonction \(u(x)\) solution de

(8.1)#\[\begin{equation} -\frac{\partial^{2}u}{\partial x^{2}}=f(x)\,\mbox{ dans }\Omega=[0,1] \end{equation}\]

avec \(f(x)\) une fonction connue et les conditions aux limites:

(8.2)#\[\begin{equation} u(0)=0,\,\,u(1)=0 \end{equation}\]

8.1.1.1. Formulation faible#

Trouver la fonction \(u(x)\) t.q. : \(u(0)=0,\,\,u(1)=0\)

\[ \int_{0}^{1}\frac{\partial u}{\partial x}\frac{\partial v}{\partial x}\,dx=\int_{0}^{1}f.v\,dx\,\,\forall v(x) \]

qui doit être vérifiée quelque soit la fonction test \(v(x)\) t.q. \(v(0)=0,\,\,v(1)=0\)

8.1.1.2. Approximation#

  1. choix d’une base de N fonctions de base \({\phi_{i}}_{i=1,N}\) vérifiant les conditions sur \(u(x)\)

\[ \phi_{i}(0)=\phi_{i}(1)=0 \]

  1. recherche d’une approximation sur cette base \({\phi_{i}}\)

\[u^{h}(x)=\sum_{j=1}^{N}a_{j}\phi_{j}(x)\]

  1. les inconnues sont les N coefficients: $\({a_i}_{i=1,N}\)$

  2. calcule de la variation \(v = \delta u\)

\[ v^h = \delta u^h = \sum_{i=1}^{N}\delta a_{i}\phi_{i}(x)\]

  1. choix des fonctions tests (Galerkin) \(\forall v^h\) \(\Rightarrow\)

\[v_h(x) = \phi_{i}(x) \mbox{ pour } i=1,N \]

8.1.1.3. Equations discrètes#

en remplaçant \(u\) par \(u^h\)

\[u^{h}(x)=\sum_{j=1}^{N}a_{j}\phi_{j}(x)\]

et \(v\) par \(v^h\)

\[v_h(x) = \phi_{i}(x) \mbox{ pour } i=1,N \]

\(\Rightarrow\) N équations pour N inconnues \({a_j}\)

  • pour \(i=1,N\)

\[ \sum_{j=1,N} a_j \int_{0}^{1}\frac{\partial \phi_j}{\partial x}\frac{\partial \phi_i}{\partial x}\,dx=\int_{0}^{1}f.\phi_i\,dx\, \]

  • soit le système linéaire

\[ A X = B \mbox{ avec } X = [a_j]_{j=1,N}\]

avec

\[ A_{i,j} = \int_{0}^{1}\frac{\partial \phi_j}{\partial x}\frac{\partial \phi_i}{\partial x}\,dx\]

et

\[ B_i = \int_{0}^{1}f.\phi_i\,dx\,\]

8.1.2. Approximation spectrale#

On choisit comme base : $\(\phi_i(x) = \sin(i\pi x)\)$

propriétés

  • vérifie les CL \(\phi_i(0)=\phi_j(0)=0\)

  • calcul analytique de certaines intégrales

\[ \int_0^1 \phi_i(x) ^2\, dx = \frac{1}{2} \]
\[ \int_0^1 \phi_i(x) \phi_j(x)\, dx =0 \mbox{ si } i \neq j\]

  • sinon calcul numérique des intégrales

intégration numérique

  • méthode des trapèzes, simpson (simple mais peu précise si peu de points)

  • méthode des points de Gauss (méthode beaucoups plus précise)

Avec \(n_g\) points de Gauss sur \([-1, 1]\),on a :

\[ \int_{-1}^{+1} F(x)\,dx \approx \sum_{i=1}^{n_g} \omega_i F(x_i) \]

problème: évaluation en des points non régulièrement espacés !

fonctions python dans scipy:

  • nbre de points de quadrature fixe

    scipy.integrate.fixed_quad(func, a, b, args=(), n=5,..)

  • méthode adaptative

    scipy.integrate.quad(func, a, b, args=(),..)

8.1.3. Résolution numérique#

choix de la fonction \(f(x)\)

# bibliothéque
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
plt.rc('font', family='serif', size='16')

# parametres du problème
# choix du second membre
# fonction périodique (convergence spectrale)
f = lambda x: np.exp(-((x-0.5)/0.1)**2)
# non périodique (convergence plus lente)
#f = lambda x: np.exp(x)
# solution analytique
#f = lambda x: 4*np.pi**2*np.sin(2*np.pi*x)

# calcul des coeffients a_i de la solution pour N fct de bases
from scipy.integrate import quad, fixed_quad
def solution(N):
    a  = np.zeros(N)
    ng = 10*N
    for i in range(1,N+1):
        # coefficients matrice
        Aii = 0.5*(i*np.pi)**2
        # et second membre
        F   = lambda x: f(x)*np.sin(i*np.pi*x)
        #Fi  = fixed_quad(F,0,1,n=ng)
        Fi  = quad(F,0,1)
        # solution
        a[i-1] = Fi[0]/Aii
    #
    return a

# calcul solution approchée avec N points
def uh(x,N):
    a = solution(N)
    n = a.size
    val = np.zeros(x.size)
    for i in range(1,n+1):
        val += a[i-1]*np.sin(i*np.pi*x)
    return val

# test
X  = np.linspace(0,1,100)
N  = 5
a  = solution(N)
print("solution:",a)
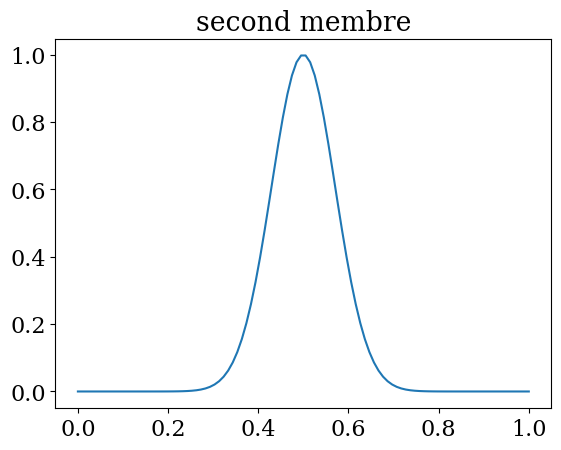
plt.plot(X,f(X))
plt.title("second membre")

solution: [ 3.50420415e-02  8.28876387e-19 -3.19610174e-03 -3.87101401e-19
  7.75301291e-04]

Text(0.5, 1.0, 'second membre')
../../_images/d909fa27da432243f7e9d78383e15efdb34acc4d95a154dbe77ce45b6d304a43.png 
plt.figure(figsize=(12,8))
Y1 = uh(X,1)
plt.plot(X,Y1,label="N=1")
Y3 = uh(X,3)
plt.plot(X,Y3,label="N=3")
Y5 = uh(X,5)
plt.plot(X,Y5,label="N=5")
Y10 = uh(X,10)
plt.plot(X,Y10,label="N=10")
Y20 = uh(X,20)
plt.plot(X,Y20,label="N=20")
plt.legend()
plt.xlabel('$x$')
plt.ylabel('$u_h(x)$')
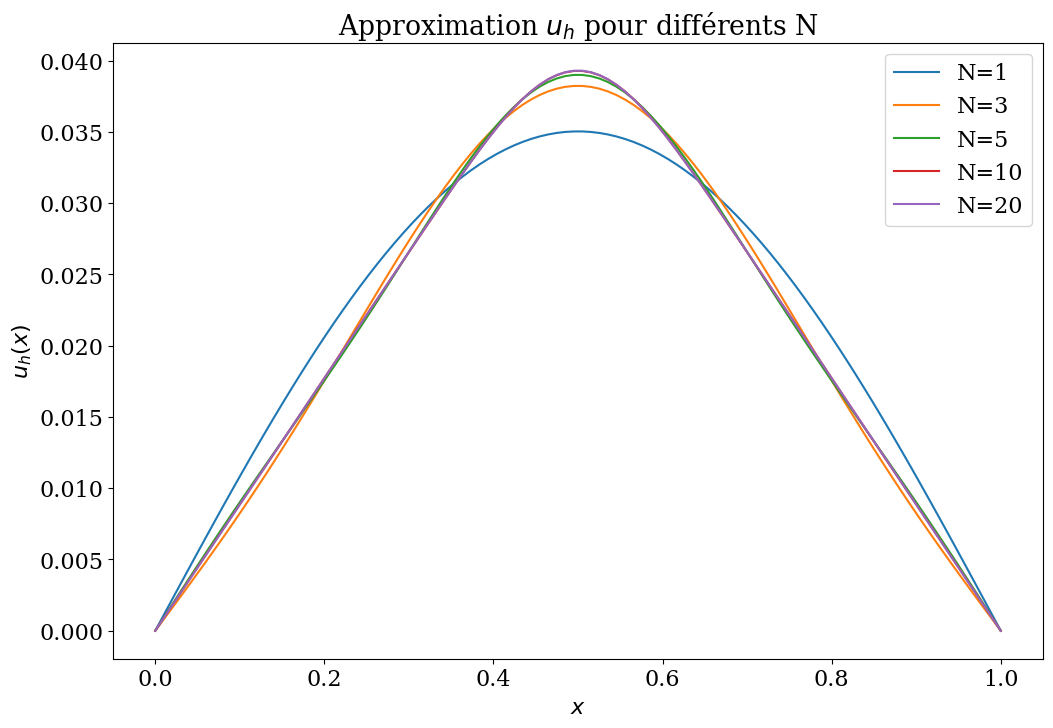
plt.title("Approximation $u_h$ pour différents N");
../../_images/ecd96d2fbd5c6ddb8b1a00e14a87caccacffe00bdfe2c17a92b9d3b220c87d53.png 
plt.figure(figsize=(12,8))
plt.plot(X,Y1-Y20,label="N=1")
plt.plot(X,Y3-Y20,label="N=3")
plt.plot(X,Y5-Y20,label="N=5")
plt.plot(X,Y10-Y20,label="N=10")
plt.legend()
plt.xlabel('$x$')
plt.ylabel('$u_h(x)$')
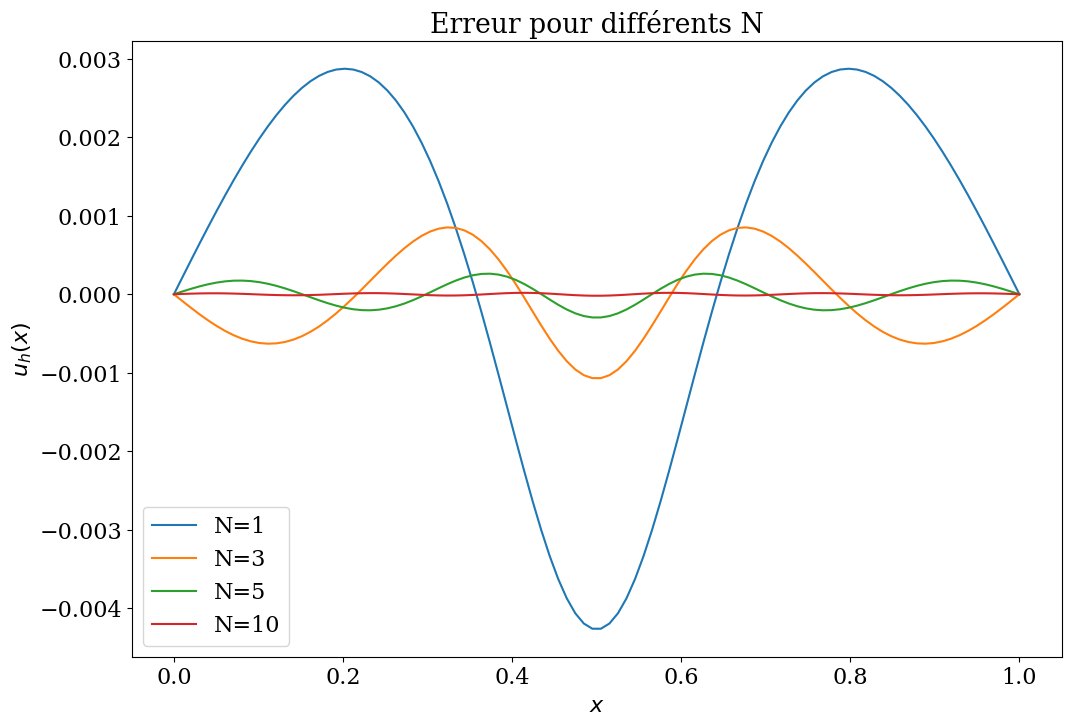
plt.title("Erreur pour différents N");
../../_images/bb29c2712480bf1bc01d44848d3aeee078127f1bcffd05d010dc23cb23732ae2.png 
from numpy.linalg import norm
err1 = norm(Y1-Y20)
err3 = norm(Y3-Y20)
err5 = norm(Y5-Y20)
err10 = norm(Y10-Y20)
NN = [1,3,5,10]
ERR= [err1,err3,err5,err10]
plt.figure(figsize=(12,8))
plt.loglog(NN,ERR,'-o',lw=2)
plt.xlabel('N')
plt.ylabel('$||Err||$')
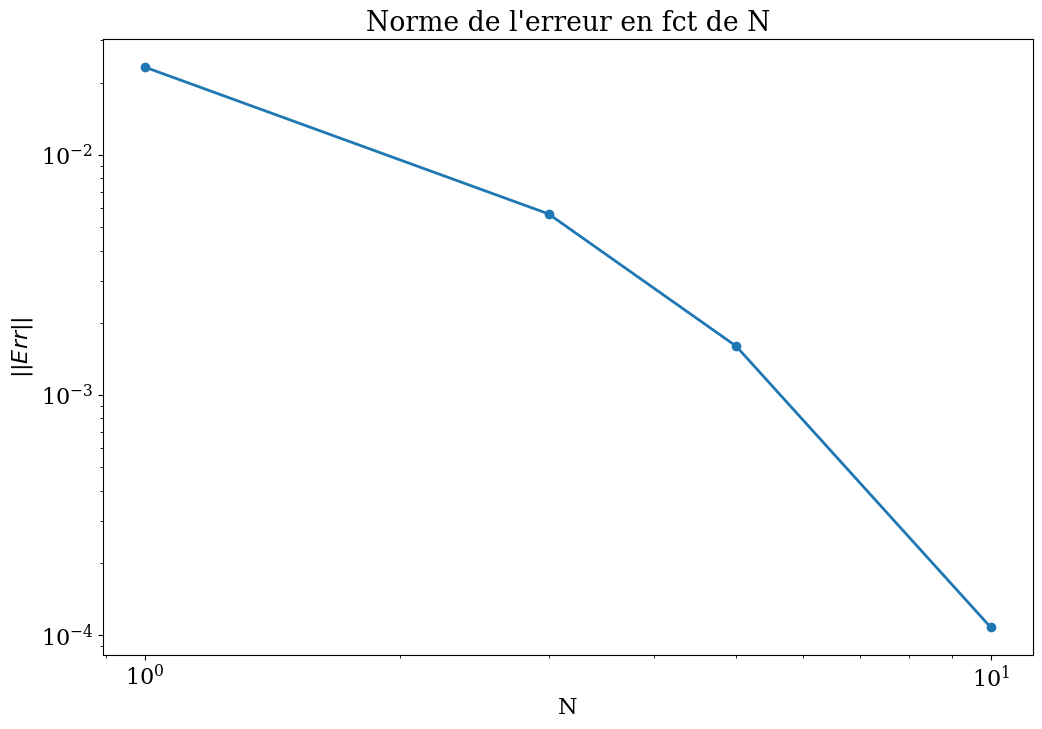
plt.title("Norme de l'erreur en fct de N");
../../_images/3a20f90270b1df24589f28b239885a75aa12edaac3c3364b1697a4fb9369b753.png

8.1.4. Analyse#

  • comment vérifier

  • que peut-on de dire l’erreur (convergence)

  • conclusion

8.1.5. FIN#

Contenu