5. Éléments finis hermitiens

5.1. Problème étudié

On considère une poutre en flexion de longueur L, encastrée en \(x=0\) et soumise à une force de flexion \(F\) en \(x=L\).

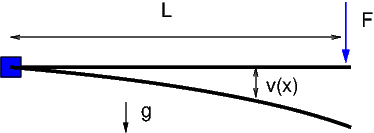
Fig. 5.1 poutre en flexion

On note \(v(x)\) le déplacement transverse, \(\rho\) la masse volumique , \(S\) la section de la poutre, \(E\) le module d’Young, \(I_{zz}\) l’inertie de la section suivant z (perpendiculaire au plan). Avec l’hypothèse d’Euler Bernoulli (un plan normal à la ligne centrale reste normal à cette ligne après déformation), l’angle \(\theta(x)\) de rotation du plan (suivant z) s’écrit:

\[\theta(x)=\frac{dv}{dx}\]

Dans une section, la résultante des contraintes est un torseur, qui comprend la résultante des contraintes de cisaillement \(V_{y}=-EI_{zz}\frac{d^{3}v}{dx^{3}}\) et le moment fléchissant (moment des contraintes normales) \(M_{z}=EI_{zz}\frac{d^{2}v}{dx^{2}}\) . L’équation d’équilibre résulte de l’équilibre du torseur des forces dans une section:

\[\frac{dV_{y}}{dx}-\rho gS=0\,\,\,,\,\,\,\,\frac{dM_{z}}{dx}+V_{y}=0\]

et s’écrit, en notant \(q=-\rho gS\) la force linéique appliquée dans une section:

(5.1)\[\frac{d^{2}}{dx^{2}}(EI_{zz}\frac{d^{2}v}{dx^{2}})=q\]

Les conditions aux limites sont des conditions d’encastrement en \(x=0\)

(5.2)\[v(0)=0\,,\,\theta(0)=0\]

et des conditions dynamiques de force et de moment appliqués en \(x=L\)

(5.3)\[V_{y}(L)=F\,\,,\,\,M_{z}(L)=0\]

Pour obtenir la formulation faible, on applique le théorème des travaux virtuels en calculant le travail du système pour un déplacement virtuel licite \(w\) (variation du déplacement \(v\)). On obtiens:

\[\int_{0}^{l}\frac{d^{2}}{dx^{2}}(EI_{zz}\frac{d^{2}v}{dx^{2}})w\,dx=\int_{0}^{l}qw\,dx\]

On intègre 2 fois par parties pour symétriser le problème et faire apparaître les conditions aux limites:

\[\int_{0}^{L}EI_{zz}\frac{d^{2}v}{dx^{2}}\frac{d^{2}w}{dx^{2}}\,dx+[EI_{zz}\frac{d^{3}v}{dx^{3}}w-EI_{zz}\frac{d^{2}w}{dx^{2}}\frac{dw}{dx}]_{0}^{L}=\int_{0}^{L}qw\,dx\]

Le déplacement virtuel \(w\) est une variation de \(v\), et doit donc vérifier les liaisons imposées en \(x=0\) (5.2), i.e

\[w(0)=\delta v(0)=0\,\,\mbox{ et }\frac{dw}{dx}(0)=\delta\theta(0)=0\]

Les conditions aux limites (5.3) s’écrivent en fonction de \(v\):

\[-EI_{zz}\frac{d^{3}v}{dx^{3}}(L)=F,\,\,\,EI_{zz}\frac{d^{2}v}{dx^{2}}=0\]

ce qui permet de calculer les intégrales de bord

\[[EI_{zz}\frac{d^{3}v}{dx^{3}}w-EI_{zz}\frac{d^{2}w}{dx^{2}}\frac{dw}{dx}]_{0}^{L}=Fw(L)\]

La formulation faible s’écrit:

(5.4)\[\mbox{Trouvez }v(x)\,\mbox{ t.q. }v(0)=0,\,\frac{dv}{dx}(0)=0\]

\[\int_{0}^{L}EI_{zz}\frac{d^{2}v}{dx^{2}}\frac{d^{2}w}{dx^{2}}\,dx=\int_{0}^{L}qw\,dx+Fw(L)\,\,\forall w\,\,\mbox{ t.q. }w(0)=0,\,\frac{dv}{dx}(0)=0\]

Cette formulation faible traduit l’équilibre entre le travail des forces élastiques internes et le travail des forces appliquées. Le travail des forces internes dérive d’un potentiel élastique, et cette formulation faible possède donc un Lagrangien:

(5.5)\[\mathcal{L}(v)=\underbrace{-\frac{1}{2}\int_{0}^{L}EI_{zz}\left(\frac{d^{2}v}{dx^{2}}\right)^{2}\,dx}_{U}+\underbrace{\left(\int_{0}^{L}qv\,dx+Fv(L)\right)}_{W}\]

qui correspond à la somme de l’énergie potentielle élastique \(U\) et du travail \(W\) des forces extérieures pour le déplacement \(v\). La formulation variationnelle corresponds donc à rendre stationnaire (maximum dans notre cas) de ce Lagrangien:

(5.6)\[\mbox{Trouvez }v(x)\,\,\mbox{ t.q. }v(0)=0,\,\frac{dv}{dx}(0)=0\]

\[\mathcal{L}(v)\ge\mathcal{L}(\mathtt{v})\,\,\forall\mathtt{v}\,\mbox{ t.q. }\mathtt{v}(0)=0,\,\frac{d\mathtt{v}}{dx}(0)=0\]

et la condition de stationnarité conduit aux équations de Lagrange

\[<\frac{\partial\mathcal{L}}{\partial v},\delta v>=0\,\,\forall\delta v\,\mbox{licite}\]

En utilisant la même remarque de dans le chapitre précédent, on peut déterminer la valeur de l’énergie élastique \(U\) à l’équilibre, en choisissant dans la formulation faible comme variation \(w\) le déplacement réel \(v\).

\[U=\frac{1}{2}\int_{0}^{L}EI_{zz}\left(\frac{d^{2}v}{dx^{2}}\right)^{2}\,dx=\frac{1}{2}\int_{0}^{L}qv\,dx+\frac{1}{2}Fv(L)\]

C’est le travail moyen fournit par les forces extérieures pour passer de l’état naturel (sans contrainte) à l’état d’équilibre contraint en augmentant progressivement les forces extérieures de \(0\) à leurs valeurs finales. C’est ce travail fourni par les forces extérieures qui est transformé en énergie élastique. On constate aussi que dans le Lagrangien, le terme de travail des forces extérieures ne correspond pas au travail fournit, mais à un travail virtuel associé au déplacement \(v\) (dans ce cas le travail fournit est en fait égal à la moitié de cette valeur).

La valeur minimum du Lagrangien est égale à l’énergie potentiel élastique \(U\):

\[\mathcal{L}(v)=-U+W=-U+2U=U\]

5.2. Formulation éléments finis

Pour construire une formulation variationnelle discrète à partir de la formulation (5.6) , il faut construire une approximation \(v^{h}\) de la solution exacte, vérifiant les conditions cinématiques (conditions de Dirichlet):

(5.7)\[v^{h}(0)=0,\,\frac{dv^{h}}{dx}(0)=0\]

et telle que l’on puisse calculer le Lagrangien discret associé à (5.5):

(5.8)\[\mathcal{L}(v^{h})=-\frac{1}{2}\int_{0}^{L}EI_{zz}\left(\frac{d^{2}v^{h}}{dx^{2}}\right)^{2}\,dx+\left(\int_{0}^{L}qv^{h}\,dx+Fv^{h}(L)\right)\]

Pour construire cette approximation par éléments finis, on impose les contraintes suivantes:

1. la solution \(v^{h}\) doit être continue ainsi que sa dérivée \(\frac{dv^{h}}{dx}\) sur tout le domaine \(\Omega=[0,L]\)

2. sur chaque élément, la solution est un polynôme

La première condition permet le calcul des intégrales dans (5.8), puisque \(v^{h}\) est \(\mathcal{C}^{1}(\Omega)\) et permet d’imposer les conditions aux limites fortes (5.7). La seconde condition permet de construire une approximation simple. Sur un élément la solution est un polynôme, qui doit vérifier quatre conditions: la continuité de la fonction et de sa dérivée en chacune des deux extrémités de l’élément. C’est donc un polynôme d’Hermite de degré 3. Sur la figure, on a tracer un exemple d’approximation pour un maillage de 2 éléments.

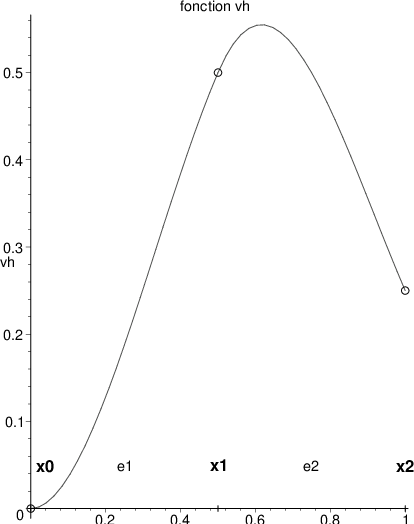
Fig. 5.2 approximation \(v^{h}\) sur un maillage de 2 éléments

D’un point de vue mécanique, on cherche une solution approchée \(v^{h}\) qui fournit une approximation continue du déplacement \(v(x)\) et de l’angle de rotation \(\theta(x)\) (dérivée première de \(v(x)\)), et une approximation par élément (éventuellement discontinue aux noeuds) du moment fléchissant \(M_{z}\) (dérivée seconde de \(v(x)\)) et de la résultante de la contrainte de cisaillement \(V_{y}\) (dérivée troisième de \(v(x)\)).

On construit donc un maillage de \(\Omega\) correspondant à un découpage en \(ne\) éléments:

\[\Omega=\bigcup_{i=1}^{ne}[x_{i-1},x_{i}]\]

soient \(ne+1\) noeuds \({x_{i}}_{i=0..ne}\).

L’approximation utilise deux degré de liberté par noeuds: pour chaque noeud \(i\) de coordonnée \(x_{i}\) ce sont la valeur nodale de la fonction \(v_{i}=v^{h}(x_{i})\) et la valeur nodale de la dérivée \((\frac{dv}{dx})_{i}=\frac{dv^{h}}{dx}(x_{i})\). Cela permet de définir de façon unique l’approximation \(v^{h}\), qui possède donc \(2ne=2nn\) degrés de liberté (les valeurs au noeud \(i=0\) sont imposées par la condition aux limites (5.7). Cette approximation s’écrit comme une combinaison linéaire des valeurs nodales de la fonction et de sa dérivée.

En notant \(\Phi_{i}(x)\) les fonctions de base associées aux valeurs nodales de la fonction \(v_{i}\) et \(\Psi_{i}(x)\) les fonctions de base associées aux valeurs nodales de la dérivée \((\frac{dv}{dx})_{i}\), on écrit:

\[v^{h}(x)=\sum_{i=1}^{nn}v_{i}\Phi_{i}(x)+\sum_{i=1}^{nn}(\frac{dv}{dx})_{i}\Psi_{i}(x)\]

Sur un élément \(e_{k}=[x_{k-1},x_{k}]\), cette approximation s’écrit:

\[v^{h}(x)=v_{k-1}\Phi_{k-1}(x)+(\frac{dv}{dx})_{k-1}\Psi_{k-1}(x)+v_{k}\Phi_{k}(x)+(\frac{dv}{dx})_{k}\Psi_{k}(x)\]

C’est l’unique polynôme de degré \(\le3\), \(p(x)\) qui vérifie:

\[p(x_{k-1})=v_{k-1},\,\,p(x_{k})=v_{k},\,\,\frac{dp}{dx}(x_{k-1})=(\frac{dv}{dx})_{k-1},\,\,\frac{dp}{dx}(x_{k})=(\frac{dv}{dx})_{k}\]

C’est un polynôme d’Hermite de degré 3, d’où le nom d’éléments finis hermitiens que l’on donne à cette approximation.

5.2.1. fonctions de forme

Pour calculer l’approximation sur un élément \(e_{k}\), on se place sur l’élément de référence \([-1,+1]\) (comme dans le chapitre précédent) en effectuant un changement de variable:

(5.9)\[\xi=\frac{2x-x_{k}-x_{k-1}}{x_{k}-x_{k-1}}\]

Sur cet élément de référence, on détermine les 4 fonctions de forme associées, qui sont les polynômes de Hermite de degré 3:

1. \(N_{1}(\xi)\) associée à la valeur nodale au premier noeud (\(\xi=-1\)): i.e. telle que

   \[N_{1}(-1)=1,\,\,N_{1}(1)=0,\,\,\frac{dN_{1}}{d\xi}(-1)=0,\,\,\frac{dN_{1}}{d\xi}(1)=0\]

2. \(N_{2}(\xi)\) associée à la valeur nodale au second noeud (\(\xi=+1\)): i.e. telle que

   \[N_{2}(-1)=0,\,\,N_{2}(1)=1,\,\,\frac{dN_{2}}{d\xi}(-1)=0,\,\,\frac{dN_{2}}{d\xi}(1)=0\]

3. \(H_{1}(\xi)\) associée à la valeur de la dérivée au premier noeud (\(\xi=-1\)): i.e. telle que

   \[H_{1}(-1)=0,\,\,H_{1}(1)=0,\,\,\frac{dH_{1}}{d\xi}(-1)=1,\,\,\frac{dH_{1}}{d\xi}(1)=0\]

4. \(H_{2}(\xi)\) associée à la valeur de la dérivée au second noeud (\(\xi=+1\)): i.e. telle que

   \[H_{2}(-1)=0,\,\,H_{2}(1)=0,\,\,\frac{dH_{2}}{d\xi}(-1)=0,\,\,\frac{dH_{2}}{d\xi}(1)=1\]

L’expression de ces polynômes est obtenue en utilisant les 4 conditions imposées. On obtiens ainsi les expressions suivantes:

(5.10)\[\begin{split}\begin{eqnarray} N_{1}(\xi) & = & (1-\xi)^{2}(\frac{1}{2}+\frac{\xi}{4})\\ H_{1}(\xi) & = & \frac{1}{4}(1-\xi)^{2}(1+\xi)\\ N_{2}(\xi) & = & (1+\xi)^{2}(\frac{1}{2}-\frac{\xi}{4})\\ H_{2}(\xi) & = & -\frac{1}{4}(1+\xi)^{2}(1-\xi) \end{eqnarray}\end{split}\]

Ces fonctions de formes ont tracées sur la figure.

Fig. 5.3 fonctions de forme hermitiennes](CHAP31/fforme.png)

L’approximation \(v^{h}\) sur l’élément de référence s’écrit ( en notant \(h=x_{k}-x_{k-1}\)):

(5.11)\[v^{h}(\xi)=v_{k-1}N_{1}(\xi)+\frac{h}{2}(\frac{dv}{dx})_{k-1}H_{1}(\xi)+v_{k}N_{2}(\xi)+\frac{h}{2}(\frac{dv}{dx})_{k}H_{2}(\xi)\]

On constate donc que les fonctions bases \(\Phi_{k}\) sont égales aux fonctions de formes \(N_{1}\) ou \(N_{2}\), mais que les fonctions de base \(\Psi_{k}\) sont égales à \(\frac{h}{2}H_{1}\) ou \(\frac{h}{2}H_{2}\), car la dérivation dans l’élément de référence (i.e. par rapport à \(\xi\)) n’est pas égale à la dérivation physique (i.e. par rapport à x), et on a la relation:

\[\frac{dv^{h}}{dx}=\frac{dv^{h}}{d\xi}\frac{2}{h}\]

Sur l’élément \(e_{k}\) les fonctions de base s’écrivent:

\[\Phi_{k-1}(x)=N_{1}(\xi),\,\,\Psi_{k-1}=\frac{h}{2}H_{1}(\xi),\,\,\Phi_{k}(x)=N_{2}(\xi),\,\,\Psi_{k}=\frac{h}{2}H_{2}(\xi)\]

5.2.2. Calcul du Lagrangien discret

Pour calculer le Lagrangien discret \(\mathcal{L}(v^{h})\), on décompose les intégrales en une somme sur tous les éléments du maillage:

\[\mathcal{L}(v^{h})=-\frac{1}{2}\sum_{k=1}^{ne}\underbrace{\left(\int_{e_{k}}EI_{zz}\left(\frac{d^{2}v^{h}}{dx^{2}}\right)^{2}\,dx\right)}_{E_{k}}+\sum_{k=1}^{ne}\underbrace{\left(\int_{e_{k}}qv^{h}\,dx\right)}_{W_{k}}+\underbrace{Fv^{h}(L)}_{W_{L}}\]

Ce Lagrangien contiens une somme de termes quadratiques \(E_{k}\), de termes linéaires \(W_{k}\) et un terme de bord \(W_{L}\). Le terme \(E_{k}\) correspond à l’énergie élastique de l’élément \(e_{k}\), \(W_{k}\) au travail des forces linéiques appliquées sur l’élément \(e_{k}\) et le terme de bord \(W_{L}\) au travail de la force appliquée en \(x=L\).

D’un point de vue mécanique, nous avons décomposé le système mécanique (la poutre) en \(ne\) morceaux, puis calculé l’énergie mécanique et le travail des forces externes sur chaque élément, pour ensuite en faire la somme.

5.2.2.1. énergie élastique élémentaire \(E_{k}\)

Sur un élément \(e_{k}\), l’énergie élastique est calculée en effectuant le changement de variable (5.9) vers l’élément de référence et en utilisant l’expression (5.11) de \(v^{h}\):

\[E_{k}=\frac{1}{2}\int_{-1}^{+1}\,EI_{zz}\left(\frac{4}{h^{2}}\frac{d^{2}}{d\xi^{2}}\left(v_{k-1}N_{1}(\xi)+\frac{h}{2}(\frac{dv}{dx})_{k-1}H_{1}(\xi)+v_{k}N_{2}(\xi)+\frac{h}{2}(\frac{dv}{dx})_{k}H_{2}(\xi)\right)\right)^{2}\,\frac{h}{2}d\xi\]

\(E_{k}\) est donc une forme quadratique par rapport aux valeurs nodales \(w^{k}=\left[v_{k-1},\,(\frac{dv}{dx})_{k-1},\,v_{k},\,(\frac{dv}{dx})_{k}\right]^{t}\) qui s’écrit

\[\begin{split}\begin{eqnarray} E_{k} & = & \frac{1}{2}\left(w^{k}\right)^{t}\,\mathbf{K}^{k}\,w^{k}\\ & = & \frac{1}{2}\sum_{i=1}^{4}\sum_{j=1}^{4}w_{i}^{k}\,\mathbf{K}_{ij}\,w_{j}^{k}\\ & = & \frac{1}{2}\left[v_{k-1},\,(\frac{dv}{dx})_{k-1},\,v_{k},\,(\frac{dv}{dx})_{k}\right]\,\mathbf{K}^{k}\,\left[\begin{array}{c} v_{k-1}\\ (\frac{dv}{dx})_{k-1}\\ v_{k}\\ (\frac{dv}{dx})_{k} \end{array}\right] \end{eqnarray}\end{split}\]

\(\mathbf{K}_{k}\) est une matrice \((4,4)\) qui a pour expression:

\[\begin{split}\mathbf{K}^{k}=\frac{8EI_{zz}}{h^{3}}\left[\begin{array}{cccc} \int_{-1}^{+1}\left(\frac{d^{2}}{d\xi^{2}}N_{1}\right)^{2}d\xi & \frac{h}{2}\int_{-1}^{+1}\frac{d^{2}}{d\xi^{2}}N_{1}\frac{d^{2}}{d\xi^{2}}H_{1}d\xi & \int_{-1}^{+1}\frac{d^{2}}{d\xi^{2}}N_{1}\frac{d^{2}}{d\xi^{2}}N_{2}d\xi & \frac{h}{2}\int_{-1}^{+1}\frac{d^{2}}{d\xi^{2}}N_{1}\frac{d^{2}}{d\xi^{2}}H_{2}d\xi\\ \frac{h}{2}\int_{-1}^{+1}\frac{d^{2}}{d\xi^{2}}H_{1}\frac{d^{2}}{d\xi^{2}}N_{1}d\xi & \frac{h^{2}}{4}\int_{-1}^{+1}\left(\frac{d^{2}}{d\xi^{2}}H_{1}\right)^{2}d\xi & \frac{h}{2}\int_{-1}^{+1}\frac{d^{2}}{d\xi^{2}}H_{1}\frac{d^{2}}{d\xi^{2}}N_{2}d\xi & \frac{h^{2}}{4}\int_{-1}^{+1}\frac{d^{2}}{d\xi^{2}}H_{1}\frac{d^{2}}{d\xi^{2}}H_{2}d\xi\\ \int_{-1}^{+1}\frac{d^{2}}{d\xi^{2}}N_{2}\frac{d^{2}}{d\xi^{2}}N_{1}d\xi & \frac{h}{2}\int_{-1}^{+1}\frac{d^{2}}{d\xi^{2}}N_{2}\frac{d^{2}}{d\xi^{2}}H_{1}d\xi & \int_{-1}^{+1}\left(\frac{d^{2}}{d\xi^{2}}N_{2}\right)^{2}d\xi & \frac{h}{2}\int_{-1}^{+1}\frac{d^{2}}{d\xi^{2}}N_{2}\frac{d^{2}}{d\xi^{2}}H_{2}d\xi\\ \frac{h}{2}\int_{-1}^{+1}\frac{d^{2}}{d\xi^{2}}H_{2}\frac{d^{2}}{d\xi^{2}}N_{1}d\xi & \frac{h^{2}}{4}\int_{-1}^{+1}\frac{d^{2}}{d\xi^{2}}H_{2}\frac{d^{2}}{d\xi^{2}}H_{1}d\xi & \frac{h}{2}\int_{-1}^{+1}\frac{d^{2}}{d\xi^{2}}H_{2}\frac{d^{2}}{d\xi^{2}}N_{2}d\xi & \frac{h^{2}}{4}\int_{-1}^{+1}\left(\frac{d^{2}}{d\xi^{2}}H_{2}\right)^{2}d\xi \end{array}\right]\end{split}\]

C’est la matrice de raideur élémentaire. Cette matrice est symétrique, et on calcule ses coefficients en utilisant la définition des fonctions de forme (5.10). En utilisant les symétries de ces fonctions de forme, on ne calcule que 5 coefficients: \(\mathbf{K}_{11},\,\mathbf{K}_{12},\,\mathbf{K}_{13},\,\mathbf{K}_{22},\mathbf{K}_{24}\) et on déduit les autres par symétrie:

(5.12)\[\begin{split}\mathbf{K}^{k}=\frac{EI_{zz}}{h^{3}}\left[\begin{array}{cccc} 12 & 6h & -12 & 6h\\ 6h & 4h^{2} & -6h & 2h^{2}\\ -12 & -6h & 12 & -6h\\ 6h & 2h^{2} & -6h & 4h^{2} \end{array}\right]\end{split}\]

5.2.2.2. travail des forces élémentaire \(W_{k}\)

Sur un élément \(e_{k}\), le travail des forces linéiques se calcule en effectuant le passage vers l’élément de référence:

\[W_{k}=\int_{-1}^{+1}q\,\left(v_{k-1}N_{1}(\xi)+\frac{h}{2}(\frac{dv}{dx})_{k-1}H_{1}(\xi)+v_{k}N_{2}(\xi)+\frac{h}{2}(\frac{dv}{dx})_{k}H_{2}(\xi)\right)\frac{h}{2}d\xi\]

C’est une forme linéaire en fonction des valeurs nodales \(w^{k}\), qui s’écrit:

\[\begin{split}\begin{aligned} W_{k} & = & (w^{k})^{t}\mathbf{B}^{k}\\ & = & \sum_{i=1}^{4}w_{i}^{k}\,\mathbf{B}_{i}^{k}\end{aligned}\end{split}\]

\(\mathbf{B}^{k}\) est un vecteur de dimension (4), qui a pour expression:

\[\begin{split}\mathbf{B}^{k}=\frac{h}{2}\left[\begin{array}{c} \int_{-1}^{+1}qN_{1}d\xi\\ \frac{h}{2}\int_{-1}^{+1}qH_{1}d\xi\\ \int_{-1}^{+1}qN_{2}d\xi\\ \frac{h}{2}\int_{-1}^{+1}qH_{2}d\xi \end{array}\right]\end{split}\]

C’est le vecteur des forces élémentaires, qui a pour expression dans le cas d’une force linéique \(q\) constante:

(5.13)\[\begin{split}\mathbf{B}^{k}=\frac{qh}{2}\left[\begin{array}{c} 1\\ +\frac{h}{6}\\ 1\\ -\frac{h}{6} \end{array}\right]\end{split}\]

5.2.2.3. terme de bord \(W_{L}\)

le terme de bord se calcule facilement, puisque que la valeur de \(v^{h}\) en \(x=L\) vaut \(v^{h}(L)=v_{nn}\). Il vient:

\[W_{L}=Fv_{nn}\]

5.2.3. Assemblage

Le Lagrangien discret s’écrit donc:

\[\begin{split}\begin{eqnarray} \mathcal{L}(v^{h}) & = & -\frac{1}{2}\sum_{k=1}^{ne}E_{k}+\sum_{k=1}^{ne}W_{k}+W_{L}\\ & = & -\frac{1}{2}\sum_{k=1}^{ne}(w^{k})^{t}\mathbf{K}^{k}w^{k}+\sum_{k=1}^{ne}(w^{k})^{t}\mathbf{B}^{k}+Fv_{nn}\end{eqnarray}\end{split}\]

En notant \(\mathbf{X}\) le vecteur des \(2nn\) valeurs nodales inconnues:

\[\mathbf{X}^{t}=\left[\begin{array}{cccccccc} v_{1} & (\frac{dv}{dx})_{1} & v_{2} & (\frac{dv}{dx})_{1} & \ldots & \ldots & v_{nn} & (\frac{dv}{dx})_{nn}\end{array}\right]\]

ce Lagrangien s’exprime sous la forme matricielle suivante:

\[\begin{split}\begin{eqnarray} \mathcal{L}(\mathbf{X}) & = & -\frac{1}{2}\mathbf{X}^{t}\,\mathbb{A}\,\mathbf{X}+\mathbf{X}^{t}\mathbb{B}+FX_{2nn-1}\\ & = & -\frac{1}{2}\sum_{i=1}^{2nn}\sum_{j=1}^{2nn}A_{ij}X_{i}X_{j}+\sum_{i=1}^{2nn}B_{i}X_{i}+FX_{2nn-1}\end{eqnarray}\end{split}\]

\(\mathbb{A}\) est la matrice de rigidité globale du système obtenue par assemblage des matrices élémentaires \(\mathbf{K}^{k}\). Elle est symétrique et a pour dimension \((2nn,2nn)\). \(\mathbf{B}\) est le vecteur force global, obtenu par assemblage des vecteurs forces élémentaires\(\mathbf{B}^{k}\) et a pour dimension \(2nn\). Enfin le dernier terme du Lagrangien correspond à la contribution des conditions aux limites.

\(\mathcal{L}(\mathbf{X})\) est une forme quadratique symétrique par rapport aux valeurs nodales \(X_{i}\), et la condition de stationnarité de ce Lagrangien conduit aux \(2nn\) équations de Lagrange:

\[\frac{\partial L(\mathbf{X})}{\partial X_{i}}=0\]

soit

\[-\sum_{j=1}^{2nn}A_{ij}X_{j}+B_{i}+\delta_{i,2nn-1}F=0\mbox{ pour }i=1,2nn\]

C’est un système linéaire de \(2nn\) équations:

\[\mathbb{A}\,\mathbf{X}=\mathbf{B}'\,\,\mbox{ avec }\mathbf{B}'=\mathbf{B}+\left[\delta_{i,2nn-1}\right]F\]

qu’il suffit de résoudre pour obtenir la solution approchée \(v^{h}\). Ce système linéaire corresponds aussi à la formulation faible discrète de l’équation d’équilibre du système.

5.2.4. Applications

Dans le cas d’un maillage de \(\Omega\) avec \(ne=2\) éléments

\[\Omega=[0,\frac{L}{2}]\cup[\frac{L}{2},L]\]

la solution approchée possède donc au total \(2nn=4\) degrés de liberté,correspondant aux valeurs nodales aux noeuds \(x=\frac{L}{2}\) et \(x=L\), les valeurs en \(x=0\) étant imposées par les conditions aux limites.

\[v^{h}(x)=v_{1}\Phi_{1}(x)+(\frac{dv}{dx})_{1}\Psi_{1}(x)+v_{2}\Phi_{2}(x)+(\frac{dv}{dx})_{2}\Psi_{2}(x)\]

5.2.4.1. assemblage générique

De façon à effectuer l’assemblage de la matrice \(\mathbb{A}\) et du second membre \(B\) le plus simplement possible, nous allons tout d’abord considérer une solution approchée \(v^{h}\) sans tenir compte des conditions aux limites, i.e. avec \(6\)degrés de liberté:

\[v^{h}(x)=v_{0}\Phi_{0}(x)+(\frac{dv}{dx})_{0}\Psi_{0}(x)+v_{1}\Phi_{1}(x)+(\frac{dv}{dx})_{1}\Psi_{1}(x)+v_{2}\Phi_{2}(x)+(\frac{dv}{dx})_{2}\Psi_{2}(x)\]

Le vecteur inconnu \(\mathbf{X}\) s’écrit

\[\mathbf{X}=\left[\begin{array}{cccccc} v_{0} & (\frac{dv}{dx})_{0} & v_{1} & (\frac{dv}{dx})_{1} & v_{2} & (\frac{dv}{dx})_{2}\end{array}\right]^{t}\]

La matrice \(\mathbb{A}\) est l’assemblage des 2 matrices élémentaires \(\mathbf{K}^{1}\) et \(\mathbf{K}^{2}\) associées aux 2 éléments du maillage:

\[\begin{split}\mathbb{A}=\left[\begin{array}{cccccc} K_{11}^{1} & K_{12}^{1} & K_{13}^{1} & K_{14}^{1} & 0 & 0\\ K_{21}^{1} & K_{22}^{1} & K_{23}^{1} & K_{24}^{1} & 0 & 0\\ K_{31}^{1} & K_{32}^{1} & K_{33}^{1}+K_{11}^{2} & K_{34}^{1}+K_{12}^{2} & K_{13}^{2} & K_{14}^{2}\\ K_{41}^{1} & K_{42}^{1} & K_{43}^{1}+K_{21}^{2} & K_{44}^{1}+K_{22}^{2} & K_{23}^{2} & K_{24}^{2}\\ 0 & 0 & K_{31}^{2} & K_{32}^{2} & K_{33}^{2} & K_{34}^{2}\\ 0 & 0 & K_{41}^{2} & K_{42}^{2} & K_{43}^{2} & K_{44}^{2} \end{array}\right]\end{split}\]

soit en utilisant l’expression (5.12) des matrices élémentaires avec \(h=\frac{L}{2}\)

\[\begin{split}A=\frac{EI_{zz}}{L^{3}}\left[\begin{array}{cccccc} 96 & 24L & -96 & 24L & 0 & 0\\ 24L & 8L^{2} & -24L & 4L^{2} & 0 & 0\\ -96 & 24L & 192 & 0 & -96L & 24\\ 24L & 4L^{2} & 0 & 16L^{2} & -24L & 4L^{2}\\ 0 & 0 & -96 & -24L & 96 & -24L\\ 0 & 0 & 24L & 4L^{2} & -24L & 8L^{2} \end{array}\right]\end{split}\]

De même le second membre est l’assemblage des 2 seconds membres élémentaires \(\mathbf{B}^{1}\) et \(\mathbf{B}^{2}\):

\[\mathbf{B}=\left[\begin{array}{cccccc} B_{1}^{1} & B_{2}^{1} & B_{3}^{1}+B_{1}^{2} & B_{4}^{1}+B_{2}^{2} & B_{3}^{2} & B_{4}^{2}\end{array}\right]^{t}\]

ce qui donne en utilisant l’expression (5.13) du second membre élémentaire:

\[B=qL\left[\begin{array}{cccccc} \frac{1}{4} & \frac{L}{48} & \frac{1}{2} & 0 & \frac{1}{4} & \frac{L}{48}\end{array}\right]\]

5.2.4.2. conditions aux limites

Les conditions aux limites du problème sont de 2 types:

1. les conditions de Dirichlet (conditions fortes): on remplace les équations 1 et 2 par

   \[v_{0}=0\,\mbox{ et }\,(\frac{dv}{dx})_{0}=0\]

2. les conditions de Neuman (conditions faibles): on modifie le second membre pour ajouter le terme:

   \[\left[\delta_{i,2nn-1}\right]F\]

5.2.4.3. solution

Le système linéaire s’écrit alors:

\[\begin{split}\frac{EI_{zz}}{L^{3}}\left[\begin{array}{cccccc} 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0\\ -96 & 24L & 192 & 0 & -96 & 24L\\ 24L & 4L^{2} & 0 & 16L^{2} & -24L & 4L^{2}\\ 0 & 0 & -96 & -24L & 96 & -24L\\ 0 & 0 & 24L & 4L^{2} & -24L & 8L^{2} \end{array}\right]\left[\begin{array}{c} v_{1}\\ (\frac{dv}{dx})_{1}\\ v_{2}\\ (\frac{dv}{dx})_{2}\\ v_{3}\\ (\frac{dv}{dx})_{3} \end{array}\right]=qL\left[\begin{array}{c} 0\\ 0\\ \frac{1}{2}\\ 0\\ \frac{1}{4}\\ \frac{L}{48} \end{array}\right]+\left[\begin{array}{c} 0\\ 0\\ 0\\ 0\\ F\\ 0 \end{array}\right]\end{split}\]

La résolution de ce système linéaire fournit le vecteur solution approché:

\[X=[0,\,0,\,\frac{1}{384}\frac{L^{3}\left(17qL+40F\right)}{EI_{zz}},\,\frac{1}{48}\frac{L^{2}\left(7qL+18F\right)}{EI_{zz}},\,\frac{1}{24}\frac{L^{3}\left(3qL+8F\right)}{EI_{zz}},\,\frac{1}{6}\frac{L^{2}\left(qL+3F\right)}{EI_{zz}}]\]

La solution approchée s’écrit

\[\begin{split}\begin{eqnarray} v^{h}(x) & = & \frac{1}{384}\frac{L^{3}\left(17qL+40F\right)}{EI_{zz}}\Phi_{1}(x)+\frac{1}{48}\frac{L^{2}\left(7qL+18F\right)}{EI_{zz}}\Psi_{1}(x)\\ & + & \frac{1}{24}\frac{L^{3}\left(3qL+8F\right)}{EI_{zz}}\Phi_{2}(x)+\frac{1}{6}\frac{L^{2}\left(qL+3F\right)}{EI_{zz}}\Psi_{2}(x)\end{eqnarray}\end{split}\]

c’est une fonction continue à dérivée continue et qui est un polynôme de degré 3 sur chaque élément.

La solution exacte de l’équation d’équilibre (5.1) associée aux conditions aux limites (5.2),(5.3) est un polynôme de degré 4 qui s’écrit:

\[v_{ex}(x)=\frac{1}{24}\frac{qx^{4}}{EI_{zz}}-\frac{1}{6}\frac{\left(qL+F\right)x^{3}}{EI_{zz}}+\frac{1}{4}\frac{L\left(qL+2F\right)x^{2}}{EI_{zz}}\]

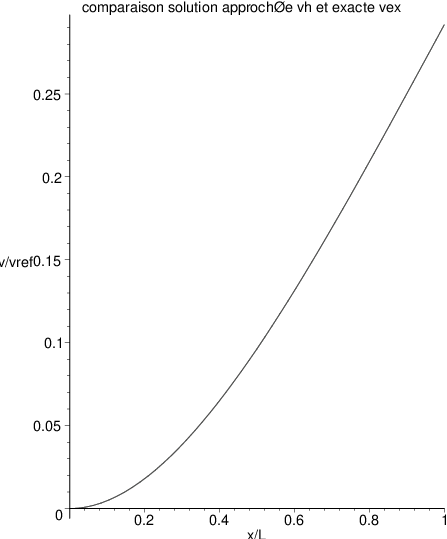
Fig. 5.4 comparaison solution exacte et approchée pour \(F=\frac{qL}{2}\) et \(v_{ref}=\frac{qL^{4}}{EI_{zz}}\)

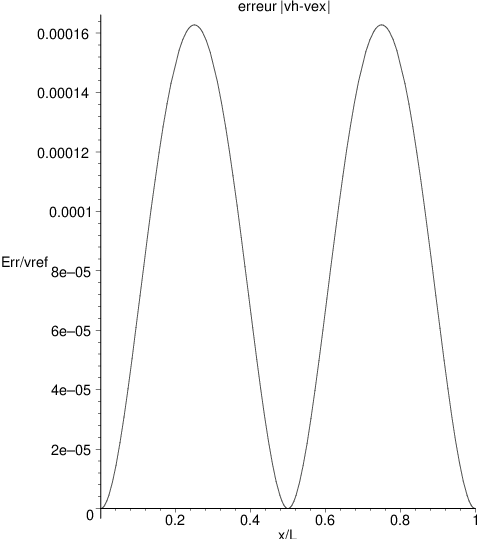
Fig. 5.5 erreur entre la solution exacte et approchée pour \(F=\frac{qL}{2}\) et \(v_{ref}=\frac{qL^{4}}{EI_{zz}}\)

On a tracé sur la figure la solution exacte \(v_{ex}\) et la solution approchée \(v^{h}\) , ainsi que la norme de l’erreur \(|v_{ex}-v^{h}|\) pour la cas \(F=\frac{qL}{2}\). On constate que dans ce cas l’approximation par éléments finis du déplacement \(v\) est excellente (les 2 courbes sont indiscernables) et on obtiens la valeur exacte aux noeuds du maillage. En particulier la méthode éléments finis prédit la déformation maximum en x=L:

\[v_{max}=\frac{L^{3}}{24EI_{zz}}(3qL+8F)\]

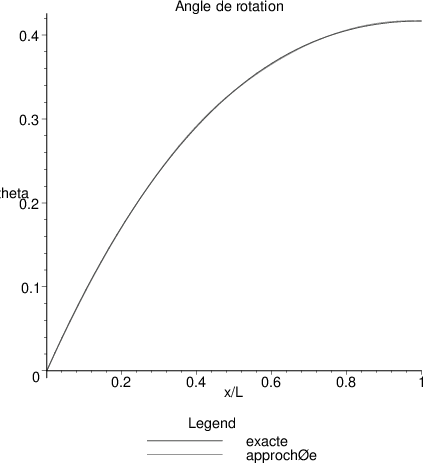
Fig. 5.6 Comparaison entre la solution exacte et la solution par éléments finis pour l’angle de rotation \(\theta\)

Fig. 5.7 Comparaison entre la solution exacte et la solution par éléments finis pour le moment fléchissant \(M_{z}\)

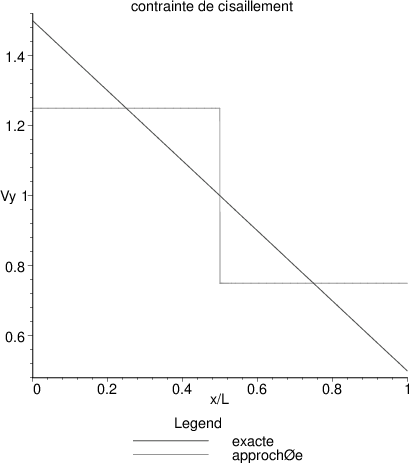
Fig. 5.8 Comparaison entre la solution exacte et la solution par éléments finis pour le cisaillement \(V_{y}\)

Sur la figure suivante, on a comparer les prédictions par éléments finis de l’angle de rotation, du moment fléchissant et de la contrainte de cisaillement avec la solution exacte. On constate une bonne prédiction de l’angle de rotation (dérivée première de \(v\)) et une assez bonne prédiction du moment fléchissant (dérivée seconde de \(v\)). Pour le cisaillement ( dérivée troisième de \(v\)), l’approximation par élément finis est constante par élément, alors que la solution exacte est linéaire. On ne prédit donc qu’une valeur moyenne par élément. On constate aussi que les conditions aux limites d’encastrement (ou conditions de Dirichlet) (5.2) sont vérifiées exactement par la solution approchée, alors que les conditions dynamiques (ou conditions de Neuman) ne sont vérifiées exactement pas:

\[EI_{zz}\frac{d^{2}v^{h}}{dx^{2}}(L)=-\frac{1}{48}qL^{2}\neq M_{z}(L)=0\,\,\,\mbox{ et }\,\,-EI_{zz}\frac{d^{3}v^{h}}{dx^{3}}(L)=F+\frac{qL}{4}\neq V_{y}=F\]

En particulier la valeur du cisaillement en \(x=L\) correspond à la valeur moyenne du cisaillement dans le dernier élément puisque:

\[\frac{2}{L}\int_{\frac{L}{2}}^{L}V_{y}dx=F+\frac{qL}{4}\,\,\mbox{ car }\,V_{y}=F+q(L-x)\]