FreeFem++ et Maillage en EF

8.3. FreeFem++ et Maillage en EF#

Marc BUFFAT, dpt mécanique, Université Claude Bernard Lyon 1

Licence Creative Commons
Mise à disposition selon les termes de la Licence Creative Commons
Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 2.0 France.

%matplotlib inline
%autosave 300
from  numpy import *
import matplotlib.pyplot as plt
from IPython.core.display import HTML

Autosaving every 300 seconds

8.3.1. Génération de maillage#

8.3.1.1. Structure de données en 2D#

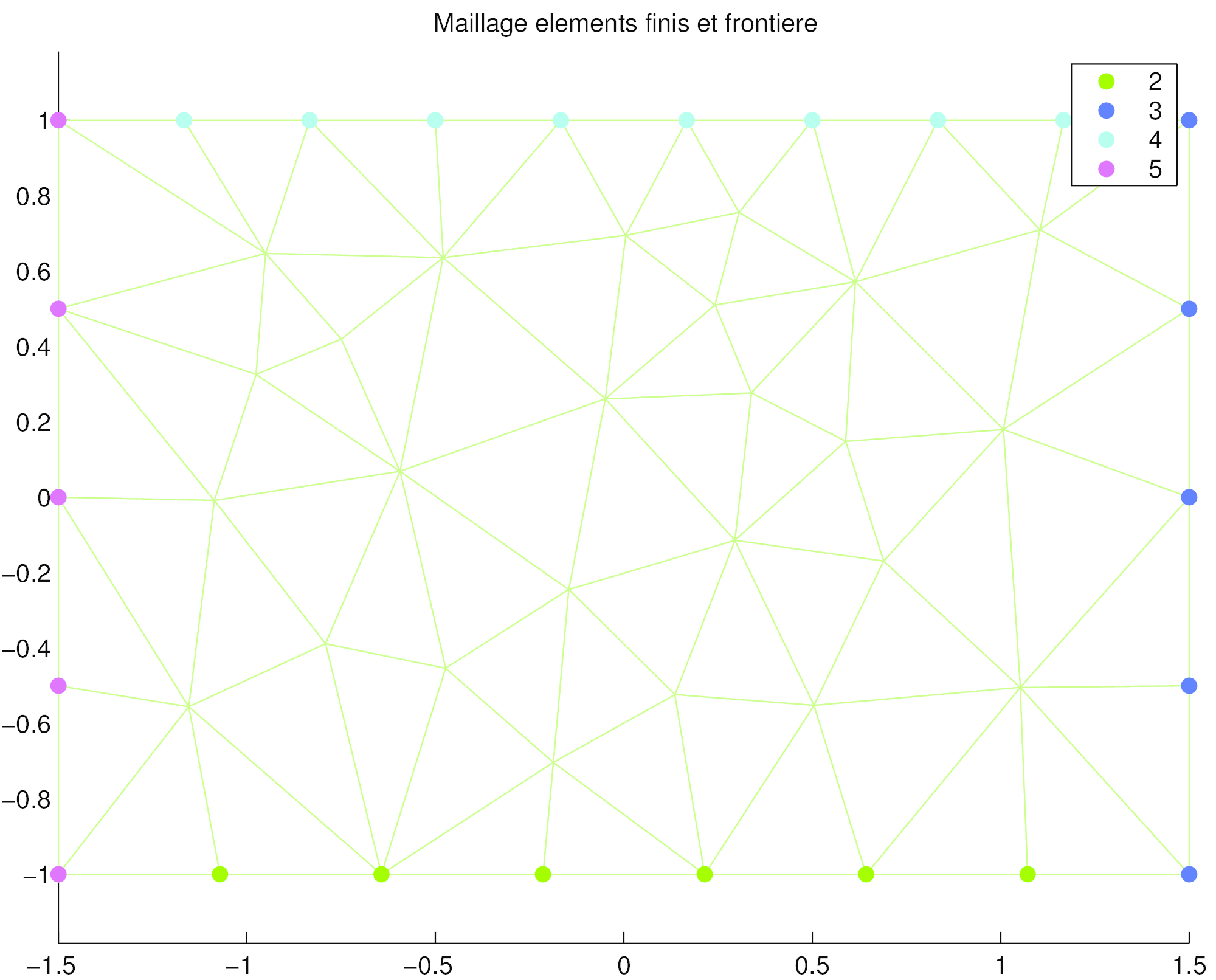
Maillage de \(ne\) triangles et \(nn\) sommets

  1. Table de connexion: tableau Tbc de nex3 entiers

  2. Coordonnées des noeuds: tableau X de nnx2 réels

  3. Frontière (noeuds): tableau frt de nn entiers

  4. Région (éléments): tableau reg de ne entiers

8.3.1.1.1. table de connexion#

<img src= »mesh1.png »; style= »width:600px »/>

8.3.1.1.2. Frontière et région#

../../../_images/mesh2.png ../../../_images/mesh3.png

8.3.1.2. Génération par transformation#

Transformation conforme vers un carre unité

../../../_images/quacou1.png ../../../_images/quacou2.png

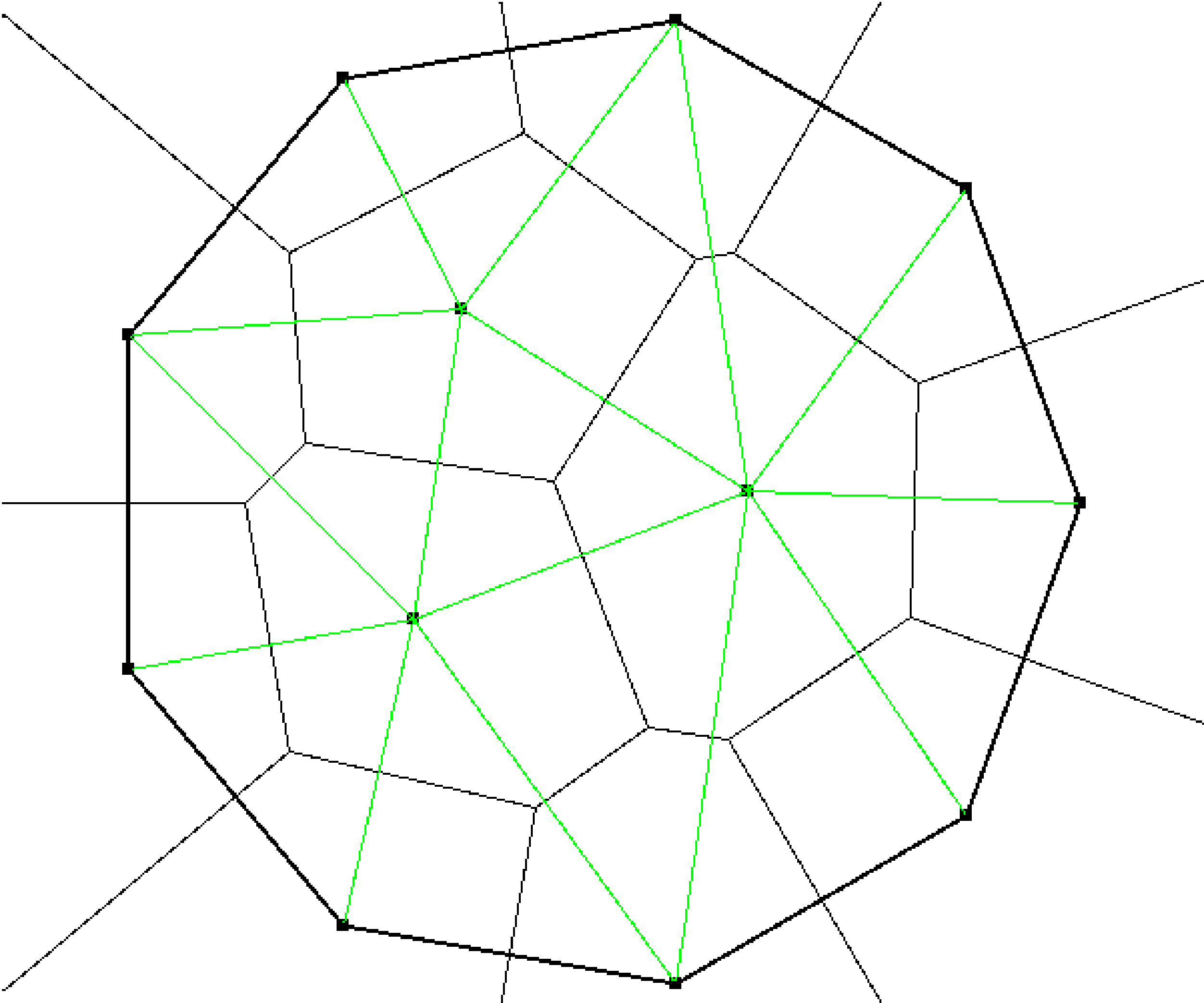
8.3.2. Voronoi#

Mailleur automatique

../../../_images/voronoi.png

8.3.3. Mailleur de FreeFem++#

(c) O. Pironneau et Frédéric Hecht Paris VI http://www.freefem.org

8.3.3.1. FreeFem++#

  • mailleur automatique Voronoi P1 (2D)

  • solveur matriciel pour des matrices de type elts finis

  • interpréteur de commande (langage de programmation)

  • création d’un fichier de commande (extension .edp)

  • execution: FreeFem++ probleme.edp

8.3.3.2. Syntaxe FreeFem++#

  • syntaxe proche du C++

  • fin instruction ;

  • structure : { .. };

  • variables: pi=3.1456;

  • résolution d’EDP

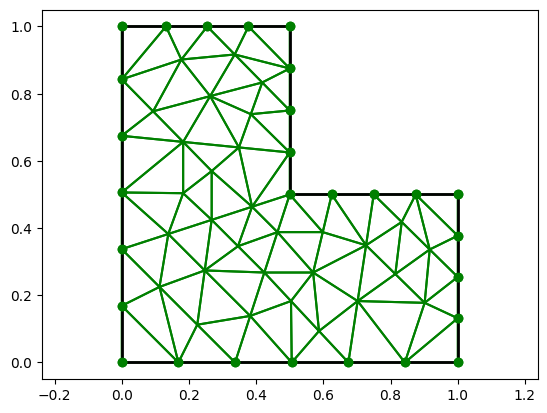
8.3.4. Mailleur Voronoi FreeFem++#

from freefem import mesh
G=mesh("essai.msh")
G.info()
G.plot()

Maillage  essai.msh
Nn,Ne= 58 86
Xmin/max Ymin/max= 0.0 1.0 0.0 1.0
surface  0.7500000000000003
../../../_images/6d3331ba51be05ee62b792736c747dfe514b8f5bf296217f60245863c9fa5f43.png

8.3.5. Syntaxe FreeFem++#

Langage proche de C++ (instruction terminée par ; , utilisation {} )

On définit un maillage \(T_h\) par la frontière \(\Gamma=\partial \Omega\) du domaine donnée par des courbes paramétrées \(\Gamma_i\):

\[ x = f_i(t) \mbox{ et } y = g_i(t) \mbox{ pour } t_1\le t \le t_2\]

8.3.5.1. description de la frontiere (sens trigonométrique)#

border nom1(t=t0,t1)
  {
    x=f1(t);
    y=g1(t);
    label=1;
  };
border nom2(t=t0,t1)
  {
    x=f2(t);
    y=g2(t);
	label=2;
  };

8.3.5.2. description des frontieres par C.L. (label)#

création et visualisation du maillage

On spécifie le nombre de points sur chaque frontière

mesh Th=buildmesh(nom1(n1)+nom2(n2));

8.3.5.3. sauvegarde du maillage dans un fichier#

savemesh(Th,'nom_fichier.msh');

8.3.6. Exemple de fichier maillage: essai.edp#

// définition des frontières
border aaa(t=0,1){x=t;y=0;label=2;};
border bbb(t=0,0.5){x=1;y=t;label=2;};
border ccc(t=0,0.5){x=1-t;y=0.5;label=2;};
border ddd(t=0.5,1){x=0.5;y=t;label=2;};
border eee(t=0.5,1){x=1-t;y=1;label=2;};
border fff(t=0,1){x=0;y=1-t;label=2;};
// generation du maillage
mesh Th = buildmesh (aaa(6) + bbb(4) + ccc(4) +ddd(4) + 
                     eee(4) + fff(6));
// sauvegarde
savemesh(Th,"essai.msh");

%%bash
FreeFem++ -nw essai.edp

-- FreeFem++ v4.9 ( - git no git)

 Load: lg_fem lg_mesh lg_mesh3 eigenvalue 

    1 : // définition des frontières

    2 : border aaa(t=0,1){x=t;y=0;label=2;};

    3 : border bbb(t=0,0.5){x=1;y=t;label=2;};

    4 : border ccc(t=0,0.5){x=1-t;y=0.5;label=2;};

    5 : border ddd(t=0.5,1){x=0.5;y=t;label=2;};

    6 : border eee(t=0.5,1){x=1-t;y=1;label=2;};

    7 : border fff(t=0,1){x=0;y=1-t;label=2;};

    8 : // generation du maillage

    9 : mesh Th = buildmesh (aaa(6) + bbb(4) + ccc(4) +ddd(4) + eee(4) + fff(6));

   10 : // sauvegarde

   11 : savemesh(Th,"essai.msh");

   12 : plot(Th);

   13 :  sizestack + 1024 =1352  ( 328 )



  --  mesh:  Nb of Triangles =     86, Nb of Vertices 58

  number of required edges : 0

times: compile 0.016655s, execution 0.007361s,  mpirank:0

 CodeAlloc : nb ptr  3707,  size :490840 mpirank: 0

Ok: Normal End

8.3.6.1. Exemple#

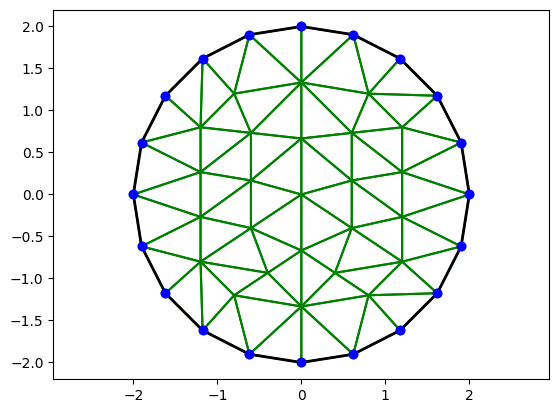
Maillage d’un cercle de rayon 1 (fichier cercle.edp)

border gamma(t=0,2*pi) 
{ x=2*cos(t); y=2*sin(t);}
Th=buildmesh(gamma(20));
savemesh(Th,"cercle.msh");

G=mesh('cercle.msh')
G.plot()
../../../_images/8fd34ff50a3489486e1c6ecda5d95d1960f5b334a915f25a4a1bcde0d7b7da9d.png

8.3.7. Solveur EF FreeFem++#

Définition du problème

\[ -\Delta u = f \mbox{ avec } u_\Gamma = 0 \]

8.3.7.1. Formulation faible#

Trouvez \(u(x,y)\) tel que \(u_\Gamma = 0\)

\[ \int_\Omega{(\frac{\partial u}{\partial x}\frac{\partial v}{\partial x} + \frac{\partial u}{\partial y}\frac{\partial v}{\partial y})} = \int_\Omega{f v\, dx dy} \ \forall v\]

8.3.7.2. Approximation avec des éléments \(P^1\)#

fespace Vh(Th,P1)
Vh u,v,f=1;

solve Lapace(u,v)= int2d(Th)(dx(u)*dx(v) + dy(u)*dy(v)) 
       - int2d(Th)(f*v) + on(Gamma,u=0); 

%%bash
FreeFem++ -nw laplace.edp

-- FreeFem++ v4.9 ( - git no git)

 Load: lg_fem lg_mesh lg_mesh3 eigenvalue 

    1 : // generation maillage cercle

    2 : {

    3 :  verbosity=2;

    4 :  border gamma(t=0,2*pi)

    5 :  { x=2*cos(t); y=2*sin(t);}

    6 :  mesh Th=buildmesh(gamma(20));

    7 :  savemesh(Th,"cercle.msh");

    8 :  plot(Th);

    9 : 

   10 :  fespace Vh(Th,P1);

   11 :  Vh u,v,f=1;

   12 : 

   13 :  solve Lapace(u,v)= int2d(Th)(dx(u)*dx(v) + dy(u)*dy(v)) 

   14 :            - int2d(Th)(f*v) + on(gamma,u=0); 

   15 :  plot(u);

   16 : }

   17 :  sizestack + 1024 =1856  ( 832 )



 Nb of common points 1

  --  mesh:  Nb of Triangles =     68, Nb of Vertices 45

    Nb of Vertices 45 ,  Nb of Triangles 68

    Nb of edge on user boundary  20 ,  Nb of edges on true boundary  20

  -- Mesh: Gibbs: old skyline = 501  new skyline = 323

  number of required edges : 0

  -- construction of the geometry from the 2d mesh 

  -- Writing the file cercle.msh of type  msh  NbOfTria = 68 NbOfRefEdge = 20

Plot bound [x,y] -2 -2 max [x,y] 2 2

  -- vector function's bound  1 1

   -- Change of Mesh 0  0x55efa9285db0

   -- size of Matrix 0 Bytes

  -- Solve : 

          min 4.04335e-31  max 0.998382

Plot bound [x,y] -2 -2 max [x,y] 2 2

times: compile 0.083123s, execution 0.153561s,  mpirank:0

 CodeAlloc : nb ptr  3656,  size :490512 mpirank: 0

Ok: Normal End

8.3.7.3. Condition aux limites sur une frontière \(\Gamma_1\)#

  • Neuman ou Fourier

\[u_{\Gamma_{1}}+\alpha(\frac{\partial u}{\partial n})_{\Gamma_{1}}=g\]
   on(Gamma1,id(u)+a*dnu(u)=g)

  • Dirichlet

\[ u_{\Gamma_2} = u_0 \]
   on(Gamma2,u=u0)

8.3.7.4. Formulation faible : intégrale#

\[\int_\Omega{() d\Omega}\]
  int2d(Th)()
\[ \int_\Gamma{ () d\Gamma}\]
  int(Gamma) ()

8.3.7.5. Liste des opérateurs#

  id(), dx(), dy(), laplace(), dxx(), dyy(), dyx(), dxy()

ATTENTION:

  dxy(u)*f = dx(f*dy(u))
  laplace(u)*(x+y)=div((x+y)*grad(u))

8.3.7.6. Tracé et sauvegarde de la solution#

  plot(Th);
  plot(u);

8.3.8. Script Freefem#

8.3.8.1. Structure de données#

La géométrie éléments finis est stockée dans un fichier texte (avec une extension .msh) avec la structure de données suivante (format FreeFEM). Ce fichier contient les informations suivantes par ligne:

  1. \(n_{s}\,\,\,\, n_{t}, \, nn_f \)

  2. \(x_{1}\,\,\, y_{1}\,\,\,\,{nf}_{1}\)

  3. …..

  4. \(x_{i}\,\,\, y_{i}\,\,\,\,{nf}_{i}\)

  5. …..

  6. \(x_{n_{s}}\,\,\,\, y_{n_{s}}\,\,\,\,{nf}_{n_{s}}\)

  7. \(tbc_{1,1}\,\,\, tbc_{1,2}\,\,\,\,\, tbc_{1,3}\,\,\,\,\, e_{1}\)

  8. ……

  9. \(tbc_{k,1}\,\,\, tbc_{k,2}\,\,\,\,\, tbc_{k,3}\,\,\,\,\, e_{k}\)

  10. ……

  11. \(tbc_{n_{t},1}\,\,\, tbc_{n_{t},2}\,\,\,\,\, tbc_{n_{t},3}\,\,\,\,\, e_{n_{t}}\)

où \(n_{s}\) est le nombre de sommets (noeuds) du maillage, \(n_{t}\) le nombre d’éléments et \(nn_f\) le nombre de noeuds sur la frontière. Pour chaque noeud \(i\) on donne les coordonnées \((x_{i},y_{i})\) ainsi que le numéro de la frontière ou se trouve le noeud \((nf_{i})\) (0 si le noeud est interne). Pour chaque élément \(k\), on a le numéro des 3 sommets \((tbc_{k,1}\,\,\, tbc_{k,2}\,\,\,\,\, tbc_{k,3})\) ainsi que le numéro de région \(e_{k}\).

Le fichier a donc \(1+n_{s}+n_{t}\) lignes.

8.3.8.2. maillage à partir de script généré sous Python#

from freefem import meshFreefem
# SCRIPT FREEFEM++
script="""
border aaa(t=0,1){x=t;y=0;label=2;};
border bbb(t=0,0.5){x=1;y=t;label=2;};
border ccc(t=0,0.5){x=1-t;y=0.5;label=2;};
border ddd(t=0.5,1){x=0.5;y=t;label=2;};
border eee(t=0.5,1){x=1-t;y=1;label=2;};
border fff(t=0,1){x=0;y=1-t;label=2;};
mesh Th = buildmesh (aaa(6) + bbb(4) + ccc(4) +ddd(4) + eee(4) + fff(6));
savemesh(Th,\"essai1.msh\");
"""
G=meshFreefem("essai1",script)
G.plot()

-- FreeFem++ v4.9 ( - git no git)
 Load: lg_fem lg_mesh lg_mesh3 eigenvalue 
    1 : 
    2 : border aaa(t=0,1){x=t;y=0;label=2;};
    3 : border bbb(t=0,0.5){x=1;y=t;label=2;};
    4 : border ccc(t=0,0.5){x=1-t;y=0.5;label=2;};
    5 : border ddd(t=0.5,1){x=0.5;y=t;label=2;};
    6 : border eee(t=0.5,1){x=1-t;y=1;label=2;};
    7 : border fff(t=0,1){x=0;y=1-t;label=2;};
    8 : mesh Th = buildmesh (aaa(6) + bbb(4) + ccc(4) +ddd(4) + eee(4) + fff(6));
    9 : savemesh(Th,"essai1.msh");
   10 :  sizestack + 1024 =1352  ( 328 )

  --  mesh:  Nb of Triangles =     86, Nb of Vertices 58
  number of required edges : 0
times: compile 0.015369s, execution 0.009033s,  mpirank:0

 CodeAlloc : nb ptr  3705,  size :490400 mpirank: 0
Ok: Normal End
../../../_images/6d3331ba51be05ee62b792736c747dfe514b8f5bf296217f60245863c9fa5f43.png 
script="""
border aa(t=0,2*pi) { x=2*cos(t); y=2*sin(t); label=1; };
border bb(t=0,2) {
if(t<=1) { 
    x= t-0.5; 
    y= 0.17735*sqrt(t)-0.075597*t-0.212836*(t^2)+0.17363*(t^3)-0.06254*(t^4);\
} else {
    x= 2-t-0.5;
    y= -(0.17735*sqrt(2-t)-0.075597*(2-t)-0.212836*((2-t)^2)+0.17363*((2-t)^3) - 0.06254*(2-t)^4);\
}; 
label=2; }
mesh Th=buildmesh(aa(40)+bb(41));
savemesh(Th,"naca.msh");
"""
G=meshFreefem("naca",script)
plt.figure(figsize=(14,8))
G.plot(front=False)

-- FreeFem++ v4.9 ( - git no git)
 Load: lg_fem lg_mesh lg_mesh3 eigenvalue 
    1 : 
    2 : border aa(t=0,2*pi) { x=2*cos(t); y=2*sin(t); label=1; };
    3 : border bb(t=0,2) {
    4 : if(t<=1) { 
    5 :     x= t-0.5; 
    6 :     y= 0.17735*sqrt(t)-0.075597*t-0.212836*(t^2)+0.17363*(t^3)-0.06254*(t^4);} else {
    7 :     x= 2-t-0.5;
    8 :     y= -(0.17735*sqrt(2-t)-0.075597*(2-t)-0.212836*((2-t)^2)+0.17363*((2-t)^3) - 0.06254*(2-t)^4);}; 
    9 : label=2; }
   10 : mesh Th=buildmesh(aa(40)+bb(41));
   11 : savemesh(Th,"naca.msh");
   12 :  sizestack + 1024 =1288  ( 264 )

  --  mesh:  Nb of Triangles =   1099, Nb of Vertices 590
  number of required edges : 0
times: compile 0.01279s, execution 0.06644s,  mpirank:0
 CodeAlloc : nb ptr  3685,  size :487584 mpirank: 0
Ok: Normal End
../../../_images/b83c358a051b3cb1cb362368b4cc612994dc37ef967727522a5b12f86fba4293.png 
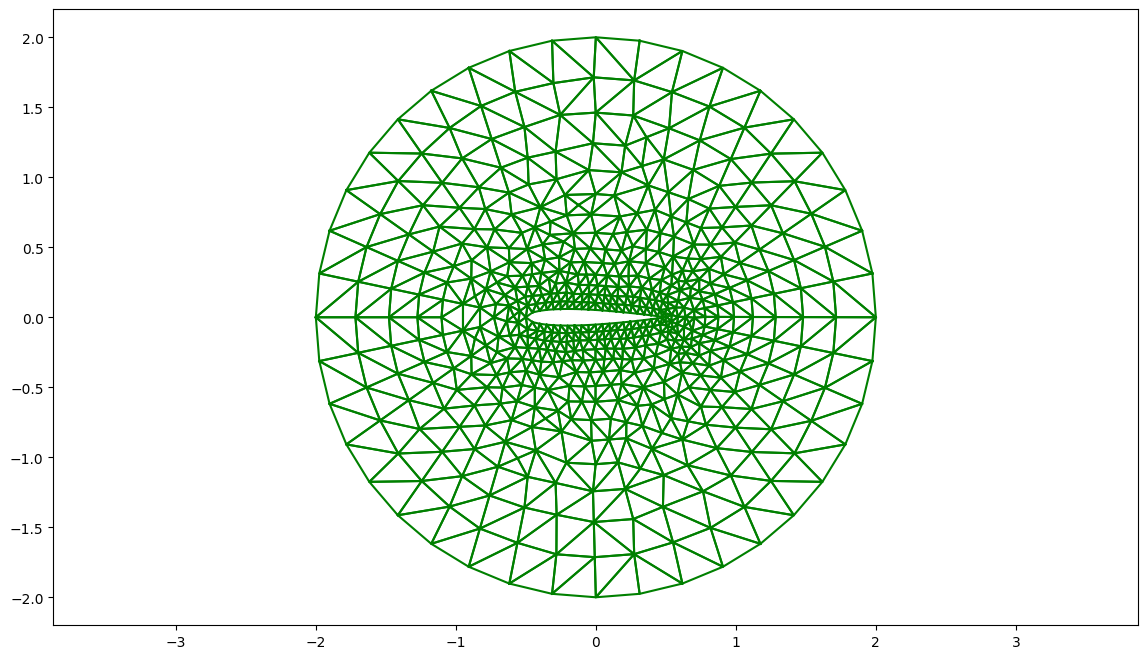
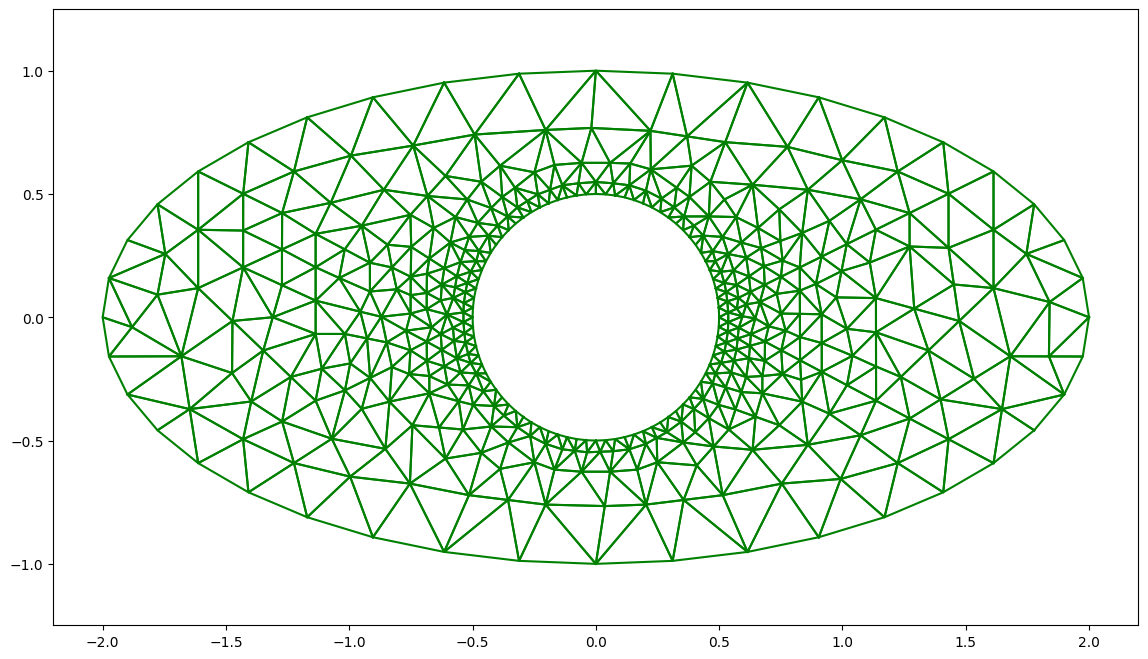
script="""
real a=2.,b=1.; 
border Gamma(t=0,2*pi)  { x = a * cos(t);   y = b*sin(t); label=1; }
border Gamma2(t=0,2*pi) { x = 0.5 * cos(t); y = 0.5*sin(-t); label=2; }
// maillage
mesh Th=buildmesh(Gamma(40)+Gamma2(80));
savemesh(Th,"ellipse2.msh");
"""
G=meshFreefem("ellipse2",script)
plt.figure(figsize=(14,8))
G.plot(front=False)

-- FreeFem++ v4.9 ( - git no git)
 Load: lg_fem lg_mesh lg_mesh3 eigenvalue 
    1 : 
    2 : real a=2.,b=1.; 
    3 : border Gamma(t=0,2*pi)  { x = a * cos(t);   y = b*sin(t); label=1; }
    4 : border Gamma2(t=0,2*pi) { x = 0.5 * cos(t); y = 0.5*sin(-t); label=2; }
    5 : // maillage
    6 : mesh Th=buildmesh(Gamma(40)+Gamma2(80));
    7 : savemesh(Th,"ellipse2.msh");
    8 :  sizestack + 1024 =1304  ( 280 )

  --  mesh:  Nb of Triangles =    762, Nb of Vertices 441
  number of required edges : 0
times: compile 0.012498s, execution 0.052331s,  mpirank:0
 CodeAlloc : nb ptr  3619,  size :486112 mpirank: 0
Ok: Normal End
../../../_images/e569d393c72f3f807345089834f8ba731d70bafb8df16c0238ae37b836cdae81.png

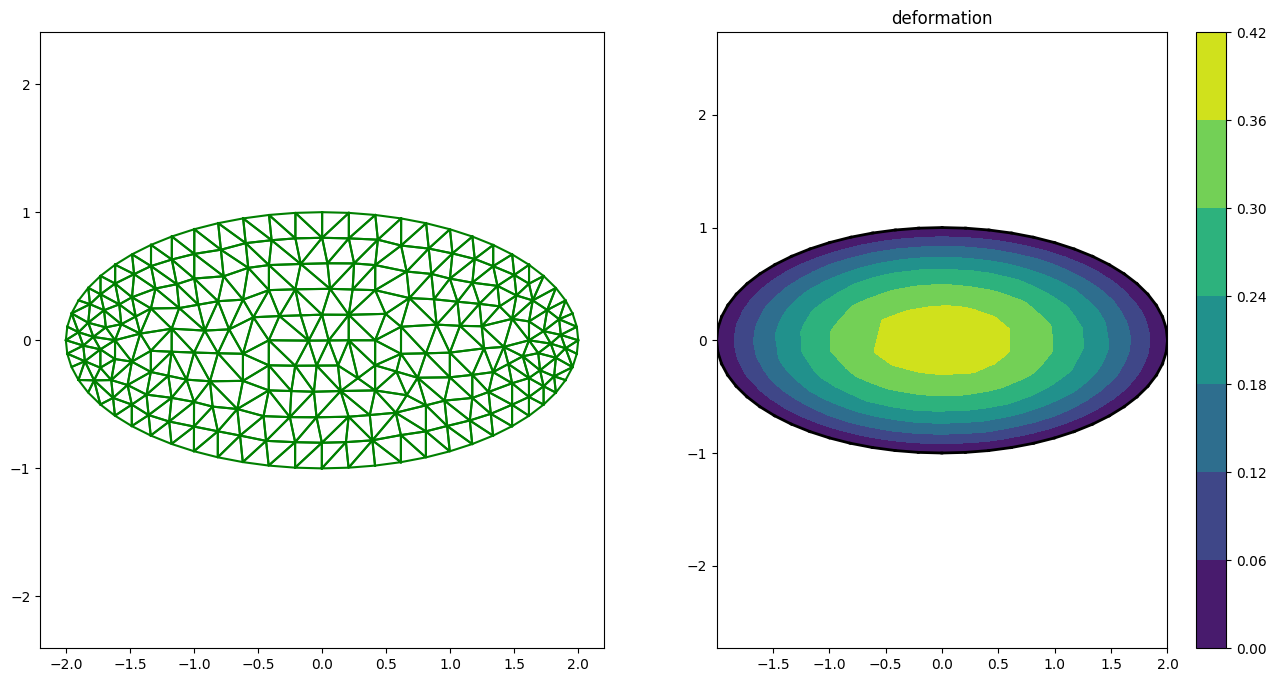
8.3.9. Exemple: déformation d’une membrane#

from freefem import Freefem,readres
# execution script FreeFem avec lecture du resultat
script="""
real theta=4.*pi/3.;real a=2.,b=1.; func Z=0.;
border Gamma1(t=0,theta)    { x = a * cos(t); y = b*sin(t); label=1; }
border Gamma2(t=theta,2*pi) { x = a * cos(t); y = b*sin(t); label=2; }
// maillage
mesh Th=buildmesh(Gamma1(40)+Gamma2(20));
savemesh(Th,"membrane.msh");
// solveur
fespace Vh(Th,P1);
Vh phi,w, f=1;
solve Laplace(phi,w)=int2d(Th)(dx(phi)*dx(w) + dy(phi)*dy(w)) - int2d(Th)(f*w) + on(Gamma2,phi=0) + on(Gamma1,phi=Z);
// ecriture resultat
{ ofstream ff("membrane.res"); 
  ff<<phi[].n<<endl; 
  for(int i=0; i<phi[].n;i++) ff<<phi[][i]<<endl; 
}
"""

Freefem("membrane",script,True)
G=mesh("membrane.msh")
G.info()
U=readres("membrane.res")
plt.figure(figsize=(16,8))
plt.subplot(1,2,1)
G.plot(False)
plt.subplot(1,2,2)
plt.axis('equal')
G.isosurf(U,"deformation")

Maillage  membrane.msh
Nn,Ne= 235 408
Xmin/max Ymin/max= -1.99999929654 2.0 -0.999999665197 0.9999999163
surface  6.27170743614086
lecture resultat  235 235
../../../_images/02095507b8790ad83ba83162e74ebac481c02068de01cafdd6534fd850361084.png

8.3.10. FIN#

Contenu