8. Problème instationnaire (hyperbolique)#
8.1. Etude de la vibration d’une corde souple#
Considérons une corde tendue suivant l’axe \(Ox\), initialement au repos avec une longueur \(L\) et soumise à une tension \(T_{0}\)[1], que l’on déforme à l’instant \(t=0\). C’est le problème de la corde pincée d’un instrument de musique (clavecin), dont on se propose d’étudier la vibration (figure Fig. 8.1).
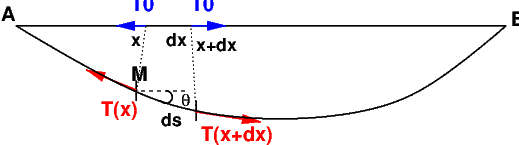
Fig. 8.1 corde tendue souple au repos et à un instant t#
On suppose que la corde est sans raideur (ou souple), c’est à dire que la résultante des contraintes est la tension \(T(x)\) qui reste tangente à la corde. On néglige en particulier le moment de flexion qui apparaît si la corde possède une raideur (cas d’une poutre). On tiens cependant compte de l’élasticité de la corde, qui peut s’allonger proportionnellement à une variation de tension.
Considérons un élément de corde \(MM'\) de longueur \(ds\) (figure Fig. 8.1) situé en un point \(M\) de la corde. Au repos ce brin de corde \(MM'(0)\) est situé au point \(M(x,0)\) d’abscisse \(x\), d’ordonnée \(y=0\) et a pour longueur \(dx\) : \(M'=M'(x+dx,0)\)
A l’instant \(t\) il a subit un déplacement longitudinal \(u(x,t)\) et un déplacement transversal \(y(x,t)\). Le point \(M\) se trouve donc en \(x+u\) et \(y\): \(M=M(x+u,y)\) et le point \(M'\) en \(x+u+du\) et \(y+dy\): \(M'=M'(x+dx+u+du,y+dy)\). Le brin \(MM'\) fait un angle \(\theta(x,t)\) avec l’axe \(Ox\) et sa longueur \(ds\) vaut donc \(ds^{2}=(dx+du)^{2}+dy^{2}\), soit puisque les variables ne dépendent que de \(x\) et du temps \(t\):
L’angle \(\theta\) vérifie les relations suivantes:
Pour de petits déplacements (\(du\ll dx,\,\,dy\ll dx)\), et à un instant \(t\) fixé on en déduit les relations suivantes:
L’allongement relatif du brin \(MM'\) s’écrit:
La tension dans la corde est donc la somme de la tension initiale \(T_{0}\) et d’une contrainte élastique, qui d’après la théorie de l’élasticité linéaire s’écrit:
où \(E\) est le module d’Young de la corde et \(S\) sa section.
L’équation d’équilibre dynamique pour le brin \(MM'\) de masse volumique \(\rho\):
En ne conservant que les termes du premier ordre (petites oscillations), on obtiens un système de 2 équations découplées :
qui sont 2 équations des ondes, correspondant respectivement à des ondes de flexion ( \(y(x,t)\)) de célérité \(c_{y}=\sqrt{\frac{T_{0}}{\rho S}}\) et des ondes de compression (\(u(x,t)\)) de célérité \(c_{u}=\sqrt{\frac{ES}{\rho S}}\).
Dans la cas d’une corde de section \(S\) constante, ces 2 équations s’écrivent sous la forme d’une équation des ondes avec une célérité constante \(c_{0}\) (\(c_{0}=c_{y}\) ou \(c_{0}=c_{u}\)):
Dans le cas d’une corde de section \(S(x)\) non constante (de section moyenne \(S_{0}\)), cette équation s’écrit:
avec \(\alpha=\frac{S}{S_{0}}\), \(\beta=1\) et \(c_{0}=\sqrt{\frac{T_{0}}{\rho S_{0}}}\) pour l’onde de flexion \(y(x,t)\) et \(\alpha=\frac{S}{S_{0}}\), \(\beta=\alpha\) et \(c_{0}=\sqrt{\frac{ES_{0}}{\rho S_{0}}}\) pour l’onde de compression \(u(x,t)\).
A cette équation on ajoutte des conditions aux limites de déplacement nul aux 2 extrémitées:
et des conditions initiales (CI) : déformation \(v_{0}(x)\) sans vitesse initiale
8.2. Formulation faible#
La formulation faible de l’équation des ondes (8.3) s’obtient classiquement en multipliant par une fonction test \(w(x)=\delta v\) (variation de \(v(x,t)\) à un instant t fixé), et en intégrant l’équation à \(t\) fixé sur le domaine de calcul:
En intégrant par partie le membre de droite, et en utilisant les conditions aux limites de Dirichlet (CL) sur \(v\) (8.5), qui imposent des conditions homogènes sur la variation \(w\)
on obtiens la formulation faible suivante:
Cette formulation faible correspond au théorème des travaux virtuels, qui traduit la condition de minimisation de l’action \(\mathcal{A}=\int_{0}^{\tau}\mathcal{L}(v,\dot{v})\,dt\), avec un Lagrangien:
La formulation variationnelle associée s’écrit alors:
8.3. Formulation éléments finis#
Pour construire une approximation \(v^{h}\) par éléments finis de la solution de (8.6), on utilise un maillage \(\mathcal{M}^{h}\) du domaine de calcul \(\Omega=[0,L]\) en \(ne\) éléments \(\left\{e_{k}=[x_{k-1},x_{k}]\right\}_{k=1,ne}\) associé à \(ne+1\) noeuds \(\left\{ x_{i}\right\} _{i=0,ne}\). On choisit ensuite une interpolation en espace de la solution. Pour notre étude nous utiliserons des éléments finis \(\mathcal{P}^{1}\). La solution approchée s’écrit alors comme une combinaison linéaire des fonctions de base \(\left\{ \Phi_{i}(x)\right\}\)associées à ce maillage \(\mathcal{M}^{h}\) et à l’interpolation \(\mathcal{P}^{1}\):
En tenant compte des conditions aux limites (8.5), et des propriétés des fonctions de base \(\Phi_{i}(x_{j})=\delta_{ij}\):
l’approximation possède \(ne-1\) degrés de liberté et s’écrit:
On note que, contrairement aux problèmes statiques étudiés précédemment, les coefficients \(v_{i}\) de la combinaison linéaire (valeurs nodales) dépendent maintenant du temps. Les fonctions tests \(w^{h}(x)\) étant des variations (à \(t\) fixé) de la solution \(v^{h}\), c.a.d. une combinaison des fonctions de base, on choisit comme fonctions tests les fonctions de base \(\Phi_{i}\). La formulation faible discrète s’écrit alors:
C’est un système de \(ne-1\) équations différentielles linéaires du second ordre qui s’écrit sous la forme matricielle:
où \(\mathbf{M}\) est la matrice de masse, \(\mathbf{K}\) la matrice de rigidité et \(V\) le vecteur inconnu des valeurs nodales:
Ce système s’écrit sous la forme suivante (noté le signe - devant la matrice \(\mathbf{A}\)):
auquel on ajoute les conditions initiales (8.6). La matrice \(\mathbf{A}\) est une matrice symétrique et définie positive[2], puisque \(\mathbf{M}\) et \(\mathbf{K}\) sont des matrices symétriques définies positives. \(\mathbf{A}\)possède donc \(ne-1\) valeurs propres réelles positives, que l’on note \(\omega_{i}^{2}\).
La solution générale de ce système d’équations différentielles linéaires est donc la somme de \(ne-1\) solutions élémentaires où modes propres \(\Lambda_{i}\) :
les \(\Lambda_{i}\) étant les vecteurs propres associés aux valeurs propres \(\omega_{i}^{2}\) de la matrice \(\mathbf{A}\):
D’un point de vue mécanique, la vibration du système est une combinaison de modes propres de vibration \(\Lambda_{i}\) associés à des fréquences propres \(\frac{2\pi}{\omega_{i}}\). On obtiens ainsi les premiers modes de vibrations de la corde.
8.4. Assemblage et calcul des modes propres#
Le calcul des matrices de masse et de raideur utilise la technique d’assemblage décrite dans les chapitres précédents.
On calcule tout d’abord une matrice de masse et de raideur élémentaire sur l’élément de référence, ce qui permet d’obtenir les matrices élémentaires de masse \(\mathbf{M}^{k}\) et de raideur \(\mathbf{K}^{k}\) sur un élément \(e_{k}\) de longueur \(h\):
On effectue ensuite un assemblage élément par élément pour calculer les matrices globales de raideur \(\mathbf{K}\) et de masse \(\mathbf{M}\), puis on applique les conditions aux limites.
La prise en compte des conditions aux limites est effectuée en éliminant les lignes et les colonnes des 2 noeuds frontières (noeud 1 et noeud N).
Pour calculer les valeurs propres et vecteurs propres de la matrice \(\mathbf{A}=\mathbf{M}^{-1}\mathbf{K}\), on résout le problème équivalent de valeurs propres généralisés:
en utilisant une fonction de calcul de valeurs propres en spécifiant que les matrices sont symétriques définie positives.
8.5. Résultats#
Le calcul a été fait avec \(Ne=10\) éléments, soit \(9\) degrés de liberté. Le nombre de modes propres calculés est donc \(9\).
L’amplitude des modes propres de vibration calculés est tracé sur les figures ci-dessous pour les modes \(k=1\) \(k=6\) et \(k=8\) et comparé à la solution analytique \(\sin k\pi x\).
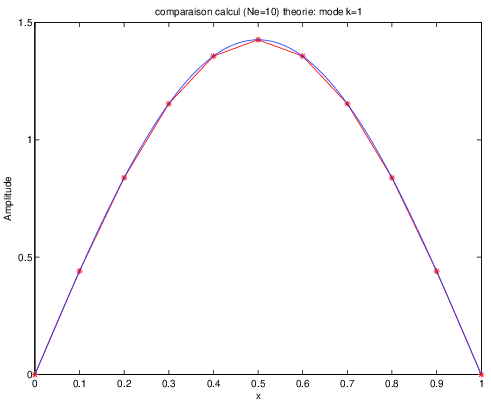
Fig. 8.2 mode 1#
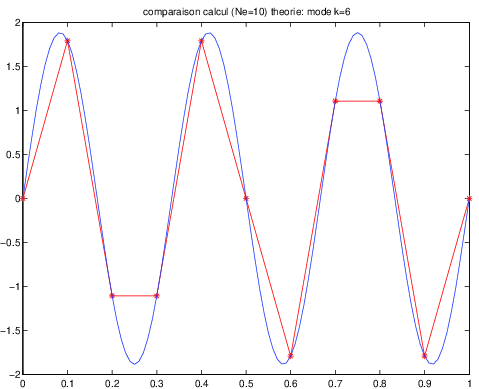
Fig. 8.3 mode 6#
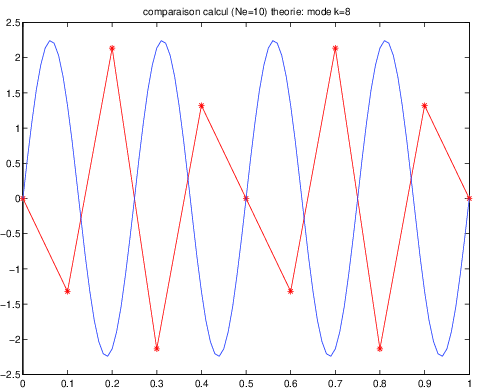
Fig. 8.4 mode 8#
On constate que la précision diminue lorsque \(k\) augmente.
De même, on a tracé la courbe des fréquences propres calculés comparées aux fréquences analytiques \(k/2\)
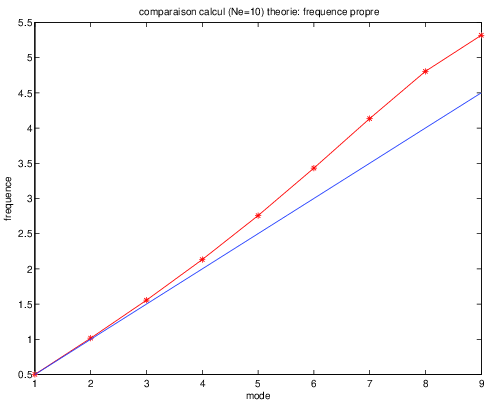
Fig. 8.5 fréquences propres#
On constate la encore une diminution importante de la précision lorsque \(k\) augmente.
Conclusion: on vérifie le théorème de Shanon sur l’échantillonnage !
