8.2. Résolution équation de Laplace par éléments Finis#
Marc BUFFAT, dpt mécanique, Université Claude Bernard Lyon 1
Mise à disposition selon les termes de la Licence Creative Commons
Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 2.0 France.
%matplotlib inline
%autosave 300
from numpy import *
import matplotlib.pyplot as plt
from IPython.core.display import HTML
Autosaving every 300 seconds
8.2.1. Mise en équation#
8.2.1.1. Equation d’équilibre#
8.2.1.2. Formulation variationnelle#
Trouver \(u\) avec \(u_\Gamma=0\) t.q.
8.2.2. Approximation Elements finis#
maillage de \(\Omega\)
approximation sur maillage \(u_h\)
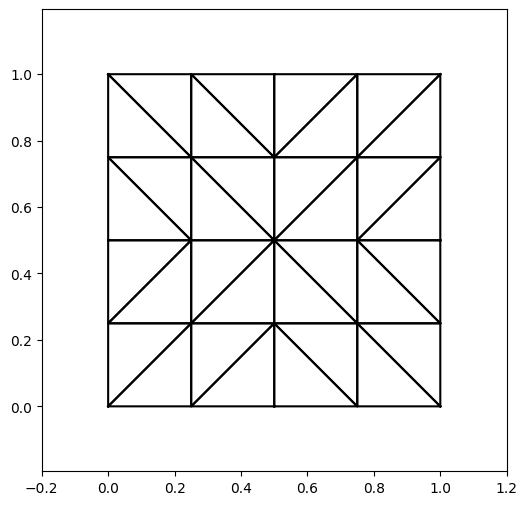
8.2.2.1. Maillage éléments finis#
triangulation de \(\Omega\) en \(Ne\) éléments : \( \Omega = \sum_{k=1}^{Ne} e_k \)
from Maillage import Maillage
# maillage carre unité
G=Maillage(nom="maillage grossier")
G.quadrangle([[0.,0.],[1.,0.],[1.,1.],[0.,1.]],3,3,num=[2,2,2,2],ttype=2)
G=G.raffine() # raffinement
G.info()
# tracer
plt.figure(figsize=(6,6))
plt.axis('equal')
plt.axis([-0.2,1.2,-0.2,1.2])
G.plotmesh()
plt.draw()
maillage grossier x2
ne= 32 nn= 25 type= 1 ddl= 3
Xmin/max Ymin/max= 0.0 1.0 0.0 1.0
Surface 1.0
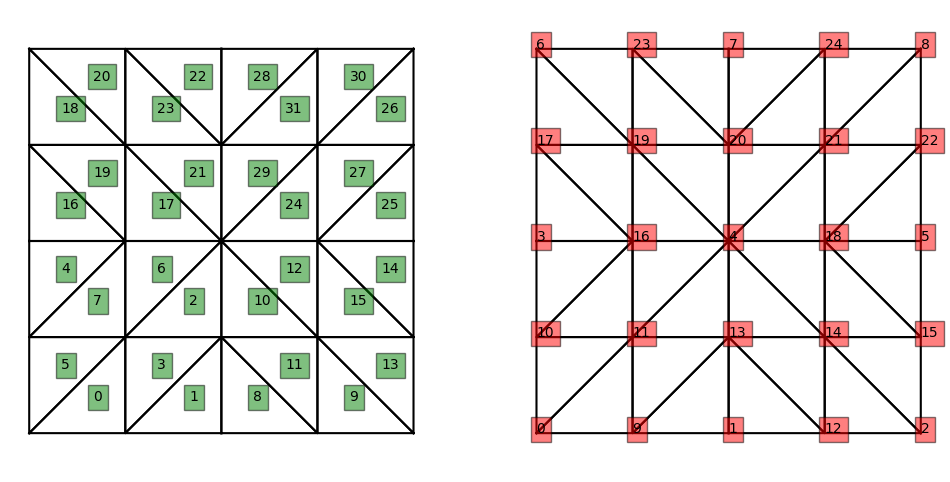
8.2.2.2. structure de données#
numérotation des \(Ne\) éléments
numérotation des \(Nn\) sommets (noeuds)
Un maillage éléments finis est donc constitué des informations suivantes:
le nombre de noeuds nn, le nombre d’éléments ne,
les coordonnées \((x_{i},y_{i})\) de chaque noeud \(M_{i}\) du maillage,
les numéros des sommets de chaque élément \(e_{k}\) (ou table de connection): \(tbc_{k,1},\, tbc_{k,2}\,,tbc_{k,3}\)
pour chaque noeud \(M_{i}\) , une information (i.e. un entier) \(frt_{i}\) qui précise si le noeud est interne (\(frt_{i}=0\)), ou sur une frontière \(\Gamma_{l}\) (\(frt_{i}=l\))
pour chaque élément \(e_{k}\), une information de région \(reg_{k}\), indiquant le numéro du domaine auquel appartiens l’élément. Par défaut il n’y a qu’un seul domaine et \(reg_{k}=1\) pour tous les éléments.
plt.figure(figsize=(12,6))
plt.subplot(1,2,1)
G.plotmesh()
G.plotelt()
plt.axis('equal')
plt.axis('off')
plt.subplot(1,2,2)
G.plotmesh()
G.plotnds()
plt.axis('equal')
plt.axis('off')
plt.show()
POur représenter ces données on utilise une structure de données Maillage (de classe sous Python) avec (en notant G le nom de variable Maillage):
G.nn nbre de noeuds de la géométrie G : entier
G.ne nbre d’éléments de la géométrie G : entier
G.ddl nbre de degré de liberté par éléments (=3 pour des éléments \(\mathcal{P}^{1}\) en 2D) : entier
G.X tableau des coordonnées (x,y) des noeuds: tableau G.nn*G.dim réels
G.Tbc table de connection: tableau G.ne*G.ddl entiers
G.Frt numéro de frontière par noeuds: tableau G.nn entiers
G.Reg numéro de région par éléments: tableau G.ne entiers
print("Maillage ",G.nn,G.ne,G.ddl)
print("Table de connection")
print(G.Tbc[:5,:])
print("Coordonnées des noeuds")
print(G.X[:4,:])
Maillage 25 32 3
Table de connection
[[ 0 9 11]
[ 1 13 9]
[ 4 11 13]
[13 11 9]
[ 3 10 16]]
Coordonnées des noeuds
[[0. 0. ]
[0.5 0. ]
[1. 0. ]
[0. 0.5]]
8.2.2.3. Frontière et Conditions aux limites#
plt.figure(figsize=(5,5))
G.plotfront()
plt.axis('equal')
plt.axis([-0.2,1.2,-0.2,1.2])
plt.show()
print("Code pour les noeuds frontières ")
print(G.Frt)
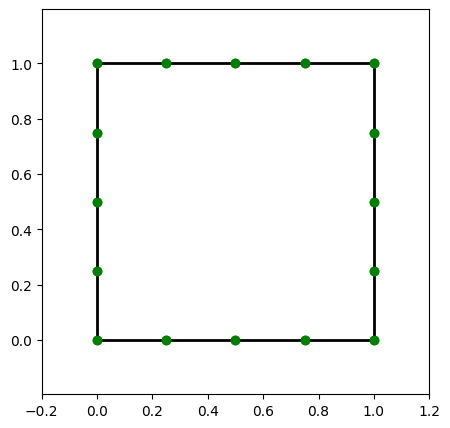
Code pour les noeuds frontières
[2 2 2 2 0 2 2 2 2 2 2 0 2 0 0 2 0 2 0 0 0 0 2 2 2]
8.2.3. Approximation élèments finis \(P^1\)#
8.2.3.1. Fonction de base \(\Phi_i(x,y)\)#
Les fonctions \(\Phi_{i}\) forment une base locale, i.e. une fonction \(\Phi_{i}(x,y)\) est non nulle uniquement sur une petite partie du maillage: le support du noeud \(M_{i}\), i.e. l’ensemble des éléments \(e_{l}\) ayant le noeud \(M_{i}\) comme sommet (\(M_{i}\in e_{l}\)).
Elles vérifient les propriétés suivantes:
la fonction de base \(\Phi_{i}(x,y)\) vaut 1 au noeud i et 0 sur tous les autres noeuds: \(\Phi_{i}(x_{j},y_{j})=\delta_{ij}\)
la fonction de base \(\Phi_{i}(x,y)\) est non nulle uniquement sur son support \(Sup_{i}=\{\cup e_{k}\,/M_{i}\in e_{k}\}\) $\(N_{i}(x,y)\neq0\,{\, si\,}\,(x,y)\in Sup_{i}\)$
la fonction de base \(\Phi_{i}(x,y)\) est orthogonale à presque toutes les autres fonctions de base \(\Phi_{j}\), en particulier celles qui sont associées à des noeuds j non voisin de i (t.q. \(Sup_{i}\cap Sup_{j}=\emptyset\)) : $\( \Phi_{i}(x,y)*\Phi_{j}(x,y)\,\left\{ \begin{array}{cc} =0 & \mbox{ si }\,Sup_{i}\cap Sup_{j}=\emptyset\\ =0 & \mbox{ si }\,(x,y)\notin(Sup_{i}\cap Sup_{j})\\ \neq0 & \mbox{ si }\,(x,y)\in(Sup_{i}\cap Sup_{j}) \end{array}\right. \)$
8.2.3.2. Fonctions de base sur un élément \(e_k\)#
Sur un élément \(e_k\), il n’y a que 3 fonctions de base non nulles associées aux 3 sommets \([n_1,n_2,n_3]\)
Ces 3 fonctions de base peuvent s’exprimer en fonction des coordonnées barycentriques \({\lambda_i}\) sur l’élement \(e_k\):
8.2.3.2.1. coordonnées barycentriques#
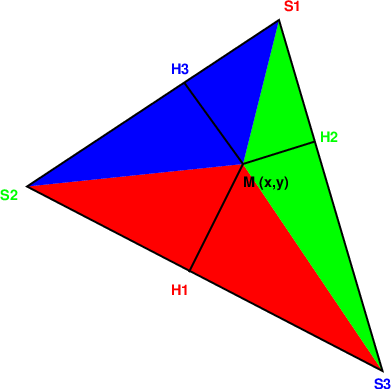
Ces coordonnées sont définies de la façon suivante: pour chaque point \(M\) de coordonnées \((x,y)\), le vecteur \(\overrightarrow{OM}\) s’écrit en fonction des sommets du triangle, comme combinaison des vecteurs \(\overrightarrow{OS_{1}}\), \(\overrightarrow{OS_{2}}\), \(\overrightarrow{OS_{3}}\). Les coefficients sont les coordonnées barycentriques par rapport au triangle considéré, i.e.
Les valeurs de \(\lambda_{1},\lambda_{2},\lambda_{3}\) vérifient les relations (voir la figure pour les notations):
qui donnent les expressions suivantes:
8.2.3.3. approximation EF#
solution approchée $\(u^h(x,y) = \sum_{j=1}^{Nn} u_j \Phi_j(x,y) \)$
fonctions test $\(v^h(x,y) = \Phi_i(x,y)\)$
interpolation 2nd membre
8.2.3.4. formulation faible discrete#
8.2.3.5. système matricielle#
avec \(K\) matrice de rigidité et \(M\) matrice de masse $\(K_{ij}=\int_\Omega{\nabla \Phi_j \nabla \Phi_i \, d\omega}\)\( \)\(M_{ij}=\int_\Omega{\Phi_j \Phi_i \, d\omega}\)$
Le calcul des matrices \(K\) et \(M\) se fait élément par élément
8.2.4. Calcul des matrices élémentaires#
8.2.4.1. Matrice élémentaire de rigidité#
Nous rappelons de la matrice de rigidité calculée sur un élément \(e_k\) de sommet \([n_1,n_2]\) est une matrice 3x3:
Les propriétés de symétrie de cette matrice montrent qu’elle ne dépend que de 3 coefficients, que l’on peut écrire sous forme vectorielle: $\( \mathbf{K}_{22}^{k}=\frac{\left\Vert \overrightarrow{S_{1}S_{3}}\right\Vert ^{2}}{4aire_{k}},\,\mathbf{K}_{33}^{k}=\frac{\left\Vert \overrightarrow{S_{2}S_{1}}\right\Vert ^{2}}{4aire_{k}},\,\mathbf{K}_{23}^{k}=\frac{\overrightarrow{S_{1}S_{3}}.\overrightarrow{S_{2}S_{1}}}{4aire_{k}}, \)\( avec \)\( aire_{k}=\frac{1}{2}\left\Vert \overrightarrow{S_{1}S_{3}}\otimes\overrightarrow{S_{2}S_{1}}\right\Vert \)\( que l'on reporte dans l'expression de \)\mathbf{K}^{k}$
En utilisant les notations matricielles, ces formulent se programment très simplement. La fonction MatRigidite implémente les relations précédentes en utilisant une méthode gradient qui calcule pour un élément k le gradient \(\nabla \lambda_p\) des 3 fonctions de base dans un tableau 2x3 \(dN\) ainsi que l’aire du triangle. On a aussi utiliser le fait que le produit vectoriel \(\overrightarrow{S_{1}S_{3}}\otimes\overrightarrow{S_{2}S_{1}}\) a une seule composante non nulle, qui est suivant l’axe z, et qui est positive si les sommets sont donnés dans l’ordre trigonométrique dans la table de connexion (ce qui est le cas).
8.2.4.2. Matrice élémentaire de masse#
La matrice élémentaire de masse s’écrit:
Le calcul donne l’expression de la matrice de masse élémentaire:
qui est implémenté dans la fonction MatMasse .
def MatRigidite(G,k):
""" calcul matrice de rigidite sur l'elt k du maillage G """
dN,Aire=G.gradient(k)
K22=dot(dN[:,1],dN[:,1])*Aire
K33=dot(dN[:,2],dN[:,2])*Aire
K23=dot(dN[:,1],dN[:,2])*Aire
Ke=array([[K22+K33+2*K23, -K23-K22,-K23-K33],
[-K23-K22 , K22 , K23],
[-K23-K33 , K23 , K33]])
return Ke
def MatMasse(G,k):
""" calcul matrice de masse sur l'elt k du maillage G """
Aire=G.aire(k)
Me=Aire/12.0*array([[ 2, 1 ,1 ],
[ 1, 2 ,1 ],
[ 1, 1 ,2 ]])
return Me
8.2.5. Assemblage#
L’assemblage de la matrice \(\mathbf{K}\) et du second membre \(\mathbf{B}\) consiste à passer en revu les éléments, à calculer les matrices élémentaires de masse et de rigidité, puis à mettre ses valeurs aux bons endroits dans la matrice et le second membre globale.
L’algorithme d’assemblage ci dessous donne le principe de cette assemblage.
K=0, M=0 #initialisation
pour k de 1 à ne # boucle sur les éléments
calcul des matrices Ke et Me
ni = Tbc[k,:] # numéros des noeuds de l'élément
pour p de 1 à 3
np = n[p]
pour q de 1 à 3
nq = n[q]
K[np,nq] = K[np,nq] + Ke[p,q]
M[np,nq] = M[np,nq] + Me[p,q]
fin q
fin p
fin k
Le programme Assemblage implémente cet algorithme, en utilisant les notations matricielles avec adressage indirecte qui permettent d’éviter l’écriture de boucles.
def Assemblage(G):
K=zeros((G.nn,G.nn))
for k in range(G.ne):
Ke=MatRigidite(G,k)
ni=G.Tbc[k,:]
K[ix_(ni,ni)] += Ke
return K
def Smb(G,F):
B=zeros((G.nn))
for k in range(G.ne):
Me=MatMasse(G,k)
ni=G.Tbc[k,:]
Fe=F[ix_(ni)]
B[ix_(ni)] += dot(Me,Fe)
return B
8.2.5.1. calcul de l’intégale \(L^2\) d’une fonction f#
et sur un élément \(k\)
def intL2(G,F):
""" calcul integrale L2 d'une fonction F sur un maillage G """
somme=0.0
for k in range(G.ne):
Me = MatMasse(G,k)
ni = G.Tbc[k,:]
Fe = F[ix_(ni)]
somme += dot(Fe,dot(Me, Fe))
return somme
8.2.6. Résolution#
L’application des conditions aux limites sur le système linéaire \(\mathbf{A} U = \mathbf{B}\) obtenu après l’assemblage dépend du type de conditions aux limites.
L’imposition des conditions aux limites de Dirichlet consiste à fixer la valeur de la solution aux noeuds \(M_{i}\) se trouvant sur la frontière de Dirichlet. Pour cela on remplace simplement dans le système linéaire l’équation \(i\) par la condition aux limites \(u_i = 0\).
Dans la matrice \(\mathbf{A}\), cela revient à annuler la ligne \(i\) et à mettre un 1 sur la diagonale, et dans le second membre \(\mathbf{B}\), à remplacer la composante i par 0 $\( \mathbf{A}_{ij}=0,\,\mathbf{A}_{ii}=1,\,\mathbf{B}_{i}=0\,\)$
Après imposition des conditions aux limites, la solution approchée \(u^{h}\) s’obtiens par résolution du système linéaire qui fournit les valeurs nodales \(U\) de \(u^h\).
# resolution EF
print("Resolution Laplacien maillage grossier")
F=ones(G.nn)
A=Assemblage(G)
B=Smb(G,F)
# conditions limites
for i in range(G.nn):
if G.Frt[i]==2:
A[i,:]=0.; A[:,i]=0.; A[i,i]=1.0;
B[i]=0.0
# resolution
U=linalg.solve(A,B)
print("solution min/max=",amin(U),amax(U))
G.isosurf(U,"Solution EF")
plt.axis('equal'); plt.axis('off')
Resolution Laplacien maillage grossier
solution min/max= 0.0 0.078125
(0.0, 1.0, 0.0, 1.0)
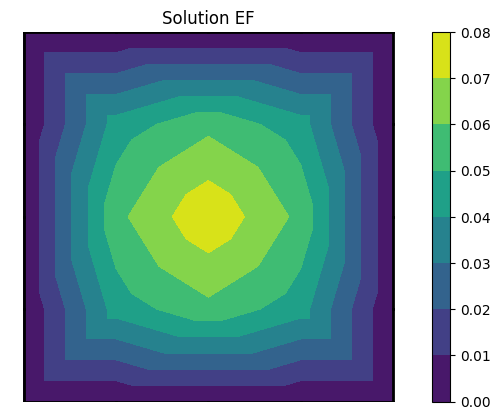
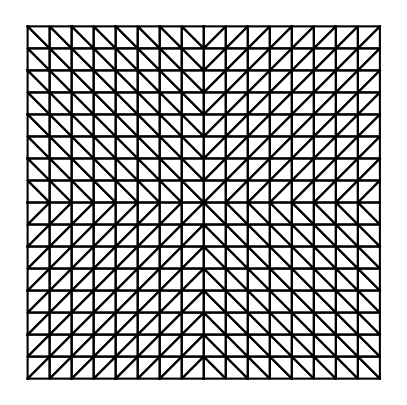
8.2.7. Résolution sur un maillage raffinée x4#
G2=G.raffine()
G2=G2.raffine()
G2.info()
plt.figure(figsize=(5,5))
plt.axis([-0.2,1.2,-0.2,1.2])
plt.axis('equal'); plt.axis('off')
G2.plotmesh()
plt.draw()
# calcul 2nd membre
F2=ones(G2.nn)
maillage grossier x2 x2 x2
ne= 512 nn= 289 type= 1 ddl= 3
Xmin/max Ymin/max= 0.0 1.0 0.0 1.0
Surface 1.0
print("Resolution Laplacien maillage raffine")
A=Assemblage(G2)
B=Smb(G2,F2)
# conditions limites
for i in range(G2.nn):
if G2.Frt[i]==2:
A[i,:]=0.; A[:,i]=0.; A[i,i]=1.0;
B[i]=0.0
# resolution
U2=linalg.solve(A,B)
print("solution min/max=",amin(U2),amax(U2))
G2.isosurf(U2,"Solution EF")
plt.axis('equal'); plt.axis('off')
Resolution Laplacien maillage raffine
solution min/max= 0.0 0.07422713801727826
(0.0, 1.0, 0.0, 1.0)
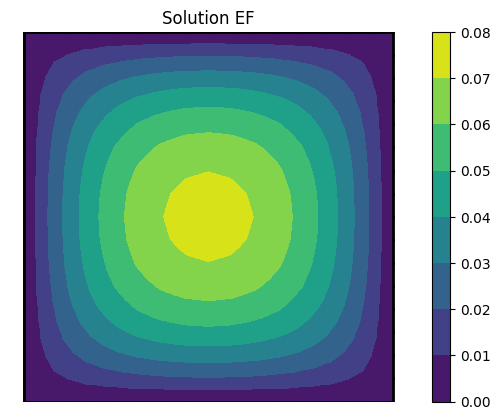
8.2.8. Validation#
solution analytique pour \(f=2\pi^2 \sin{\pi x} \sin{\pi y} \)
8.2.8.1. mode propre#
8.2.8.2. Calcul de l’erreur sur le maillage grossier#
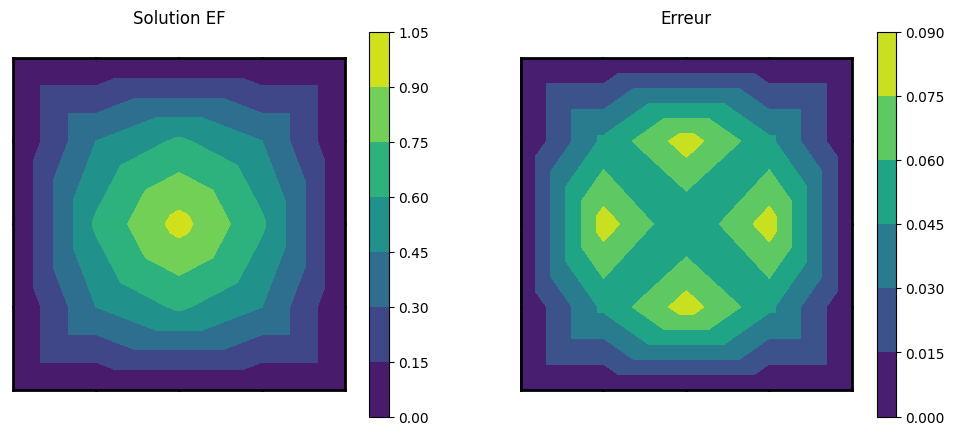
def trace(G,U,Uex):
""" tracer solution EF et solution exacte """
plt.figure(figsize=(12,5))
plt.subplot(1,2,1)
plt.axis('equal'); plt.axis('off')
G.isosurf(U,"Solution EF")
plt.axis([-0.01,1.01,-0.01,1.01])
plt.subplot(1,2,2)
plt.axis('equal'); plt.axis('off')
G.isosurf(Uex-U,"Erreur")
plt.axis([-0.01,1.01,-0.01,1.01])
plt.show()
return
uex=lambda x,y : sin(pi*x)*sin(pi*y)
Uex=G.interp(uex)
f=lambda x,y : 2*pi**2*sin(pi*x)*sin(pi*y)
F=G.interp(f)
print("Resolution Laplacien maillage grossier")
A=Assemblage(G)
B=Smb(G,F)
# conditions limites
for i in range(G.nn):
if G.Frt[i]==2:
A[i,:]=0.; A[:,i]=0.; A[i,i]=1.0;
B[i]=0.0
# resolution
U=linalg.solve(A,B)
print("erreur min/max L2=",amin(Uex-U),amax(Uex-U),sqrt(intL2(G,Uex-U)))
trace(G,U,Uex)
Resolution Laplacien maillage grossier
erreur min/max L2= 0.0 0.08219354053971506 0.042440171218571285
8.2.8.3. Calcul de l’erreur sur le maillage fin x4#
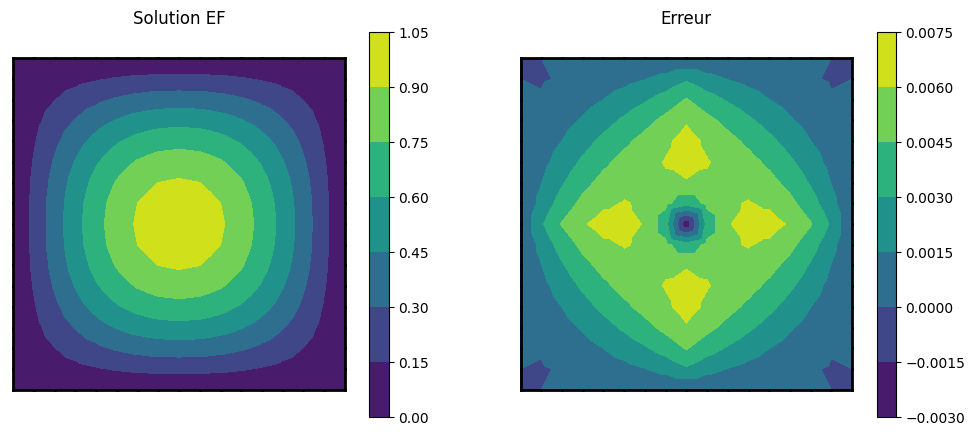
G2 maillage raffinée x4, donc avec une taille \(h/4\)
Erreur \(\theta(h^2)\) donc divisée par 16.
U2ex=G2.interp(uex)
F2=G2.interp(f)
print("Resolution Laplacien maillage fin")
A=Assemblage(G2)
B=Smb(G2,F2)
# conditions limites
for i in range(G2.nn):
if G2.Frt[i]==2:
A[i,:]=0.; A[:,i]=0.; A[i,i]=1.0; B[i]=0.0
# resolution
U2=linalg.solve(A,B)
print("erreur min/max, L2=",amin(U2ex-U2),amax(U2ex-U2),sqrt(intL2(G2,U2ex-U2)))
# tracer
trace(G2,U2,U2ex)
Resolution Laplacien maillage fin
erreur min/max, L2= -0.002565190312218135 0.006640675633780679 0.0035540352120353312
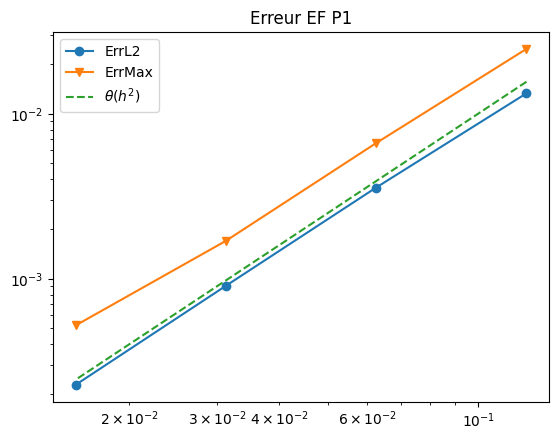
8.2.9. Evolution de l’erreur#
On veut vérifier que l’erreur d’approximation par éléments finis \(P^1\) varie en \(O(h^2)\) en calculant l’erreur pour une serie de maillages de plus en plus raffinés.
def calculErr(G,nfois):
""" calcul erreur sur un maillage raffiné nfois """
# maillage
G2=G.raffine()
for k in range(nfois-1):
G2=G2.raffine()
# calcul solution
U2ex = G2.interp(uex)
F2 = G2.interp(f)
A=Assemblage(G2)
B=Smb(G2,F2)
# conditions limites
for i in range(G2.nn):
if G2.Frt[i]==2:
A[i,:]=0.; A[:,i]=0.; A[i,i]=1.0;
B[i]=0.0
# resolution
U2=linalg.solve(A,B)
Err2=abs(U2ex-U2)
ErrMax=amax(Err2)
ErrL2=sqrt(intL2(G2,Err2))
print("solution EF min/max=",amin(U2),amax(U2))
print("erreur min/max=",ErrMax)
print("norme L2 erreur =",ErrL2)
return ErrMax,ErrL2
h0=1./4. # h maillage initial
N=4 # nbre de raffinement
H = array([h0/2**(n+1) for n in range(N)])
ErrL2=zeros(N)
ErrMax=zeros(N)
for n in range(N):
print("niveau de raffinement ",n+1)
ErrMax[n],ErrL2[n]=calculErr(G,n+1)
niveau de raffinement 1
solution EF min/max= 0.0 0.998536781992073
erreur min/max= 0.024715726580774033
norme L2 erreur = 0.013294528911815267
niveau de raffinement 2
solution EF min/max= 0.0 1.0025651903122181
erreur min/max= 0.006640675633780679
norme L2 erreur = 0.0035698437451023384
niveau de raffinement 3
solution EF min/max= 0.0 1.0013674968117194
erreur min/max= 0.00169600290706029
norme L2 erreur = 0.0009056742260279603
niveau de raffinement 4
solution EF min/max= 0.0 1.0005208361339273
erreur min/max= 0.0005208361339272827
norme L2 erreur = 0.0002272878038711298
plt.loglog(H,ErrL2,'-o',label="ErrL2")
plt.loglog(H,ErrMax,'-v',label="ErrMax")
plt.loglog(H,H*H,'--',label="$\\theta(h^2)$")
plt.title("Erreur EF P1")
plt.legend(loc=0)
<matplotlib.legend.Legend at 0x7f3aa3d8b850>
