Introduction

Contenu

1. Introduction#

Ce cours est la seconde version de mon cours d’éléments finis en master mécanique. La première version, qui se trouve ici

Méthode des éléments finis en Mécanique: approche illustrée avec Maple et Matlab

utilisait des exemples de programmes sous Maple et Matlab. Cette nouvelle version est une mise à jour importante, avec maintenant des exemples de programme écrit en Python et l’utilisation de notebook Ipython.

1.1. Objectifs#

En mécanique, la modélisation de nombreux problèmes conduit à des équations aux dérivées partielles, dont on ne connaît pas en général de solutions analytiques. La puissance des ordinateurs et des logiciels permet aujourd’hui de calculer des solutions numériques de la plupart de ces équations aux dérivées partielles.

L’objectif du cours est de comprendre les principes de la méthode des éléments finis, qui est une des méthodes numériques les plus utilisées en mécanique et d’acquérir une démarche de modélisation numérique rigoureuse. En effet, même s’il existe des logiciels de modélisation par éléments finis très sophistiqués, il est important de comprendre les méthodes numériques utilisées, pour pouvoir utiliser ces logiciels intelligemment en connaissant leurs limites et surtout pouvoir valider la simulation en ayant une idée des erreurs d’approximation.

Le cours se base sur une approche mécanicienne, dans laquelle on explique les principes sans forcement faire de démonstrations rigoureuses au sens mathématique. En particulier on n’utilisera très peu d’analyse fonctionnelle, ni d’espaces de Hilbert, qui sont la base des théories mathématiques sur les éléments finis, utiliser en particulier pour démontrer existence et unicité des solutions approchées. Néanmoins, le cours nécessite un certain nombre de connaissances préalables:

en mécanique analytique: principe des travaux virtuels
en analyse mathématique: intégration, dérivation de fonction
en analyse numérique: interpolation, approximation d’intégrale

1.1.1. compétences à acquérir#

connaître le principe de la méthode des éléments finis
savoir formuler un problème d’EDP (équations aux dérivées partielles) sous forme de formulation faible (Lagrange)
savoir construire une approximation
connaître les propriétés de l’approximation ( précision/propriétés )
savoir mettre en oeuvre cette méthode sur des cas simples: i.e. la programmer en Python pour comprendre
savoir utiliser intelligemment des logiciels d’EF (COMSOL)

1.2. Historique#

1.2.1. ère pré-informatique (début 20ième)#

Les mathématiciens se sont intéressés très tôt à la recherche de solutions approchées, bien avant l’avènement des ordinateurs. La théorie mathématique d’approximation des EDP est basée sur le calcul variationnel, l’approximation et l’interpolation développés en particulier par:

Lord Rayleigh(Anglais 1842-1919) , Walter Ritz (Suisse 1878-1909), Boris Galerkin (Russe 1871-1945)
Richard Courant (Allemand 1888-1972)

1.2.2. début de l’ère informatique (1960-1970)#

écriture des premiers programmes de calcul par EF en mécanique des structures

Zinkiewicz (Swansea), Argiris (Stuttgart), Ciarlet (Paris VI), ..
la NASA sponsorise les premières versions de NASTRAN

Une formulation mathématique rigoureuse est présentée dans le livre de Strang et Fix (1973), et les mathématiciens de l’école française d’analyse numérique (Cialet, Raviard).

1.2.3. développement et généralisation#

approximation d’EDP dans tous les domaines des sciences
- électromagnétisme, thermique, mécanique des fluides
approche multi-physique (COMSOL, ..)
extensions de la méthode des E.F.
- h-méthode,
- p-methode,
- discontinuous Galerkin

1.3. Exemples de simulations par EF#

1.3.1. Vibration d’un vilebrequin#

Maillage (à gauche), champ de contrainte et de déplacement (à droite)

vibtaion d'un vilbrequin

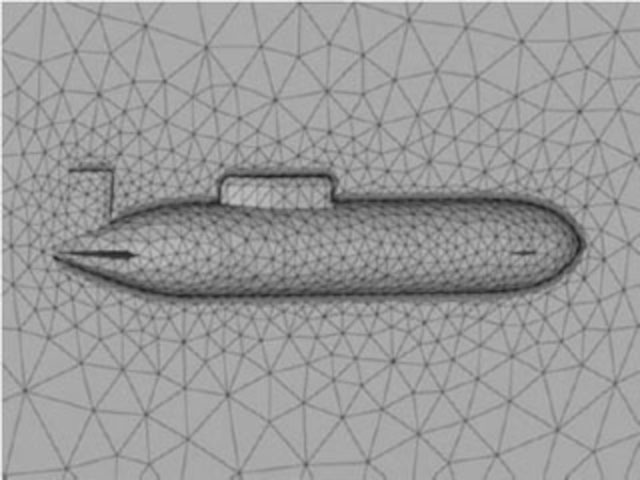
1.3.2. Écoulement autour d’un sous-marin#

Maillage de la coque d’un sous marin pour le calcul de l’écoulement

sousmarin

1.3.3. CFD (Computational Fluid Dynamics?)#

Mais attention au mirage des images issues de la simulation. Ce n’est pas parce que le résultat est joli, que le calcul a un sens, comme ici avec l’écoulement autour du vaisseau l’entreprise.

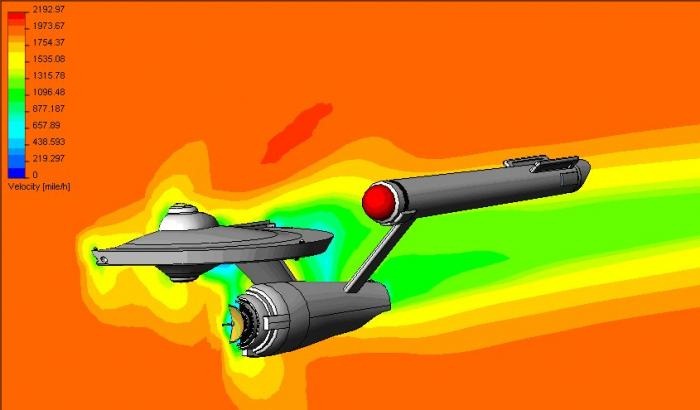
startrek

Il ne faut pas transformer la CFD (Computational Fluid Dynamics) en Color Fluid Dynamics.

1.4. Concept de base#

La méthode des éléments finis est une technique numérique permettant de résoudre des équations différentielles partielles (EDP) en approximant la solution sur un domaine discretisé en éléments. Elle est largement utilisée en ingénierie pour traiter des problèmes de mécanique des solides, thermique, fluide, électromagnétisme, etc.

Le principe de la méthode des éléments finis est de calculer une approximation $u^h$ de la solution $u_e$ d’une EDP dans un domaine $\Omega$

Pour cela la démarche utilisée est la suivante

démarche de simulation

discrétisation du domaine par un maillage
choix du type d’interpolation (polynomiale) sur chaque élément de ce maillage: fonctions de forme $N_i(x)$ et des inconnues valeurs nodales $u_i$
en déduire la forme de l”approximation globale $$u^h = \sum u_i N_i(x)$$
sur chaque élément, écrire les équations élémentaires reliant les inconnues sur l’élément: matrice élémentaire $K^e$ et second membre élémentaire $f^e$
en déduire le système d’équations globales par assemblage pour obtenir la matrice globale $K$ et le second membre global $f$
application des conditions aux limites
résolution pour calculer les valeurs nodales et déterminer la solution $u^h$
estimation d’erreur $|u_e-u^h|$
adaptation du maillage pour améliorer la solution si nécessaire

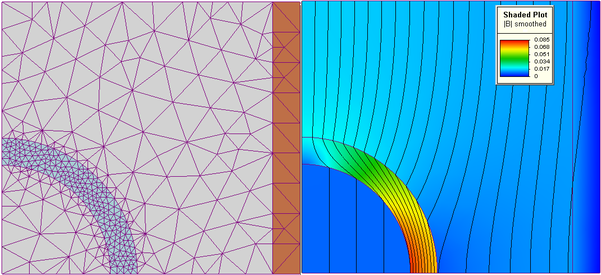
1.4.1. Exemple: solution d’un problème elliptique (calcul de champ scalaire)#

Exemple de base d’un maillage et de la solution, où l’on remarque l’utilisation d’un maillage non uniforme avec un raffinement de la solution

maillage

1.4.2. Principes de base#

Le principe de base repose sur une idée classique en science:

« Remplacer un problème complexe par une somme de problèmes simples »

Pour cela on va mettre en oeuvre les étapes suivantes:

Étape	Action	Objectif
1. Maillage	Diviser le domaine ($\omega$) en un ensemble d’éléments simples (triangles, quadrilatères, tétraèdres, etc.).	Réduire le problème continu à une structure discrète.
2. Fonctions de forme	Choisir des fonctions locales $N_i(x)$ (généralement polynomiales) qui interpolent la solution à l’intérieur d’un élément.	Relier les valeurs aux nœuds aux valeurs continues dans l’élément.
3. Approximation globale	Représenter la solution comme combinaison linéaire des fonctions de forme pondérées par les inconnues nodales : $u_h(x)=\sum_{i} N_i(x) u_i$.	Convertir le problème différentiel en système d’équations algébriques.
4. Équations élémentaires	Substituer l’approximation dans l’équation différentielle et effectuer l’intégration sur chaque élément.	Obtenir la matrice d’élément $K^{e}$ et le vecteur de force $f^{e}$.
5. Assemblage	Assembler les matrices et vecteurs locaux en une matrice globale ($K$) et un vecteur global ($f$).	Respecter la continuité entre les éléments et tenir compte de toutes les contraintes.
6. Conditions aux limites	Imposer les contraintes (déplacements fixes, flux, etc.) sur le périmètre.	Modifier le système global (remplir, supprimer, ou ajuster des lignes/colonnes).
7. Résolution	Résoudre le système linéaire $KU = f$ (ou itératif pour les non linéaires).	Obtenir les valeurs nodales $U=\{u_i\}$ qui approximant la solution.

Pour obtenir les équations élémentaires, plusieurs approches sont disponibles:

une approche modèle physique: on définit sur chaque élément un modèle physique simple, p.e. un système masse-ressort en mécanique. C’est ce qui sera développé dans le chapitre suivant sur la pale d’éolienne.
une approche plus mathématique, mais plus générale, basée sur une formulation faible (ou variationnelle), qui sera développé dans la suite.

1.4.3. Avantages#

Flexibilité géométrique : adapté aux formes complexes et aux irrégularités.
Adaptabilité : raffinement local (h‑refinement) ou augmentation du degré des fonctions (p‑refinement).
Large applicabilité : mécanique, thermique, mécanique des fluides, électromagnétisme, etc.
Matériau et non linéarité : supporte les matériaux non linéaires et les problèmes itératifs.

1.4.4. Inconvénients#

Coût de calcul : grand nombre de nœuds → matrices volumineuses et souvent creuse (sparse).
Qualité du maillage : un maillage de qualité est essentiel pour la précision.
Conditionnement : dans certain cas les matrices sont mal conditionnées et peuvent ralentir les solveurs.
Complexité : mise en œuvre, choix des éléments, gestion des contraintes, et vérification de la convergence.

Étape	Action	Objectif
1. Maillage	Diviser le domaine (\(\omega\)) en un ensemble d’éléments simples (triangles, quadrilatères, tétraèdres, etc.).	Réduire le problème continu à une structure discrète.
2. Fonctions de forme	Choisir des fonctions locales \(N_i(x)\) (généralement polynomiales) qui interpolent la solution à l’intérieur d’un élément.	Relier les valeurs aux nœuds aux valeurs continues dans l’élément.
3. Approximation globale	Représenter la solution comme combinaison linéaire des fonctions de forme pondérées par les inconnues nodales : \(u_h(x)=\sum_{i} N_i(x) u_i\).	Convertir le problème différentiel en système d’équations algébriques.
4. Équations élémentaires	Substituer l’approximation dans l’équation différentielle et effectuer l’intégration sur chaque élément.	Obtenir la matrice d’élément \(K^{e}\) et le vecteur de force \(f^{e}\).
5. Assemblage	Assembler les matrices et vecteurs locaux en une matrice globale (\(K\)) et un vecteur global (\(f\)).	Respecter la continuité entre les éléments et tenir compte de toutes les contraintes.
6. Conditions aux limites	Imposer les contraintes (déplacements fixes, flux, etc.) sur le périmètre.	Modifier le système global (remplir, supprimer, ou ajuster des lignes/colonnes).
7. Résolution	Résoudre le système linéaire \(KU = f\) (ou itératif pour les non linéaires).	Obtenir les valeurs nodales \(U=\{u_i\}\) qui approximant la solution.