3. Formulation faible et formulation variationnelle

3.1. Une première approche en statique

On considère une poutre encastrée à une extrémité et soumise à une force de traction \(F\) dans la direction \(x\)

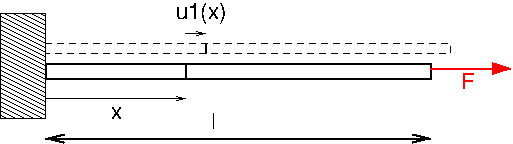
Fig. 3.1 poutre en traction

Comme il a été vue dans le chapitre précédent, l’équation d’équilibre locale des forces en statique s’écrit ( en notant \(u_{1}(x)\) le déplacement d’une section d’abscisse \(x\) , \(S\) la section et \(E\) le module d’Young):

(3.1)\[\frac{\partial}{\partial x}\left(ES\frac{\partial u_{1}}{\partial x}\right)=0\]

A cette équation, il faut ajouter 2 conditions aux limites:

1. la condition d’encastrement en \(x=0\) (condition de Dirichlet):

   (3.2)\[\begin{aligned} u_{1}(0) & = & 0\end{aligned}\]

2. la condition de force imposée en \(x=l\) (condition de Neumann):

   (3.3)\[ES\left(\frac{\partial u_{1}}{\partial x}\right)_{x=l}=F\]

Cette formulation du problème correspond à la formulation classique d’équilibre local, qui traduit le principe fondamental de la mécanique \(\overrightarrow{F}=m\overrightarrow{\gamma}\). En utilisant le principe des travaux virtuels, on peut écrire une formulation intégrale équivalente. Pour cela on considère un déplacement « virtuel » licite \(\delta u_{1}\)autour de la position d’équilibre, et on calcul le travail des forces associées à ce déplacement. On multiplie donc l’équation (3.1) par \(\delta u_{1}\) et on intègre dans le domaine pour calculer la somme des travaux dans le solide:

\[\int_{0}^{l}\frac{\partial}{\partial x}\left(ES\frac{\partial u_{1}}{\partial x}\right)\delta u_{1}dx=0\]

En intégrant par partie, il vient:

\[\int_{0}^{l}ES\frac{\partial u_{1}}{\partial x}\frac{\partial\delta u_{1}}{\partial x}dx=\left[ES\frac{\partial u_{1}}{\partial x}\delta u_{1}\right]_{0}^{l}\]

On calcule ensuite le terme de bord en utilisant les conditions aux limites. La condition de Neumann (3.3) permet de calculer ce terme en \(x=l\). Pour le terme en \(x=0\) , on note que le déplacement \(\delta u_{1}\)est un déplacement licite, qui doit respecter les liaisons. La condition de Dirichlet fixe la valeur de \(u_{1}\) en \(x=0\), et donc le déplacement \(\delta u_{1}\)doit s’annuler en \(x=0\): \(\delta u_{1}(0)=0\). On obtient ainsi:

(3.4)\[\underbrace{\int_{0}^{l}ES\frac{\partial u_{1}}{\partial x}\frac{\partial\delta u_{1}}{\partial x}dx}_{\mbox{travail des forces internes}}=\underbrace{F\delta u_{1}(l)}_{\mbox{travail des forces externes}}\]

Cette équation traduit le principe des travaux virtuels appliquée au solide:

principe des travaux virtuels

La somme du travail des forces internes ( contraintes \(\sigma_{xx}\)) est égale à la somme du travail fourni par les forces externes (force de traction \(F\)) pour tous les déplacements virtuels licites vérifiant les liaisons \(\delta u_{1}(0)=0\).

C’est la formulation faible de l’équation (3.1) associée aux conditions aux limites (3.2) et (3.3) qui s’écrit:

(3.5)\[\begin{split}\left\{ \begin{array}{l} \mbox{Trouvez }u_{1}(x)\mbox{ t.q.}\,u_{1}(0)=0\\ \int_{0}^{l}ES\frac{\partial u_{1}}{\partial x}\frac{\partial\delta u_{1}}{\partial x}dx=F\,\delta u_{1}(l)\,\,\,\,\forall\delta u_{1}\,\mbox{ t.q. }\delta u_{1}(0)=0 \end{array}\right.\end{split}\]

En utilisant le calcul des variations, on peut donner une interprétation de l’équation (3.4). En effet cette équation s’écrit sous la forme suivante:

\[\delta\left(\frac{1}{2}\int_{0}^{l}ES\left(\frac{\partial u_{1}}{\partial x}\right)^{2}dx\right)=\delta\left(Fu_{1}(l)\right)\]

Cette équation traduit la condition de stationnarité ou d’extremum de la quantité \(J(u_{1})\)

(3.6)\[J(u_{1})=\underbrace{\frac{1}{2}\int_{0}^{l}ES\left(\frac{\partial u_{1}}{\partial x}\right)^{2}dx}_{U}-\underbrace{Fu_{1}(l)}_{W}\]

Cette quantité \(J(u_{1})\) représente la somme de l’énergie élastique \(U\) du solide et du travail « virtuel » \(W\) des forces extérieures appliquées. Pour ce problème statique, on peut calculer l’énergie élastique \(U\) à l’équilibre en utilisant la formulation faible (3.5). En effet, le déplacement \(u_{1}\) et sa variation \(\delta u_{1}\)vérifient les mêmes conditions aux limites, donc parmi toutes les variations virtuelles licites \(\delta u_{1}\), on peut choisir \(\delta u_{1}=u_{1}\) dans (3.5). On obtient ainsi:

\[\int_{0}^{l}ES\left(\frac{\partial u_{1}}{\partial x}\right)^{2}dx=Fu_{1}(l)\]

d’où l’expression du potentiel à l’équilibre:

\[U=\frac{1}{2}\int_{0}^{l}ES\left(\frac{\partial u_{1}}{\partial x}\right)^{2}dx=\frac{1}{2}Fu_{1}(l)=\frac{1}{2}W\]

L’énergie élastique à l’équilibre est donc égale à la moitié du travail de la force \(F\) pour un déplacement \(u_{1}(l)\). C’est l’énergie fournie au solide, lorsque que l’on passe de l’état naturel (i.e. sans contraintes) avec \(F=0\) à l’état contraint par la force \(F\). Ce passage doit se faire par une succession d’états d’équilibre correspondant à des petites augmentations \(\delta F\) de la force pour passer de \(0\) à \(F\). Dans ce cas le travail fourni est égale à la valeur moyenne \(\frac{F}{2}\) de la force (entre 0 et \(F\)) multipliée par le déplacement \(u(l)\). Ce travail fourni est emmagasiné dans le solide sous forme de potentiel élastique. C’est ce que traduit la relation précédente.

On note que la formulation faible ne donne pas le travail réel des forces, mais uniquement un travail virtuel autour de la position d’équilibre pour une variation virtuelle licite autour de cette position. En effet l’équilibre des forces implique l’égalité des travaux de ces forces pour un petit déplacement autour de la position d’équilibre.

A partir de ces relations, on peut en déduire la valeur de la fonctionnelle \(J(u_{1})\) à l’équilibre, qui est égale à l’opposé de l’énergie élastique:

\[J(u_{1})=U-W=-U\]

La condition de stationnarité de \(J(u_{1})\), qui dans ce cas est un minimum, correspond à la formulation variationnelle de l’équation (3.1) associée aux conditions aux limites (3.2) et (3.3), et s’écrit:

(3.7)\[\begin{split}\left\{ \begin{array}{l} \mbox{Trouvez }u_{1}(x)\,\mbox{ t.q }\,u_{1}(0)=0\\ \begin{array}{l} \mbox{ minimisant }\,J(u)\\ J(u_{1})\le J(u)\,\,\forall v(x)\,\mbox{ t.q. }\,u(0)=0 \end{array}\\ \mbox{ avec }\,J(u)=\frac{1}{2}\int_{0}^{l}ES\left(\frac{\partial u}{\partial x}\right)^{2}dx-Fu(l) \end{array}\right.\end{split}\]

Pour un même problème, on a donc 3 formulations équivalentes:

1. la formulation locale des équations d’équilibre:
   c’est une équation aux dérivées partielles (3.1) associée à des conditions aux limites (3.2) et (3.3).

2. la formulation faible ou principe des travaux virtuels:
   c’est une formulation intégrale (3.5) traduisant l’équilibre des travaux des forces appliquées

3. la formulation variationnelle ou principe de stationnarité:
   c’est un problème d’extremum (3.7) (de minimisation ou de maximisation suivant le signe de \(J(u)\)[1]) traduisant à l’équilibre un principe de stationnarité de l’énergie du système.

Suivant les problèmes, l’une ou l’autre formulation peut être la plus appropriée. Cependant l’approximation par éléments finis nécessite l’écriture de la formulation faible ou variationnelle du problème.

3.1.1. remarques

D’un point de vue mathématique, la formulation faible est la formulation la plus générale, car elle s’applique à n’importe quelle équation aux dérivées partielles. Elle permet en outre l’accès à des solutions généralisées (ou solutions faibles) des équations aux dérivées partielles. C’est la théorie de l’analyse fonctionnelle et des espaces de Hilbert (voir la bibliographie).

3.2. Une seconde approche en dynamique

Considérons maintenant le problème de la vibration libre de la poutre encastrée précédente. En ajoutant le terme accélération, l’équation d’équilibre s’écrit:

(3.8)\[\rho S\frac{\partial^{2}u_{1}}{\partial t^{2}}-\frac{\partial}{\partial x}\left(ES\frac{\partial u_{1}}{\partial x}\right)=0\]

à laquelle on ajoute les conditions aux limites:

(3.9)\[u_{1}(0,t)=0,\,\,ES\frac{\partial u_{1}}{\partial x}(l,t)=0\]

et les conditions initiales (déformée \(u_{0}\) à \(t=0\) et vitesse initiale nulle):

(3.10)\[u_{1}(x,0)=u_{0}(x),\,\,\frac{\partial u_{1}}{\partial t}=0\]

La formulation faible s’obtient comme précédemment, en multipliant l’équation par un déplacement virtuel licite \(\delta u_{1}\) (à un instant t fixé) et en intégrant sur tout le solide:

\[\int_{0}^{l}\rho S\frac{\partial^{2}u_{1}}{\partial t^{2}}\delta u_{1}dx\,-\,\int_{0}^{l}\frac{\partial}{\partial x}\left(ES\frac{\partial u_{1}}{\partial x}\right)\delta u_{1}dx=0\]

Après intégration par partie du second terme, il vient:

\[\int_{0}^{l}\rho S\frac{\partial^{2}u_{1}}{\partial t^{2}}\delta u_{1}dx\,+\,\int_{0}^{l}ES\frac{\partial u_{1}}{\partial x}\frac{\partial\delta u_{1}}{\partial x}dx=\left[ES\frac{\partial u_{1}}{\partial x}\delta u_{1}\right]_{0}^{l}\]

En utilisant les conditions aux limites (3.9), la variation \(\delta u_{1}\)doit s’annuler en \(x=0\): \(\delta u_{1}(0)=0\) .

(3.11)\[\int_{0}^{l}\rho S\frac{\partial^{2}u_{1}}{\partial t^{2}}\delta u_{1}dx\,+\,\int_{0}^{l}ES\frac{\partial u_{1}}{\partial x}\frac{\partial\delta u_{1}}{\partial x}dx=0\]

Cette formulation faible s’écrit:

(3.12)\[\begin{split}\left\{ \begin{array}{l} \mbox{Trouvez }u_{1}(x,t)\,\mbox{ t.q. à chaque instant t }\,u_{1}(0,t)=0\\ \int_{0}^{l}\rho S\frac{\partial^{2}u_{1}}{\partial t^{2}}\delta u_{1}dx\,+\int_{0}^{l}ES\frac{\partial u_{1}}{\partial x}\frac{\partial\delta u_{1}}{\partial x}dx=0\,\,\,\,\forall\delta u_{1}\,\mbox{ t.q. }\delta u_{1}(0)=0 \end{array}\right.\end{split}\]

Dans cette formulation faible, on a considéré une variation \(\delta u_{1}(x)\) à un instant t donné. Cette équation traduit l’égalité à chaque instant t du travail des forces d’accélération et des forces élastiques.

Pour écrire la formulation variationnelle, on considéré ce qu’il se passe entre 2 instants: l’instant initial \(t=0\) et un instant \(t=\tau\). Les 2 positions d’équilibres associées sont notées \(u_{1}(x,t=0)\) et \(u_{1}(x,t=\tau)\), et on recherche quelles sont les différentes solutions possibles \(u(x,t)\) entre ces 2 instants. Les différentes trajectoires (solutions) licites considérées \(u(x,t)\) coïncident avec les 2 états d’équilibres à \(t=0\) et à \(t=\tau\):

\[u(x,0)=u_{1}(x,0)\,\,\mbox{ et }\,\,u(x,\tau)=u_{1}(x,\tau)\]

et vérifient les liaisons \(u(0,t)=0\)

La variation entre la solution d’équilibre et une de ces trajectoires : \(\delta u_{1}=u_{1}(x,t)-u(x,t)\), vérifie donc:

(3.13)\[\delta u_{1}(x,0)=0,\,\,\delta u_{1}(x,\tau)=0\]

et la condition de liaison \(\delta u(0,t)=0\).

Pour obtenir la formulation variationnelle, on intègre en temps l’équation (3.11) entre l’instant initial et l’instant \(\tau\):

(3.14)\[\int_{0}^{\tau}\left(\int_{0}^{l}\rho S\frac{\partial^{2}u_{1}}{\partial t^{2}}\delta u_{1}dx\,+\,\int_{0}^{l}ES\frac{\partial u_{1}}{\partial x}\frac{\partial\delta u_{1}}{\partial x}dx\right)dt=0\]

En intégrant par partie la dérivée seconde en temps, il vient:

\[\int_{0}^{\tau}\frac{\partial^{2}u_{1}}{\partial t^{2}}\delta u_{1}d\tau=-\int_{0}^{\tau}\frac{\partial u_{1}}{\partial t}\frac{\partial\delta u_{1}}{\partial t}d\tau+\left[\frac{\partial u_{1}}{\partial t}\delta u_{1}\right]_{0}^{\tau}\]

Les conditions imposées sur la variation (3.13) impliquent la nullité du terme de bord, et l’équation (3.14) devient:

\[\int_{0}^{\tau}\delta\left(\frac{1}{2}\int_{0}^{l}\rho S\left(\frac{\partial u_{1}}{\partial t}\right)^{2}dx\,-\,\frac{1}{2}\int_{0}^{l}ES\left(\frac{\partial u_{1}}{\partial x}\right)^{2}dx\right)dt=0\]

En notant

\[\mathcal{L}(u_{1},\dot{u}_{1})=\underbrace{\frac{1}{2}\int_{0}^{l}\rho S\left(\frac{\partial u_{1}}{\partial t}\right)^{2}dx}_{T=\mbox{énergie cinétique}}\,-\,\underbrace{\frac{1}{2}\int_{0}^{l}ES\left(\frac{\partial u_{1}}{\partial x}\right)^{2}dx}_{U=\mbox{énergie potentielle}}\]

on obtient:

\[\delta\int_{0}^{\tau}\mathcal{L}(u_{1},\dot{u}_{1})\,dt=0\]

Cette relation implique que la solution \(u_{1}\) doit être telle que \(\mathcal{A}=\int_{0}^{\tau}\mathcal{L}(u_{1},\dot{u}_{1})\,dt\) soit extremum. En terme mécanique, cette intégrale représente une action, et la fonctionnelle \(\mathcal{L}(u_{1},\dot{u}_{1})\) le Lagrangien du système. En effet la fonctionnelle \(\mathcal{L}(u_{1},\dot{u}_{1})=T-U\) est la différence entre l’énergie cinétique \(T\) du solide et son énergie potentielle élastique \(U\). Elle représente le Lagrangien du système, et l’équation précédente est la traduction du principe de moindre action en mécanique:

principe de moindre action

la solution d’équilibre du système \(u_{1}(x,t)\) est telle que l’action \(\mathcal{A}=\int_{0}^{\tau}\mathcal{L}(u_{1},\dot{u}_{1})\,dt\) soit minimum.

L’action \(\mathcal{A}\) est une fonctionnelle (i.e. est fonction d’une fonction \(u_{1}(x,t)\)). La condition de minimisation de \(\mathcal{A}\) est donc que sa « dérivée par rapport » à \(u_{1}\) s’annule (généralisation de la condition d’extremum d’une fonction). La définition de la dérivée fonctionnelle de \(\mathcal{A}\) est une généralisation de la dérivée d’une fonction par rapport à une variable, et est fonction de la variation (direction de dérivation) \(\delta u_{1}\).

\[<\frac{d\mathcal{A}}{du_{1}},\delta u_{1}>=\lim_{\lambda\rightarrow0}\frac{\mathcal{A}(u_{1}+\lambda\delta u_{1})-\mathcal{A}(u_{1})}{\lambda}\]

En utilisant cette définition, et en utilisant un calcul classique de variation, la condition de minimisation de l’action conduit aux équations de Lagrange pour un milieu continu.

Pour un système discret à \(N\) degrés de liberté, la fonction inconnue \(u_{1}\) est un vecteur à N composantes \(\left\{ q_{i}\right\}\), et on obtient alors les \(N\) équations de Lagrange:

\[\frac{d}{dt}\left(\frac{\partial\mathcal{L}}{\partial\dot{q}_{i}}\right)-\frac{\partial\mathcal{L}}{\partial q_{i}}=0\,\,\,\mbox{pour }i=1,N\]

Pour un système continu, on obtient les équations de Lagrange:

\[<\frac{d}{dt}\left(\frac{\partial\mathcal{L}}{\partial\dot{u}_{1}}\right)-\frac{\partial\mathcal{L}}{\partial u_{1}}\,,\,\delta u_{1}>=0\,\,\,\forall\delta u_{1}\,\mbox{ licite}\]

qui correspondent à la formulation faible (3.12), ou principe des travaux virtuels.

A partir de ce formalisme Lagrangien, on peut retrouver les propriétés du système. On définit la quantité \(\mathcal{E}(u_{1},\dot{u}_{1})\) par

\[\mathcal{E}(u_{1},\dot{u}_{1})=\frac{\partial\mathcal{L}}{\partial\dot{u}_{1}}\dot{u}_{1}-\mathcal{L}\]

Cette quantité reste constante au cours du temps

\[\mathcal{E}(u_{1},\dot{u}_{1})=cste\]

puisque par définition de \(\mathcal{E}(u_{1},\dot{u}_{1})\)

\[\begin{split}\begin{aligned} \frac{d}{dt}\mathcal{E}(u_{1},\dot{u}_{1}) & = & \frac{\partial\mathcal{L}}{\partial\dot{u}_{1}}\ddot{u}_{1}+\frac{d}{dt}\left(\frac{\partial\mathcal{L}}{\partial\dot{u}_{1}}\right)\dot{u}_{1}-\frac{d}{dt}\left(\mathcal{L}\right)\\ & = & \frac{\partial\mathcal{L}}{\partial\dot{u}_{1}}\ddot{u}_{1}-+\frac{d}{dt}\left(\frac{\partial\mathcal{L}}{\partial\dot{u}_{1}}\right)\dot{u}_{1}-\left(\frac{\partial\mathcal{L}}{\partial\dot{u}_{1}}\ddot{u}_{1}+\frac{\partial\mathcal{L}}{\partial u_{1}}\dot{u}_{1}\right)\\ & = & <\frac{d}{dt}\left(\frac{\partial\mathcal{L}}{\partial\dot{u}_{1}}\right)-\frac{\partial\mathcal{L}}{\partial u_{1}}\,,\,\dot{u}_{1}>\end{aligned}\end{split}\]

Cette dernière expression est nulle, puisque \(\mathcal{L}(u_{1},\dot{u}_{1})\) vérifie les équations de Lagrange (3.12). Cette quantité \(\mathcal{E}(u_{1},\dot{u}_{1})=2T-\mathcal{L}=T+U\) est en faite l’énergie totale du système:

\[\mathcal{E}(u_{1},\dot{u}_{1})=\underbrace{\frac{1}{2}\int_{0}^{l}\rho S\left(\frac{\partial u_{1}}{\partial t}\right)^{2}dx}_{T=\mbox{énergie cinétique}}\,+\,\underbrace{\frac{1}{2}\int_{0}^{l}ES\left(\frac{\partial u_{1}}{\partial x}\right)^{2}dx}_{U=\mbox{énergie potentielle}}\]

qui se conserve au cours du temps. Pour ce système conservatif, on retrouve donc le principe de conservation de l’énergie.

La formulation variationnelle de notre problème s’écrit:

\[\begin{split}\left\{ \begin{array}{l} \mbox{Trouver }u_{1}(x,t)\,\mbox{ t.q. }\,u_{1}(0,t)=0\\ \mbox{minimisant l'action }\mathcal{A}=\int_{0}^{\tau}\mathcal{L}(u_{1},\dot{u}_{1})\,dt \end{array}\right.\end{split}\]

La condition de minimisation de l’action conduit aux équations de Lagrange:

\[<\frac{d}{dt}\left(\frac{\partial\mathcal{L}}{\partial\dot{u}_{1}}\right)-\frac{\partial\mathcal{L}}{\partial u_{1}}\,,\,\delta u_{1}>=0\]

qui correspondent la formulation faible (3.12), ou principe des travaux virtuels

\[\begin{split}\left\{ \begin{array}{l} \mbox{Trouver }u_{1}(x,t)\,\mbox{ t.q. à chaque instant t}\\ <\frac{d}{dt}\left(\frac{\partial\mathcal{L}}{\partial\dot{u}_{1}}\right)-\frac{\partial\mathcal{L}}{\partial u_{1}}\,,\,\delta u_{1}>=0\,\,\forall\delta u_{1}\,\mbox{licite} \end{array}\right.\end{split}\]

3.2.1. Élasticité linéaire

Pour un problème dynamique en élasticité linéaire, utilisant une formulation en déplacement \(\overrightarrow{\mathbf{U}}\), le Lagrangien s’écrit sous la forme:

\[\mathcal{L}(\overrightarrow{\mathbf{U}},\overrightarrow{\dot{\mathbf{U}}})=\underbrace{\frac{1}{2}\int_{\Omega}\rho\frac{\partial\overrightarrow{\dot{\mathbf{U}}}}{\partial t}.\frac{\partial\overrightarrow{\dot{\mathbf{U}}}}{\partial t}\,dv}_{T}\,-\,\underbrace{\frac{1}{2}\int_{\Omega}\overrightarrow{\sigma}\otimes\overrightarrow{\varepsilon}\,dv}_{U}+\,\underbrace{\int_{\Omega}\rho\,\overrightarrow{f}.\overrightarrow{\mathbf{U}}\,dv}_{W_{1}}+\underbrace{\int_{\Gamma}\rho\,\overrightarrow{F}.\overrightarrow{\mathbf{U}}\,ds}_{W_{2}}\]

et comprend l’énergie cinétique \(T\), l’énergie potentielle élastique \(U\) (qui est le produit tensoriel du tenseur des contraintes et du tenseur des déformations), le travail des forces volumiques externes \(\overrightarrow{f}\) et le travail des forces surfaciques externes[3] \(\overrightarrow{F}\).

En utilisant la loi de comportement élastique, et la définition du tenseur des déformations:

\[\overrightarrow{\sigma}=\mathbf{D}\,\overrightarrow{\varepsilon}\,\,\,,\,\,\,\overrightarrow{\varepsilon}=\frac{1}{2}(\overrightarrow{\mathbf{gra}}\mathbf{d}\,\overrightarrow{\mathbf{U}}\,+\overrightarrow{\mathbf{gra}}\mathbf{d}^{t}\,\overrightarrow{\mathbf{U}}\,)\]

l’énergie élastique s’écrit en fonction du déplacement sous la forme:

\[U=\frac{1}{2}\int_{\Omega}\left(\frac{1}{2}(\overrightarrow{\mathbf{gra}}\mathbf{d}\,\overrightarrow{\mathbf{U}}\,+\overrightarrow{\mathbf{gra}}\mathbf{d}^{t}\,\overrightarrow{\mathbf{U}}\,)\right)^{t}\,\mathbf{D}\,\left(\frac{1}{2}(\overrightarrow{\mathbf{gra}}\mathbf{d}\,\overrightarrow{\mathbf{U}}\,+\overrightarrow{\mathbf{gra}}\mathbf{d}^{t}\,\overrightarrow{\mathbf{U}}\,)\right)\,dv\]

Les équations de Lagrange s’écrivent alors:

\[<\frac{d}{dt}\left(\frac{\partial\mathcal{L}}{\partial\dot{u}_{i}}\right)-\frac{\partial\mathcal{L}}{\partial u_{i}}\,,\,\delta u_{i}>=0\,\,\,\mbox{ pour }i=1,3\]

3.2.2. Problème statique

Dans le cas d’un problème statique: \(\dot{u}_{1}=\frac{\partial u_{1}}{\partial t}=0\), le Lagrangien ne dépendant que de \(u_{1}(x)\), et s’écrit ( en tenant compte du terme de force extérieure \(F\)):

\[\mathcal{L}(u_{1})=\underbrace{Fu_{1}(l)}_{\mbox{travail des forces extérieures}}\,\,-\,\,\underbrace{\frac{1}{2}\int_{0}^{l}ES\left(\frac{\partial u_{1}}{\partial x}\right)^{2}dx}_{\mbox{énergie élastique}}\]

Il correspond donc à l’opposée de la fonctionnelle \(J\) (3.6) : \(\mathcal{L}(u_{1})=-J(u_{1})\). La formulation faible (3.5) correspond donc bien aux équations de Lagrange à l’équilibre statique:

\[<\frac{\partial\mathcal{L}}{\partial u_{1}}\,,\,\delta u_{1}>=0\,\,\forall\delta u_{1}\]

3.2.3. Système dynamique amorti

Dans le cas d’un système mécanique amorti, on introduit une force supplémentaire d’amortissement \(F_{a}\), en général dépendant de la vitesse \(\dot{u}_{1}\). Cette force n’est pas conservative, et on ne peut plus définir de Lagrangien \(\mathcal{L}(u_{1},\dot{u}_{1})\) pour le système complet et écrire les équations de Lagrange (3.12) .

En revenant au principe des travaux virtuels, on calcule le travail « virtuel » de la force d’amortissement:

\[\int_{0}^{l}F_{a}(\dot{u}_{1}).\delta u_{1}dx\]

et en utilisant le Lagrangien précédent pour la partie conservative

\[\mathcal{L}(u_{1},\dot{u}_{1})=\frac{1}{2}\int_{0}^{l}\rho S\left(\frac{\partial u_{1}}{\partial t}\right)^{2}dx\,-\,\frac{1}{2}\int_{0}^{l}ES\left(\frac{\partial u_{1}}{\partial x}\right)^{2}dx\]

on obtient les équations de Lagrange généralisées, ou principe des travaux virtuels

\[<\frac{d}{dt}\left(\frac{\partial\mathcal{L}}{\partial\dot{u}_{1}}\right)-\frac{\partial\mathcal{L}}{\partial u_{1}}\,,\,\delta u_{1}>+\int_{0}^{l}F_{a}(\dot{u}_{1}).\delta u_{1}dx=0\,\,\forall\delta u_{1}\,\mbox{licite}\]

Dans ce cas, on ne peut plus appliquer de principe de moindre action ou formulation variationnelle. On dispose uniquement de la formulation faible, ou principe des travaux virtuels.

3.2.3.1. Exercice 1:

Écrire la formulation faible dans le cas de vibrations forcées induites par une force dépendant du temps \(F(t)\) appliquée en \(x=l\) .

On pourra montrer que dans ce cas le Lagrangien s’écrit:

\[\mathcal{L}(u_{1},\dot{u}_{1})=\frac{1}{2}\int_{0}^{l}\rho S\left(\frac{\partial u_{1}}{\partial t}\right)^{2}dx\,-\,\frac{1}{2}\int_{0}^{l}ES\left(\frac{\partial u_{1}}{\partial x}\right)^{2}dx+Fu_{1}(l)\]

3.2.3.2. Exercice 2:

Écrire la formulation faible dans le cas où le système précédent est amorti, avec un amortissement intrinsèque proportionnel à la masse. Dans une section d’épaisseur \(dx\) la force d’amortissement s’écrit:

\[-\frac{\rho Sdx}{\tau}\,\frac{\partial u_{1}}{\partial t}\]

Montrez que les équations de Lagrange s’écrivent:

\[\int_{0}^{l}\rho S\frac{\partial^{2}u_{1}}{\partial t^{2}}\delta u_{1}dx\,+\int_{0}^{l}ES\frac{\partial u_{1}}{\partial x}\frac{\partial\delta u_{1}}{\partial x}dx+\int_{0}^{l}\frac{\rho S}{\tau}\left(\frac{\partial u_{1}}{\partial t}\right)\delta u_{1}dx=Fu_{1}(l)\,\,\,\forall\delta u_{1}\,\mbox{licite}\]

3.3. Formulation faible en mécanique des fluides

Considérons l’écoulement d’un fluide incompressible très visqueux dans une cavité carrée \(\Omega=[0,L][0,L]\) dont la partie supérieure est mise en mouvement (figure ci-dessous). Par entraînement visqueux, le fluide se met en mouvement dans la cavité pour former un tourbillon.

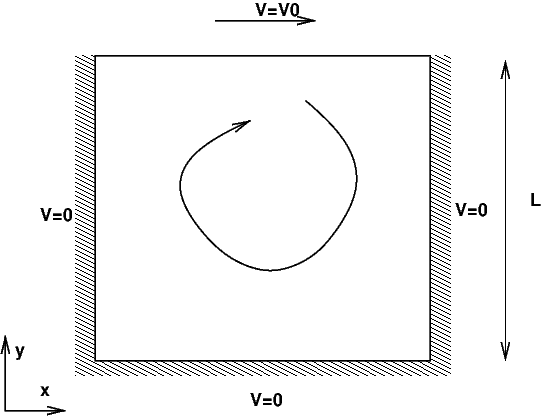
Fig. 3.2 écoulement dans une cavité

En considérant le problème comme plan, les équations d’équilibre sont les équations de Stockes:

(3.15)\[\begin{split}\begin{aligned} \frac{\partial v_{1}}{\partial x}+\frac{\partial v_{2}}{\partial y} & = & 0\\ -\frac{\mu}{\rho}\left(\frac{\partial^{2}v_{1}}{\partial x^{2}}+\frac{\partial^{2}v_{1}}{\partial y^{2}}\right) & = & -\frac{1}{\rho}\frac{\partial p}{\partial x}\\ -\frac{\mu}{\rho}\left(\frac{\partial^{2}v_{2}}{\partial x^{2}}+\frac{\partial^{2}v_{2}}{\partial y^{2}}\right) & = & -\frac{1}{\rho}\frac{\partial p}{\partial y}\end{aligned}\end{split}\]

auxquels on ajoute les conditions aux limites d’adhérence aux parois:

(3.16)\[\overrightarrow{\mathbf{V}}(x,L)=[V_{0},0],\,\,\,\,\overrightarrow{\mathbf{V}}(x,0)=\overrightarrow{\mathbf{V}}(0,y)=\overrightarrow{\mathbf{V}}(L,y)=\overrightarrow{\mathbf{0}}\]

Pour écrire la formulation faible de ce système on considère à un instant t une variation de vitesse \(\delta\overrightarrow{\mathbf{V}}\) . Cette variation doit être licite, i.e. si on fixe la valeur de la vitesse (condition de Dirichlet), la variation s’annule (condition de Dirichlet homogène):

(3.17)\[\delta\overrightarrow{\mathbf{V}}(x,L)=\delta\overrightarrow{\mathbf{V}}(x,0)=\delta\overrightarrow{\mathbf{V}}(0,y)=\delta\overrightarrow{\mathbf{V}}(L,y)=\overrightarrow{\mathbf{0}}\]

Les équations d’équilibre (3.15) sont la projection de l’équation vectorielle:

\[-\frac{\mu}{\rho}\,\overrightarrow{\mathbf{div}}\left(\overrightarrow{\mathbf{grad}}\,\overrightarrow{\mathbf{V}}\right)=-\overrightarrow{grad}\,p\]

que nous multiplions donc scalairement par \(\delta\overrightarrow{\mathbf{V}}\) et intégrons sur le domaine \(\Omega\) pour obtenir la puissance virtuelle des forces appliquées pour une variation \(\delta\overrightarrow{\mathbf{V}}\) de la vitesse:

\[-\int_{\Omega}\frac{\mu}{\rho}\,\overrightarrow{\mathbf{div}}\left(\overrightarrow{\mathbf{grad}}\,\overrightarrow{\mathbf{V}}\right)\cdot\delta\overrightarrow{\mathbf{V}}\,dxdy=-\int_{\Omega}\overrightarrow{grad}\,p\cdot\delta\overrightarrow{\mathbf{V}}\,dxdy\]

En intégrant par partie les 2 termes il vient:

\[\begin{split}\begin{aligned} \int_{\Omega}\frac{\mu}{\rho}\,\overrightarrow{\mathbf{grad}}\,\overrightarrow{\mathbf{V}}\otimes\overrightarrow{\mathbf{grad}}\,\delta\overrightarrow{\mathbf{V}}\,dxdy\,-\,\int_{\Gamma}\frac{\mu}{\rho}\left(\overrightarrow{\mathbf{grad}}\,\overrightarrow{\mathbf{V}}\times\overrightarrow{n}\right)\cdot\delta\overrightarrow{\mathbf{V}}\,d\Gamma & =\\ \int_{\Omega}p\,div\left(\delta\overrightarrow{\mathbf{V}}\right)\,dxdy-\int_{\Gamma}p\,\overrightarrow{n}\cdot\delta\overrightarrow{\mathbf{V}}\,d\Gamma\end{aligned}\end{split}\]

En utilisant les conditions (3.17) imposées à \(\delta\overrightarrow{\mathbf{V}}\): \(\left(\delta\overrightarrow{\mathbf{V}}\right)_{\Gamma}=\overrightarrow{0}\), les intégrales de bord s’annulent et il reste:

(3.18)\[\int_{\Omega}\frac{\mu}{\rho}\,\overrightarrow{\mathbf{grad}}\,\overrightarrow{\mathbf{V}}\otimes\overrightarrow{\mathbf{grad}}\,\delta\overrightarrow{\mathbf{V}}\,dxdy=\int_{\Omega}p\,div\left(\delta\overrightarrow{\mathbf{V}}\right)\,dxdy\]

3.3.1. Première formulation faible du problème de Stockes

Si on impose de plus à la variation \(\delta\overrightarrow{\mathbf{V}}\) d’être incompressible: \(div\,\delta\overrightarrow{\mathbf{V}}=0\), on obtient une première formulation faible du problème:

(3.19)\[\begin{split}\left\{ \begin{array}{c} \mbox{Trouvez }\,\overrightarrow{\mathbf{V}}\,t.q.\,div\,\overrightarrow{\mathbf{V}}=0\,\mbox{ + CL{eq}`eq2.25`}\\ \int_{\Omega}\frac{\mu}{\rho}\,\overrightarrow{\mathbf{grad}}\,\overrightarrow{\mathbf{V}}\otimes\overrightarrow{\mathbf{grad}}\,\delta\overrightarrow{\mathbf{V}}\,dxdy=0\,\,\forall\delta\overrightarrow{\mathbf{V}}\,t.q.\,div\,\delta\overrightarrow{\mathbf{V}}=0\,\mbox{ et CL {eq}`2.24`} \end{array}\right.\end{split}\]

L’équation intégrale projetée sur les 2 axes \((ox,oy)\) s’écrit aussi:

\[\begin{split}\begin{aligned} \int_{\Omega}\frac{\mu}{\rho}\,\left(\frac{\partial v_{1}}{\partial x}\frac{\partial\delta v_{1}}{\partial x}+\frac{\partial v_{1}}{\partial y}\frac{\partial\delta v_{1}}{\partial y}\right)\,dxdy & = & 0\,\,\forall\delta v_{1}\\ \int_{\Omega}\frac{\mu}{\rho}\,\left(\frac{\partial v_{2}}{\partial x}\frac{\partial\delta v_{2}}{\partial x}+\frac{\partial v_{2}}{\partial y}\frac{\partial\delta v_{2}}{\partial y}\right)\,dxdy & = & 0\,\,\forall\delta v_{2}\end{aligned}\end{split}\]

Cette formulation faible traduit le fait que la somme des puissances des forces visqueuses doit être nulle pour toute variation de vitesse \(\delta\overrightarrow{\mathbf{V}}\) licite et incompressible . On constate que la pression n’intervient plus dans cette formulation, puisque que la puissance des forces de pression est automatiquement nulle pour une variation de vitesse \(\delta\overrightarrow{\mathbf{V}}\) licite et incompressible. On retrouve l’interprétation classique du champ de pression dans un écoulement de fluide incompressible: la pression \(p\) sert à maintenir le champ de vitesse incompressible ( i.e. \(div\,\overrightarrow{\mathbf{V}}=0\)). Dans la formulation variationnelle (3.19), on impose au champ de vitesse et à sa variation de rester incompressible, et donc on élimine la pression du problème. On constate que l’élimination de la pression a aussi découplée les équations de vitesse. Attention cependant, ce découplage n’est que relatif, puisque la condition d’incompressibilité couple les composantes de vitesse.

Cette formulation faible découle d’un problème variationnelle, puisque pour ce problème on peut définir un Lagrangien:

\[\mathcal{L}(v_{1},v_{2})=\frac{1}{2}\int_{\Omega}\frac{\mu}{\rho}\,\left(\left(\frac{\partial v_{1}}{\partial x}\right)^{2}+\left(\frac{\partial v_{1}}{\partial y}\right)^{2}+\left(\frac{\partial v_{2}}{\partial x}\right)^{2}+\left(\frac{\partial v_{2}}{\partial y}\right)^{2}\right)\,dxdy\]

Le champ de vitesse solution minimise ce Lagrangien \(\mathcal{L}(v_{1},v_{2})\), qui n’est autre que l’énergie dissipée sous forme visqueuse. La solution du problème de Stokes (3.15) est donc le champ de vitesse incompressible vérifiant les conditions aux limites (3.16) qui minimise la dissipation visqueuse.

La formulation faible correspond alors aux équations de Lagrange:

\[\begin{split}\begin{aligned} <\frac{\partial\mathcal{L}}{\partial v_{1}}\,,\,\delta v_{1}> & = & 0\\ <\frac{\partial\mathcal{L}}{\partial v_{2}}\,,\,\delta v_{2}> & = & 0\end{aligned}\end{split}\]

3.3.2. Seconde formulation faible du problème de Stockes

Si on n’impose pas à la variation du champ de vitesse d’être incompressible, la formulation intégrale (3.18) contient un terme de pression \(p\). Il faut donc tenir compte d’une variation \(\delta p\) de ce champ de pression, qui doit être tel que le champ de vitesse \(\overrightarrow{\mathbf{V}}\) reste incompressible . Il faut donc multiplier l’équation (3.15) (qui est la condition d’incompressibilité \(div\,\overrightarrow{\mathbf{V}}=0\)) par \(\delta p\) et intégrer sur le domaine:

\[\int_{\Omega}\delta p\,div\,\overrightarrow{\mathbf{V}}\,dxdy=0\]

On remarque que c’est le terme symétrique de l’intégrale de pression dans (3.18), et qui traduit le fait que la puissance de toute variation de pression \(\delta p\)calculée pour le champ de vitesse \(\overrightarrow{\mathbf{V}}\) doit être nulle.

La formulation faible de (3.15)s’écrit donc

\[\begin{split}\left\{ \begin{array}{c} \mbox{Trouvez }(\overrightarrow{\mathbf{V}},p)\,\mbox{satisfaisant les CL {eq}`eq2.25`}\\ \int_{\Omega}\frac{\mu}{\rho}\,\overrightarrow{\mathbf{grad}}\,\overrightarrow{\mathbf{V}}\otimes\overrightarrow{\mathbf{grad}}\,\delta\overrightarrow{\mathbf{V}}\,dxdy=\int_{\Omega}p\,div\left(\delta\overrightarrow{\mathbf{V}}\right)\,dxdy\\ \int_{\Omega}\delta p\,div\,\overrightarrow{\mathbf{V}}\,dxdy=0\,\:\forall\delta\overrightarrow{\mathbf{V}},\delta p\,\mbox{ verifiant CL {eq}`2.24`} \end{array}\right.\end{split}\]

Cette formulation correspond aussi à un problème variationnel dont le Lagrangien s’écrit:

\[\begin{split}\begin{aligned} \mathcal{L}(v_{1},v_{2},p) & = & \frac{1}{2}\int_{\Omega}\frac{\mu}{\rho}\,\left(\left(\frac{\partial v_{1}}{\partial x}\right)^{2}+\left(\frac{\partial v_{1}}{\partial y}\right)^{2}+\left(\frac{\partial v_{2}}{\partial x}\right)^{2}+\left(\frac{\partial v_{2}}{\partial y}\right)^{2}\right)\,dxdy\\ & - & \int_{\Omega}p\left(\frac{\partial v_{1}}{\partial x}+\frac{\partial v_{2}}{\partial y}\right)dxdy\end{aligned}\end{split}\]

et les équations de Lagrange:

\[\begin{split}\begin{aligned} <\frac{\partial\mathcal{L}}{\partial v_{1}}\,,\,\delta v_{1}> & = & 0\\ <\frac{\partial\mathcal{L}}{\partial v_{2}}\,,\,\delta v_{2}> & = & 0\\ <\frac{\partial\mathcal{L}}{\partial p}\,,\,\delta p> & = & 0\end{aligned}\end{split}\]

Dans le Lagrangien, on remarque que la contrainte \(div\overrightarrow{\,\mathbf{V}}=0\) est multipliée par la pression. La pression apparaît donc comme le multiplicateur de Lagrange de la contrainte d’incompressibilité.

Dans la pratique, nous utiliserons plutôt la seconde formulation dans laquelle la contrainte est imposée explicitement à travers la pression, car elle est en générale plus simple à approximer numériquement. Cependant certaines méthodes numériques utilisent la première formulation.

3.3.3. Problème instationnaire

Pour le problème de Navier-Stockes avec des termes instationnaires, on applique le principe des puissances virtuelles pour obtenir la formulation faible des équations. Par contre, cette formulation n’est plus associée à une formulation variationnelle, puisque que l’on ne peut pas définir de Lagrangien.

3.4. Formulation faible: approche mathématique

Nous avons vu dans les exemples précédents que la formulation faible peut être obtenue à partir de principes mécaniques (principe des travaux virtuels, principe des puissances virtuelles), d’une formulation lagrangienne (pour des systèmes conservatifs). En fait cette formulation faible peut s’appliquer à n’importe quel système d’équations aux dérivées partielles en utilisant une généralisation de l’approche qui utilise l’analyse fonctionnelle.

C’est cette approche que nous présentons sur l’exemple de l’équation de la chaleur stationnaire avec un second membre \(f(x)\):

(3.20)\[-\frac{\partial^{2}u}{\partial x^{2}}=f\,\mbox{ dans }\Omega=[0,1]\]

et les conditions aux limites:

(3.21)\[u(0)=0,\,\,u(1)=0\]

La démarche est la suivante:

1. On multiplie l’équation (3.20) par une fonction test de \(x\) quelconque (variation de \(u(x)\)) \(v(x)\), et on intègre sur le domaine. Il vient:

   \[-\int_{0}^{1}\frac{\partial^{2}u}{\partial x^{2}}\,v\,dx=\int_{0}^{1}f.v\,dx\]

2. On intègre par partie le terme de plus haut degré en utilisant une formule de green:

   \[\int_{0}^{1}\frac{\partial u}{\partial x}\frac{\partial v}{\partial x}\,dx-\left[\frac{\partial u}{\partial x}v\right]_{0}^{1}=\int_{0}^{1}f.v\,dx\]

   l’objectif de cette intégration par partie est de symétriser le problème et de faire apparaître une intégrale de bord pouvant être calculé à l’aide des conditions aux limites

3. On calcul l’intégrale de bord à l’aide des conditions aux limites. Pour les conditions de Dirichlet, on impose la valeur de la fonction, donc on impose à la fonction test (qui est variation) de s’annuler. Pour les conditions de Neumann, la condition aux limites permet le calcul du terme de bord si le problème est bien posé. On a donc avec (3.21):

   \[v(0)=0\,\,\mbox{ et }v(1)=0\]

   ce qui permet de calculer le terme de bord:

   \[\left[\frac{\partial u}{\partial x}v\right]_{0}^{1}=0-0=0\]

4. On obtient alors la formulation faible:

   \[\int_{0}^{1}\frac{\partial u}{\partial x}\frac{\partial v}{\partial x}\,dx=\int_{0}^{1}f.v\,dx\]

   qui doit être vérifiée quelque soit la fonction test \(v(x)\) vérifiant la condition imposée:

   \[v(0)=0,\,\,v(1)=0\]

5. On regarde quelles sont les conditions à imposées sur la fonction \(u(x)\)et les fonctions tests \(v(x)\)pour que cette formulation ait un sens:

• la fonction \(u(x)\) doit vérifier \(u(0)=0,\,\,u(1)=0\) et posséder une dérivée première de carré sommable en espace (i.e. telle que les intégrales puissent être calculées dans la formulation faible).

• la fonction test \(v(x)\) doit vérifiée \(v(0)=0,\,\,v(1)=0\) et posséder une dérivée première de carré sommable.

D’un point de vue mathématique, les fonctions \(f(x)\) de carré sommable (i.e. telle que \(\int_{\Omega}f(x)^{2}dx\) existe) forment un espace vectoriel de Hilbert noté \(\mathcal{L}^{2}(\Omega)\). Cet espace contient l’espace des fonctions continues \(\mathcal{C}^{0}(\Omega)\), mais est bien plus vaste: une fonction continue par morceaux appartiens à \(\mathcal{L}^{2}(\Omega)\), mais pas à \(\mathcal{C}^{0}(\Omega)\). Cet espace vectoriel est doté d’un produit scalaire, noté \(<,>\)

(3.22)\[\left\langle f,g\right\rangle =\int_{\Omega}f(x)g(x)\,dx\]

De même les fonctions, dont la dérivée est de carré sommable, forment un espace vectoriel de Hilbert \(\mathcal{H}^{1}(\Omega)\). Cet espace contiens l’espace des fonctions à dérivées continues \(\mathcal{C}^{1}(\Omega)\), mais est bien plus vaste.

La formulation faible s’écrit alors:

\[\mbox{Trouvez }u(x)\in H^{1}(\Omega)\,\mbox{ t.q. }u(0)=0,\,\,u(1)=0\]

(3.23)\[\begin{aligned} \int_{\Omega}\frac{\partial u}{\partial x}\frac{\partial v}{\partial x}\,dx=\int_{\Omega}f.v\,dx & & \forall v\in H^{1}(\Omega)\mbox{ t.q. }v(0)=0,v(1)=0\end{aligned}\]

D’un point de vue mathématique et numérique, cette formulation (3.23) a de nombreux avantages par rapport à l’équation aux dérivées partielles (3.20). En particulier les conditions de régularité imposées sur la solution moins contraignantes dans (3.23) avec une solution dans \(H^{1}(\Omega)\), que dans (3.20) avec une solution dans \(\mathcal{C}^{2}(\Omega)\). Cela permet d’une part de calculer des solutions généralisées (i.e. qui ne sont pas dans \(\mathcal{C}^{2}(\Omega)\)), et d’autre part la construction plus simple d’approximations de la solution (qui seront dans \(H^{1}(\Omega)\) même si la solution est dans \(\mathcal{C}^{2}(\Omega)\)).

Cette formulation faible a été obtenue par une généralisation du principe des travaux ou puissances virtuelles. En notant \(H_{0}^{1}(\Omega)\) l’espace des fonctions \(v\) de \(H^{1}(\Omega)\) telles que \(v(0)=0,\,v(1)=0\), elle s’écrit:

\[\begin{split}\left\{ \begin{array}{c} \mbox{Trouvez }u(x)\in H_{0}^{1}(\Omega)\\ \int_{\Omega}\frac{\partial u}{\partial x}\frac{\partial v}{\partial x}\,dx=\int_{\Omega}f\,v\,dx\,\,\forall v(x)\in H_{0}^{1}(\Omega) \end{array}\right.\end{split}\]

soit en utilisant le produit scalaire (3.22)

\[\begin{split}\left\{ \begin{array}{c} \mbox{Trouvez }u(x)\in H_{0}^{1}(\Omega)\\ \left\langle \frac{\partial u}{\partial x},\frac{\partial v}{\partial x}\right\rangle =\left\langle f,v\right\rangle \,\,\forall v(x)\in H_{0}^{1}(\Omega) \end{array}\right.\end{split}\]

On peut donner une interprétation de cette formulation. Notons symboliquement l’équation aux dérivée partielle (3.20) (associée aux conditions aux limites (3.21)):

\[L\,u=f\]

Le résidu de cette équation s’écrit pour une fonction \(w\):

\[R(w)=L\,w\,-f\]

La formulation faible consiste à écrire que pour la solution \(u\), le résidu \(R(u)\) doit être orthogonal au sens du produit scalaire (3.22) à l’espace des fonctions tests \(v\)

\[\left\langle R(u),v\right\rangle =0\,\,\forall v\in H_{0}^{1}(\Omega)\]

En intégrant par partie, on symétrise ce produit scalaire, pour obtenir une forme bilinéaire \(a(u,v)=\left\langle \frac{\partial u}{\partial x},\frac{\partial v}{\partial x}\right\rangle\). L’équation finale s’écrit donc

\[a(u,v)=\left\langle f,v\right\rangle \,\,\forall v\in H_{0}^{1}(\Omega)\label{chap2:eq36}\]

Un théorème mathématique (Lax Milgram) permet alors de montrer l’unicité de la solution \(u(x)\) , qui est la projection dans \(H_{0}^{1}(\Omega)\) de la forme linéaire \(l(v)=\left\langle f,v\right\rangle\).

Si la forme bilinéaire \(a(u,v)\) est symétrique et V-elliptique (i.e. définie positive), cette forme bilinéaire est un produit scalaire dans \(H_{0}^{1}(\Omega)\), et le problème correspond à un problème de minimisation d’une fonctionnelle \(\mathcal{J}(w)\) dans \(H_{0}^{1}(\Omega)\). Pour notre problème:

\[a(u,v)=\left\langle \frac{\partial u}{\partial x},\frac{\partial v}{\partial x}\right\rangle =\left\langle u,v\right\rangle _{H_{0}^{1}}\]

et la fonctionnelle \(\mathcal{J}(w)\) s’écrit:

\[\mathcal{J}(w)=\frac{1}{2}a(w,w)-l(w)=\frac{1}{2}\left\langle w,w\right\rangle _{H_{0}^{1}}-\left\langle f,w\right\rangle\]

Cette fonctionnelle est bien minimale en \(u\). En effet, en posant \(v=w-u\)

\[\begin{split}\begin{aligned} \mathcal{J}(w) & = & \mathcal{J}(u+v)\\ & = & \frac{1}{2}\left\langle u,u\right\rangle _{H_{0}^{1}}+<u,v>_{H_{0}^{1}}+\frac{1}{2}<v,v>_{H_{0}^{1}}-\left\langle f,u\right\rangle -\left\langle f,v\right\rangle \\ & = & J(u)+\frac{1}{2}<v,v>_{H_{0}^{1}}+<u,v>_{H_{0}^{1}}-\left\langle f,v\right\rangle \end{aligned}\end{split}\]

et en utilisant (3.22), il vient

\[\mathcal{J}(w)=J(u)+\frac{1}{2}<v,v>_{H_{0}^{1}}\le J(u)\,\,\,\forall w\in H_{0}^{1}\]

Cette fonctionnelle \(J(u)\) est le Lagrangien du système (au signe près) , et on retrouve la formulation variationnelle:

\[\begin{split}\left\{ \begin{array}{c} \mbox{Trouvez }\,u(x)\in H_{0}^{1}\,\mbox{t.q}\\ \mathcal{J}(u)\le\mathcal{J}(w)\,\,\forall w\in H_{0}^{1} \end{array}\right.\label{chap2:eq37}\end{split}\]

\[\mbox{avec }\mathcal{J}(w)=\frac{1}{2}a(w,w)-l(w)=\frac{1}{2}\int_{\Omega}\left(\frac{\partial w}{\partial x}\right)^{2}\,dx-\int_{\Omega}f.w\,dx\]

Pour ce problème, on peut calculer la valeur de la fonctionnelle \(J(u)\) à l’équilibre, en choisissant comme fonction test \(v(x)\) la solution \(u(x)\) dans la formulation faible.

\[a(u,u)=l(u)\]

d’où

\[\mathcal{J}(u)=\frac{1}{2}a(u,u)-l(u)=-\frac{1}{2}a(u,u)\]

3.5. Formulation faible discrète

Nous avons vue qu’il existait plusieurs approches (travaux virtuels, Lagrange, approche formelle) pour obtenir la formulation faible d’une équation (ou système d’équations) aux dérivées partielles \(Lu=f\).

Cette formulation faible peut s’écrire sous la forme symbolique:

(3.24)\[\begin{split}\left\{ \begin{array}{c} \mbox{Trouvez }u\in V\\ a(u,v)=l(v)\,\,\forall v\in V \end{array}\right.\end{split}\]

où \(V\) est l’espace des solutions, \(a(u,v)\) la forme bilinéaire associée aux dérivées partielles de l’équation et \(l(v)\) la forme linéaire associée au second membre.

L’espace des solutions \(V\) est un espace de fonctions (de dimension infinie), et la recherche d’une solution analytique de (3.24) dans cet espace n’est en générale pas possible.

On recherche donc une solution approchée \(u^{h}\), en construisant une approximation \(V^{h}\) de dimension finie \(N\) de l’espace des solutions \(V\). On se donne pour cela une famille libre de \(N\) fonctions \(\left\{ \Phi_{i}\right\} _{i=1,N}\) de \(V\), et on construit l’espace vectoriel \(V^{h}\) engendré par ces \(N\) fonctions:

\[V^{h}=\left\{ v^{h}/v^{h}=\sum_{i=1}^{N}v_{i}\Phi_{i}\right\} \subset V\]

On cherche alors la solution de la formulation dans cette espace \(V^{h}\), en résolvant le problème discret:

\[\begin{split}\left\{ \begin{array}{c} \mbox{Trouvez }u^{h}\in V^{h}\\ a(u^{h},v^{h})=l(v^{h})\,\,\forall v^{h}\in V^{h} \end{array}\right.\end{split}\]

En décomposant la solution \(u^{h}\) sur la base des fonctions \(\Phi_{j}\)

\[u^{h}=\sum_{j=1}^{N}u_{j}\Phi_{j}\]

et en prenant comme fonction test \(v^{h}\) chacune des fonctions de base \(\Phi_{i}\) (ce qui est équivalent), la formulation faible s’écrit, en tenant de la bilinéarité de \(a(u,v)\)

\[\sum_{j=1}^{N}a(\Phi_{j},\Phi_{i})\,u_{j}=l(\Phi_{i})\,\,\,\mbox{pour }i=1,N\]

qui n’est autre qu’un système linéaire d’ordre \(N\)

(3.25)\[\mathbf{A}U=B\,\,\mbox{avec } \mathbf{A}_{ij}=a(\Phi_{j},\Phi_{i})\,,\,U=\left\{ u_{i}\right\} ,\,B=\left\{ l(\Phi_{i})\right\}\]

qu’il suffit de résoudre pour obtenir la solution approchée \(u^{h}\).

Si le problème admet une formulation variationnelle, la solution \(u^{h}\) minimise la fonctionnelle \(J(v^{h})\) dans \(V^{h}\):

\[\begin{split}\begin{aligned} J(u^{h}) & = & \frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}u_{i}a(\Phi_{j},\Phi_{i})u_{j}-\sum_{i=1}^{N}u_{i}l(\Phi_{i})\\ & = & \frac{1}{2}U^{t}\mathbf{A}U-UB^{t}\end{aligned}\end{split}\]

\(J(u^{h})\) est une fonction quadratique de \(N\) variables \(\left\{ u_{i}\right\}\) , qui est minimum si le gradient de \(J(u_{1},u_{2},..u_{N})\) par rapport à ces \(N\) variables est nul.

Or

\[\frac{\partial J}{\partial u_{i}}=\sum_{j=1}^{N}\mathbf{A}_{ij}U_{j}-B_{i}\]

et la condition de minimisation conduit alors au système linéaire (3.25).

La méthode des éléments finis n’est qu’une méthode particulière pour construire l’espace \(V^{h}\) et les fonctions de base \(\Phi_{i}\).

Pour terminer, nous allons donner quelques propriétés de la formulation faible discrète.

Formulation faible discrète

Propriétés mathématiques de la formulation faible discrète

1. cette formulation traduit l’orthogonalité du résidu de l’équation par rapport à l’espace des fonctions tests:

   \[a(u^{h},v^{h})-l(v^{h})=\left\langle Lu^{h}-f,v^{h}\right\rangle =0\,\,\forall v^{h}\in V^{h}\]

2. si \(a(\,,\,)\) est un produit scalaire dans \(V\), alors la solution approchée \(u^{h}\) est la projection de la solution exacte \(u\) dans \(V^{h}\), i.e. l’erreur \(u-u^{h}\) est perpendiculaire à \(V^{h}\)[4]:

   \[a(u-u^{h},v^{h})=\left\langle u-u^{h},v^{h}\right\rangle _{V}=0\,\,\,\forall v^{h}\in V\]

3. \(u^{h}\)est alors la meilleur approximation de \(u\) dans \(V^{h}\), puisque la norme de l’erreur \(u-u^{h}\)est minimum

   \[a(u-u^{h},u-u^{h})=\left\Vert u-u^{h}\right\Vert _{V}^{2}\le\left\Vert u-v^{h}\right\Vert _{V}^{2}\,\,\,\forall v^{h}\in V^{h}\]

   (pour le montrer on calcul \(a(u-v^{h},u-v^{h})\) avec \(v^{h}=u^{h}+w^{h}\))

4. on en déduit que l’approximation \(u^{h}\) est au moins aussi bonne que l’interpolation \(u^{I}\) de \(u\) dans \(V^{h}\) (obtenue en associant \(N\) points d’interpolation \(P_{i}\) aux \(N\) fonctions de base \(\Phi_{i}\)):

   \[u^{I}=\sum_{i=1}^{N}u(P_{i})\,\Phi_{i}\]

   i.e. l’erreur d’approximation \(\left\Vert u-u^{h}\right\Vert _{V}^{2}\) est majorée par l’erreur d’interpolation \(\left\Vert u-u^{I}\right\Vert _{V}^{2}\)

3.5.1. Traitement d’un exemple

Considérons le problème (3.20),(3.21) avec \(f=1\).La solution analytique \(u_{ex}\) est le polynôme du second degré:

\[u_{ex}(x)=\frac{1}{2}\,x*(1-x)\]

La fonctionnelle \(\mathcal{J}(u)\) de la formulation variationnelle s’écrit:

\[\mathcal{J}(u)=\frac{1}{2}\int_{0}^{1}\left(\frac{\partial u}{\partial x}\right)^{2}dx-\int_{0}^{1}u\,dx\]

et un calcul directe fournit:

(3.26)\[\mathcal{J}(u_{ex})=-\frac{1}{24}\simeq-0.04167\]

Nous allons calculer une approximation de cette solution exacte sur une base de fonctions trigonométriques. Compte tenu des conditions aux limites et des propriétés de symétrie du problème par rapport à \(x=1/2\), les fonctions choisies sont les fonctions de base \(\Phi_{i}\) :

\[\Phi_{i}(x)=\sin\,\left((2i-1)\pi\,x\right)\]

Et nous allons calculer la solution approchée \(u^{h}\) en utilisant que deux fonctions de base \(\Phi_{1}\) et \(\Phi_{2}\)

\[u^{h}(x)=a_{1}\Phi_{1}(x)+a_{2}\Phi_{2}(x)\]

On peut alors calculer \(\mathcal{J}(u^{h})\) analytiquement

\[\mathcal{J}(u^{h})=\frac{1}{4}\,\pi^{2}a_{1}^{2}+\frac{9}{4}\,\pi^{2}a_{2}^{2}-\frac{2}{3}\,\frac{3a_{1}+a_{2}}{\pi}\]

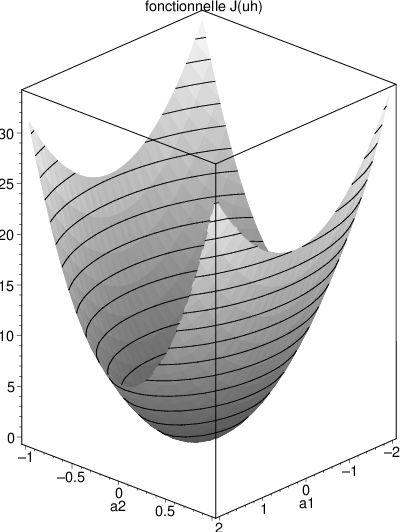
Fig. 3.3 fonctionnelle \(J(u^{h})\)

Cette fonctionnelle est un paraboloïde de révolution (représenté sur la figure ci-dessus), dont le minimum est obtenu par résolution du système d’équations:

\[\frac{\partial\mathcal{J}(u^{h})}{\partial a_{1}}=0,\,\,\frac{\partial\mathcal{J}(u^{h})}{\partial a_{2}}=0\]

Ces équations s’écrivent:

\[\frac{\pi^{2}}{2}a_{1}-\frac{2}{\pi}=0,\,\,\frac{9\pi^{2}}{2}a_{2}-\frac{2}{3\pi}=0\]

Ces équations sont identiques à celles obtenues avec la formulation faible (3.23), en remplaçant la solution exacte \(u\) par son approximation \(u^{h}\), et les fonctions tests \(v\) par les fonctions de base \(\Phi_{1}\) et \(\Phi_{2}\)[5]. Ce système d’équations linéaires permet de déterminer les coefficients inconnus \(\left\{ a_{i}\right\}\) .

La solution approchée \(u^{h}\) s’écrit:

\[u^{h}(x)=\frac{4}{\pi^{3}}\sin(\pi x)+\frac{4}{27\pi^{3}}\sin(3\pi x)\]

Fig. 3.4 solution approchée \(u^{h}\)

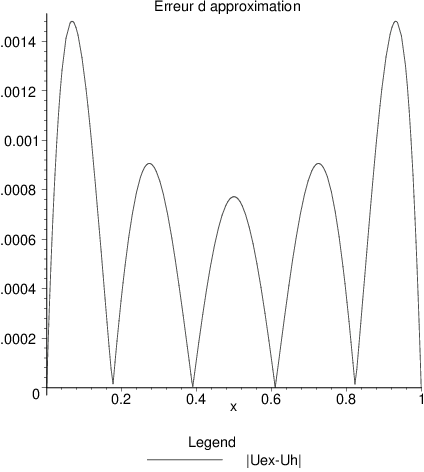
Fig. 3.5 erreur d’approximation \(|u_{ex}-u^{h}|\)

On a tracé sur ces figures la solution approchée \(u^{h}\) comparée à la solution exacte \(u_{ex}\) , ainsi que l’erreur d’approximation \(|u_{ex}-u^{h}|\). On constate sur la figure que l’on a une très bonne approximation de la solution, avec une erreur uniformément répartie (de l’ordre de \(1\%\) maximum).

Pour cette solution approchée \(u^{h}\), la valeur de la fonctionnelle \(\mathcal{J}(u^{h})\) vaut:

\[\mathcal{J}(u^{h})=-\frac{328}{81\pi^{4}}\simeq-0.04157\]

qui est légèrement plus grande que la valeur exacte (3.26).

Nous allons maintenant montrer que la solution approchée \(u^{h}\) calculée avec la formulation faible discrète est la meilleure approximation[6] de la solution exacte \(u_{ex}\) du problème dans l’espace d’approximation \(V^{h}\) engendré par les fonctions de base \(\Phi_{1}\) et \(\Phi_{2}\).

Pour cela nous allons tout d’abord comparer \(u^{h}\) à l’interpolation \(u_{I}\) dans \(V^{h}\)de la solution exacte \(u_{ex}\) aux 5 points d’interpolation \(X=\left\{ 0,\frac{1}{4},\frac{1}{2},\frac{3}{4},1\right\}\). Cette interpolation de \(u_{ex}\) s’écrit:

\[u_{I}(x)=b_{1}\Phi_{1}(x)+b_{2}\Phi_{2}(x)\]

et coïncide avec la solution exacte aux points d’interpolation \(X_{i}\):

\[\begin{aligned} u_{I}(X_{i}) & = & u_{ex}(X_{i})\,\,i=1,5\end{aligned}\]

Compte tenu des propriétés de symétrie du problème, ces 5 relations ne donnent que 2 équations indépendantes;

\[\frac{\sqrt{2}}{2}b_{1}+\frac{\sqrt{2}}{2}b_{2}=\frac{3}{32}\,\,\,\,,\,\,\,\,b_{1}-b_{2}=\frac{1}{8}\]

qui permettent la détermination unique des coefficients \(b_{1}\) et \(b_{2}\). L’interpolation \(u_{I}\) s’écrit donc:

\[u_{I}(x)=\left(\frac{3\sqrt{2}}{64}+\frac{1}{16}\right)\Phi_{1}(x)+\left(\frac{3\sqrt{2}}{64}-\frac{1}{16}\right)\Phi_{2}(x)\]

Cette solution approxime bien la solution exacte \(u_{ex}\), comme on peut le constater sur la figure ci-dessous, mais l’erreur d’interpolation est plus grande en moyenne que l’erreur d’approximation comme on le constate sur cette même figure.

Fig. 3.6 solution interpolée \(u_{I}\)

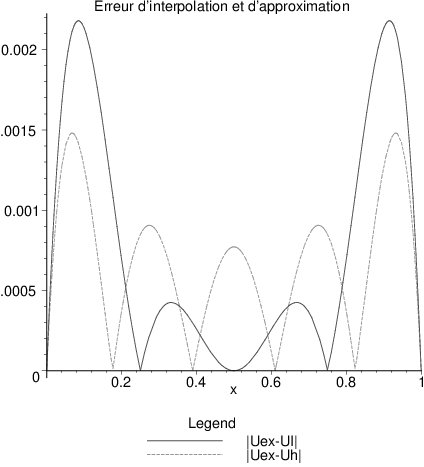
Fig. 3.7 erreur d’interpolation \(|u_{ex}-u_{I}|\)

Pour le vérifier, on calcule l’erreur moyenne (en norme \(\mathcal{L}^{2}\)):

\[\int_{0}^{1}(u_{I}-u_{ex})^{2}\,dx\simeq0.1137\,10^{-5}\,\,\,,\,\,\,\,\int_{0}^{1}(u^{h}-u_{ex})^{2}\,dx\simeq0.0627\,10^{-5}\]

et constate donc que l’erreur d’approximation est plus faible que l’erreur d’interpolation, et donc la solution \(u^{h}\) est meilleure que l’interpolation \(u_{I}\).

De façon plus générale, si l’on cherche la fonction \(v^{h}\) de \(V^{h}\) qui minimise l’erreur d’approximation (au sens de la norme \(\mathcal{L}^{2}\)):

\[err=\int_{0}^{1}(v^{h}-u_{ex})^{2}\,dx\]

on retrouve l’approximation \(u^{h}\).

De même, si l’on cherche la fonction \(v^{h}\) de \(V^{h}\) qui minimise l’erreur d’approximation (au sens de la norme associée à la fonctionnelle \(\mathcal{J}\))

\[err=\int_{\Omega}\left(\frac{\partial}{\partial x}(v^{h}-u_{ex})\right)^{2}\,dx\]

on retrouve encore l’approximation \(u^{h}\). En fait la minimisation de cette erreur conduit à la formulation faible discrète, d’où le résultat.

---

[1]

si \(J(u)\) est minimum, alors \(-J(u)\) est maximum, et vice et versa

[3]

conditions aux limites de Neumann (force imposée)

[4]

puisque \(a(u,v^{h})=l(v^{h})\) et \(a(u^{h},v^{h})=l(v^{h})\) \(\forall v^{h}\in V^{h}\), et \(V^{h}\subset\)V

[5]

les variations \(\delta u^{h}\) sont des combinaisons linéaires des fonctions de base

[6]

au sens de la norme \(\mathcal{L}^{2}(\Omega)\)