Les équations de la mécanique numérique

2. Les équations de la mécanique numérique#

2.1. Équation de bilan pour un champ scalaire#

En mécanique des milieux continus, l’équation d’évolution d’une quantité physique \(W(t,x,y,z)\) par unité de masse (température, concentration, énergie …) traduit un principe de conservation, et donc un bilan effectué sur un petit élément de volume \(dV=dxdydz\) fixe par rapport à l’observateur (formulation eulérienne).

En notant \(\rho\), la masse volumique du milieu, la quantité de \(W\) dans l’élément \(dV\) est \(\rho WdV\). La variation temporelle de \(W\) est donc égale à la somme des flux de \(W\) à travers les facettes \(dS\) à laquelle on ajoute les termes sources volumiques \(T_{s}\).

L’équation de bilan peut s’écrire sous forme générique:

(2.1)#\[ \underbrace{\frac{\partial}{\partial t}(\rho W)dV}_{\mbox{variation temporelle}}=\sum_{\mbox{facette}}\underbrace{\left(\phi_{c}dS+\phi_{d}dS\right)}_{\mbox{flux}}+\underbrace{T_{s}dV}_{\mbox{source}} \]

Cette équation contient

  1. un terme instationnaire \(\frac{\partial\rho W}{\partial t}\),

  2. des termes de flux surfaciques \(\phi\), traduisant un bilan à travers les surfaces \(dS\) du volume \(dV\),

  3. des termes sources volumiques \(T_{s}\).

Pour les flux, on distingue des flux par diffusion moléculaire \(\phi_{d}\), qui sont proportionnels au gradient de \(W\) dans la direction normale à la facette \(dS\):

\[\phi_{d}=\lambda\frac{\partial W}{\partial n}\mbox{ loi de Fourier,}\]

et des flux de convection \(\phi_{c}\), qui traduisent le transport de \(W\) par le milieu et sont proportionnels à la vitesse \(\overrightarrow{\mathbf{V}}\) dans la direction normale à la facette \(dS\):

\[\phi_{c}=\rho W\,\overrightarrow{\mathbf{V}}.\overrightarrow{n}\]

En considérant un milieu homogène suivant l’axe \(z\) , avec un champ de vitesse bidimensionnel \(\overrightarrow{V}=(v_{1},v_{2})\) (figure ci-dessous)

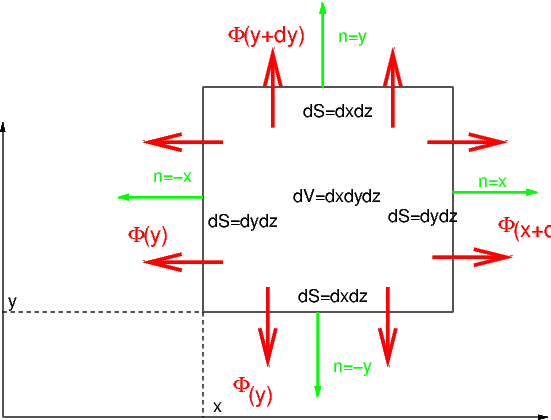
../_images/bilan.png

Fig. 2.1 Bilan de flux sur un élément de volume(en 2D)#

le bilan précédent (2.1) s’écrit:

\[\begin{split}\begin{aligned} \frac{\partial\rho W}{\partial t}dxdydz & = & \left(\left(\lambda\frac{\partial W}{\partial x}\right)_{x+dx}-\left(\lambda\frac{\partial W}{\partial x}\right)_{x}\right)dydz+\left(-\left(v_{1}\rho W\right)_{x+dx}+\left(v_{1}\rho W\right)_{x}\right)dydz\\ & + & \left(\left(\lambda\frac{\partial W}{\partial y}\right)_{y+dy}-\left(\lambda\frac{\partial W}{\partial x}\right)_{y}\right)dxdz+\left(-\left(v_{2}\rho W\right)_{y+dy}+\left(v_{2}\rho W\right)_{y}\right)dxdz\\ & + & T_{s}(W)dxdydz\end{aligned}\end{split}\]

En effectuant les développements limités des termes en \(x+dx\) et \(y+dy\) et un passage à la limite, on obtient l’équation classique de bilan pour un scalaire \(W\):

\[\begin{split}\begin{aligned} \frac{\partial\rho W}{\partial t} & = & \frac{\partial}{\partial x}(\lambda\frac{\partial W}{\partial x})+\frac{\partial}{\partial y}(\lambda\frac{\partial W}{\partial y})-\frac{\partial}{\partial x}(\rho v_{1}W)-\frac{\partial}{\partial y}(\rho v_{2}W)+T_{s}(W)\\ & = & div(\lambda\,\overrightarrow{grad\,}W)-div(\overrightarrow{\mathbf{V}}\rho W)+T_{s}(W)\end{aligned}\end{split}\]

Cette équation est l’équation classique de convection diffusion. A partir de cette équation, on retrouve les équations classiques en mécanique des milieux continus:

  1. équation de diffusion pure:

    (2.2)#\[div(\lambda\,\overrightarrow{grad}W)=0\]

    l’exemple type est l’équation de la chaleur stationnaire, qui donne la répartition stationnaire de la température dans un solide homogène:

    (2.3)#\[\Delta T=\frac{\partial^{2}T}{\partial x^{2}}+\frac{\partial^{2}T}{\partial y^{2}}=0\]

  2. équation de diffusion instationnaire:

    (2.4)#\[\frac{\partial\rho W}{\partial t}=div(\lambda\,\overrightarrow{grad}W)\]

    l’exemple type est l’équation de la chaleur instationnaire, qui traduit l’évolution temporelle de la température dans un solide homogène:

    (2.5)#\[\frac{\partial T}{\partial t}=K\Delta T=K(\frac{\partial^{2}T}{\partial x^{2}}+\frac{\partial^{2}T}{\partial y^{2}})\]

  3. équation de convection pure:

    \[\frac{\partial\rho W}{\partial t}+div(\overrightarrow{\mathbf{V}}\rho W)=0\]

    l’exemple type est l’équation de transport, qui traduit le transport d’un scalaire \(C\) par le champ de vitesse d’un fluide incompressible (\(\rho=cste\), \(div\overrightarrow{\mathbf{V}}=0\)):

    \[\frac{\partial C}{\partial t}+\overrightarrow{\mathbf{V}}\,\overrightarrow{grad}C=0\]

  4. équation de diffusion convection:

    (2.6)#\[\frac{\partial\rho W}{\partial t}+div(\overrightarrow{\mathbf{V}}\rho W)=div(\lambda\,\overrightarrow{grad}W)\]

    l’exemple type est l’équation de convection diffusion de la température dans un fluide incompressible (\(\rho=cste\), \(div\overrightarrow{\mathbf{V}}=0\)):

(2.7)#\[\frac{\partial T}{\partial t}+\overrightarrow{\mathbf{V}}\,\overrightarrow{grad}\, T=K\Delta T\]

2.2. Équation de bilan pour un champ vectoriel#

Le principe fondamental de la dynamique, qui traduit l’équilibre entre l’accélération et les forces appliquées, conduit lorsqu’on l’applique à un élément de volume à une équation de bilan vectorielle. Cette équation de bilan a cependant une forme différente suivant la variable vectorielle choisie pour décrire le mouvement.

2.2.1. Équation de bilan local en mécanique des solides#

En mécanique des solides, la variable choisie est le champ de déplacement \(\overrightarrow{U}\). L’accélération d’un élément de volume de masse \(\rho dV\) , qui s’écrit \(\vec{\gamma}=\frac{\partial^{2}\vec{U}}{\partial t^{2}}\) , est égale à la somme des contraintes \(\overrightarrow{\sigma}.\overrightarrow{n}\) (avec une composante normale \(\sigma\) et une composante tangentielle \(\tau\)) qui s’exercent sur les facettes \(ds\), auquel on ajoute les forces volumiques \(\overrightarrow{f}\).

Cette équation de bilan s’écrit:

\[\rho\frac{\partial^{2}\overrightarrow{U}}{\partial t^{2}}dV=\sum_{\mbox{facettes}}\overrightarrow{\sigma}.\overrightarrow{n}\, dS\,+\overrightarrow{f}\, dV\]
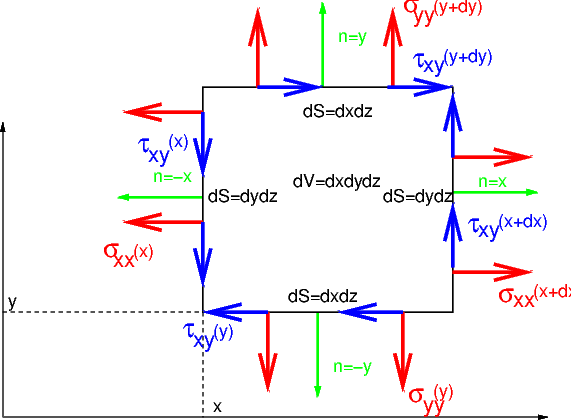
../_images/bilanF.png

Fig. 2.2 bilan des forces sur un élément de solide (en 2D)#

Pour un problème plan (figure ci-dessus), ce bilan s’écrit sous la forme de 2 équations scalaires:

\[\begin{split}\begin{aligned} \rho dxdydz\frac{\partial^{2}u_{1}}{\partial t^{2}} & = & \left(\sigma_{xx}(x+dx)-\sigma_{xx}(x)\right)dydz+\left(\tau_{xy}(y+dy)-\tau_{xy}(y)\right)dxdz+f_{1}dxdydz\\ \rho dxdydz\frac{\partial^{2}u_{2}}{\partial t^{2}} & = & \left(\sigma_{yy}(y+dy)-\sigma_{yy}(y)\right)dxdz+\left(\tau_{xy}(x+dx)-\tau_{xy}(x)\right)dydz+f_{2}dxdydz\end{aligned}\end{split}\]

En effectuant des développements limités et après une passage à la limite, on obtient les équations d’équilibre:

\[\begin{split}\begin{aligned} \rho\frac{\partial^{2}u_{1}}{\partial t^{2}} & = & \frac{\partial\sigma_{xx}}{\partial x}+\frac{\partial\tau_{xy}}{\partial y}+f_{1}\\ \rho\frac{\partial^{2}u_{2}}{\partial t^{2}} & = & \frac{\partial\tau_{xy}}{\partial x}+\frac{\partial\sigma_{yy}}{\partial y}+f_{2}\end{aligned}\end{split}\]

soit sous forme vectorielle:

\[\rho\frac{\partial^{2}\overrightarrow{\mathbf{U}}}{\partial t^{2}}=\overrightarrow{\mathbf{div}}\,\overrightarrow{\sigma}+\overrightarrow{f}\]

La loi de comportement du matériau permet d’obtenir la relation entre les contraintes \(\overrightarrow{\sigma}\) et les déformations \(\overrightarrow{\varepsilon}\). En élasticité linéaire, cette relation s’écrit:

\[\overrightarrow{\sigma}=\mathbf{D}\,\overrightarrow{\varepsilon}\]

où \(\mathbf{D}\) est la matrice des propriétés du matériau. Le tenseur des contraintes \(\overrightarrow{\sigma}\) et celui des déformations sont symétriques et s’écrivent:

\[\begin{split} \overrightarrow{\sigma} = \left[\begin{array}{ccc} \sigma_{xx} & \tau_{xy} & \tau_{zx} \\ \tau_{xy} & \sigma_{yy} & \tau_{yz} \\ \tau_{zx} & \tau_{yz} & \sigma_{zz} \\ \end{array}\right] \mbox{ et } \overrightarrow{\varepsilon} = \left[\begin{array}{ccc} \varepsilon_{xx} & \varepsilon_{xy} & \varepsilon_{zx} \\ \varepsilon_{xy} & \varepsilon_{yy} & \varepsilon_{yz} \\ \varepsilon_{zx} & \varepsilon_{yz} & \varepsilon_{zz} \\ \end{array}\right] \mbox{ et } \end{split}\]

La loi de Hooke pour un solide élastique isotrope s’écrit sous forme matricielle en notant \(E\) le coefficient d’élasticité et \(\nu\) le module d’Young du matériau:

\[ \overrightarrow{\sigma} = \frac{E}{1+\nu} \left(\overrightarrow{\varepsilon} + \frac{nu}{1-2\nu} Tr(\overrightarrow{\varepsilon}) \mathbf{Id} \right) \]

et sous forme vectorielle explicite:

\[\begin{split}\left[\begin{array}{c} \sigma_{xx}\\ \sigma_{yy}\\ \sigma_{zz}\\ \tau_{xy}\\ \tau_{yz}\\ \tau_{zx}\end{array}\right]=\frac{E}{(1+\nu)(1-2\nu)}\left[\begin{array}{cccccc} 1-\nu & \nu & \nu & 0 & 0 & 0\\ \nu & 1-\nu & \nu & 0 & 0 & 0\\ \nu & \nu & 1-\nu & 0 & 0 & 0\\ 0 & 0 & 0 & 1-2\nu & 0 & 0\\ 0 & 0 & 0 & 0 & 1-2\nu & 0\\ 0 & 0 & 0 & 0 & 0 & 1-2\nu\end{array}\right]\left[\begin{array}{c} \varepsilon_{xx}\\ \varepsilon_{yy}\\ \varepsilon_{zz}\\ \varepsilon_{xy}\\ \varepsilon_{yz}\\ \varepsilon_{zx}\end{array}\right]\end{split}\]

Dans le cas d’un champ de contrainte plane \((\sigma_{zz}=\tau_{yz}=\tau_{zx}=0)\), la relation se simplifie puisque \(\varepsilon_{zz}=-\frac{\nu}{1-\nu}(\varepsilon_{xx}+\varepsilon_{yy})\)

\[\begin{split}\begin{aligned} \left[\begin{array}{c} \sigma_{xx}\\ \sigma_{yy}\\ \tau_{xy}\end{array}\right] & = & \frac{E}{(1+\nu)(1-2\nu)}\left[\begin{array}{ccc} \frac{1-2\nu}{1-\nu} & \nu\frac{1-2\nu}{1-\nu} & 0\\ \nu\frac{1-2\nu}{1-\nu} & \frac{1-2\nu}{1-\nu} & 0\\ 0 & 0 & 1-2\nu\end{array}\right]\left[\begin{array}{c} \varepsilon_{xx}\\ \varepsilon_{yy}\\ \varepsilon_{xy}\end{array}\right]\\ & = & \frac{E}{1-\nu^{2}}\left[\begin{array}{ccc} 1 & \nu & 0\\ \nu & 1 & 0\\ 0 & 0 & 1-\nu\end{array}\right]\left[\begin{array}{c} \varepsilon_{xx}\\ \varepsilon_{yy}\\ \varepsilon_{xy}\end{array}\right]\end{aligned}\end{split}\]

Dans le cas d’un champ de contrainte unidimensionnel \((\sigma_{yy}=\tau_{xy}=0)\), on retrouve les relations classiques de la résistance des matériaux, en utilisant \(\varepsilon_{yy}=-\nu\,\varepsilon_{xx}\):

\[\sigma_{xx}=E\,\varepsilon_{xx}\]

La relation cinématique lie le champ de déformation \(\overrightarrow{\varepsilon}\) au champ de déplacement \(\overrightarrow{U}\):

\[\varepsilon_{xx}=\frac{\partial u_{1}}{\partial x}\,,\,\tau_{xy}=\frac{1}{2}(\frac{\partial u_{1}}{\partial y}+\frac{\partial u_{2}}{\partial x})\,,\,\varepsilon_{yy}=\frac{\partial u_{2}}{\partial y}\]

A partir de ces équations d’équilibres, on retrouve les équations classiques

  1. équation de traction en statique:

    qui traduit l’équilibre d’une poutre en traction-compression unidimensionnel

    (2.8)#\[E\frac{\partial u_{1}^{2}}{\partial x^{2}}=0\]

  2. équation de traction en dynamique:

    qui modélise les vibrations libres d’un poutre en traction-compression

    (2.9)#\[\rho\frac{\partial^{2}u_{1}}{\partial t^{2}}=E\frac{\partial u_{1}^{2}}{\partial x^{2}}\]

  3. équations couplées en statique:

    qui traduisent l’équilibre d’une plaque en traction

    (2.10)#\[\begin{split}\begin{aligned} \frac{E}{1-\nu^{2}}\left(\frac{\partial}{\partial x}\left(\frac{\partial u_{1}}{\partial x}+\nu\frac{\partial u_{2}}{\partial y}\right)+\frac{\partial}{\partial y}\left(\frac{1-v}{2}\left(\frac{\partial u_{1}}{\partial y}+\frac{\partial u_{2}}{\partial x}\right)\right)\right) & = & 0\\ \frac{E}{1-\nu^{2}}\left(\frac{\partial}{\partial y}\left(\frac{\partial u_{2}}{\partial y}+\nu\frac{\partial u_{1}}{\partial x}\right)+\frac{\partial}{\partial x}\left(\frac{1-v}{2}\left(\frac{\partial u_{1}}{\partial y}+\frac{\partial u_{2}}{\partial x}\right)\right)\right) & = & 0 \end{aligned}\end{split}\]

  4. équations couplées en dynamique:

    qui modélisent les vibrations libres d’une plaque en traction-compression

    (2.11)#\[\begin{split}\begin{aligned} \rho\frac{\partial^{2}u_{1}}{\partial t^{2}} & = & \frac{E}{1-\nu^{2}}\,\frac{\partial}{\partial x}\left(\frac{\partial u_{1}}{\partial x}+\nu\frac{\partial u_{2}}{\partial y})\right)\\ & + & \frac{E}{2(1+\nu)}\,\frac{\partial}{\partial y}\left(\frac{\partial u_{1}}{\partial y}+\frac{\partial u_{2}}{\partial x}\right)\\ \rho\frac{\partial^{2}u_{2}}{\partial t^{2}} & = & \frac{E}{1-\nu^{2}}\,\frac{\partial}{\partial y}\left(\frac{\partial u_{2}}{\partial y}+\nu\frac{\partial u_{1}}{\partial x})\right) \\ & + & \frac{E}{2(1+\nu)}\,\frac{\partial}{\partial x}\left(\frac{\partial u_{1}}{\partial y}+\frac{\partial u_{2}}{\partial x}\right)\end{aligned}\end{split}\]

2.2.2. Équations de bilan moyennées en mécanique des solides#

Pour un certain nombre de problèmes de mécanique des solides, on peut simplifier l’approche locale précédente en moyennant les efforts sur un volume moyen, par exemple une section de poutre.

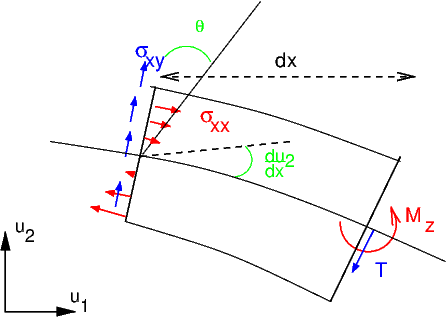
../_images/poutre.png

Fig. 2.3 poutre en flexion#

Ainsi pour une poutre en flexion, on peut utiliser les hypothèses de Bernoulli (les sections restent planes, orthogonales à la ligne moyenne et conservent leur forme). Dans une section \(S\) la résultante des efforts se réduit alors à une force de cisaillement \(T\) et un moment fléchissant \(M_{z}\):

\[T=\int_{S}\sigma_{xy}dS\,\,\mbox{ et }\,\,\, M_{z}=\int_{S}y\sigma_{xx}dS\]

L’équilibre des forces sur le volume entre 2 sections soumis à une charge linéique \(p\) (suivant y) s’écrit:

\[M_{z}(x+dx)=M_{z}(x)+Tdx\,\,\mbox{ et }\,\, T(x+dx)=T(x)+pdx\]

soit par passage à la limite:

\[\frac{dM_{z}}{dx}=T,\,\,\,\frac{dT}{dx}=p\]

ce qui fournit l’équation d’équilibre:

(2.12)#\[\frac{dM_{z}^{2}}{dx^{2}}=p \]

Puisque les sections ne subissent qu’une rotation (et pas de déformation), on peut exprimer les déplacements en fonction de l’angle de rotation \(\theta(x)\). Le déplacement \(u_{1}(x,y)\) suivant x dans une section s’écrit :

\[u_{1}=-y\theta(x)=-y\frac{du_{2}}{dx}\]

où \(u_{2}(x)\) est la déflexion de la ligne moyenne. Pour les contraintes, on suppose que \(\sigma_{yy}=0\) (\(\varepsilon_{yy}=-\nu\,\varepsilon_{xx}\)) et les seules contraintes significatives sont \(\sigma_{xx}\) et \(\tau_{xy}\) (avec \(\tau_{xy}\ll\sigma_{xx}\)). on a donc:

\[\sigma_{xx}=E\,\varepsilon_{xx}=E\frac{\partial u_{1}}{\partial x}=-Ey\frac{d\theta}{dx},\,\,\,\,\sigma_{xy}=\frac{E}{2(1+\nu)}\varepsilon_{xy}\]

d’où l’expression du moment fléchissant \(M_{z}\) en fonction de l’inertie \(I\) de la section et du déplacement vertical \(u_{2}\) de la ligne moyenne:

\[M_{z}=E\frac{d\theta}{dx}\int_{S}y^{2}dS=EI\frac{du_{2}^{2}}{dx^{2}}\]

En reportant dans l’équation précédente (2.12), on obtient l’équation d’équilibre moyenne dans la direction \(y\) (comme il n’y a pas de compression, la force axiale est nulle en moyenne dans la section \(\int_{S}\sigma_{xx}ds=0\)):

(2.13)#\[\frac{\partial^{2}}{\partial x^{2}}(EI\frac{\partial u_{2}^{2}}{\partial x^{2}})=p\]

C’est l’équation classique de flexion d’une poutre en statique.

En introduisant l’accélération suivant \(y\), on obtient l’équation de flexion en dynamique qui modélise les vibrations propres d’une poutre en flexion:

(2.14)#\[\rho S\frac{\partial^{2}u_{2}}{\partial t^{2}}=-\frac{\partial^{2}}{\partial x^{2}}(EI\frac{\partial u_{2}^{2}}{\partial x^{2}})\]

2.2.3. Équations de bilan local en mécanique des fluides#

En mécanique des fluides, la variable choisie pour décrire le mouvement est le champ de vitesse \(\overrightarrow{\mathbf{V}}\). L’accélération d’une particule fluide de masse \(dm=\rho dV\) s’écrit alors \(\overrightarrow{\gamma}=\frac{D\overrightarrow{\mathbf{V}}}{Dt}\) (la dérivation \(\frac{D}{Dt}\) s’effectue en suivant le mouvement de la particule). En utilisant une formulation eulérienne, dans un repère fixe lié à l’observateur, cette accélération s’écrit:

\[\begin{split}\overrightarrow{\gamma}=\left(\frac{\partial\overrightarrow{\mathbf{V}}}{\partial t}+\overrightarrow{\mathbf{V}}\otimes\overrightarrow{\mathbf{grad}}\,\overrightarrow{\mathbf{V}}\right)=\left[\begin{array}{c} \frac{\partial v_{1}}{\partial t}+v_{1}\frac{\partial v_{1}}{\partial x}+v_{2}\frac{\partial v_{1}}{\partial y}+v_{3}\frac{\partial v_{1}}{\partial z}\\ \frac{\partial v_{2}}{\partial t}+v_{1}\frac{\partial v_{2}}{\partial x}+v_{2}\frac{\partial v_{2}}{\partial y}+v_{3}\frac{\partial v_{2}}{\partial z}\\ \frac{\partial v_{3}}{\partial t}+v_{1}\frac{\partial v_{3}}{\partial x}+v_{2}\frac{\partial v_{3}}{\partial y}+v_{3}\frac{\partial v_{3}}{\partial z}\end{array}\right]\end{split}\]

L’équilibre d’une particule fluide (figure ci-dessous) résulte de l’équilibre entre l’accélération \(\overrightarrow{\gamma}\), les contraintes \(\overrightarrow{\sigma}\) exercées par l’extérieur (fluide, paroi) et les forces volumiques \(\overrightarrow{f}\):

\[\rho\left[\frac{\partial\overrightarrow{\mathbf{V}}}{\partial t}+\overrightarrow{\mathbf{V}}\otimes\overrightarrow{\mathbf{grad}}\,\overrightarrow{\mathbf{V}}\right]dV=\sum_{\mbox{facettes}}\overrightarrow{\sigma}.\overrightarrow{n}\, dS\,+\overrightarrow{f}\, dV\]
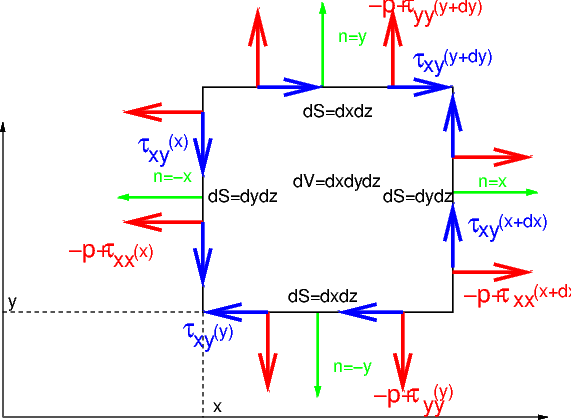
../_images/bilanF1.png

Fig. 2.4 bilan des forces sur une particule fluide#

Pour un fluide le tenseur des contraintes \(\overrightarrow{\sigma}\) est constitué d’une contrainte normale de pression et de contraintes visqueuses \(\overrightarrow{\tau}\), proportionnelles aux gradients du champ de vitesse (fluide Newtonien).

\[\overrightarrow{\sigma}\otimes\overrightarrow{n}=-p\overrightarrow{n}+\mu\left(\overrightarrow{\mathbf{grad}}\,\overrightarrow{\mathbf{V}}+\overrightarrow{\mathbf{grad}}\,^{t}\,\overrightarrow{\mathbf{V}}\right)\otimes\overrightarrow{n}\]

Pour un écoulement bidimensionnel (2D) on obtient les équations d’équilibre suivantes (après passage à la limite):

\[\begin{split}\begin{aligned} \rho\left(\frac{\partial v_{1}}{\partial t}+v_{1}\frac{\partial v_{1}}{\partial x}+v_{2}\frac{\partial v_{1}}{\partial y}\right) & = & -\frac{\partial p}{\partial x}+\frac{\partial}{\partial x}2\mu\left(\frac{\partial v_{1}}{\partial x}\right)+\frac{\partial}{\partial y}\mu\left(\frac{\partial v_{1}}{\partial y}+\frac{\partial v_{2}}{\partial x}\right)+f_{1}\\ \rho\left(\frac{\partial v_{2}}{\partial t}+v_{1}\frac{\partial v_{2}}{\partial x}+v_{2}\frac{\partial v_{2}}{\partial y}\right) & = & -\frac{\partial p}{\partial y}+\frac{\partial}{\partial y}2\mu\left(\frac{\partial v_{2}}{\partial y}\right)+\frac{\partial}{\partial x}\mu\left(\frac{\partial v_{1}}{\partial y}+\frac{\partial v_{2}}{\partial x}\right)+f_{2}\end{aligned}\end{split}\]

Ce sont les équations classiques de Navier-Stokes. A ce système d’équations, il faut ajouter l’équation de conservation de la masse (bilan de masse dans l’élément de volume):

\[\frac{\partial\rho}{\partial t}+div(\rho\overrightarrow{\mathbf{V}})=0\]

et dans le cas général une équation de conservation de l’énergie et une équation d’état. A partir de ces équations de Navier-Stokes on retrouve les approximations classiques:

  1. fluide non visqueux (\(\mu=0\))

    (2.15)#\[\begin{split}\begin{aligned} \frac{\partial\rho}{\partial t}+\frac{\partial\rho v_{1}}{\partial x}+\frac{\partial\rho v_{2}}{\partial y} & = & 0\\ \frac{\partial v_{1}}{\partial t}+v_{1}\frac{\partial v_{1}}{\partial x}+v_{2}\frac{\partial v_{1}}{\partial y} & = & -\frac{1}{\rho}\frac{\partial p}{\partial x} \\ \frac{\partial v_{2}}{\partial t}+v_{1}\frac{\partial v_{2}}{\partial x}+v_{2}\frac{\partial v_{2}}{\partial y} & = & -\frac{1}{\rho}\frac{\partial p}{\partial y} \end{aligned}\end{split}\]

    ce sont les équations d’Euler (avec l’équation de conservation de l’énergie et l’équation d’état)

  2. écoulement non visqueux adiabatique

    dans ce cas l’équation d’énergie et l’équation d’état sont remplacées par l’équation d’adiabaticité \(\frac{p}{\rho^{\gamma}}=cste\), et le système complet d’équation s’écrit:

    (2.16)#\[\begin{split}\begin{aligned} \frac{\partial\rho}{\partial t}+\frac{\partial\rho v_{1}}{\partial x}+\frac{\partial\rho v_{2}}{\partial y} & = & 0\\ \frac{\partial v_{1}}{\partial t}+v_{1}\frac{\partial v_{1}}{\partial x}+v_{2}\frac{\partial v_{1}}{\partial y} & = & -\frac{1}{\rho}\frac{\partial p}{\partial x} \\ \frac{\partial v_{2}}{\partial t}+v_{1}\frac{\partial v_{2}}{\partial x}+v_{2}\frac{\partial v_{2}}{\partial y} & = & -\frac{1}{\rho}\frac{\partial p}{\partial y}\end{aligned}\end{split}\]

    avec \(\frac{dp}{p}=\gamma\frac{d\rho}{\rho}\). Pour un écoulement unidimensionnel, en introduisant la célérité du son \(c^{2}=\gamma\,\frac{p}{\rho}\), on obtient

    (2.17)#\[\begin{split}\begin{aligned} \frac{\partial\rho}{\partial t}+\frac{\partial\rho v_{1}}{\partial x} & = & 0\\ \rho\frac{\partial v_{1}}{\partial t}+\rho v_{1}\frac{\partial v_{1}}{\partial x} & = & -c^{2}\frac{\partial\rho}{\partial x} \end{aligned}\end{split}\]

  3. équations de l’acoustique (en 1D)

    en linéarisant le système d’équation précédant autour d’un état au repos (\(\rho=\rho_{0}\), \(v_{1}=0\)), les fluctuations \(\rho'\) et \(v'_{1}\) vérifient après linéarisation:

    (2.18)#\[\begin{split}\begin{aligned} \frac{\partial\rho'}{\partial t}+\rho_{0}\frac{\partial v'_{1}}{\partial x} & = & 0\\ \rho_{0}\frac{\partial v'_{1}}{\partial t}-c_{0}^{2}\frac{\partial\rho'}{\partial x} & = & 0\end{aligned}\end{split}\]

    qui conduisent, après élimination de \(\rho'\) à l’équation classique des ondes

    (2.19)#\[\frac{\partial^{2}v_{1}}{\partial t^{2}}-c_{0}^{2}\frac{\partial^{2}v'_{1}}{\partial x^{2}}=0\]

  4. fluide incompressible (\(div\,\overrightarrow{\mathbf{V}}=0\))

    si le fluide est incompressible (\(\rho=cste\)), l’équation de conservation de la masse se réduit à une contrainte sur le champ de vitesse: \(div\,\overrightarrow{\mathbf{V}}=0\)

    (2.20)#\[\begin{split}\begin{aligned} \frac{\partial v_{1}}{\partial x}+\frac{\partial v_{2}}{\partial y} & = & 0\\ \frac{\partial v_{1}}{\partial t}+v_{1}\frac{\partial v_{1}}{\partial x}+v_{2}\frac{\partial v_{1}}{\partial y} & = & -\frac{1}{\rho}\frac{\partial p}{\partial x}+\frac{\mu}{\rho}\left(\frac{\partial^{2}v_{1}}{\partial x^{2}}+\frac{\partial^{2}v_{1}}{\partial y^{2}}\right) \\ \frac{\partial v_{2}}{\partial t}+v_{1}\frac{\partial v_{2}}{\partial x}+v_{2}\frac{\partial v_{2}}{\partial y} & = & -\frac{1}{\rho}\frac{\partial p}{\partial y}+\frac{\mu}{\rho}\left(\frac{\partial^{2}v_{2}}{\partial x^{2}}+\frac{\partial^{2}v_{2}}{\partial y^{2}}\right) \end{aligned}\end{split}\]

  5. fluide très visqueux en écoulement stationnaire

    dans ce cas le terme d’accélération est négligeable, et on obtient les équations de Stockes

    (2.21)#\[\begin{split}\begin{aligned} \frac{\partial v_{1}}{\partial x}+\frac{\partial v_{2}}{\partial y} & = & 0\\ -\frac{1}{\rho}\frac{\partial p}{\partial x}+\frac{\mu}{\rho}\left(\frac{\partial^{2}v_{1}}{\partial x^{2}}+\frac{\partial^{2}v_{1}}{\partial y^{2}}\right) & = & 0 \\ -\frac{1}{\rho}\frac{\partial p}{\partial y}+\frac{\mu}{\rho}\left(\frac{\partial^{2}v_{2}}{\partial x^{2}}+\frac{\partial^{2}v_{2}}{\partial y^{2}}\right) & = & 0 \end{aligned}\end{split}\]

  6. fluide parfait incompressible en écoulement potentiel

    les effets de viscosité sont négligés, et l’écoulement est irrotationnel à divergence nulle. Le champ de vitesse \(\overrightarrow{\mathbf{V}}\) découle d’un potentiel \(\Phi\): \(\overrightarrow{\mathbf{V}}=\overrightarrow{grad}\,\Phi\), qui est solution d’une équation de Laplace:

    (2.22)#\[\Delta\Phi=0\]

2.3. Classification des équations#

La résolution numérique des équations d’équilibre précédentes nécessitent des informations supplémentaires (conditions aux limites et/ou initiales). Le choix et le type de ces conditions sont importantes et conditionnent souvent la résolution numérique. De ce point de vue, nous distinguerons 3 grandes classes de problème.

2.3.1. Problèmes elliptiques#

Cette classe de problèmes corresponds à des problèmes stationnaires, qui sont caractéristiques de:

  1. phénomène de diffusion: équations (2.2) et (2.3)

  2. équilibre statique en contraintes: équations (2.8), (2.10) , (2.13)

  3. équilibre de fluide visqueux en écoulement stationnaire: équations (2.21)

  4. équilibre de fluide en écoulement potentiel équations (2.22)

Ces équations sont caractérisées par des dérivées secondes en espace (ou des dérivées quatrièmes) affectées de coefficients de même signe. L’équation type, pour des équations aux dérivées secondes, est l’équation de Laplace:

\[\Delta T=\frac{\partial T^{2}}{\partial x^{2}}+\frac{\partial T^{2}}{\partial y^{2}}=0\]

Pour résoudre cette équation dans un domaine \(\Omega\), il faut se donner une condition aux limites [1] en tous les points de la frontière \(\Gamma=\partial\Omega\) . Cette condition aux limites peut être une:

  1. condition de Dirichlet
    on fixe la valeur de la solution sur une partie \(\Gamma_{0}\) de la frontière: \(T_{\Gamma_{0}}=T_{0}\) (en mécanique des solides on fixe le déplacement, et en mécanique des fluides la vitesse)\

  2. condition de Neuman
    on fixe la valeur de la dérivée normale sur une partie \(\Gamma_{1}\) de la frontière:

    \[\left(\frac{\partial T}{\partial n}\right)_{\Gamma_{1}}=g_{1}\]

    (pour les équations d’équilibres, on fixe les contraintes sur la frontière)

  3. condition mixte (ou Fourier)
    la valeur de la dérivée normale sur une partie \(\Gamma_{2}\) de la frontière est fonction de la solution:

    \[\left(\frac{\partial T}{\partial n}\right)_{\Gamma_{2}}+\alpha T_{\Gamma_{2}}=g_{2}\]

On doit avoir \(\Gamma=\Gamma_{0}\cup\,\Gamma_{1}\cup\,\Gamma_{2}\), et la solution dépend de toutes ces conditions aux limites.

Pour des équations d’ordre 4 (2.13), l’équation type est le bi-laplacien :

\[\Delta^{2}u=\frac{\partial^{4}u}{\partial x^{4}}+\frac{\partial^{4}u}{\partial y^{4}}=0\]

Pour résoudre cette équation dans un domaine \(\Omega\), il faut se donner deux conditions [2] aux limites en chaque point de la frontière \(\Gamma=\partial\Omega\) . Ces 2 conditions peuvent être une combinaison de

  1. conditions de Dirichlet: on impose la valeur de la fonction ou de sa dérivée normale

  2. conditions de Neuman: on impose la valeur de la dérivée seconde ou troisième dans la direction normale.

2.3.2. Problèmes paraboliques#

Cette classe de problèmes corresponds à des problèmes instationnaires, qui sont caractéristiques de:

  1. problème de diffusion instationnaire: équations (2.4), (2.5)

  2. problème de convection-diffusion instationnaire: équations (2.6) , (2.7)

  3. fluide incompressible en écoulement instationnaire: équations (2.20)

Ces équations sont caractérisées par des dérivées secondes en espace et des dérivées premières en temps. L’équation type est l’équation de la chaleur:

\[\frac{\partial T}{\partial t}-\frac{\partial^{2}T}{\partial x^{2}}-\frac{\partial^{2}T}{\partial y^{2}}=0\]

Pour résoudre cette équation dans un domaine \(\Omega\), il faut se donner une condition aux limites en chaque point de la frontière \(\Gamma=\partial\Omega\) (comme pour les problèmes elliptiques) et une condition initiale: la valeur de la solution à \(t=0\).

2.3.3. Problèmes hyperboliques#

Cette classe de problèmes corresponds à des problèmes instationnaires, qui sont caractéristiques de:

  1. phénomènes de propagation
    équations d’Euler en mécanique des fluides (2.15), (2.16),(2.18) et équations de l’acoustique (2.18),(2.19)

  2. phénomènes de vibration
    équations dynamiques en mécanique des solides: (2.9), (2.11) , (2.14)

Ces équations sont caractérisées par des dérivées en temps du même ordre que les dérivées en espace. L’équation type est l’équation des ondes:

\[\frac{\partial^{2}u}{\partial t^{2}}-c^{2}\frac{\partial^{2}u}{\partial x^{2}}=0\]

qui nécessite pour la résoudre 2 conditions initiales: la valeur de la solution et de sa dérivée temporelle à l’instant initial, et des conditions aux limites.

Dans le cas de système hyperbolique (2.16) et (2.17), il faut se donner une condition initiale, mais les conditions aux limites sont plus délicates à formuler et dépendent des ondes caractéristiques qui peuvent se propager dans le milieu.

2.4. Remarques finales#

Tous les problèmes que nous avons passé en revue peuvent être approximés par une méthode d’éléments finis. Cependant l’approximation par éléments finis de certaines équations peut poser des problèmes et nécessiter un traitement spécifique: c’est le cas en mécanique des fluides lorsque les termes de convection deviennent prépondérant. On ne les traitera ici et on renvoie le lecteur à la littérature.

Contenu