4. Eléments finis en 1D

4.1. Une première approche

On veut calculer la température \(T(x)\) dans un barreau de longueur \(L\), de section \(S\) et de conductivité \(k,\) dont l’extrémité gauche est isotherme (i.e \(T(0)=T_{e}\)), et l’extrémité droite reçoit un flux de chaleur \(\Phi_{e}\). En plus de la conduction dans le solide (le flux de chaleur par conduction dans une section s’écrit \(\Phi_{1}=-kS\frac{dT}{dx}\), le barreau échange de la chaleur par convection avec l’air ambiant à la température \(T_{a}\) sur toute sa longueur. En notant \(h\) le coefficient d’échange par convection par unité de surface, le flux de chaleur par convection s’écrit pour un élément de longueur \(dx\) : \(\Phi_{2}=h\,dx\,p\,(T-T_{a})\) (où \(p\) est le périmètre de la section du barreau)).

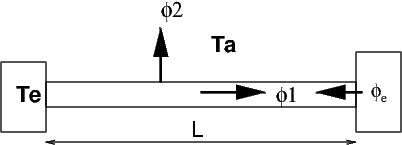
Fig. 4.1 Température dans un barreau

En notant \(K=kS\), et \(\alpha=h\,p\), l’équation d’équilibre s’écrit: trouver \(T(x)\) solution du système (4.1)

(4.1)\[\begin{split}\left\{ \begin{array}{c} -\frac{d}{dx}(K\frac{dT}{dx})+\alpha T=\alpha T_{a}\\ T(0)=T_{e},\,-K\frac{dT}{dx}(L)=\Phi_{e} \end{array}\right.\end{split}\]

4.1.1. Formulation faible

La formulation faible de ce problème s’obtiens en multipliant l’équation par une fonction test \(v(x)\), et en intégrant sur le domaine d’étude. Il vient:

\[\int_{0}^{L}(-\frac{d}{dx}(K\frac{dT}{dx})\,v(x)\,dx+\int_{0}^{L}\alpha T(x)\,v(x)\,dx=\int_{0}^{L}\alpha T_{a}v(x)\,dx\]

Pour tenir compte des conditions aux limites et symétriser le problème, on effectue une intégration par partie sur les termes de plus haut degré:

\[\int_{0}^{L}K\frac{dT}{dx}\,\frac{dv}{dx}\,dx-[K\frac{dT}{dx}v(x)]_{0}^{L}+\int_{0}^{L}\alpha T(x)\,v(x)\,dx=\int_{0}^{L}\alpha T_{a}v(x)\,dx\]

Si le problème est bien posé, le terme de bord \([K\frac{dT}{dx}v(x)]_{0}^{L}\) doit pouvoir se calculer en fonction des conditions aux limites. Pour cela on interprète la fonction test \(v(x)\) comme une variation \(\delta T(x)\) de la solution \(T(x)\). Si on fixe la valeur de la solution en un point (condition de Dirichlet), sa variation est nulle et la fonction test \(v(x)\) doit s’annuler en ce point. Pour notre problème, on doit donc imposer à \(v(x)\) de s’annuller en \(x=0\) puisque la valeur de \(T(x)\) est fixé en ce point. Par contre en \(x=L\), on impose aucune contrainte sur \(v(x)\) et on utilise la condition de flux pour calculer le terme de bord. C’est une condition au limite de Neuman. Avec ces conditions, le terme de bord se réduit à \(\Phi_{e}*v(L)\), et la formulation faible s’écrit:

(4.2)\[\begin{split}\left\{ \begin{array}{l} \mbox{Trouvez }T(x)\,\mbox{ avec }T(0)=T_{e}\mbox{ t.q.}\\ \int_{0}^{L}K\frac{dT}{dx}\,\frac{dv}{dx}\,dx+\int_{0}^{L}\alpha T(x)\,v(x)\,dx=\int_{0}^{L}\alpha T_{a}v(x)\,dx-\Phi_{e}v(L)\\ \mbox{pour toute fonction test }v(x)\mbox{ vérifiant }v(0)=0 \end{array}\right.\end{split}\]

On remarque que dans cette formulation, seule la condition au limite en \(x=0\) est imposé de façon explicite. On parle alors de condition forte. La condition en \(x=L\) n’est pas imposée explicitement, mais est prise en compte dans la formulation intégrale. C’est une condition faible.

Exercice: Montrer que la formulation faible (4.2) est équivalente au problème de minimisation (4.3)

(4.3)\[\begin{split}\left\{ \begin{array}{l} \mbox{Trouvez }T(x)\,\mbox{ avec }T(0)=T_{e}\mbox{ t.q.}\\ J(T)=\frac{1}{2}\int_{0}^{L}K(\frac{dT}{dx})^{2}\,dx+\frac{1}{2}\int_{0}^{L}\alpha T(x)^{2}\,dx-\int_{0}^{L}\alpha T_{a}T(x)\,dx+\Phi_{e}T(L)\\ \mbox{soit minimum i.e. }J(T)\le J(V)\mbox{ pour toute fonction }V(x)\mbox{ vérifiant }V(0)=T_{e} \end{array}\right.\end{split}\]

4.1.2. Interpolation par éléments finis

Pour résoudre le problème (4.2) (dont il n’existe en général pas de solution analytique), on recherche une solution numérique approchée \(T^{h}(x)\). En éléments finis, cette solution approchée est construite à partir de 2 données:

1. un maillage \(\mathcal{M}^{h}\)du domaine de calcul \(\mathcal{D}\),

2. un choix d’interpolation \(\mathcal{P}^{k}\) sur ce maillage.

Pour notre domaine de calcul unidimensionnel \(\mathcal{D}=[0,L]\), le maillage correspond à un découpage de \(\mathcal{D}\) en N segments:

\[\mathcal{D}=\bigcup_{i=1}^{N}[x_{i-1},x_{i}]\]

Sur chaque segment, on choisit une interpolation de type polynomial. Le type de l’interpolation dépend du problème à traiter. Pour notre problème elle doit en particulier respecter les contraintes suivantes:

1. les intégrales dans la formulation faible (4.2) ou variationnelle (4.3) doivent pouvoir être calculer,

2. la solution approchée est globalement continue.

4.1.2.1. construction de l’interpolation

La première condition impose que sur chaque élément le polynôme d’interpolation \(p(x)\) soit au moins de degré 1 pour pouvoir calculer les dérivées premières de la solution qui interviennent dans la formulation faible (4.2) . Sur chaque élément \([x_{i-1},x_{i}]\), la solution approchée est donc un polynôme de degré \(k\ge1\). Pour déterminer ce polynôme, il faut choisir \(k+1\) points d’interpolation \(\{P_{j}\}_{j=0,k}\), et calculer les valeurs de la solution en ces points \(\{Y_{j}\}_{j=0,k}\) (les \(k+1\) relations \(Y_{j}=p(X_{j})\) permettent alors la détermination unique des coefficients du polynôme d’interpolation):

\[p(x)=\sum_{j=1}^{k}a_{j}x^{j}\,\mbox{ avec }\,p(X_{j})=Y_{j}\,(j=0,k)\]

La seconde condition impose la continuité de l’interpolation aux points de maillage. Pour assurer cette propriété, on choisit comme points d’interpolation les 2 extrémités du segment, et éventuellement \(k-1\) autres points équi-répartits sur l’intervalle. Pour un polynôme d’ordre 1 sur \([x_{i-1},x_{i}]\) (éléments finis \(\mathcal{P}^{1}\)), on utilise 2 points d’interpolation: les 2 extrémités du segment \(\{P_{0}=x_{i-1},\,P_{1}=x_{i}\}\). Pour un polynôme d’ordre 2 (éléments finis \(\mathcal{P}^{2}\)), on utilise 3 points d’interpolation: les 2 extrémités du segment, et un point intermédiaire que l’on choisit naturellement au milieu du segment \(\{P_{0}=x_{i-1},\,P_{1}=\frac{x_{i-1}+x_{i}}{2},\,P_{2}=x_{i}\}\).

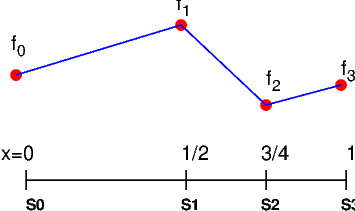
Fig. 4.2 Maillage et interpolation \(P^{1}\)

Considérons par exemple le maillage du domaine \(\mathcal{D}=[0,1]\) (figure ci-dessus) suivant:

\[\mathcal{M}^{h}=[0,\frac{1}{2}]\bigcup[\frac{1}{2},\frac{3}{4}]\bigcup[\frac{3}{4},1]\]

L’interpolation \(u^{h}(x)\) par éléments finis \(\mathcal{P}^{1}\) de la fonction \(f(x)\) s’écrit:

(4.4)\[\begin{split}u^{h}(x)=\left\{ \begin{array}{l} 2(f_{1}-f_{0})x+f_{0}\,\mbox{ si }\,x\le\frac{1}{2}\\ 4(f_{2}-f1)x-2f_{2}+3f_{1}\,\mbox{ si }\,\frac{1}{2}\le x\le\frac{3}{4}\\ (4f_{3}-4f_{2})x-3f_{3}+4f_{2}\,\mbox{ si }\,\frac{3}{4}\le x\le1 \end{array}\right.\end{split}\]

où \(\{f_{0},f_{1},f_{2},f_{3}\}\) sont les valeurs nodales de \(f\) aux points de maillage \(\{0,\frac{1}{2},\frac{3}{4}1\}\). C’est une fonction linéaire par morceau et continue sur l’intervalle d’étude \(\mathcal{D}\). Sa dérivée \(\frac{du^{h}}{dx}\)s’écrit:

\[\begin{split}\frac{du^{h}}{dx}(x)=\left\{ \begin{array}{l} 2(f_{1}-f_{0})\,\mbox{ si }\,x<\frac{1}{2}\\ 4(f_{2}-f1)x\,\mbox{ si }\,\frac{1}{2}<x<\frac{3}{4}\\ (4f_{3}-4f_{2})x\,\mbox{ si }\,\frac{3}{4}<x<1 \end{array}\right.\end{split}\]

C’est une fonction constante par morceau et discontinue aux points de maillage.

Exercice: calculer pour ce même maillage l’interpolation par éléments finis \(\mathcal{P}^{2}\)

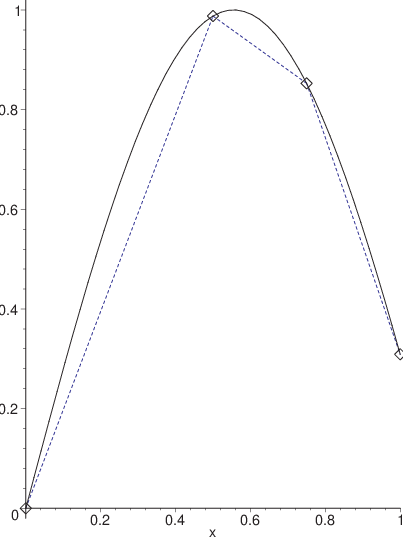
Fig. 4.3 Interpolation éléments finis d’une fonction sur un maillage de 3 segments \(\diamondsuit\) avec des polynômes \(P_{1}\) \((...)\) et \(P_{2}\) \((--)\)

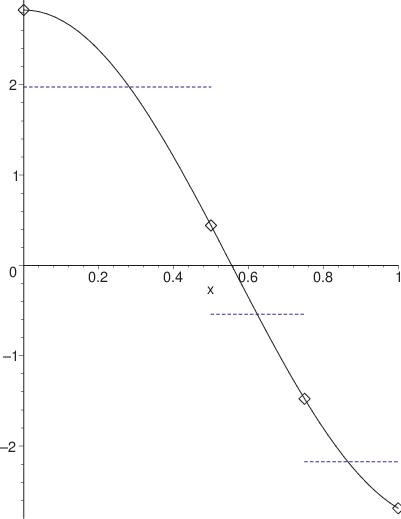
Fig. 4.4 Interpolation éléments finis de sa dérivée sur un maillage de 3 segments \(\diamondsuit\) avec des polynômes \(P_{1}\) \((...)\) et \(P_{2}\) \((--)\)

Sur la figure Fig. 4.3, on a tracé l’interpolation par éléments finis de la fonction \(f(x)=\sin(0.8\pi x)\) et sur la figure Fig. 4.4 de sa dérivée sur ce maillage de 3 segments en utilisant des polynômes de degré 1 et 2. On constate que l’approximation \(\mathcal{P}^{2}\) est évidemment plus précise que l’approximation \(\mathcal{P}^{1}\), et que ces deux approximations ont une dérivée qui est discontinue aux points de maillage.

4.1.2.2. erreur d’interpolation

On rappelle que l’erreur entre une fonction \(f(x)\) et son polynôme d’interpolation \(p(x)\) de degré k s’écrit:

\[f(x)-p(x)=\frac{\prod_{j=0}^{k}(x-P_{j})}{(k+1)!}f^{(k+1)}(\chi)\]

où les \(\{P_{j}\}_{j=0,k}\) sont les points d’interpolation. Pour une approximation linéaire sur un segment \([x_{i-1},x_{i}]\), l’erreur d’interpolation s’écrit

\[f(x)-p(x)=\frac{(x-x_{j})(x-x_{j-1})}{2}\frac{d^{2}f}{dx^{2}}(\chi)\]

On vérifie que l’erreur s’annule aux points d’interpolation et est proportionnelle à la dérivée seconde de \(f(x).\)

A partir de cette relation locale, on peut déduire par calcul directe les majorations d’erreurs suivantes pour la norme du maximum et la norme moyenne de l’erreur sur l’intervalle \([x_{j-1},x_{j}]\) de longueur \(h=x_{j}-x_{j-1}\).

\[\begin{split}\begin{aligned} \max_{x\in[x_{j-1},x_{j}]}(|f(x)-p(x)|) & \le & \frac{h^{2}}{8}\max_{[x_{j-1},x_{j}]}(|\frac{d^{2}f}{dx^{2}}(\chi)|)\\ \sqrt{\int_{x_{j-1}}^{x_{j}}(f(x)-p(x))^{2}dx} & \le & \frac{h^{2}}{8}\sqrt{\int_{x_{j-1}}^{x_{j}}(\frac{d^{2}f}{dx^{2}}(\chi))^{2}dx}\end{aligned}\end{split}\]

On vérifie que l’erreur moyenne d’approximation par éléments finis \(\mathcal{P}^{1}\) est en \(\theta(h^{2})\), i.e. est proportionnelle au carré de la longueur des éléments.

\[\left\Vert f(x)-p(x)\right\Vert \leq Ch^{2}\]

Exercice: montrez que l’erreur avec des éléments finis \(\mathcal{P}^{2}\) est en \(\theta(h^{3})\)

4.1.3. Approximation par éléments finis

L’approximation par éléments finis est définie de façon locale sur chaque élément (4.4) . De façon à pouvoir la manipuler plus facilement, on va l’exprimer de façon globale.

L’approximation par éléments finis \(u^h(x)\) est définie par sa valeur aux \(N_n\) points nodaux \({u_i}_{i=0,N_n-1}\) et peut s’écrire de façon générique

\[ u_h(x) = \sum_{i=0}^{N_n-1} u_i \phi_i(x) \]

dans cette expression \(u_i\) représente la valeur nodale au noeud \(i\) et \(\phi_i(x)\) la fonction de base associée au noeud \(i\), qui dépend du type d’interpolation utilisée. On utilise ici une numérotation à partir de 0.

Pour déterminer les fonctions de base \(\phi_i(x)\), on va tout d’abord déterminer une expression générique de l’approximation sur un élément \([x_{j-1},x_{j}]\).

4.1.3.1. fonctions de forme

Pour ce faire on introduit une transformation géométrique qui permet de passer d’un élément quelconque \([x_{j-1},x_{j}]\) à un élément de référence \([0,1]\), sur lequel on va définir l’approximation de manière générique. Cette transformation affine \(\mathcal{F}^{j}\) s’écrit:

(4.5)\[\begin{split}\mathcal{F}^{j}\,\left\{ \begin{array}{c} [x_{j-1},x_{j}]\Longrightarrow[0,1]\\ x\longrightarrow\chi=\frac{x-x_{j-1}}{x_{j}-x_{j-1}} \end{array}\right.\end{split}\]

qui correspond au changement de variable: \(x \rightarrow \chi\)

\[ \chi=\frac{x-x_{j-1}}{x_{j}-x_{j-1}} \]

Sur cet élément de référence, on choisit \(p+1\) points d’interpolation régulièrement espacés \(\{\chi_{j}=\frac{j}{k}\}_{j=0,k}\),. Un polynôme \(P(\chi)\) de degré \(p\) s’écrit alors sous la forme générique de Lagrange:

\[P(\chi)=\sum_{j=0}^{p}P(\frac{j}{p})L_{j}(\chi)\,\mbox{ avec }\,L_{j}(\chi)=\frac{\prod_{i\ne j}^{i=0,p}(\chi-\frac{i}{p})}{\prod_{i\ne j}^{i=0,p}(\frac{j}{p}-\frac{i}{p})}\]

Le polynôme \(P(\chi)\) est donc une combinaison linéaire des \(p+1\) polynômes de Lagrange \(L_{j}(\chi)\) . Les coefficients de cette combinaison linéaire sont les valeurs du polynôme aux points d’interpolation \(P(\frac{j}{p})\). Le polynôme de Lagrange \(L_{j}(\chi)\) est le polynôme de degré \(k\) associé au noeud \(\chi_{j}\) qui vaut 1 au point d’interpolation \(\chi_{j}=\frac{j}{p}\), et 0 aux \(p\) autres points d’interpolation \(\{\chi_{i}=\frac{i}{p}\}_{i=0,p}^{i\ne j}\). Ces polynômes de Lagrange définissent les \(p+1\) « fonctions de forme » \({N_i(\chi)}_{i=1,p+1}\) de l’approximation \(\mathcal{P}^{p}\).

Pour un élément \(\mathcal{P}^{1}\), on a 2 points d’interpolation et donc 2 fonctions de forme:

(4.6)\[N_1(\chi)=\chi\,\mbox{ et }\,N_2(\chi)=1-\chi\]

et tout polynôme de degré 1 s’écrit sur l’intervalle de référence:

\[P(\chi)=P(0)\,N_{1}(\chi)+P(1)\,N_{2}(\chi)\]

Exercice: déterminer les 3 fonctions de formes \(N_1,N_2,N_3\) pour un élément \(\mathcal{P}^{2}\)

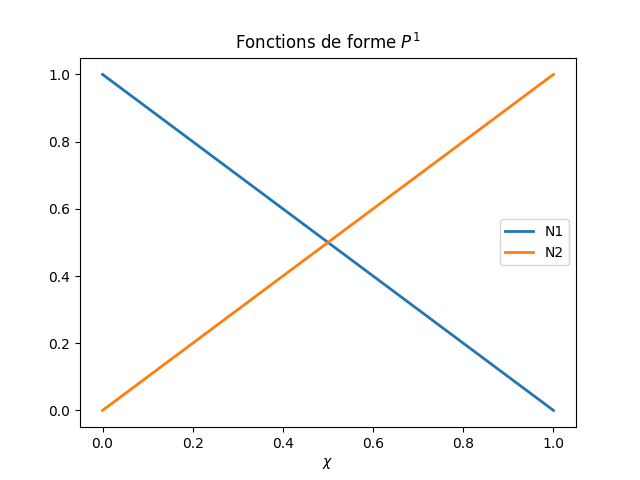
Fig. 4.5 fonctions de forme \(\mathcal{P}^{1}\)

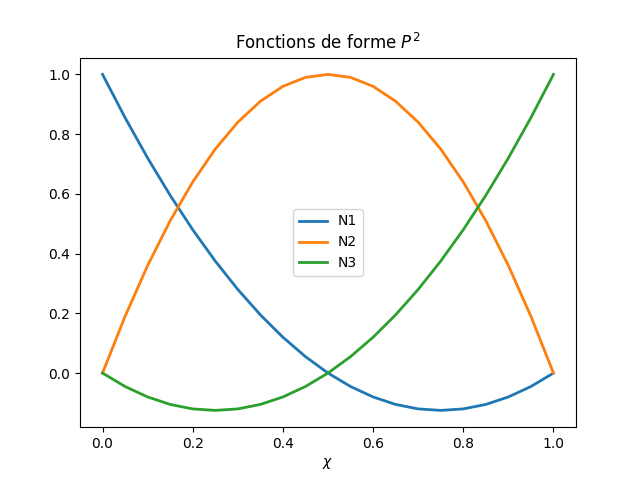
Fig. 4.6 fonctions de forme \(\mathcal{P}^{2}\) Température dans un barreau

En utilisant le changement de variable \(\chi=\mathcal{F}^{j}(x)\) (4.5), un polynôme de degré 1 sur un élément \(j\): \([x_{j-1},x_{j}]\) s’écrit:

\[P(x)=P(x_{j-1})\,N_{1}(\mathcal{F}^{j}(x))+P(x_{j})\,N_{2}(\mathcal{F}^{j}(x))\]

Attention: lorsque l’on calcule la dérivée de l’approximation élément finis, la dérivée dans l’élément \([x_{j-1},x_{j}]\) n’est pas égale à la dérivée dans l’élément de référence. Il faut tenir compte du changement de variable:

\[\frac{dP}{dx}(x)=\frac{dP}{d\chi}(\chi)\frac{d\chi}{dx}\,\mbox{ avec }\,\frac{d\chi}{dx}=\frac{1}{h_{j}}\,\mbox{ et }\,h_{j}=x_{j}-x_{j-1}\]

Pour un polynôme de degré 1, on obtient:

\[\begin{split}\begin{aligned} \frac{dP}{dx}(x) & = & p(x_{j-1})\frac{dN_{1}}{d\chi}\frac{1}{h_{j}}+p(x_{j})\frac{dN_{2}}{d\chi}\frac{1}{h_{j}}\\ & = & \frac{1}{h_{j}}(P(x_{j})-P(x_{j-1}))\end{aligned}\end{split}\]

Exercice: calculer la dérivée d’une approximation élément finis \(\mathcal{P}^{2}\)

4.1.3.2. fonctions de base

Avec ces nouvelles notations, l’approximation élément finis \(u^{h}\) dans l’équation (4.4) s’écrit

\[\begin{split}u^{h}(x)=\left\{ \begin{array}{l} f_{0}N_{1}(2x)+f_{1}N_{2}(2x)\,\mbox{ si }\,x\le\frac{1}{2}\\ f_{1}N_{1}(4x-2)+f_{2}N_{2}(4x-2)\,\mbox{ si }\,\frac{1}{2}\le x\le\frac{3}{4}\\ f_{2}N_{1}(4x-3)+f_{3}N_{2}(4x-3)\,\mbox{ si }\,\frac{3}{4}\le x\le1 \end{array}\right.\end{split}\]

on constate que \(u^{h}\) est une fonction linéaire des 4 valeurs nodales \(\{f_{0},f_{1},f_{2},f_{3}\}\). On peut donc écrire \(u^{h}(x)\) comme une combinaison linéaire de ces valeurs:

\[u^{h}(x)=f_{0}\phi_{0}(x)+f_{1}\phi_{1}(x)+f_{2}\phi_{2}(x)+f_{3}\phi_{3}(x)\]

où les fonctions \(\{\phi_{0},\phi_{1},\phi_{2},\phi_{3}\}\) sont définies par

(4.7)\[\begin{split}\begin{aligned} \phi_{0}(x)=N_{1}(2x)\,\mbox{ si }\,x\le\frac{1}{2}\;\mbox{ , }& \phi_{0}(x)=0\,\mbox{ sinon} \\ \phi_{1}(x)=N_{2}(2x)\,\mbox{ si }\,x\le\frac{1}{2}\; \mbox{ , }& \phi_{1}(x)=N_{1}(4x-2)\,\mbox{ si }\frac{1}{2}\le x\le\frac{3}{4} \mbox{ , }& \phi_{1}(x)=0\,\mbox{ sinon} \\ \phi_{2}(x)=N_{2}(4x-2)\,\mbox{ si }\frac{1}{2}\le x\le\frac{3}{4}\; \mbox{ , }& \phi_{2}(x)=N_{1}(4x-3)\,\mbox{ si }\frac{3}{2}\le x\le1 \mbox{ , }& \phi_{2}(x)=0\,\mbox{ sinon}\\ \phi_{3}(x)=N_{2}(4x-3)\,\mbox{ si }\frac{3}{2}\le x\le 1\; \mbox{ , }& \phi_{3}(x)=0\,\mbox{ sinon}\end{aligned}\end{split}\]

Ces fonctions sont appelées fonctions de base de l’approximation éléments finis. Elles sont tracées sur la figure ci-dessous ainsi que les fonctions de base \(P^{2}\).

Exercice: pour ce même maillage, déterminer les fonctions de base \(\mathcal{P}^{2}\)

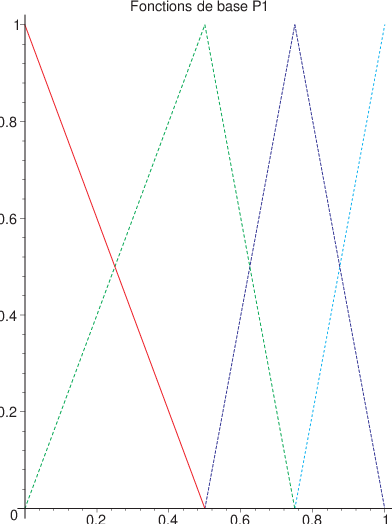
Fig. 4.7 fonctions de base pour une approximation \(\mathcal{P}^{1}\)

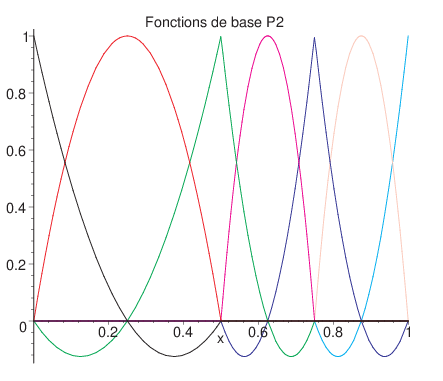
Fig. 4.8 fonctions de base pour une approximation \(\mathcal{P}^{2}\)

De façon générale, l’approximation par éléments finis \(u^{h}\) peut s’écrire sous la forme:

\[u^{h}(x)=\sum_{i=0}^{N_{n}-1}u^{h}(P_{i})\,\phi_{i}(x)\]

où \(N_{n}\) est le nombre total de points nodaux \(\{P_{i}\}\), et \(\phi_{i}(x)\) les fonctions de base associées. Pour un maillage de \(N_{e}\) éléments \(\mathcal{P}^{1}\), le nombre de points nodaux est égale à \(N_{n}=N_{e}+1.\) Ces fonctions de base vérifient la propriété importante suivante: la fonction de base \(\phi_{i}\) vaut 1 au noeud \(P_{i}\) et 0 sur tout les autres noeuds \(\{P_{j}\}_{j\ne i}\)

\[\phi_{i}(P_{j})=\delta_{ij}\,\,\forall i,j=1,N_{n}\]

Exercice: montrez que pour des éléments \(\mathcal{P}^{k}\), le nombre de points nodaux est \(N_{n}=k.N_{e}+1\)

4.1.4. Formulation faible discrète

On cherche une approximation par éléments finis de la solution du problème (4.2). Pour cela on choisit le maillage suivant du domaine de calcul \([0,L]:\)

\[\mathcal{M}^{h}=[0,\frac{L}{2}]\bigcup[\frac{L}{2},\frac{3L}{4}]\bigcup[\frac{3L}{4},L]\]

On choisit ensuite sur ce maillage une approximation par élément finis \(\mathcal{P}^{1}\) de la solution approchée \(T^{h}\). Le nombre de points nodaux est donc égale à \(Nn=4\), et \(T^{h}\) s’écrit:

\[T^{h}(x)=T(0)\,\phi_{0}(x)+T(\frac{L}{2})\,\phi_{1}(x)+T(\frac{3L}{4})\,\phi_{2}(x)+T(L)\,\phi_{3}(x)\]

On notera \(\{T_{i}^ {}\}_{i=0,3}\) les valeurs nodales \(\{T(0),T(\frac{L}{2}),T(\frac{3L}{4}),T(1)\}\), ce qui permet d’écrire \(T^{h}\) sous la forme:

\[T^{h}(x)=\sum_{i=0}^{3}T_{i}\,\phi_{i}(x)\]

La solution du problème (4.2) doit vérifier les conditions aux limites fortes (Dirichlet), i.e.:

\[T^{h}(x=0)=T_{e}\]

La valeur nodale \(T_{0}^ {}=T(0)\) est donc fixée, et \(T^{h}\) s’écrit:

(4.8)\[T^{h}(x)=T_{e}\phi_{0}(x)+\sum_{i=1}^{3}T_{i}\,\phi_{i}(x)\]

Le problème discrétisé possède donc 3 degrés de liberté (ou inconnues): les 3 valeurs nodales \(\{T_{i}\}_{i=1,3}\). De façon générale après application des \(Nc\) conditions aux limites fortes, la solution élément finis possède \(N=N_{n}-N_{c}\) degré de liberté. Pour un maillage de \(N_{e}\) éléments \(\mathcal{P}^{1}\), on a \(N=N_{e}+1-N_{c}\).

En remplaçant la solution exacte par la solution approchée (4.8) dans l’équation (4.2), il vient la formulation faible discrète:

(4.9)\[\begin{split}\begin{aligned} \int_{0}^{L}K\left(T_{e}\frac{d\phi_{0}}{dx}+\sum_{j=1}^{3}T_{j}\frac{d\phi_{j}}{dx}\right)\frac{dv^{h}}{dx}\,dx+\int_{0}^{L}\alpha\left(T_{e}\phi_{0}+\sum_{j=1}^{3}T_{j}\phi_{j}\right)v^{h}\,dx\\ =\int_{0}^{L}\alpha T_{a}v^{h}\,dx-\Phi_{e}v^{h}(L)\end{aligned}\end{split}\]

Ayant la forme (4.8) de la solution approchée \(T^{h}=T^{h}(T_{1},T_{2},T_{3})\), on peut en déduire les fonctions tests \(v^{h}(x)\) associées, puisque ce sont des variations \(\delta T^{h}\) de \(T^{h}\) qui s’écrivent:

(4.10)\[v^{h}(x)=\delta T^{h}=\sum_{i=1}^{3}\delta T_{i}\,\phi_{i}(x)\]

On vérifie que ces fonctions tests s’annulent en \(x=0\) (condition de Dirichlet). Ces fonctions tests sont des combinaisons linéaires des 3 fonctions de base \(\{\phi_{i}(x)\}_{i=1,3}\) associées aux 3 degrés de liberté \(\{T_{i}\}_{i=1,3}\) de la solution approchée.

En choisissant comme fonctions tests \(v^{h}\) dans (4.9), respectivement les 3 fonctions de base \(\{\phi_{i}(x)\}_{i=1,3}\), on obtiens les 3 équations qui vont permettre de calculer les 3 inconnues \(\{T_{i}\}_{i=1,3}\):

\[\begin{split}\begin{aligned} \int_{0}^{L}K(T_{e}\frac{d\phi_{0}}{dx}+\sum_{j=1}^{3}T_{j}\frac{d\phi_{j}}{dx})\frac{d\phi_{1}}{dx}dx+\int_{0}^{L}\alpha(T_{e}\phi_{0}+\sum_{j=1}^{3}T_{j}\phi_{j})\phi_{1}dx\\ =\int_{0}^{L}\alpha T_{a}\phi_{1}dx-\Phi_{e}\phi_{1}(L)\\ \int_{0}^{L}K(T_{e}\frac{d\phi_{0}}{dx}+\sum_{j=1}^{3}T_{j}\frac{d\phi_{j}}{dx})\frac{d\phi_{2}}{dx}dx+\int_{0}^{L}\alpha(T_{e}\phi_{0}+\sum_{j=1}^{3}T_{j}\phi_{j})\phi_{2}dx\\ =\int_{0}^{L}\alpha T_{a}\phi_{2}dx-\Phi_{e}\phi_{2}(L)\\ \int_{0}^{L}K(T_{e}\frac{d\phi_{0}}{dx}+\sum_{j=1}^{3}T_{j}\frac{d\phi_{j}}{dx})\frac{d\phi_{3}}{dx}dx+\int_{0}^{L}\alpha(T_{e}\phi_{0}+\sum_{j=1}^{3}T_{j}\phi_{j})\phi_{3}dx\\ =\int_{0}^{L}\alpha T_{a}\phi_{3}dx-\Phi_{e}\phi_{3}(L)\end{aligned}\end{split}\]

C’est un système linéaire de 3 équations à 3 inconnues, qui s’écrit après regroupement des termes sous la forme matricielle: \({\bf A.X=B}\), où la matrice \({\bf A,}\) le second membre \({\bf B}\) et le vecteur inconnu \({\bf X}\) sont donnés par:

\[\begin{split}\mathbf{A}=\left[\begin{array}{ccc} \int_{0}^{L}(K\frac{d\phi_{1}}{dx}\frac{d\phi_{1}}{dx}+\alpha \phi_{1}\phi_{1})dx & \int_{0}^{L}(K\frac{d\phi_{2}}{dx}\frac{d\phi_{1}}{dx}+\alpha \phi_{2}\phi_{1})dx & \int_{0}^{L}K(\frac{d\phi_{3}}{dx}\frac{d\phi_{1}}{dx}+\alpha \phi_{3}\phi_{1})dx\\ \int_{0}^{L}(K\frac{d\phi_{1}}{dx}\frac{d\phi_{2}}{dx}+\alpha \phi_{1}\phi_{2})dx & \int_{0}^{L}(K\frac{d\phi_{2}}{dx}\frac{d\phi_{2}}{dx}+\alpha \phi_{2}\phi_{2})dx & \int_{0}^{L}K(\frac{d\phi_{3}}{dx}\frac{d\phi_{2}}{dx}+\alpha \phi_{3}\phi_{2})dx\\ \int_{0}^{L}(K\frac{d\phi_{1}}{dx}\frac{d\phi_{3}}{dx}+\alpha \phi_{1}\phi_{3})dx & \int_{0}^{L}(K\frac{d\phi_{2}}{dx}\frac{d\phi_{3}}{dx}+\alpha \phi_{2}\phi_{3})dx & \int_{0}^{L}K(\frac{d\phi_{3}}{dx}\frac{d\phi_{3}}{dx}+\alpha \phi_{3}\phi_{3})dx \end{array}\right]\end{split}\]

\[\begin{split}\mathbf{X}=\left[\begin{array}{c} T_{1}\\ T_{2}\\ T_{3} \end{array}\right]\label{rel7}\end{split}\]

\[\begin{split}\mathbf{B}=\left[\begin{array}{c} \int_{0}^{L}\alpha T_{a}\phi_{1}dx-\Phi_{e}\phi_{1}(L)-T_{e}\int_{0}^{L}(K\frac{d\phi_{0}}{dx}\frac{d\phi_{1}}{dx}+\alpha \phi_{0}\phi_{1})dx\\ \int_{0}^{L}\alpha T_{a}\phi_{2}dx-\Phi_{e}\phi_{2}(L)-T_{e}\int_{0}^{L}(K\frac{d\phi_{0}}{dx}\frac{d\phi_{2}}{dx}+\alpha \phi_{0}\phi_{2})dx\\ \int_{0}^{L}\alpha T_{a}\phi_{3}dx-\Phi_{e}\phi_{3}(L)-T_{e}\int_{0}^{L}(K\frac{d\phi_{0}}{dx}\frac{d\phi_{3}}{dx}+\alpha \phi_{0}\phi_{3})dx \end{array}\right]\end{split}\]

soit sous forme générique:

(4.11)\[\begin{split}\begin{aligned} \mathbf{A}_{ij}=\int_{0}^{L}K\frac{d\phi_{j}}{dx}\frac{d\phi_{i}}{dx}dx+\int_{0}^{L}\alpha \phi_{j}\phi_{i}\,dx\mbox{\, et\, }\nonumber \\ \mathbf{B}_{i}=\int_{0}^{L}\alpha T_{a}\phi_{i}dx-\Phi_{e}\phi_{i}(L)-T_{e}\int_{0}^{L}(K\frac{d\phi_{0}}{dx}\frac{d\phi_{i}}{dx}+\alpha \phi_{0}\phi_{i})dx \end{aligned}\end{split}\]

On remarque que la matrice \(\mathbf{A}\) est symétrique puisque la formulation faible est elle même symétrique en \(T\) et \(v\).

La solution de la formulation faible discrète (4.9) s’obtient donc par résolution d’un système linéaire. Il nous reste à calculer la matrice \(\mathbf{A}\) et le second membre \(\mathbf{B}\) , dont les coefficients sont des intégrales des fonctions de base. Connaissant l’expression de ces fonctions de base (4.7), un calcul directe des intégrales permettrait d’obtenir la matrice \(\mathbf{A}\) et le vecteur \(\mathbf{B}\). Cette approche n’est possible que pour un petit nombre de degré de liberté, et on préfère utiliser une approche systématique pour le calcul de \(\mathbf{A}\) et \(\mathbf{B}\) , qui s’appelle l’assemblage.

4.1.5. Assemblage

Pour le calcul des intégrales, nous allons tout d’abord donner quelques propriétés des fonctions de base:

1. une fonction de base \(\phi_{i}(x)\) est non nulle uniquement sur les éléments du maillage auxquels appartient le noeud \(P_{i}\) , c’est à dire sur une toute petite partie du maillage. On dit que \(\phi_{i}(x)\) a un support compact. Pour une fonction de base \(\phi_{i}(x)\) de type \(\mathcal{P}^{1}\), ce support est le segment \([x_{i-1},x_{i+1}]\).

2. en conséquence, le produit \(\phi_{i}(x)\,\phi_{j}(x)\) de 2 fonctions de bases est en générale toujours nulle, sauf si l’intersection des supports est non vide (ce qui est rare car les supports sont petits). Dans ce dernier cas le produit est non nulle uniquement sur l’intersection des 2 supports. Pour les fonctions de base \(\mathcal{P}^{1}\), on vérifie que:

   \[\phi_{i}(x)\,\phi_{j}(x)=0\,\mbox{ sauf si }\,j=i-1,\,i,\,i+1\]

4.1.5.1. assemblage de la matrice

D’après la relation (4.9), la calcul de \({\bf {A}_{ij}}\) fait intervenir 2 types d’intégrale. On décompose alors \({\bf A}\) en 2 matrices:

\[\mathbf{A}=\mathbf{K}+\mathbf{M}\,\mbox{ avec }\,\mathbf{K}_{ij}=\int_{0}^{L}K\frac{d\phi_{j}}{dx}\frac{d\phi_{i}}{dx}dx,\,\mathbf{M}_{ij}=\int_{0}^{L}\alpha \phi_{j}\phi_{i}\,dx\]

la matrice \({\bf K}\) est appelée matrice de rigidité et \({\bf M}\) matrice de masse.

Pour calculer ces intégrales on décompose l’intégrale sur le domaine \([0,L]\) en somme d’intégrales élémentaires sur chaque élément \([x_{l-1},x_{l}]\).

\[\mathbf{K}_{ij}=\sum_{l=1}^{Ne}\int_{x_{l-1}}^{x_{l}}K\frac{d\phi_{j}}{dx}\frac{d\phi_{i}}{dx}dx\,\mbox{ et }\mathbf{M}_{ij}=\sum_{l=1}^{Ne}\int_{x_{l-1}}^{x_{l}}\alpha \phi_{j}\phi_{i}\,dx\]

On est donc ramené à un calcul d’intégrales élémentaires sur chaque élément. En utilisant les propriétés des fonctions de base, chaque intégrale élémentaire est non nulle sur un élément \([x_{l-1},x_{l}]\) si et seulement si les noeuds \(P_{i}\) et \(P_{j}\) appartiennent tous les deux à cet élément. Pour des éléments \(\mathcal{P}^{1}\), on a 4 cas possibles:

• soit \(i=l-1\) et \(j=l-1\,\mbox{ ou }\,l\)

• soit \(i=l\) et \(j=l-1\,\mbox{ ou }\,l\)

Pour un élément \(\mathcal{P}^{1}\), on a donc à calculer uniquement 4 intégrales élémentaires sur un élément \(l\), que l’on peut écrire sous forme matricielle:

(4.12)\[\mathbf{K}_{pq}^{l}=\int_{x_{l-1}}^{x_{l}}K\frac{d}{dx}\phi_{l-2+q}(x)\frac{d}{dx}\phi_{l-2+p}(x)\;dx\,\mbox{ pour }\,p=1,2\,\,q=1,2\]

(4.13)\[\mathbf{M}_{pq}^{l}=\int_{x_{l-1}}^{x_{l}}K\phi_{l-2+p}(x)\phi_{l-2+q}(x)dx\,\mbox{ pour }\,p=1,2\,\,q=1,2\]

Avec ces notations, le premier élément de la matrice \(\mathbf{A}\) (4.12) s’écrit

\[\mathbf{A}_{11}=\mathbf{K}_{22}^{1}+\mathbf{M}_{22}^{1}+\mathbf{K}_{11}^{2}+\mathbf{M}_{11}^{2}\]

puisque le noeud 1 a pour support les éléments \([x_{0},x_{1}]\) (\(l=1\)) et \([x_{1},x_{2}]\) (\(l=2\) ). Par contre l’élément \(\mathbf{A}_{12}\) s’écrit:

\[\mathbf{A}_{12}=\mathbf{K}_{12}^{2}+\mathbf{M}_{12}^{2}\]

On a donc l’expression de \(\mathbf{A}\) sous la forme:

\[\begin{split}_{\mathbf{A}=\left[\begin{array}{ccc} \textcolor{red}{\mathbf{K}_{22}^{1}}+\textcolor{green}{\mathbf{K}_{11}^{2}} & \textcolor{green}{\mathbf{K}_{12}^{2}} & 0\\ \textcolor{green}{\mathbf{K}_{21}^{2}} & \textcolor{green}{\mathbf{K}_{22}^{2}}+\textcolor{blue}{\mathbf{K}_{11}^{3}} & \textcolor{blue}{\mathbf{K}_{12}^{3}}\\ 0 & \textcolor{blue}{\mathbf{K}_{21}^{3}} & \textcolor{blue}{\mathbf{K}_{22}^{3}} \end{array}\right]+\left[\begin{array}{ccc} \textcolor{red}{\mathbf{M}_{22}^{1}}+\textcolor{green}{\mathbf{M}_{11}^{2}} & \textcolor{green}{\mathbf{M}_{12}^{2}} & 0\\ \textcolor{green}{\mathbf{M}_{21}^{2}} & \textcolor{green}{\mathbf{M}_{22}^{2}}+\textcolor{blue}{\mathbf{M}_{11}^{3}} & \textcolor{blue}{\mathbf{M}_{12}^{3}}\\ 0 & \textcolor{blue}{\mathbf{M}_{21}^{3}} & \textcolor{blue}{\mathbf{M}_{22}^{3}} \end{array}\right]}\end{split}\]

Il reste donc à calculer ces matrices élémentaires pour calculer \(\mathbf{A}\). Pour ce faire on revient à la définition (4.7) des fonctions de base en fonction des fonctions de forme en effectuant le changement de variable (4.5) sur l’élément de référence. Sur un élément l \([x_{l-1},x_{l}]\) (de longueur \(h_{l}^ {}\)), on a:

(4.14)\[\phi_{l-1}(x)=N_1(\chi)=\chi\,\mbox{ et }\phi_{l}(x)=N_{2}(\chi)=1-\chi\]

En effectuant le changement de variables (4.5) dans l’intégrale, il vient:

\[\mathbf{K}_{pq}^{l}=h_{l}\int_{0}^{1}K(\frac{dN_{q}}{d\chi})\frac{1}{h_{l}}(\frac{dN_{p}}{d\chi})\frac{1}{h_{l}}d\chi\,\mbox{ et }\mathbf{M}_{pq}^{l}=h_{l}\int_{0}^{1}\alpha\,N_{p}N_{q}d\chi\]

Ces deux matrices élémentaires sont symétriques. De plus la somme des coefficients des lignes (et donc des colonnes) de \(\mathbf{K}^{l}\) est nulle parce que la somme des fonctions de forme \(N_{1}(\chi)+N_{2}(\chi)\) est égale à 1:

\[\begin{split}\begin{eqnarray} \mathbf{K}_{p1}^{l}+\mathbf{K}_{p2}^{l} & = & h_{l}\int_{0}^{1}K(\frac{dN_{1}}{d\chi})\frac{1}{h_{l}}(\frac{dN_{p}}{d\chi})\frac{1}{h_{l}}d\chi+h_{l}\int_{0}^{1}K(\frac{dN_{2}}{d\chi})\frac{1}{h_{l}}(\frac{dN_{p}}{d\chi})\frac{1}{h_{l}}d\chi\\ & = & h_{l}\int_{0}^{1}K(\frac{d}{d\chi}(N_{1}+N_{2})\frac{1}{h_{l}}(\frac{dN_{p}}{d\chi})\frac{1}{h_{l}}d\chi\\ & = & 0\end{eqnarray}\end{split}\]

Pour des coefficients \(K\) et \(\alpha\) constants, ces 2 matrices élémentaires s’écrivent, après le calcul simple des intégrales:

\[\begin{split}\mathbf{K}^{l}=\frac{K}{h_{l}}\left[\begin{array}{cc} 1 & -1\\ -1 & 1 \end{array}\right]\,\mbox{ et }\,\mathbf{M}^{l}=\alpha h_{l}\left[\begin{array}{cc} \frac{1}{3} & \frac{1}{6}\\ \frac{1}{6} & \frac{1}{3} \end{array}\right]\end{split}\]

En notant que les éléments du maillage ont les longueurs différentes: \(\textcolor{red}{h=\frac{L}{2}},\textcolor{green}{\,h_{2}=\frac{L}{4}},\,\textcolor{blue}{h_{3}=\frac{L}{4}}\), on obtiens la matrice A suivante en coloriant en rouge, vert et bleu les contributions des éléments 1,2 et 3:

\[\begin{split}\mathbf{A}=\frac{K}{L}\left[\begin{array}{ccc} \textcolor{red}{2}+\textcolor{green}{4} & \textcolor{green}{-4} & 0\\ \textcolor{green}{-4} & \textcolor{green}{4}+\textcolor{blue}{4} & \textcolor{blue}{-4}\\ 0 & \textcolor{blue}{-4} & \textcolor{blue}{4} \end{array}\right]+\alpha L\left[\begin{array}{ccc} \textcolor{red}{\frac{1}{6}}+\textcolor{green}{\frac{1}{12}} & \textcolor{green}{\frac{1}{24}} & 0\\ \textcolor{green}{\frac{1}{24}} & \textcolor{green}{\frac{1}{12}}+\textcolor{blue}{\frac{1}{12}} & \frac{1}{24}\\ 0 & \textcolor{blue}{\frac{1}{24}} & \textcolor{blue}{\frac{1}{12}} \end{array}\right]\end{split}\]

On vérifie la symétrie de la matrice.

4.1.5.2. assemblage du second membre

Le calcul du second membre procède de la même démarche. Le calcul des intégrales se fait élément par élément en tenant compte des propriétés des fonctions de base. L’expression du second membre \(\mathbf{B}\) de (4.9) contient 2 types de termes:

\[\mathbf{B}_{i}=\underbrace{\int_{0}^{L}\alpha T_{a}\phi_{i}dx}_{\mbox{terme source}}-\underbrace{\Phi_{e}\phi_{i}(L)}_{\mbox{cdt limite x=L}}-\underbrace{T_{e}\int_{0}^{L}(K\frac{d\phi_{0}}{dx}\frac{d\phi_{i}}{dx}+\alpha \phi_{0}\phi_{i})dx}_{\mbox{cdt limite x=0}}\]

1. un terme source à calculer sur tous les éléments

2. deux termes liés aux conditions aux limites en \(x=0\) et \(x=L\), que l’on ne calcule que pour certains éléments

Pour calculer le terme source, on le décompose en une somme d’intégrales élémentaires:

\[\int_{0}^{L}\alpha T_{a}\phi_{i}dx=\sum_{l=1}^{Ne}\int_{x_{l-1}}^{x_{l}}\alpha T_{a}\phi_{i}\,dx\]

et on utilise les propriétés des fonctions de base. Pour des éléments \(\mathcal{P}^{1}\), ces intégrales élémentaires sont non nulles uniquement si \(i=l-1\) ou \(i=l\) . On a donc à calculer 2 intégrales élémentaires par élément, qui s’écrivent sous forme d’un vecteur second membre élémentaire:

\[\mathbf{B}_{p}^{l}=\int_{x_{l-1}}^{x_{l}}\alpha T_{a}\phi_{l-2+p}dx\,\mbox{ pour }\,p=1,2\]

Avec cette notation, le terme source du second membre \(\mathbf{B}\) s’écrit:

\[\begin{split}\mathbf{B}=\left[\begin{array}{c} \textcolor{red}{B_{2}^{1}}+\textcolor{green}{B_{1}^{2}}\\ \textcolor{green}{B_{2}^{2}}+\textcolor{blue}{B_{3^ {}}^{1}}\\ \textcolor{blue}{B_{3}^{2}} \end{array}\right]+C.L.\end{split}\]

Pour le calcul du second membre élémentaire, on utilise le changement de variable (4.5) sur l’élément de référence. En utilisant la relation (4.13) , il vient:

\[\mathbf{B}_{p}^{l}=h_{l}\int_{0}^{1}\alpha T_{a}N_{p}d\chi\]

Si le coefficient \(\alpha\) et la température de l’air \(T_{a}\) sont constants, le second membre élémentaire s’écrit:

\[\begin{split}\mathbf{B}_{p}^{l}=\alpha T_{a}h_{l}\left[\begin{array}{c} \frac{1}{2}\\ \frac{1}{2} \end{array}\right]\end{split}\]

d’où la contribution du terme source dans le second membre \(\mathbf{B}\)

\[\begin{split}\mathbf{B}=\alpha T_{a}L\left[\begin{array}{c} \textcolor{red}{\frac{1}{4}}+\textcolor{green}{\frac{1}{8}}\\ \textcolor{green}{\frac{1}{8}}+\textcolor{blue}{\frac{1}{8}}\\ \textcolor{blue}{\frac{1}{8}} \end{array}\right]+C.L.\end{split}\]

La contribution des termes liés aux conditions aux limites n’interviens que sur certaines composantes de \(\mathbf{B}\). La contribution de la condition au limite en \(x=0\) fait intervenir le produit de la fonction de base \(N_{0}\) par une fonction de base \(N_{i}\). Comme il a été indiqué dans les propriétés des fonctions de base, ce produit est non nul uniquement pour \(i=1\) (on a donc uniquement une contribution dans \(\mathbf{B}_{1}\)) et l’intégrale se calcule sur l’élément \([x_{0},x_{1}]\):

\[T_{e}\int_{0}^{L}(K\frac{d\phi_{0}}{dx}\frac{d\phi_{1}}{dx}+\alpha \phi_{0}\phi_{1})dx=T_{e}\int_{x_{0}}^{x_{1}}(K\frac{d\phi_{0}}{dx}\frac{d\phi_{1}}{dx}+\alpha \phi_{0}\phi_{1})dx\]

Ce terme correspond justement aux intégrales élémentaires (4.12) et (4.13) pour l’élément \(0\) \([x_{0},x_{1}]\) multiplié par \(T_{e}\):

\[T_{e}\int_{0}^{L}(K\frac{d\phi_{0}}{dx}\frac{d\phi_{1}}{dx}+\alpha \phi_{0}\phi_{1})dx=(\mathbf{K}_{21}^{1}+\mathbf{M}_{21}^{1})T_{e}\]

La contribution de la condition aux limites en \(x=L\) fait intervenir \(\phi_{i}(L)\), qui est non nul uniquement pour \(i=3\). On a donc uniquement une contribution dans \(\mathbf{B}_{3}\) qui s’écrit:

\[\Phi_{e}\phi_{3}(L)=\Phi_{e}\]

Le second membre complet s’écrit alors:

(4.15)\[\begin{split}\mathbf{B}=\alpha T_{a}L\left[\begin{array}{c} \textcolor{red}{\frac{1}{4}}+\textcolor{green}{\frac{1}{8}}\\ \textcolor{green}{\frac{1}{8}}+\textcolor{blue}{\frac{1}{8}}\\ \textcolor{blue}{\frac{1}{8}} \end{array}\right]+\left[\begin{array}{c} -(\mathbf{K}_{21}^{1}+\mathbf{M}_{21}^{1})T_{e}\\ 0\\ -\Phi_{e} \end{array}\right]\end{split}\]

4.1.6. Résolution

Pour la résolution numérique, on considère un barreau d’aluminium de longueur \(L=3\,m\) , de diamètre \(d=2\,cm\), dont le coefficient de conductivité thermique vaut \(k=6000\,W/m/K\). Il est maintenu à une température \(T_{e}=60^{\circ}C\) en \(x=0\) et on impose un flux de \(\Phi_{e}=32\,W\) en \(x=L\). Il est refroidit dans l’air à température ambiante \(T_{a}=25^{\circ}C\) par convection forcée avec \(h=50\,W/m^{2}/K\) (pour de la convection naturelle \(h=10\,W/m^{2}/K\)).

Pour vérifier le calcul précédent, nous allons tout d’abord ne pas tenir compte de la convection (i.e. \(\alpha=0\)). Dans ce cas la solution exacte de l’équation (4.1) est triviale. La répartition de température est linéaire et vérifie:

\[T(x)=T_{e}+\frac{\Phi_{e}}{K}x\]

Le système linéaire discret s’écrit:

\[\begin{split}\left[\begin{array}{ccc} 376.99 & -251.33 & 0\\ -251.33 & 502.65 & -251.33\\ 0 & -251.33 & 251.33 \end{array}\right]\left[\begin{array}{c} T_{1}\\ T_{2}\\ T_{3} \end{array}\right]=\left[\begin{array}{c} 7539.82\\ 0\\ -32.00 \end{array}\right]\end{split}\]

ce qui donne après résolution la répartition de température:

\[\begin{split}\left[\begin{array}{c} T_{1}\\ T_{2}\\ T_{3} \end{array}\right]=\left[\begin{array}{c} 59.74\\ 59.61\\ 59.49 \end{array}\right]\end{split}\]

C’est exactement la solution analytique aux noeuds du maillage \((x=\frac{1}{2},\frac{3}{4},1)\). On constate que si la solution exacte est linéaire, la solution par éléments finis est égale à la solution exacte. Cela est naturelle, car l’approximation par élément finis \(\mathcal{P}^{1}\) approche exactement une solution linéaire. On note aussi que la variation de température dans la barre est très faible (de l’ordre \(0.5^{\circ}C\)), car le flux de chaleur en sortie \(\Phi_{e}\) est faible .

Dans le cas \(\alpha\ne0\) et avec des coefficients constants, on peut encore déterminer la solution analytique. Les calculs sont un peu plus complexes, et on donne le programme python ci dessous qui permet de calculer cette solution en utilisant la bibliothèque de calcul symbolique sympy.

import sympy as sp
import numpy as np
# variables symboliques
x = sp.symbols('x')
T = sp.Function('T')
K,alpha, L = sp.symbols('K alpha L',real=True,positive=True)
Ta, Te, Phi = sp.symbols('T_a T_e Phi',real=True)
# équation EDO
eq = sp.Eq(-K*T(x).diff(x,2)+alpha*T(x),alpha*Ta)
# solution symbolique
sol = sp.dsolve(eq,T(x),ics={T(0):Te,T(x).diff(x).subs(x,L):Phi/K}).simplify()
Tex = sol.rhs
# valeurs des paramètres
AN = { L: 3, K: 6000*np.pi*0.2**2/4., alpha: 50*np.pi*0.2, Ta:20, Te:60, Phi:-32 }
Te = Tex.subs(AN).simplify()
# trace solution exacte
sp.plot(Te,(x,0,3),title="solution exacte",ylabel="Te en °C",ylim=(40,60));

Avec ce programme, on obtiens l’expression analytique suivante:

\[ T_e(x) = \frac{\left(K^{\frac{3}{2}} \sqrt{\alpha} \left(- \sqrt{K} T_{a} \sqrt{\alpha} e^{\frac{L \sqrt{\alpha}}{\sqrt{K}}} + \sqrt{K} T_{e} \sqrt{\alpha} e^{\frac{L \sqrt{\alpha}}{\sqrt{K}}} - \Phi\right) e^{\frac{L \sqrt{\alpha}}{\sqrt{K}}} + \sqrt{K} \sqrt{\alpha} \left(- K^{\frac{3}{2}} T_{a} \sqrt{\alpha} + K^{\frac{3}{2}} T_{e} \sqrt{\alpha} + K \Phi e^{\frac{L \sqrt{\alpha}}{\sqrt{K}}}\right) e^{\frac{2 \sqrt{\alpha} x}{\sqrt{K}}} + K^{2} T_{a} \alpha \left(e^{\frac{2 L \sqrt{\alpha}}{\sqrt{K}}} + 1\right) e^{\frac{\sqrt{\alpha} x}{\sqrt{K}}}\right) e^{- \frac{\sqrt{\alpha} x}{\sqrt{K}}}}{K^{2} \alpha \left(e^{\frac{2 L \sqrt{\alpha}}{\sqrt{K}}} + 1\right)} \]

qui donne la solution suivante pour les valeurs numériques choisies

\[T_e(x)=20+3.066\,e^{0.4082x}+36.93\,e^{-0.4082x}\]

En remplaçant dans la matrice (4.13) et le second membre (4.15), on obtient le système suivant pour la solution numérique par éléments finis:

\[\begin{split}\left[\begin{array}{ccc} 400.56 & -247.40 & 0.0\\ -247.40 & 518.37 & -247.40\\ 0.0 & -247.40 & 259.18 \end{array}\right]\left[\begin{array}{c} T_{1}\\ T_{2}\\ T_{3} \end{array}\right]=\left[\begin{array}{c} 7775.44\\ 471.24\\ 203.62 \end{array}\right]\end{split}\]

ce qui donne après résolution la répartition de température:

\[\begin{split}\left[\begin{array}{c} T_{1}\\ T_{2}\\ T_{3} \end{array}\right]=\left[\begin{array}{c} 45.51\\ 42.26\\ 41.12 \end{array}\right]\end{split}\]

La solution analytique pour ces mêmes points de calcul vaut:

\[\begin{split}\left[\begin{array}{c} T_{1}\\ T_{2}\\ T_{3} \end{array}\right]=\left[\begin{array}{c} 45.67\\ 42.42\\ 41.28 \end{array}\right]\end{split}\]

La solution exacte étant de type exponentielle, l’approximation par éléments finis ne peut pas donner la solution exacte. On constate cependant que dans ce cas la solution élément finis est très précise, puisque l’erreur nodale est inférieure à \(0.1^{\circ}C\) (i.e. un écart relatif de \(\simeq0.4\%\) ).

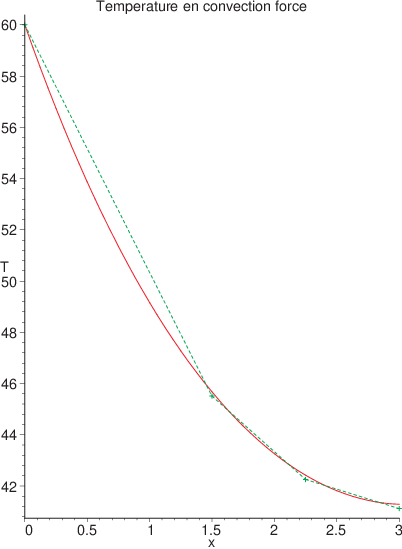
Fig. 4.9 Solution exacte (en rouge) et solution approchée (en bleu)

Quelques remarques:

1. Même si la solution par élément finis approche la solution exacte aux noeuds du maillage, entre les noeuds l’approximation est linéaire. Donc l’erreur entre la solution exacte et la solution élément finis peut être grande comme le montre la figure

2. Si on calcule la dérivée de la solution approchée, elle est constante par élément (voir la figure ci-dessus). On en déduit immédiatement que la condition au limite en \(x=L\) n’est pas vérifiée par la solution approchée:

\[-K\frac{dT^{h}}{dx}=-K\frac{T_{4}-T_{3}}{L/4}=285\ne\Phi_{e}=32\]

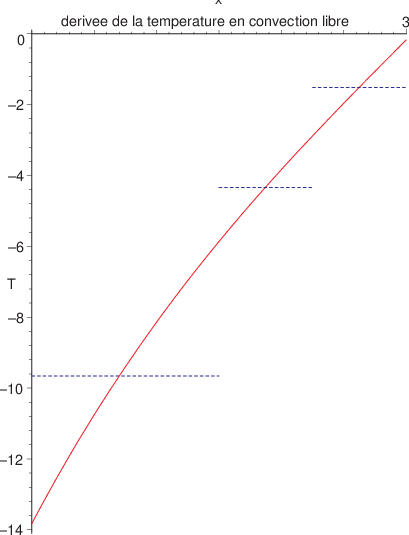
Fig. 4.10 Dérivée de la solution exacte (en rouge) et approchée (en bleu)

On montrera dans la suite que les conditions aux limites faibles sont vérifiées exactement par la solution approchée que lorsque le maillage devient très fin: i.e. à la limite quand la solution approchée tends vers la solution exacte.

4.2. Approximation par Éléments finis \(\mathcal{P}^{1}\)

Nous allons maintenant étudier l’approximation par éléments finis \(\mathcal{P}^{1}\) dans le cas général, en particulier ses propriétés en terme de précision et de convergence. Nous donnerons en même temps les programmes correspondants.

Pour cela nous allons traiter le cas d’une équation générique du type (4.1) sur le domaine \(\mathcal{D}=[0,L]\):

(4.16)\[\begin{split}\left\{ \begin{array}{c} -\frac{d}{dx}(K(x)\frac{d}{dx}u(x))+\alpha(x)u(x)=f(x)\\ u(0)=u_{e},\,\,-K(L)\frac{du}{dx}(L)=\beta u(L)+\phi_{0} \end{array}\right.\end{split}\]

Cette équation traduit un phénomène de diffusion de la solution \(u(x)\) avec un coefficient de diffusion \(K(x)\) variable, couplé à un terme source fonction de la solution \(u\) et d’un coefficient \(\alpha(x)\) variable. Le second membre \(f(x)\) traduit la partie du terme source indépendant de \(u\). En \(x=0\), on impose une condition de Dirichlet, et en \(x=L\) une condition de Fourier (ou condition mixte) qui impose que le flux de chaleur \(\Phi_{e}\)en \(x=L\) est une fonction de la solution \(u(L)\) (et non pas uniquement constant comme dans l’exemple précédent): \(\Phi_{e}=\beta u(L)+\phi_{0}\)

4.2.1. Formulation faible

Pour obtenir la formulation faible de (4.16), on procède comme précédemment. On multiplie l’équation (4.16) par une fonction test \(v(x)\), on intègre sur le domaine \(\mathcal{D}\), puis on effectue une intégration par partie sur les termes de plus haut degré. Il vient:

\[\int_{0}^{L}K(x)\frac{du}{dx}\,\frac{dv}{dx}\,dx-[K(x)\frac{du}{dx}v(x)]_{0}^{L}+\int_{0}^{L}\alpha(x)u(x)\,v(x)\,dx=\int_{0}^{L}f(x)v(x)\,dx\]

Le calcul du terme de bord se fait en utilisant les conditions aux limites et en imposant à la fonction test \(v(x)\) d’être une variation de la solution \(u(x)\). Comme on impose la valeur de \(u\) en \(x=0\) (\(u(0)=u_{e}\)), sa variation doit être nulle en ce point. La fonction test \(v\) doit donc s’annuler en \(x=0\). et le terme de bord \(K(0)\frac{du}{dx}(0)v(0)\) s’annule. Le second terme de bord se calcule à l’aide de la seconde condition aux limites: \(-K(K)\frac{du}{dx}(L)=\beta u(L)+\phi_{0}\). La formulation faible de (4.16) s’écrit alors:

(4.17)\[\begin{split}\left\{ \begin{array}{c} \mbox{Trouvez }u(x)\,\mbox{ avec }u(0)=u_{e}\mbox{ t.q.}\\ \int_{0}^{L}K(x)\frac{du}{dx}(x)\,\frac{dv}{dx}(x)\,dx+\int_{0}^{L}\alpha(x)u(x)\,v(x)\,dx+\beta u(L)v(L)=\\ \int_{0}^{L}f(x)v(x)\,dx-\phi_{0}v(L)\\ \mbox{ pour toute fonction test }v(x)\mbox{ vérifiant }v(0)=0 \end{array}\right.\end{split}\]

Exercice: montrez que cette formulation faible est équivalente à la formulation variationnelle suivante:

\[\begin{split}\left\{ \begin{array}{l} \mbox{Trouvez }u(x)\,\mbox{ avec }u(0)=u_{e}\mbox{ t.q.}\\ J(u)=\frac{1}{2}\int_{0}^{L}K(x)(\frac{du}{dx})^{2}\,dx+\frac{1}{2}\int_{0}^{L}\alpha(x)u(x)^{2}\,dx+\frac{1}{2}\beta u(L)^{2}-\int_{0}^{L}f(x)u(x)\,dx+\phi_{0}u(L)\\ \,\mbox{ soit minimum i.e. }J(u)\le J(w)\mbox{ pour toute fonction }w(x)\mbox{ avec }w(0)=u_{e} \end{array}\right.\end{split}\]

4.2.2. Approximation par éléments finis

Pour construire l’approximation par éléments finis \(\mathcal{P}^{1}\), on crée un maillage \(\mathcal{M}^{h}\) du domaine de calcul constitué de \(N_{e}\) segments de coordonnées \([x_{l},x_{l+1}]\):

\[\mathcal{M}^{h}=\bigcup_{l=1}^{Ne}[x_{l},x_{l+1}]\,\mbox{ avec }\,x_{1}=0,\,x_{Ne+1}=L\]

On note \(e_{l}=[x_{l},x_{l+1}]\), l’élément \(l\) du maillage de longueur \(h^{l}=x_{l+1}-x_{l}\). On choisit comme élément de référence le segment \([0,1]\).

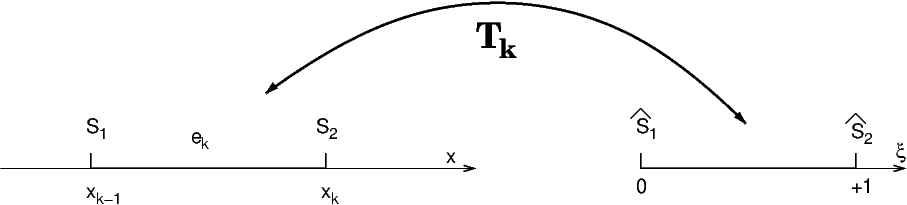
Fig. 4.11 élément finis $P^1

Remarques

1. on utilise l’élément de référence \([0,1]\) comme dans l’exemple précédent. La démarche est cependant indépendante du choix de cet élément de référence. On peut aussi choisir le segment \([-1,1]\), qui possède plus de propriétés de symétrie, et est donc un choix plus judicieux d’un point de vue algorithmique (en particulier pour les interpolations d’ordre plus élevées) .

2. on a choisit de numéroter les noeuds du maillage de 1 à \(N_{e}+1,\) contrairement à l’exemple précédent, où on les avait numéroté de 0 à \(N_{e}\). En effet dans certain langage de programmation (entre autre Maple et Matlab), les indices de tableaux commencent à 1 et non pas à 0. Là encore la démarche est indépendante de la numérotation des noeuds et des éléments.

3. D’autre part, contrairement au « calcul à la main » précédent, nous ne chercherons pas à éliminer la valeur au premier noeud de façon à conserver une approche générale.

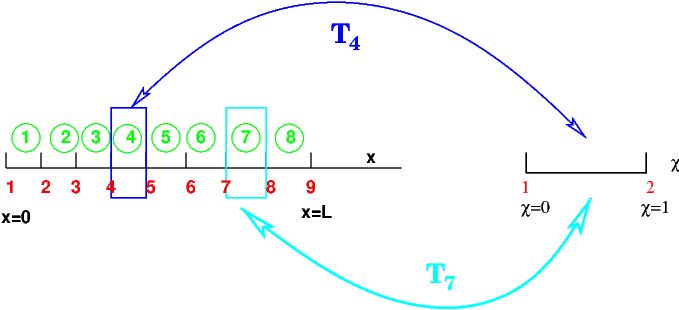
Fig. 4.12 maillage éléments finis et transformation vers l’élément de référence

Sur ce maillage, une approximation \(u^{h}(x)\) par éléments finis \(\mathcal{P}^{1}\) est définie par sa valeur \(u^{h}(x_{i})=u_{i}\) aux \(N_{e}+1\) points nodaux \(\{x_{i}\}_{i=1,N_e+1}\), correspondant aux extrémités des segments du maillage. Cette approximation possède donc \(N_n=N_e+1\) degré de liberté \(u_{i}\) correspondant aux \(N_n\) noeuds d’interpolation \(x_{i}\).

\[ u^h(x) = \sum_{i=1}^{N_n} u_i \phi_i(x) \]

Sur chaque élément cette approximation est définie à partir des 2 fonctions de forme \(N_1(\chi)\) et \(N_2(\chi)\) de l’élément \(\mathcal{P}^{1}\) (4.6) et du changement de variable \(\mathcal{F}^{l}(x)\) sur l’élément de référence (4.5):

\[\begin{split}\begin{eqnarray} u^{h}(x)&=&u_{l}N_{1}(\mathcal{F}^{l}(x))+u_{l+1}N_{2}(\mathcal{F}^{l}(x))\,\mbox{ pour }\,x\in e_{l}=[x_{l},x_{l+1}]\\ \mathcal{F}^{l}(x)&=&\frac{x-x_{l}}{x_{l+1}-x_{l}}\end{eqnarray}\end{split}\]

L’approximation globale est la somme de ces approximations élémentaires et s’écrit en fonction des fonctions de base \(\phi_{i}(x)\) :

\[u^{h}(x)=\sum_{i=1}^{Nn}u_{i}\phi_{i}(x)\]

Les fonctions de base \(\phi_{i}(x)\) sont définies à partir des deux fonction de forme \(N_1(\chi)\) et \(N_2(\chi)\) par les relations:

\[\begin{split}\begin{eqnarray} \phi_{i}(x)=N_{1}(\mathcal{F}^{i}(x)) & \mbox{ si } & x\in e_{i}\\ \phi_{i}(x)=N_{2}(\mathcal{F}^{i-1}(x)) & \mbox{ si } & x\in e_{i-1}\\ \phi_{i}(x)=0 & \mbox{ sinon} \end{eqnarray}\end{split}\]

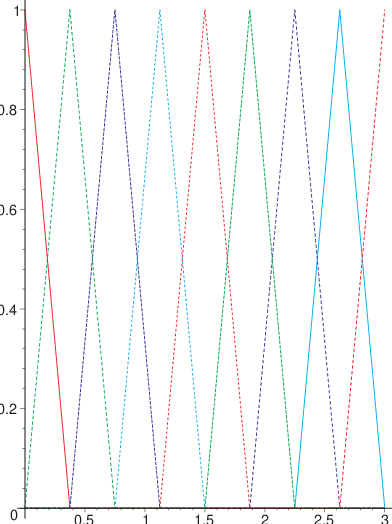
Fig. 4.13 Fonctions de base sur le maillage

Fig. 4.14 interpolation sur le maillage

Le programme Python suivant implémente cette interpolation éléments finis \(\mathcal{P}^{1}\) sur un maillage de \(N_{e}\) éléments.

import numpy as np
from scipy.interpolate import interp1d
# paramètre
L=3; Ne = 8
# maillage
h = L/Ne; Xp = np.linspace(0,L,Ne+1)
# longueur des elts
Nn = Nn = Ne+1
long = lambda k : Xp[k+1]-Xp[k]
# transformation xi(x) vers l'élément de référence [0,1]
xi = lambda chi,i: (1-chi)*Xp[i] + chi*Xp[i+1]

# ==========================
# interpolation P1 degre 1
d = 1
# pts d'interpolation
Xi = Xp[:]
# fonction forme P1 sur [-1,1]
N1 = interp1d([0,1],[1,0],kind=d)
N2 = interp1d([0,1],[0,1],kind=d)
# interpolation d'une fonction g sur un elts k
interpol = lambda chi,g,k : g(xi(0,k))*N1(chi)+g(xi(+1,k))*N2(chi)
# ==========================

# calcul de l'erreur d'interpolation
def Erreur(f):
    global Ne
    err = 0.
    XX = np.linspace(0,1,21)
    for k in range(Ne):
        h = long(k)
        Err = f(xi(XX,k)) - interpol(XX,f,k)
        err = err + np.trapz(Err**2,XX)*h
    return np.sqrt(err)

# application: test avec la fonction cos(2x)
f = lambda x : np.cos(2*x)
# tracer
plt.plot(Xi,f(Xi),'x--',label="interpolation")
XX = np.linspace(0,L,201)
plt.plot(XX,f(XX),label="cos(2x)")
plt.legend()
plt.title("Fonction et interpolation")
print("Erreur d'interpolation:",err)

Le programme est écrit de façon modulaire et générique, de telle sorte que l’on puisse très facilement implémenter une interpolation de degré \(p\) quelconque. Pour cela on introduit comme variable le degré \(p\) du polynôme d’interpolation, et on distingue les noeuds du maillage, que l’on note \(Xp\), des points d’interpolation, que l’on note \(Xi\). On introduit ensuite 2 fonctions: la fonction \(xi(\xi,k)\) qui fait la transformation de l’élément de référence vers l’élément \(k\) (i.e. calcul de \(x(\xi)\) , et la fonction long(l) qui calcul simplement la longueur \(h_{l}\) de l’élément \(l.\)

La partie propre à l’interpolation est entre les 2 lignes #======. On choisit le degré \(p\) d’interpolation. On y calcule les points d’interpolation, les fonctions de forme de l’élément \(\{N_p(x)\}_{p=0,k}\) qui sont les polynômes de Lagrange associés aux points d’interpolation sur l’élément de référence. On écrit ensuite une fonction \(Interpol(\chi,g,k)\) qui calcule la valeur en fonction de \(\chi\) (coordonnée sur l’élément de référence) de l’interpolation sur l’élément k de la fonction g

Pour une interpolation \(\mathcal{P}^2\) de degré 2, on modifie le code comme ci-dessous

# interpolation P2 de degré 2
d = 2
# pts d'interpolation
Xi = np.array([[Xp[k],(Xp[k]+Xp[k+1])/2.,Xp[k+1]] for k in range(Ne)]).flatten()
# fonction forme P2 sur [-1,1]
N1 = interp1d([0,0.5,1],[1,0,0],kind=d)
N2 = interp1d([0,0.5,1],[0,1,0],kind=d)
N3 = interp1d([0,0.5,1],[0,0,1],kind=d)
# interpolation d'une fonction g sur un elts k
interpol = lambda chi,g,k : g(xi(0,k))*N1(chi)+g(xi(0.5,k))*N2(chi)+g(xi(1.,k))*N3(chi)

Enfin on écrit une fonction \(Erreur(f)\) qui calcule la norme de l’erreur entre une fonction \(f(x)\) et son approximation \(f^{h}\) sur le maillage élément finis. On choisit comme norme, l’intégrale du carré de la différence (norme \(L^{2}\)):

\[\Vert f-f^{h}\Vert^{2}=\int_{0}^{L}(f(x)-f^{h}(x))^{2}\,dx\]

Cette norme mesure l’erreur moyenne sur le domaine de calcul. Pour cela on calcule l’intégrale élément par élément, en notant que sur chaque élément, la fonction \(f^{h}\) s’écrit en utilisant les fonctions de forme de l’élément ainsi que les valeurs nodales de \(f^{h}\). Pour une approximation \(\mathcal{P}^{1}\) sur un élément \(l\) \([x_{l},x_{l+1}]\), on a:

\[f^{h}(x)=F[l]\,N_{1}(Fr(x))+F[l+1]\,N_{2}(Fr(x))\]

ce qui donne pour l’erreur:

\[\Vert f-f^{h}\Vert^{2}=\sum_{l=1}^{Ne}\int_{x_{l}}^{x_{l+1}}(f(x)-(F[l]\,N_{1}(Fr(x))+F[l+1]\,N_{2}(Fr(x)))^{2}dx\]

Dans ce programme Python, on a utilisé les fonctions de la bibliothéque numpy et scipy pour calculer l’interpolation de Lagrange interp1d en fonction du degré \(d\) d’interpolation et la fonction fonction trapz pour faire l’intégration numérique de l’erreur sur l’élément de référence.

La fin du programme est un exemple d’interpolation d’une fonction \(f(x)=sin(2x)\) sur un maillage de 10 éléments de \([0,3].\) Les fonctions de base et l’interpolation sont données sur la figure. L’erreur d’interpolation vaut dans ce cas:\(\Vert f-f^{h}\Vert=0.039\). En utilisant une interpolation \(\mathcal{P}^2\) (avec le même programme modifié) l’erreur diminue d’un facteur 10 et vaux \(\Vert f-f^{h}\Vert=0.003\)

4.2.3. Formulation faible discrète

La solution approchée \(u^{h}\) par éléments finis \(\mathcal{P}^{1}\) de (4.15) s’écrit sous la forme:

\[u^{h}(x)=\sum_{i=1}^{Nn}u_{i}N_{i}(x)\]

Elle doit vérifier les conditions aux limites fortes ( i.e. la condition de Dirichlet en \(x=0\) : \(u^{h}(0)=u_{e}\)). En notant à nouveau que les fonctions de bases vérifient \(N_{i}(x_{j})=\delta_{ij}\), cette condition impose la valeur nodale de \(u^{h}\) au noeud \(x_{1}=0\) du maillage:

(4.18)\[u^{h}(x)=\sum_{j=1}^{Nn}u_{j}N_{j}(x)\,\mbox{ avec }\,u_{1}=u_{e}\]

Les fonctions tests associées \(v^{h}\) étant des variations de \(u^{h}\), elles doivent donc s’annuller en \(x=0\). Elles s’écrivent sous la forme générale suivante:

(4.19)\[v^{h}(x)=\sum_{i=1}^{Nn}v_{i}N_{i}(x)\,\mbox{ avec }v_{1}=0\]

Ces fonctions tests sont des combinaisons linéaires des \(Nn-1\) fonctions de base \(\{N_{i}(x)\}_{i=2,Nn}\). En remplaçant dans la formulation faible (4.15) la solution exacte \(u\) par la solution approchée \(u^{h}\) donnée par (4.19) et la fonction test \(v\) par une de ces \(Nn-1\) fonctions de base \(\{N_{i}(x)\}_{i=2,Nn}\) , on obtiens la formulation faible discrète:

(4.20)\[\begin{split}\begin{aligned} \sum_{j=1}^{Nn}u_{j}\left(\int_{0}^{L}K(x)\frac{dN_{j}}{dx}(x)\,\frac{dN_{i}}{dx}(x)\,dx+\int_{0}^{L}\alpha(x)N_{j}(x)\,N_{i}(x)\,dx\right)+\underbrace{\beta u_{Nn}N_{i}(L)}_{\mbox{terme C.L sur A.}} & = \\ \int_{0}^{L}f(x)N_{i}(x)\,dx-\underbrace{\phi_{0}N_{i}(L)}_{\mbox{terme C.L. sur B}}\end{aligned}\end{split}\]

Pour obtenir cette relation on a permuté la sommation \(\sum_{i=1}^{Nn}\) et l’intégration \(\int_{0}^{L}\) et on a sortie les coefficients \(u_{i}\) des intégrales. D’autre part on a remplacé \(u^{h}(L)\) par sa valeur \(u_{Nn}\). L’équation (4.20) écrite pour \(i=2,Nn\) est un système linéaire de \(Nn-1\) inconnues \(\{u_{i}\}_{i=2,Nn}\) (en notant que \(u_{1}=u_{e}\) est fixé par la condition aux limites), qu’il suffit de résoudre pour obtenir la solution approchée \(u^{h}\). De façon à construire un programme le plus général possible, on considérera que l’on a \(Nn\) inconnues \(u_{i}\), qui sont données par les \(Nn-1\) équations (4.20) auxquelles on ajoute l’équation supplémentaire \(u_{1}=u_{e}\). Dans cette approche on construit un système linéaire de \(Nn\) inconnues à \(Nn\) équations. Dans un premier temps cela permettra de construire la matrice \(\mathbf{A}\) et le second membre \(\mathbf{B}\) du système linéaire sans tenir compte des conditions aux limites et donc de façon générique. Puis dans un second temps, on appliquera les conditions aux limites sur le système linéaire: i.e. on remplacera la première équation par l’équation \(u_{1}=u_{e}\) et on introduira le terme lié à la conditions aux limites en \(x=L\)

Les coefficients génériques de \(\mathbf{A}\) et de \(\mathbf{B}\) s’écrivent:

\[\begin{split}\begin{eqnarray} \mathbf{A}_{ij} & = & \int_{0}^{L}K(x)\frac{dN_{j}}{dx}(x)\,\frac{dN_{i}}{dx}(x)\,dx+\int_{0}^{L}\alpha(x)N_{j}(x)\,N_{i}(x)\,dx\\ \mathbf{B}_{i} & = & \int_{0}^{L}f(x)N_{i}(x)\,dx \end{eqnarray}\end{split}\]

Pour calculer ces coefficients, on effectue un calcul élément par élément en déterminant les matrices élémentaires et les second membres élémentaires sur un élément \(e_{l}\) . Pour cela on calcul tout d’abord une interpolation \(K^{h}(x),\,\alpha^{h}(x),\,f^{h}(x)\) des coefficients \(K(x)\), \(\alpha(x)\) et du second membre \(f(x)\) sur le maillage éléments finis:

\[K^{h}(x)=\sum_{i=1}^{Nn}K_{i}\,N_{i}(x),\,\,\alpha^{h}(x)=\sum_{i=1}^{Nn}\alpha_{i}N_{i}(x)\,\,f^{h}(x)=\sum_{i=1}^{Nn}f_{i}N_{i}(x)\]

Une autre approche consisterait à calculer une approximation éléments finis de ces coefficients sur chaque élément, ou à choisir une valeur moyenne par élément.

Exercice: comparer le calcul de la matrice élémentaire de raideur avec une approximation de \(K(x)\) constante, \(\mathcal{P}^{1}\) et exacte dans le cas où \(K(x)\) est un polynôme de degré 1 et 2

4.2.4. Matrice élémentaire

Sur un élément \(l\) la matrice élémentaire est la somme d’une matrice de rigidité \(\mathbf{K}^{l}\) et d’une matrice de masse \(\mathbf{M}^{l}\), qui pour des éléments finis de degré \(d\) sont des matrices \((d+1,d+1)\) puisque le nombre de points d’interpolation pour un polynôme de degré \(d\) est en \(d+1\). Sur un élément, on a \(d+1\) fonctions de forme \(\{N_{p}(\chi)\}_{p=1,d+1}\) et on note \(\{n_{i}\}_{i=1,d+1}\) les numéros des points d’interpolation sur l’élément.

Pour un élément \(\mathcal{P}^{1}\), on a \(d=1\) et:

\[N_{1}(\chi)=1-\chi,\,\,N_{2}(\chi)=\chi\,\,,n_{1}=l,\,\,n_{2}=l+1\]

Avec ces notations, de façon générique (i.e. valable pour un approximation \(\mathcal{P}^{1}\), \(\mathcal{P}^{2}\),\(\ldots\) \(\mathcal{P}^{d}\)), les coefficient \(K(x)\) et \(\alpha(x)\) peuvent s’écrire sur un élément \(l\):

\[K^{h}(x)=\sum_{i=1}^{d+1}K_{n_{i}}N_{i}(\chi)\;,\; \alpha^{h}(x)=\sum_{i=1}^{d+1}\alpha_{n_{i}}N_{i}(\chi)\]

et les matrices élémentaires s’écrivent:

(4.21)\[\mathbf{K}_{pq}^{l}=\sum_{i=1}^{d+1}K_{n_{i}}\frac{1}{h^{l}}\int_{0}^{1}N_{i}(\chi)\frac{dN_{p}}{d\chi}(\chi)\,\frac{dN_{q}}{d\chi}(\chi)\,d\chi\,\,\,(\,p=1,d+1,\,q=1,d+1)\]

(4.22)\[\mathbf{M}_{pq}^{l}=\sum_{i=1}^{d+1}\alpha_{n_{i}}h^{l}\int_{0}^{1}N_{i}(\chi)N_{p}(\chi)\,N_{q}(\chi)\,d\chi\,\,\,(\,p=1,d+1,\,q=1,d+1)\]

Le programme MatRigidite ci-dessous implémente le calcul de la matrice de rigidité, en programmant la relation (4.21) comme une fonction, en utilisant une intégration symbolique des fonctions de formes:

def MatRigidite(h,K):
	"""h taille elt, K valeurs nodales de K(x) sur l'elt"""
    global d,N
    Ke = sp.zeros(d+1,d+1)
    # interpolation du coeff K
    Kh = sp.S(0)   
    for i in range(d+1):
        Kh += K[i]*N[i](x)
    # matrice élémentaire
    for p in range(d+1):
        dNp = N[p](x).diff(x)
        for q in range(d+1):
            dNq = N[q](x).diff(x)
            Ke[p,q] = sp.integrate(Kh*dNp*dNq,(x,0,1))/h
    return Ke

En définissant les fonctions de formes de façon symboliques dans le tableau \(N\),

# fonction de forme P1
d=1
N = [ sp.Lambda(x,1-x), sp.Lambda(x,x)]

Si la fonction \(K(x)=K\) est constante, on retrouve pour des éléments \(\mathcal{P}^{1}\) la matrice élémentaire classique suivante avec le code python suivant:

# matrice de rigidité cas K=cste
h,K = sp.symbols('h K')
MatRigidite(h,[K,K])

\[\begin{split} \mathbf{K}^{k}=\frac{K}{h}\left[\begin{array}{cc} 1 & -1\\ -1 & 1\end{array}\right] \end{split}\]

Dans le cas général, pour un maillage de \(8\) éléments \(P^{1}\), on obtiens pour l’élément \(4\) (\([x_{4},x_{5}]\)):

\[\begin{split}\mathbf{K}^{4}=\left[\begin{array}{cc} 4/3\,K_{{4}}+4/3\,K_{{5}} & -4/3\,K_{{4}}-4/3\,K_{{5}}\\ -4/3\,K_{{4}}-4/3\,K_{{5}} & 4/3\,K_{{4}}+4/3\,K_{{5}} \end{array}\right]\end{split}\]

De même le programme ci-dessous implémente le calcul de la matrice de masse, en programmant la relation (4.22).

def MatMasse(h,Alpha):
	"""h taille elt, Alpha valeurs nodales de alpha(x) sur l'elt"""
    global d
    Me = sp.zeros(d+1,d+1)
    # interpolation du coeff alpha
    Ah = sp.S(0)    
    for i in range(d+1):
        Ah += Alpha[i]*N[i](x)
    # matrice élémentaire
    for p in range(d+1):
        Np = N[p](x)
        for q in range(d+1):
            Nq = N[q](x)
            Me[p,q] = sp.integrate(Ah*Np*Nq,(x,0,1))*h
    return Me

Si la fonction \(\alpha(x)\) est constante, on retrouve pour des éléments \(\mathcal{P}^{1}\) la matrice élémentaire classique suivante avec le code python suivant:

MatMasse(h,[alpha,alpha])

\[\begin{split} \mathbf{M}^{k}=\alpha h\left[\begin{array}{cc} 1/3 & 1/6\\ 1/6 & 1/3\end{array}\right] \end{split}\]

Dans le cas général et pour le même cas que précédemment, on obtiens:

\[\begin{split}\mathbf{M}^{4}=\left[\begin{array}{cc} 3/32\,\alpha_{{4}}+1/32\,\alpha_{{5}} & 1/32\,\alpha_{{4}}+1/32\,\alpha_{{5}}\\ 1/32\,\alpha_{{4}}+1/32\,\alpha_{{5}} & 1/32\,\alpha_{{4}}+3/32\,\alpha_{{5}} \end{array}\right]\end{split}\]

4.2.5. Second membre élémentaire

Le calcul du second membre élémentaire procède de la même démarche. Après approximation de \(f(x)\) sur l’élément, il vient:

(4.23)\[\mathbf{B}_{p}^{l}=\sum_{i=1}^{d+1}f_{n_{i}}\,\int_{0}^{1}N_{i}(\chi)N_{p}(\chi)d\chi\,\mbox{ pour }\,p=1,d+1\]

Le programme ci-dessous implémente le calcul de ce vecteur élémentaire, en programmant la relation (4.23)

def SmbElem(h,F):
    """h taille elt, F valeurs nodales de F(x) sur l'elt"""
    global d
    Be = sp.zeros(1,d+1)
    # interpolation du coeff alpha
    Fh = sp.S(0)    
    for i in range(d+1):
        Fh += F[i]*N[i](x)
    # second membre elementaire
    for p in range(d+1):
        Np = N[p](x)
        Be[p] = sp.integrate(Fh*Np,(x,0,1))*h
    return Be

Dans le cas d’une approximation \emph{\(\mathcal{P}^{1}\)}, on trouve l’expression, avec le avec le code python suivant:

Fk,Fk1 = sp.symbols("F_k F_{k+1}")
SmbElem(h,[Fk,Fk1])

\[\begin{split} \mathbf{B}^{k}=\frac{h}{6}\left[\begin{array}{c} 2f_{k}+f_{k+1}\\ f_{k}+2f_{k+1}\end{array}\right] \end{split}\]

Exercice: démontrer cette dernière relation.

Dans le cas général et pour le même cas que précédemment, on obtiens:

\[\mathbf{B}^{4}=[1/8\,f_{{5}}+1/16\,f_{{6}},1/16\,f_{{5}}+1/8\,f_{{6}}]\]

4.2.6. Assemblage

Le calcul de la matrice globale \(\mathbf{A}\) et du second membre \(\mathbf{B}\) s’effectue par une procédure générique d’assemblage, qui calcule les matrices élémentaires élément par élément et ensuite insère les coefficients de ces matrices à la bonne place dans la matrice globale.

Ainsi pour un élément \(l\) de degré \(d\) dont les numéros des noeuds d’interpolation sont notés \(\{n_{i}\}_{i=1,d+1}\), la matrice élémentaire \(\mathbf{A}^{l}\) de dimension \((d+1,d+1)\) à des contributions dans la matrice globale \(\mathbf{A}\) de dimension \((Nn,Nn)\). Plus précisément le coefficient \((p,q)\) de la matrice élémentaire \(\mathbf{A}^{l}\) intervient dans le calcul du coefficient \((n_{p},n_{q})\) de la matrice globale \(\mathbf{A}\), puisque \(n_{p}\) est le numéro global du point d’interpolation \(p\) de l’élément \(l,\) et \(n_{q}\) le numéro global du point d’interpolation \(q\) de l’élément .

\[\mathbf{A}_{n_{p},n_{q}}=\mathbf{A}_{n_{p},n_{q}}+\mathbf{A}_{p,q}^{l}\]

Pour un élément \(e_{k}\) de type \(\mathcal{P}^{1}\) ayant comme numéro de sommets \(\{ n_{1},n_{2}\}\), la matrice élémentaire \(\mathbf{A}^{k}\) de dimension \((2,2)\) contribue aux coefficients de la matrice globale \(\textbf{A}\) suivants:

\[\begin{eqnarray*} A_{n_{1},n_{1}}\leftarrow\, A_{n_{1},n_{1}}+A_{1,1}^{k}\,\,\,, & A_{n_{1},n_{2}}\leftarrow\, A_{n_{1},n_{2}}+A_{1,2}^{k}\\ A_{n_{2},n_{1}}\leftarrow\, A_{n_{2},n_{1}}+A_{2,1}^{k}\,\,\,, & A_{n_{2},n_{2}}\leftarrow\, A_{n_{2},n_{2}}+A_{2,2}^{k} \end{eqnarray*}\]

Par exemple, sur le maillage de la figure précédente, la matrice élémentaire \(\mathbf{A}^{4}\)sur l’élément \(4\) contribue aux 4 coefficients suivants de \(\mathbf{A}\):

\[\mathbf{A}_{4,4}=\mathbf{A}_{4,4}+\mathbf{A}_{0,0}^{4},\,\,\mathbf{A}_{4,5}=\mathbf{A}_{4,5}+\mathbf{A}_{0,1}^{4},\]

\[\mathbf{A}_{5,4}=\mathbf{A}_{5,4}+\mathbf{A}_{1,0}^{4},\,\,\mathbf{A}_{5,5}=\mathbf{A}_{5,5}+\mathbf{A}_{1,1}^{4}\]

L’algorithme d’assemblage général est donnée ci dessous:

Algorithm 4.1 (Algorithme d’assemblage)

1. d = 1 // dimension interpolation)

2. A = 0 // matrice

3. B = 0 // second membre

4. Pour k de 1 à Ne faire

   1. h = long(k) // taille élément

   2. noi = num(k) // liste des numéros des noeuds de l’elt

   3. Ke = MatRigidite(h,K) // calcul des matrices élémentaires

   4. Me = MatMasse(h,alpha)

   5. Be = SmbElem(h,K)

   6. Pour p de 1 à d+1 faire

      1. ni = noi[p]

      2. Pour q de 1 à d+1 faire

         1. nj = noi[q]

         2. A[ni,nj] = A[ni,nj] + Ke[p,q] + Me[p,q] // assemblage matrice

      3. Fin q

      4. B[ni] = B[ni] + Be[p] // assemblage second membre

   7. Fin p // boucle sur les nds de l’elt

5. Fin k // boucle sur les elts

A l’issue de cet assemblage la matrice \(\mathbf{A}\) et le second membre \(\mathbf{B}\) calculée avec les paramètres de l’exemple précédent

\[L=3\,m,\,\,p=2\,cm,\,\,h=50\,W/m^{2}/K,\,k=6000\,W/m/K,\,T_{e}=60\,C,\,T_{a}=20\,C,\,\Phi_{e}=32\,W\]

s’écrivent pour un maillage de \(N_{e}=8\) éléments:

\[\begin{split}\mathbf{A}=\left[\begin{array}{ccccccccc} 507.0 & -501.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0\\ -501.0 & 1010.0 & -501.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0\\ 0.0 & -501.0 & 1010.0 & -501.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0\\ 0.0 & 0.0 & -501.0 & 1010.0 & -501.0 & 0.0 & 0.0 & 0.0 & 0.0\\ 0.0 & 0.0 & 0.0 & -501.0 & 1010.0 & -501.0 & 0.0 & 0.0 & 0.0\\ 0.0 & 0.0 & 0.0 & 0.0 & -501.0 & 1010.0 & -501.0 & 0.0 & 0.0\\ 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & -501.0 & 1010.0 & -501.0 & 0.0\\ 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & -501.0 & 1010.0 & -501.0\\ 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & -501.0 & 507.0 \end{array}\right]\end{split}\]

\[\mathbf{B}=[118.0,236.0,236.0,236.0,236.0,236.0,236.0,236.0,118.0]\]

Cette matrice est symétrique et tri diagonale (car avec l’interpolation \(\mathcal{P}^{1}\), une fonction de base associée à un noeud ou degré de liberté \(x_{i}\) est non nulle sur l’intervalle \([x_{i-1},x_{i+1}]\)).

4.2.7. Prise en compte des conditions aux limites

Le calcul précédent est générique et ne tiens pas compte des conditions aux limites. Pour la condition aux limites de Dirichlet en \(x=0\), on remplace la première équation par la condition:

\[T_{1}=T_{e}\]

ce qui reviens à annuler la première ligne de la matrice \(\mathbf{A}\), puis à mettre un 1 sur le terme diagonale \(\mathbf{A}_{11}\), et \(T_{e}\) dans \(\mathbf{B}_{11}\). Pour la condition aux limites en \(x=L\) (condition mixte), il faut rajouter un terme dans la matrice \(\mathbf{A}\) correspondant à :

\[\beta u_{Nn}\phi_{i}(L)=\beta\,\delta_{i,Nn}\,u_{Nn}\]

qui est non nul uniquement pour \(i=Nn\). Il faut donc modifier uniquement le terme diagonale \(\mathbf{A}_{Nn,Nn}\):

\[\mathbf{A}_{Nn,Nn}\leftarrow\mathbf{A}_{Nn,Nn}+\beta\]

Pour le second membre \(\mathbf{B}\), il faut rajouter le terme

\[-\phi_{0}\phi_{i}(L)=-\phi_{0}\delta_{i,Nn}\]

qui est non nul uniquement pour \(i=Nn\). Il faut donc modifier uniquement le dernier terme de \(\mathbf{B}:\)

\[\mathbf{B}_{Nn}\leftarrow\mathbf{B}_{Nn}-\phi_{0}\]

Le calcul de la solution se fait en résolvant le système linéaire ainsi construit. La matrice \(\mathbf{A}\) s’écrit:

\[\begin{split}\mathbf{A}=\left[\begin{array}{ccccccccc} 1.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0\\ -501.0 & 1010.0 & -501.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0\\ 0.0 & -501.0 & 1010.0 & -501.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0\\ 0.0 & 0.0 & -501.0 & 1010.0 & -501.0 & 0.0 & 0.0 & 0.0 & 0.0\\ 0.0 & 0.0 & 0.0 & -501.0 & 1010.0 & -501.0 & 0.0 & 0.0 & 0.0\\ 0.0 & 0.0 & 0.0 & 0.0 & -501.0 & 1010.0 & -501.0 & 0.0 & 0.0\\ 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & -501.0 & 1010.0 & -501.0 & 0.0\\ 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & -501.0 & 1010.0 & -501.0\\ 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & -501.0 & 507.0 \end{array}\right]\end{split}\]

et le second membre \(\mathbf{B}\):

\[\mathbf{B}=[60.0,236.0,236.0,236.0,236.0,236.0,236.0,236.0,85.8]\]

On constate que la matrice \(A\) n’est plus symétrique, à cause de la façon d’implémenter la condition aux limites de Dirichlet. Nous verrons dans le chapitre suivant comment imposer cette condition en conservant la symétrie.

4.2.8. Résultats

Avec les paramètres numériques précédents et un maillage de \(8\) éléments la solution obtenue vaut.

\[\mathbf{X}=[60.0,55.3,51.3,48.2,45.7,43.8,42.4,41.6,41.3]\]

La comparaison de cette solution éléments finis avec la solution exacte est donnée sur la figure suivant.

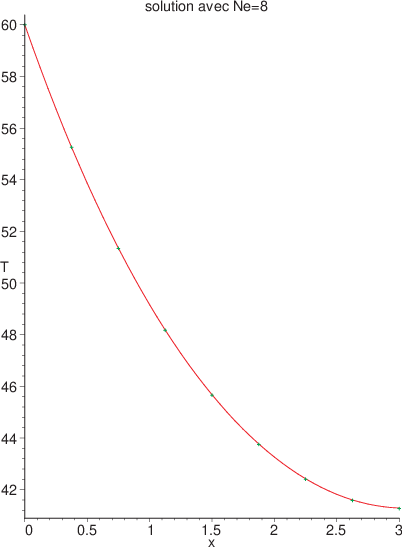
Fig. 4.15 Solution éléments finis pour Ne=32

On constate que l’erreur moyenne est très faible et vaut \(0.083\) (soit \(0.1\%\) en relatif), mais l’approximation de la dérivée en \(x=L\) reste encore assez mauvaise: on trouve \(158\) au lieu de \(32\) (soit \(390\,\%\) d’erreur), ce qui est cependant meilleur qu’avec 3 éléments où on obtiens \(374\). A titre de comparaison, avec le maillage de 3 éléments non régulièrement espacés du paragraphe 3.1, la solution est meilleure puisque l’on trouve un flux de \(285\). On intuite ici l’intérêt en élément finis d’utiliser des maillages non réguliers.

4.2.9. Etude de la précision

Pour étudier la précision de la méthode des éléments finis \(\mathcal{P}^{1}\), nous avons calculer l’erreur relative moyenne \(\frac{||u-u^{h}||}{||u||}\) et l’erreur relative sur la condition aux limites en \(x=L\) en fonction du nombre d’éléments \(Ne\) du maillage. Les résultats sont tracés en échelle logarithmique sur la figure suivante. On constate que l’erreur relative moyenne varie en \(\frac{1}{Ne^{2}}\) (comparaison avec une droite de pente \(-2\)), et que l’erreur relative sur la condition aux limites varie en \(\frac{1}{Ne}\). Ce résultat montre que l’approximation par éléments finis \(u^{h}\) converge vers la solution exacte et que cette convergence est d’ordre 2. Ce résultat est cohérent avec l’erreur d’interpolation, qui est d’ordre 2 pour une approximation \(\mathcal{P}^{1}\). On peut en fait démontrer que l’erreur par éléments finis est majoré par cette erreur d’interpolation.

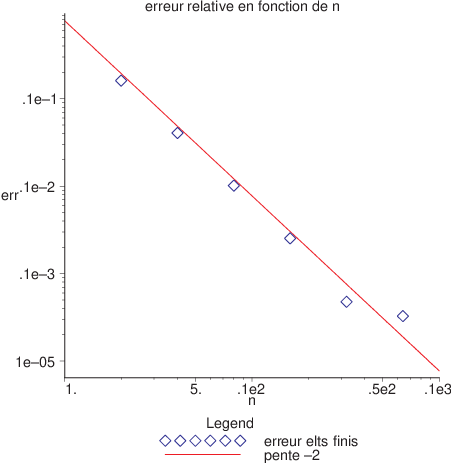
Fig. 4.16 Erreur relative en fonction de Ne(elt P1)

4.3. Approximation par Éléments finis \(\mathcal{P}^{2}\)

L’approximation par éléments finis \(\mathcal{P}^{2}\) consiste à utiliser une interpolation polynomiale de degré 2 sur l’élément de référence \(\hat{e}\). On utilise les 3 points d’interpolations \(\hat{S}_{1}\) \((\xi=0)\), \(\hat{S}_{2}\) \((\xi=1/2)\), \(\hat{S}_{3}\) \((\xi=1)\) sur \(\hat{e}\) associés à 3 points sur l’élément \(e_{k}\) : les 2 extrémités du segment \(S_{1}\), \(S_{3}\) , et le milieu du segment \(S_{2}\). On notera \(\{ n_{1},n_{2},n_{3}\}\) les numéros de ces 3 noeuds.

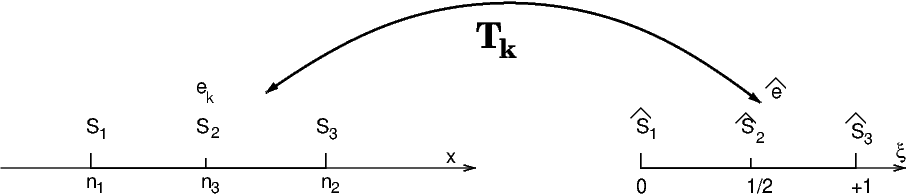
Fig. 4.17 éléments finis \(P^2\)

Sur l’élément de référence, on définit donc 3 fonctions de formes:

\[ N_{1}(\xi)=2(\xi-1)(\xi-\frac{1}{2}),\, N_{2}(\xi)=4\xi(1-\xi),\, N_{3}(\xi)=2\xi(\xi-\frac{1}{2}) \]

qui sont tracées sur la figure ci dessous:

Fig. 4.18 Fonctions de forme \(P^2\)

4.3.1. Interpolation \(P^{2}\)

Pour une approximation par éléments finis \(P^{2}\), un maillage de \(N_{e}\) éléments correspond à \(2N_{e}+1=Nn\) points nodaux, puisque sur chaque élément \(l\), on définit 3 points d’interpolations: les 2 extrémités du segment et le milieu de l’élément. Le programme ci dessous implémente l’interpolation \(P^{2}\).

# degre interpolation et pt
d = 2
# pts d'interpolation
Xi = np.array([[Xp[k],(Xp[k]+Xp[k+1])/2.,Xp[k+1]] for k in range(Ne)]).flatten()
# fonction forme P1 sur [0,1]
N1 = interp1d([0,0.5,1],[1,0,0],kind=d)
N2 = interp1d([0,0.5,1],[0,1,0],kind=d)
N3 = interp1d([0,0.5,1],[0,0,1],kind=d)
# interpolation d'une fonction g sur un elts k
interpol = lambda chi,g,k : g(xi(0,k))*N1(chi)+g(xi(0.5,k))*N2(chi)+g(xi(1.,k))*N3(chi)

Dans ce programme, les \(Ne+1\) points du maillage sont notés Xp, alors que les \(2N_{e}+1\) points nodaux (i.e. degré de liberté) sont notés Xi et sont calculés en fonction de Xp . La numérotation des 3 points d’interpolation pour un élément \(l\) est donnée par la fonction num . Les 3 fonctions de forme sont calculées comme polynômes de Lagrange avec le changement de variable vers l’élément de référence, et la fonction d’interpolation (ce sont les mêmes que pour l’interpolation \(P^{1})\). Par contre le calcul de l’erreur moyenne d’interpolation est différente de la fonction \(P^{1}\), puisque l’on fait explicitement intervenir les fonctions de forme par élément.

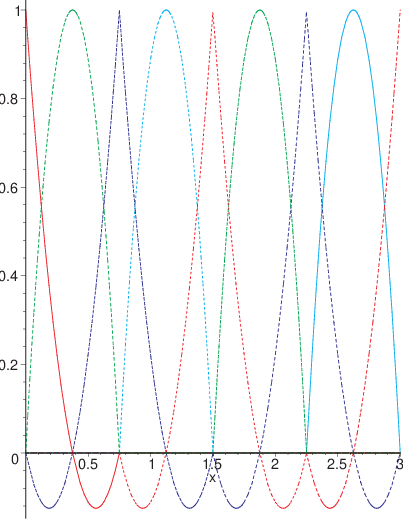
Fig. 4.19 Fonctions de base et interpolation \(P^{2}\) sur un maillage \(Ne=5\)

Les fonctions de base pour un maillage avec \(Ne=5\) éléments (et donc le même nombre de degré de liberté \(Nn=11\) que dans l’exemple \(P^{1}\)) sont tracées sur les figures précédentes, ainsi que l’interpolation \(P^{2}\) de la fonction \(f(x)=cos(2x)\) , que l’on comparera avec l’interpolation \(P^{1}\) sur un maillage identique. On constate que l’approximation \(P^{2}\) est meilleure que l’approximation \(P^{1}\), ce qui est confirmée par la valeur de l’erreur moyenne:\(\Vert f-f^{h}\Vert=0.012\) (soit plus de 3 fois plus faible).

4.3.2. Approximation par éléments finis \(P^{2}\)

Pour le calcul des matrices élémentaires, on utilise les fonctions précédentes en définissant simplement les fonctions de forme \(P^2\) de façon symbolique.

# fonction de forme P2
d = 2
N = [ sp.Lambda(x,(1-2*x)*(1-x)), sp.Lambda(x,4*x*(1-x)), sp.Lambda(x,x*(2*x-1))]

Ce sont les seules modifications à apporter par rapport aux programmes précédents, puisque le calcul des matrices élémentaires, des seconds membres élémentaires , l’assemblage, l’application des conditions aux limites et la résolution sont identiques (car écrit de façon générique).

On obtient ainsi la matrice élémentaire de rigidité dans le cas de coefficient constant:

\[\begin{split} K_e^k = \left[\begin{matrix}\frac{7 K}{3 h} & - \frac{8 K}{3 h} & \frac{K}{3 h}\\- \frac{8 K}{3 h} & \frac{16 K}{3 h} & - \frac{8 K}{3 h}\\\frac{K}{3 h} & - \frac{8 K}{3 h} & \frac{7 K}{3 h}\end{matrix}\right] \end{split}\]

qui est bien symétrique, avec une somme des lignes et des colonnes égales à zéro.

De même on obtient la matrice élémentaire de masse dans le cas de coefficient constant:

\[\begin{split} M_e^k = \left[\begin{matrix}\frac{2 \alpha h}{15} & \frac{\alpha h}{15} & - \frac{\alpha h}{30}\\\frac{\alpha h}{15} & \frac{8 \alpha h}{15} & \frac{\alpha h}{15}\\- \frac{\alpha h}{30} & \frac{\alpha h}{15} & \frac{2 \alpha h}{15}\end{matrix}\right] \end{split}\]

qui est bien symétrique définie positive.

Enfin le second membre élémentaire s’écrit: $\( B_e^k = \left[\begin{matrix}h \left(\frac{2 F_{k}}{15} + \frac{F_{k+1}}{15} - \frac{F_{k+2}}{30}\right) \\ h \left(\frac{F_{k}}{15} + \frac{8 F_{k+1}}{15} + \frac{F_{k+2}}{15}\right) \\ h \left(- \frac{F_{k}}{30} + \frac{F_{k+1}}{15} + \frac{2 F_{k+2}}{15}\right)\end{matrix}\right] \)$

En utilisant ces programmes sur un maillage de \(N_{e}=4\) éléments (soit \(Nn=9\) inconnues), on obtiens la matrice \(\mathbf{A}\) suivante:

\[\begin{split}\mathbf{A}=\left[\begin{array}{ccccccccc} 1.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0\\ -669.0 & 1350.0 & -669.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0\\ 83.0 & -669.0 & 1180.0 & -669.0 & 83.0 & 0.0 & 0.0 & 0.0 & 0.0\\ 0.0 & 0.0 & -669.0 & 1350.0 & -669.0 & 0.0 & 0.0 & 0.0 & 0.0\\ 0.0 & 0.0 & 83.0 & -669.0 & 1180.0 & -669.0 & 83.0 & 0.0 & 0.0\\ 0.0 & 0.0 & 0.0 & 0.0 & -669.0 & 1350.0 & -669.0 & 0.0 & 0.0\\ 0.0 & 0.0 & 0.0 & 0.0 & 83.0 & -669.0 & 1180.0 & -669.0 & 83.0\\ 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & -669.0 & 1350.0 & -669.0\\ 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 83.0 & -669.0 & 590.0 \end{array}\right]\end{split}\]

et un second membre \(\mathbf{B}\) :

\[\mathbf{B}=[60.0,314.0,157.0,314.0,157.0,314.0,157.0,314.0,46.5]\]

La solution obtenue vaut:

\[\mathbf{X}=[60.0,55.3,51.4,48.2,45.7,43.8,42.4,41.6,41.3]\]

Les valeurs nodales de la solution sont très proche de la solution exacte, ce que confirme le calcule de l’erreur moyenne qui est encore plus faible qu’avec l’approximation \(P^{1}\) ( \(0.0054\) au lieu de \(0.083\)). Mais la grande différence avec l’approximation \(P^{1}\) se trouve sur le calcul du flux en \(x=L\) : on trouve un flux égale à \(30.16\) (au lieu de \(158\) en \(P^{1}\)), très proche de la valeur exacte \(32\). Dans ce cas l’approximation \(P^{2}\) apporte une meilleure précision sur la dérivée en \(x=L\), que l’approximation \(P^{1}\).

4.3.3. Etude de la précision

Pour quantifier cette étude, nous avons tracé l’erreur relative moyenne \(\frac{||u-u^{h}||}{||u||}\) et l’erreur relative sur la condition aux limites en \(x=L\) en fonction du nombre d’éléments \(Ne\) du maillage. Les résultats sont tracés en échelle logarithmique sur la figure suivante que l’on comparera avec la figure en \(\mathcal{P}^1\). On constate que l’erreur relative moyenne varie en \(\frac{1}{Ne^{3}}\) (comparaison avec une droite de pente \(-3\)), et que l’erreur relative sur la condition aux limites varie en \(\frac{1}{Ne^{3}}\). Ce dernier résultat est en sans doute lié au problème particulier traité, puisqu’en générale on attend une précision en \(\frac{1}{Ne^{2}}\) pour la dérivée avec une approximation \(P^{2}\). La précision de l’approximation \(P^{2}\) est donc d’ordre 3, i.e. en \(\theta(h^{3})\), alors que la précision de l’approximation \(P^{1}\) est d’ordre 2, i.e. en \(\theta(h^{2})\) (on a noté \(h\) la taille caractéristique des éléments \(h=\frac{L}{Ne}\))

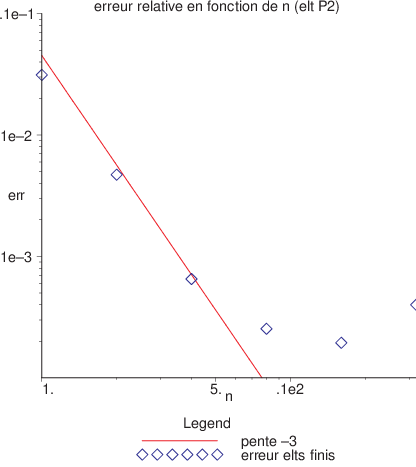
Fig. 4.20 Erreur relative en fonction de Ne(elt P2)

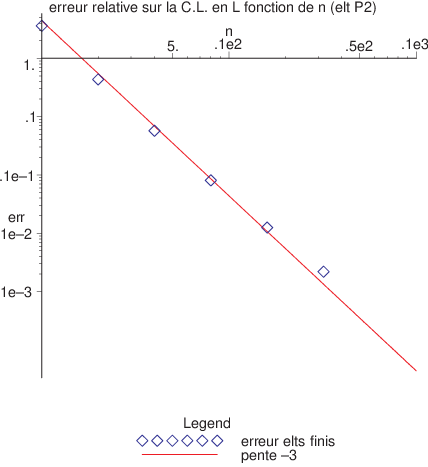
Fig. 4.21 Erreur relative sur la dérivée en fonction de Ne (elt P2)

Exercice: modifier le programme précédent pour faire l’étude avec des éléments \(P^{3}\). Montrez que dans ce cas la précision de l’approximation est d’ordre 4, i.e. en \(\theta(h^{4})\).

4.4. Applications au cas de coefficients non constants

Pour terminer cette étude, nous allons appliquer la méthode des éléments finis pour résoudre le problème précédent dans le cas où la section du barreau est variable: i.e. \(S=S(x)\), et l’extrémité \(x=L\) est à l’air libre. Ce problème est un problème classique d’ailette de radiateur, qui permet d’évacuer la chaleur d’un support à une température \(T_{e}\) par échange convectif avec l’air ambiant à température \(T_{a}\).

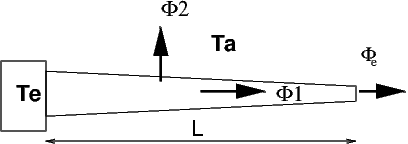
Fig. 4.22 Température dans un barreau de section variable

Dans ce cas le flux de chaleur \(\Phi_{e}\) à l’extrémité s’écrit: \(\Phi_{e}=hS(T-T_{a})\), et l’équation d’équilibre s’écrit:

\[\begin{split}\left\{ \begin{array}{c} -\frac{d}{dx}(K(x)\frac{dT}{dx})+\alpha(x)T=\alpha T_{a}\\ T(0)=T_{e},\,-K(L)\frac{dT}{dx}(L)=\alpha(L)\,(T(L)-T_{a}) \end{array}\right.\end{split}\]

Nous allons traiter avec les programmes précédents 3 cas correspondants à 3 ailettes de section rectangulaire variable. Ces 3 ailettes ont une longueur \(L=0.1\,m\), une largeur \(H=0.2\,m\), mais une épaisseur variable avec:

1. une section \(S(x)=H\,d(x)\) croissante d’épaisseur \(d(x)=0.025+0.050\frac{x}{L}\)

2. une section \(S(x)=H\,d(x)\) décroissante d’épaisseur \(d(x)=0.075-0.050\frac{x}{L}\)

3. une section \(S(x)=H\,d(x)\) constante d’épaisseur \(d(x)=0.05\,m\)

L’épaisseur moyenne étant la même pour les 3 ailettes, elles ont un même volume \(V=10^{-3}\,m^{3}\), mais des surfaces d’échange différentes.

Le programme ci-dessous donne les paramètres du problème dans le cas d’une convection forcée avec \(h=10^{4}\,W/m^{2}/K\).

En utilisant un maillage de \(Ne=16\) éléments \(P^{1}\), on obtiens les résultats suivants pour les 3 types d’ailette que l’on a tracé sur la figure suivante. A titre de comparaison, on a aussi tracé la solution analytique pour le cas 3 (ailette de section constante). Cela nous permet de vérifier que la solution éléments finis \(P^{1}\) avec un maillage de \(Ne=16\) éléments est suffisamment précise, puisque la solution exacte et la solution approchée sont quasiment confondues.

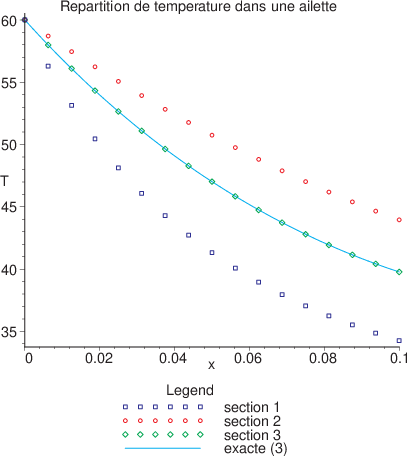
Fig. 4.23 Solution \(P^{1}\) pour les 3 sections d’ailette

On constate sur cette figure que la température à l’extrémité de l’ailette est la plus faible dans le cas 1, et la plus grande dans le cas 2. Cela peut s’expliquer par une surface d’échange plus grande à l’extrémité de l’ailette dans le cas 1 que dans le cas 2 ( 3 fois plus petite), et dans le cas 3 (2 fois plus petite).

Cependant si l’on calcul le flux de chaleur \(\phi=-kS(\frac{dT}{dx})_{x=0}\) évacué par l’ailette, on trouve les résultats suivants:

\[\phi_{1}=178650\,W,\,\,\phi_{2}=18620\,W,\,\,\phi_{3}=19350\,W\]

ce qui montre que dans ce cas l’ailette la plus efficace est l’ailette 3 de section constante. En effet même si dans le cas 1 la température dans l’ailette est plus faible, et donc le gradient de température plus important, la section en \(x=0\) est plus faible que dans le cas 3, et donc globalement le flux est plus petit. C’est exactement le contraire pour l’ailette 2.