6. Éléments finis en 2D

6.1. Une première approche

On considère l’écoulement incompressible à potentiel dans un canal bidimensionnel obturé partiellement par un obstacle carré. Les dimensions du problème sont indiquées sur la figure Fig. 6.1:

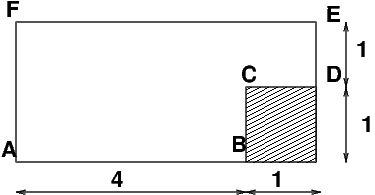
Fig. 6.1 écoulement potentiel dans un canal

L’équation d’équilibre régissant la fonction de courant \(\psi(x,y)\) n’est autre que l’équation de Laplace

\[\Delta\psi=\frac{\partial^{2}\psi}{\partial x^{2}}+\frac{\partial^{2}\psi}{\partial y^{2}}=0\]

où \(\psi(x,y)\) est la fonction de courant telle que:

\[u=\frac{\partial\psi}{\partial y},\,\,v=-\frac{\partial\psi}{\partial x}\]

\(u\) et \(v\) étant les composantes de la vitesse. Les conditions aux limites en vitesse pour ce problème sont:

1. en entrée, une vitesse constante suivant x : \(u=U_{0},\,v=0\)

2. en sortie, la même vitesse qu’en entrée : \(u=U_{0},\,v=0\)

3. une condition de glissement sur les parois: \(\overrightarrow{u}.\overrightarrow{n}=0\)

En utilisant la définition de \(\psi\), on en déduit les conditions aux limites pour la fonction de courant (en choisissant une origine pour \(\psi\) en \(y=0\)):

1. en entrée en \(x=-5H\) : \(\psi(-5H,y)=\int_{0}^{y}u\,dy=U_{0}y\)

2. en sortie en \(x=5H\) : \(\psi(5H,y)=\int_{0}^{y}u\,dy=U_{0}y\)

3. sur les parois : \(\psi=cste\)

Par raison de symétrie du domaine, des conditions aux limites et de l’équation du problème, on peut limiter le domaine d’étude au domaine \(\Omega\) de frontière ABCDEF (soit \(1/4\) du domaine initial). Les conditions aux limites sur ce domaine sont:

1. en entrée AF \((x=-5H)\) : \(\psi_{AF}=U_{0}y\),

2. sur l’axe AB \((y=0)\), on a une condition de symétrie \((v=0)\), et l’axe AB est la ligne de courant qui arrive sur l’obstacle. La valeur de \(\psi\) vaut donc \(\psi(-5H,0)\), soit \(\psi_{AB}=0,\)

3. sur l’obstacle BCD, la valeur de \(\psi\) est constante et égale à celle sur AB, soit \(\psi_{BCD}=0\),

4. sur la paroi supérieure EF \((y=2H)\), la valeur de \(\psi\) est constante et égale à \(\psi(-5H,2H)\), soit \(\psi_{EF}=2U_{0}H\)

5. sur la sortie DE, on impose une condition de symétrie \((\frac{\partial\psi}{\partial n})_{DE}=(\frac{\partial\psi}{\partial x})_{x=0}=0.\)

6.1.1. Formulation faible

La formulation faible du problème s’obtient en multipliant l’équation par une fonction test \(v(x,y)\), et en intégrant sur le domaine \(\Omega\) . En utilisant la formule de Green, on intègre par partie le terme en Laplacien pour tenir compte des conditions aux limites et symétriser le problème. En utilisant les conditions aux limites, et en interprétant la fonction test \(v(x,y)\) comme une variation \(\delta\psi\) de la solution \(\psi(x,y)\), la formulation faible s’écrit:

(6.1)\[\begin{split}\left\{ \begin{array}{cc} \mbox{Trouver }\,\psi(x,y)\mbox{ tq } & \psi_{AF}=U_{0}y,\,\psi_{ABCD}=0,\:\psi_{EF}=2U_{0}H\\ \int_{\Omega}\overrightarrow{grad}\psi.\overrightarrow{grad}v\,d\omega=0 & \forall\,v(x,y)\,\mbox{\, t.q.}\,v_{ABCD}=0,\,v_{EF}=0 \end{array}\right.\end{split}\]

Dans la suite, pour effectuer les calculs, nous choisirons comme valeurs numériques \(H=1\) et \(U_{0}=\frac{1}{2}\), ce qui impose un débit unité en entrée.

La formulation faible (6.1) est équivalente à la formulation variationnelle suivante:

(6.2)\[\begin{split}\left\{ \begin{array}{cc} \mbox{Trouver }\,\psi(x,y) & \mbox{ minimisant }\,J(\psi)\\ J(\psi)=\frac{1}{2}\int_{\Omega}(\overrightarrow{grad}\psi)^{2}\,d\omega & \mbox{ avec }\psi_{AF}=U_{0}y,\,\psi_{ABCD}=0,\:\psi_{EF}=2U_{0}H \end{array}\right.\end{split}\]

L’écoulement étudié est un écoulement potentiel, donc le champ de vitesse est le gradient d’un potentiel \(\phi(x,y)\):

\[u=\frac{\partial\phi}{\partial x},\,v=\frac{\partial\phi}{\partial y}\]

L’équation de continuité \(div\,\overrightarrow{u}=0\) impose à ce potentiel de vérifier l’équation de Laplace:

\[\Delta\phi=0\]

Le potentiel \(\phi\) et la fonction de courant \(\psi\) vérifient donc la même équation, mais avec des conditions aux limites différentes.

Exercice: montrez que ce sont deux familles de fonctions orthogonales, i.e. les courbes de potentiel \(\phi=cste\) sont perpendiculaires aux lignes de courant.

Les conditions aux limites sur le potentiel \(\phi\) sont:

1. en entrée AF \((x=-5H)\): \(\phi=5HU_{0}\)

2. en sortie DE \((x=0)\) : \(\phi=0\)

3. sur les parois ABCD et EF: \(\frac{\partial\phi}{\partial n}=0\)

La formulation variationnelle associée au potentiel est identique à celle sur la fonction de courant (aux conditions aux limites près):

(6.3)\[\begin{split}\left\{\begin{array}{cc} \mbox{Trouver }\,\phi(x,y) & \mbox{ minimisant }\,J(\phi)\\ J(\phi)=\frac{1}{2}\int_{\Omega}(\overrightarrow{grad}\phi)^{2}\,d\omega=0 & \mbox{ avec }\phi_{AF}=5HU_{0},\:\phi_{DE}=0 \end{array}\right.\end{split}\]

La fonctionnelle \(J(\phi)\) a une interprétation physique: c’est l’énergie cinétique totale:

\[J(\phi)=\frac{1}{2}\int_{\Omega}(u^{2}+v^{2})\,d\omega\]

La solution potentiel du problème (6.3) correspond donc au champ de vitesse qui minimise l’énergie cinétique globale parmi tous les champs de vitesse à potentiel vérifiant les conditions aux limites. Cette propriété, caractéristique des écoulements incompressibles à potentiel (ou irrotationnels), a été découverte par Lord Kelvin en 1849 [1].

Exercice: démontrer cette propriété.

6.1.2. Interpolation par éléments finis \(\mathcal{P}^{1}\)

Pour résoudre numériquement le problème (6.1), on cherche une solution approchée \(\psi^{h}(x,y)\). En éléments finis cette solution est définie par la donnée:

1. d’un maillage \(\mathcal{M}^{h}\) du domaine de calcul \(\Omega\),

2. d’une interpolation sur chaque élément du maillage.

Pour des éléments finis \(\mathcal{P}^{1}\), le maillage est un maillage triangulaire et l’interpolation est une interpolation polynomial de degré 1 sur chaque élément, et continue globalement. Pour le problème considéré, nous choisissons le maillage de la figure Fig. 6.2 qui contient \(ne=12\) éléments et \(nn=11\) sommets.

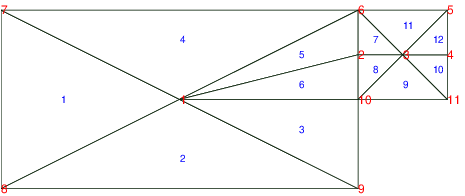
Fig. 6.2 maillage du canal de 11 noeuds et 12 éléments

La description d’un maillage comprend deux informations principales:

1. une information géométrique: les coordonnées de chacun des noeuds du maillage,

2. une information topologique: le numéro des 3 sommets de chacun des éléments du maillage, appelé table de connexion.

Ces informations sont données par 2 tableaux: un tableau \(\mathbf{X}\) de nombres réels de dimension \(2nn\) pour les coordonnées, et un tableau \(\mathbf{Tbc}\) de nombres entiers de dimension \(3ne\) pour la table de connexion. Pour le maillage de la figure précédente, les valeurs des deux tableaux sont données ci dessous.

Tableau 6.1 Coordonnées des noeuds du maillage

X	1	2
[1]	-3.0	1.0
[2]	-1.0	1.5
[3]	-0.5	1.5
[4]	0.0	1.5
[5]	0.0	2.0
[6]	-1.0	2.0
[7]	-5.0	2.0
[8]	-5.0	0.0
[9]	-1.0	0.0
[10]	-1.0	1.0
[11]	0.0	1.0

Tableau 6.2 Table de connexion du maillage

Tbc	1	2	3
[1]	1	7	8
[2]	8	9	1
[3]	9	10	1
[4]	1	6	7
[5]	2	6	1
[6]	1	10	2
[7]	6	2	3
[8]	2	10	3
[9]	10	11	3
[10]	11	4	3
[11]	3	5	6
[12]	3	4	5

Le domaine de calcul \(\Omega\) est donc discrétisé en \(ne\) éléments triangulaires \(e_{k}\) :

\[\Omega=\mathcal{M}^{h}=\bigcup_{k=1}^{ne}e_{k}\,\,\,\mbox{ avec }e_{k}\,\mbox{ triangle }\,\mbox{ de sommets }\{Tbc(k,1),Tbc(k,2),Tbc(k,3)\}\]

6.1.2.1. Interpolation sur un élément finis \(\mathcal{P}^{1}\)

Sur chaque élément \(e_{k}\) du maillage, l’approximation \(f^{h}\) par élément finis \(\mathcal{P}^{1}\) d’une fonction \(f(x,y)\) est un polynôme de degré 1 en \(x\) et \(y\), qui s’écrit:

\[f_{|e_{k}}^{h}=ax+by+c\]

Pour déterminer ce polynôme, il faut 3 points d’interpolation \(\{P_{j}\}_{j=1,3}\) et la valeur de la fonction \(\{F_{j}=f(P_{j})\}_{j=1,3}\) en ces 3 points. Les 3 équations \(\{P(x_{j},y_{j})=F_{j}\}_{j=1,3}\) permettent alors de déterminer les 3 coefficients de \(f_{|e_{k}}^{h}\). Pour assurer la condition de continuité globale de la solution, on choisit comme points d’interpolation les 3 sommets \(\{S_{j}^{k}\}_{j=1,3}\) du triangle \(k\) . L’approximation est donc définie par ses valeurs aux \(nn\) noeuds du maillage.

Considérons par exemple la fonction \(f(x,y)=(1+\frac{x}{10})(\frac{y}{2})^{4}\) sur le maillage. Elle est définie par le tableau de valeurs nodales \(F\) suivants:

\[F=[0.0437,\,0.2848,\,0.306,\,0.3164,\,1.0,\,0.9,\,0.5,\,0.0,\,0.0,\,0.0563,\,0.0625]\]

et elle est tracée en 3D et en iso-valeurs sur la figure Fig. 6.3 et Fig. 6.4:

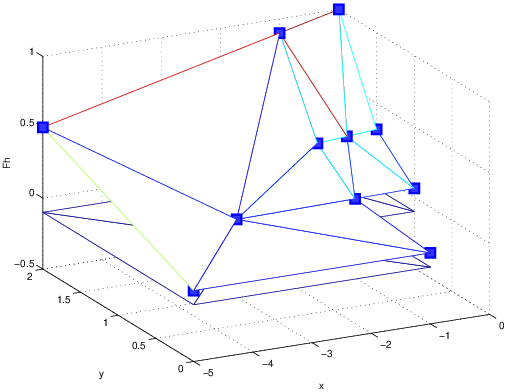
Fig. 6.3 Interpolation \(\mathcal{P}^{1}\) en 2D

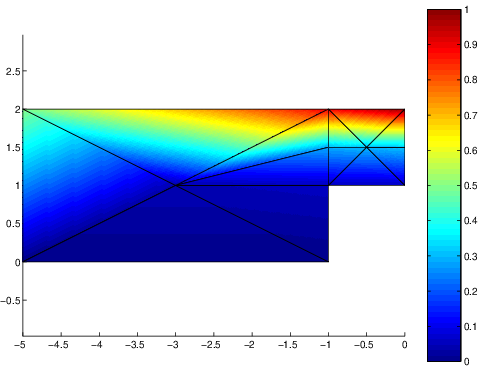
Fig. 6.4 Interpolation \(\mathcal{P}^{1}\) en 2D

Sur l’élément 5 qui a pour sommets les noeuds \(\{n_{1}=2,n_{2}=6,n_{3}=1\}\), cette fonction est le polynôme de degré 1 qui prend les valeurs \(F_{n_{1}}=0.2848,\,F_{n_{2}}=0.9,\,F_{n_{3}}=0.047\) sur ces 3 sommets. Dans l’espace c’est un plan qui est représenté en perspective sur la figure précédente. Son expression analytique \(f_{|e_{5}}^{h}=ax+by+c\) est obtenue en résolvant le système de 3 équations à 3 inconnues \(\{a,b,c\}\):

(6.4)\[\begin{split}\left\{ \begin{array}{ccc} ax_{n_{1}}+by_{n_{1}}+c & = & F_{n_{1}}\\ ax_{n_{2}}+by_{n_{2}}+c & = & F_{n_{2}}\\ ax_{n_{3}}+by_{n_{3}}+c & = & F_{n_{3}} \end{array}\right.\end{split}\]

où \(\{x_{n_{1}},y_{n_{1}}\}\) sont les coordonnées du premier sommet \(S_{1}\) (de numéro \(n_{1}=2\)), \(\{x_{n_{2}},y_{n_{2}}\}\) les coordonnées du second sommet \(S_{2}\) (de numéro \(n_{2}=6\)), \(\{x_{n_{3}},y_{n_{3}}\}\) les coordonnées du troisième sommet \(S_{3}\) (de numéro \(n_{3}=1\)).

La résolution du système (6.4) permet d’obtenir les expressions suivantes pour \(\{a,b,c\}\)

(6.5)\[\begin{split}\left\{ \begin{array}{c} a=\frac{(y_{n_{2}}-y_{n_{3}})F_{n_{1}}+(y_{n_{3}}-y_{n_{1}})F_{n_{2}}+(y_{n_{1}}-y_{n_{2}})F_{n_{3}}}{(x_{n_{2}}-x_{n_{1}})(y_{n_{3}}-y_{n_{1}})-(x_{n_{3}}-x_{n_{1}})(y_{n_{2}}-y_{n_{1}})}\\ b=-\frac{(x_{n_{2}}-x_{n_{3}})F_{n_{1}}+(x_{n_{3}}-x_{n_{1}})F_{n_{2}}+(x_{n_{1}}-x_{n_{2}})F_{n_{3}}}{(x_{n_{2}}-x_{n_{1}})(y_{n_{3}}-y_{n_{1}})-(x_{n_{3}}-x_{n_{1}})(y_{n_{2}}-y_{n_{1}})}\\ c=\frac{(x_{n_{2}}y_{n_{3}}-x_{n_{3}}y_{n_{2}})F_{n_{1}}+(x_{n_{3}}y_{n_{1}}-x_{n_{1}}y_{n_{3}})F_{n_{2}}+(x_{n_{1}}y_{n_{2}}-x_{n_{2}}y_{n_{1}})F_{1}}{(x_{n_{2}}-x_{n_{1}})(y_{n_{3}}-y_{n_{1}})-(x_{n_{3}}-x_{n_{1}})(y_{n_{2}}-y_{n_{1}})} \end{array}\right.\end{split}\]

Les relations (6.5) montrent que l’interpolation \(\mathcal{P}^{1}\) de \(f(x,y)\) sur l’élément \(e_{k}\) ( \(f_{|e_{k}}^{h}\)) est une combinaison linéaire des valeurs nodales \(\{F_{n_{1}},F_{n_{2}},F_{n_{3}}\}\), qui s’écrit:

(6.6)\[f_{|e_{k}}^{h}(x,y)=F_{n_{1}}\,p_{1}(x,y)+F_{n_{2}}\,p_{2}(x,y)+F_{n_{3}}\,p_{3}(x,y)\]

Les fonctions \(\{p_{1}(x,y),\,p_{2}(x,y),\,p_{3}(x,y)\}\) sont les 3 polynômes de degré 1, associés aux 3 sommets \(\{S_{1},S_{2},S_{3}\}\) de l’élément, suivants:

(6.7)\[\begin{split}\left\{ \begin{array}{c} p_{1}(x,y)=\frac{(y_{n_{2}}-y_{n_{3}})\,x+(x_{n_{3}}-x_{n_{2}})\,y+(x_{n_{2}}y_{n_{3}}-x_{n_{3}}y_{n_{2}})}{(x_{n_{2}}-x_{n_{1}})(y_{n_{3}}-y_{n_{1}})-(x_{n_{3}}-x_{n_{1}})(y_{n_{2}}-y_{n_{1}})}\\ p_{2}(x,y)=\frac{(y_{n_{3}}-y_{n_{1}})\,x+(x_{n_{1}}-x_{n_{3}})\,y+(x_{n_{3}}y_{n_{1}}-x_{n_{1}}y_{n_{3}})}{(x_{n_{2}}-x_{n_{1}})(y_{n_{3}}-y_{n_{1}})-(x_{n_{3}}-x_{n_{1}})(y_{n_{2}}-y_{n_{1}})}\\ p_{3}(x,y)=\frac{(y_{n_{1}}-y_{n_{2}})\,x+(x_{n_{2}}-x_{n_{1}})\,y+(x_{n_{1}}y_{n_{2}}-x_{n_{2}}y_{n_{1}})}{(x_{n_{2}}-x_{n_{1}})(y_{n_{3}}-y_{n_{1}})-(x_{n_{3}}-x_{n_{1}})(y_{n_{2}}-y_{n_{1}})} \end{array}\right.\end{split}\]

Ces polynômes de degré 1 (dont on vérifie les symétries par permutation d’indices) vérifient :

\[p_{i}(S_{j})=\delta_{ij}\,\mbox{ pour }\,i,j=1,3\]

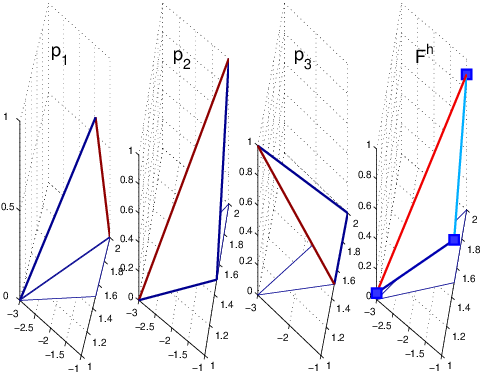
Fig. 6.5 polynômes \(p_{1},p_{2},p_{3}\) et interpolation \(f^{h}\) sur l’élément 5 (2,6,1)

Ainsi le polynôme \(p_{1}(x,y)\) vaut 1 sur le sommet \(S_{1}\) et 0 sur les 2 autres sommets \(S_{2}\) et \(S_{3}\); de même pour \(p_{2}(x,y)\) et \(p_{3}(x,y)\) avec une permutation des indices. La représentation en perspective de ces 3 fonctions est donnée sur la figure ci-dessus (pour le tracé on a remplacer les coordonnées des sommets par leurs valeurs obtenues dans le tableau de la table de connexion: i.e.

\[\begin{split}\begin{aligned} x_{n_{1}}=X(2,1)=-1.0,\,\,\,\,\,y_{n_{1}}=X(2,2)=1.5,\\ x_{n_{2}}=X(6,1)=-1.0,\,\,\,\,\,y_{n_{2}}=X(6,2)=2.0,\\ x_{n_{3}}=X(1,1)=-3.0,\,\,\,\,\,y_{n_{3}}=X(1,2)=1.0,\end{aligned}\end{split}\]

Ces polynômes vérifient en outre la relation:

\[p_{1}(x,y)+p_{2}(x,y)+p_{3}(x,y)=1\]

Dans le cas d’une interpolation \(\mathcal{P}^{1}\), ces polynômes ont une interprétation géométrique. Ce sont les coordonnées barycentriques. Ces coordonnées sont définies de la façon suivante: pour chaque point \(M\) de coordonnées \((x,y)\), le vecteur \(\overrightarrow{OM}\) s’écrit en fonction des sommets du triangle, comme combinaison des vecteurs \(\overrightarrow{OS_{1}}\), \(\overrightarrow{OS_{2}}\), \(\overrightarrow{OS_{3}}\). Les coefficients sont les coordonnées barycentriques par rapport au triangle considéré, i.e.

(6.8)\[\overrightarrow{OM}=\lambda_{1}\overrightarrow{OS_{1}}+\lambda_{2}\overrightarrow{OS_{2}}+\lambda_{3}\overrightarrow{OS_{3}}\,\,\forall O\,\,\,\mbox{ avec }\,\lambda_{1}+\lambda_{2}+\lambda_{3}=1\]

Les valeurs de \(\lambda_{1},\lambda_{2},\lambda_{3}\) vérifient les relations (voir la figure pour les notations):

\[\begin{split}\begin{aligned} \lambda_{1}=\frac{Aire(MS_{2}S_{3})}{Aire(S_{1}S_{2}S_{3})}=\frac{\frac{1}{2}\overline{MH_{1}}\overline{.S_{2}S_{3}}}{Aire(S_{1}S_{2}S_{3})}\nonumber \\ \lambda_{2}=\frac{Aire(MS_{3}S_{1})}{Aire(S_{1}S_{2}S_{3})}=\frac{\frac{1}{2}\overline{MH_{2}}\overline{.S_{3}S_{1}}}{Aire(S_{1}S_{2}S_{3})}\label{c4eq4b}\\ \lambda_{3}=\frac{Aire(MS_{1}S_{2})}{Aire(S_{1}S_{2}S_{3})}=\frac{\frac{1}{2}\overline{MH_{3}}\overline{.S_{1}S_{2}}}{Aire(S_{1}S_{2}S_{3})}\nonumber \end{aligned}\end{split}\]

qui sont justement les expressions (6.7) des polynômes \(\{p_{1},p_{2},p_{3}\}\).

Exercice: démontrer ces relations

On a aussi une propriété remarquable des coordonnées barycentriques: un point \(M\) est à l’intérieur du triangle si et seulement si ses 3 coordonnées barycentriques sont positives, il est sur un des cotés du triangle si la coordonnée barycentrique par rapport au coté opposé est nulle, et il est à l’extérieur du triangle si une au moins des coordonnées barycentriques est négative.

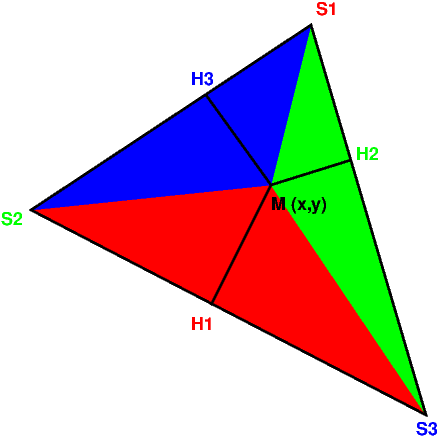
Fig. 6.6 coordonnées barycentriques

6.1.3. Approximation par éléments finis \(\mathcal{P}^{1}\)

L’approximation par éléments finis est donc définie de façon locale sur chaque élément, en calculant des formules d’interpolation du type (6.6) et (6.7). De façon a obtenir une expression générique pour l’interpolation, on va, comme dans le chapitre précédent introduire une transformation d’un élément \(e_{k}\) vers un élément de référence. Cet élément de référence est le triangle rectangle unité dans le plan de référence \((\xi,\eta)\) (voir figure Fig. 6.7).

6.1.3.1. Interpolation sur l’élément de référence

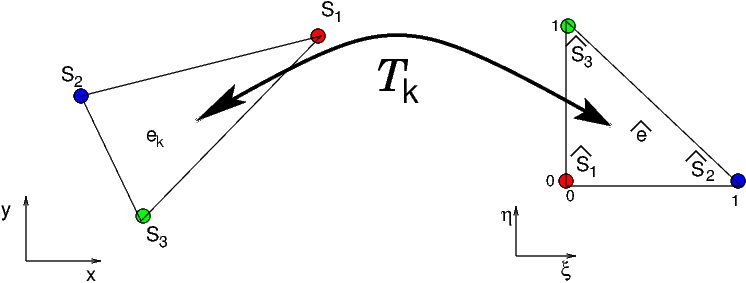
Fig. 6.7 transformation \(\mathcal{T}_{k}:\,(x,y)\Leftrightarrow(\xi,\eta)\) vers l’élément de référence \(\mathcal{P}^{1}\)

Cette transformation \(\mathcal{T}^{k}\) est une transformation affine:

(6.9)\[\begin{split}\mathcal{T}_{k}\,\left\{ \begin{array}{ccc} e^{k} & \Longleftrightarrow & \hat{e}\\ \left[\begin{array}{c} x\\ y \end{array}\right] & \Longleftrightarrow & \left[\begin{array}{c} \xi\\ \eta \end{array}\right] \end{array}\right.\end{split}\]

dont l’expression de \((\xi\,\eta)\) en fonction de \((x,y)\) s’écrit :

\[\begin{split}\left[\begin{array}{c} \xi\\ \eta \end{array}\right]=\left[\begin{array}{cc} a_{11} & a_{12}\\ a_{21} & a_{22} \end{array}\right]\left[\begin{array}{c} x\\ y \end{array}\right]+\left[\begin{array}{c} b_{1}\\ b_{2} \end{array}\right]\end{split}\]

Les 6 coefficients de la transformation sont déterminés par les conditions de transformation des 3 sommets \(\{S_{i}\}_{i=1,3}\) de \(e_{k}\) vers les 3 sommets \(\{\hat{S}_{i}\}_{i=1,3}\) de l’élément de référence \(\hat{e}\):

\[\left\{ \hat{S}_{i}=T_{k}(S_{i})\right\} _{i=1,3}\]

On remarque que \(\xi(x,y)\) est un polynôme de degré 1 en \((x,y)\), qui vaut 0 en \(S_{1}\) (car \(\xi(\hat{S}_{1})=0\)) , 1 en \(S_{2}\) (car \(\xi(\hat{S}_{2})=1\)), et 0 en \(S_{3}\) (car \(\xi(\hat{S}_{3})=0\)). C’est donc le polynôme d’interpolation \(p_{2}(x,y)\) (ou la coordonnée barycentrique \(\lambda_{2}(x,y)\)) associé au sommet \(S_{2}\), dont l’expression est donnée en (6.7). De même \(\eta(x,y)\) est un polynôme de degré 1 en \((x,y)\), qui vaut 0 en \(S_{1}\) (car \(\eta(\hat{S}_{1})=0\)), 0 en \(S_{2}\) (car \(\eta(\hat{S}_{2})=0\)), et 1 en \(S_{3}\) (car \(\eta(\hat{S}_{3})=1\)). C’est donc le polynôme d’interpolation de Lagrange\(p_{3}(x,y)\) (ou la coordonnée barycentrique \(\lambda_{3}(x,y)\)) associé au sommet \(S_{3}\). On a donc:

\[\xi=\lambda_{2}(x,y),\,\,\,\eta=\lambda_{3}(x,y)\]

et

\[1-\xi-\eta=\lambda_{1}(x,y)\]

En notant \((x_{n_{q}},y_{n_{q}})\) les coordonnées du sommet \(S_{q}\) de l’élément \(e_{k}\), on obtiens l’expression générique de la transformation de \(e_{k}\) vers l’élément de référence \(\hat{e}\):

(6.10)\[\begin{split}\begin{aligned} \xi=\frac{(y_{n_{3}}-y_{n_{1}})\,x+(x_{n_{1}}-x_{n_{3}})\,y+(x_{n_{3}}y_{n_{1}}-x_{n_{1}}y_{n_{3}})}{(x_{n_{2}}-x_{n_{1}})(y_{n_{3}}-y_{n_{1}})-(x_{n_{3}}-x_{n_{1}})(y_{n_{2}}-y_{n_{1}})}\\ \eta=\frac{(y_{n_{1}}-y_{n_{2}})\,x+(x_{n_{2}}-x_{n_{1}})\,y+(x_{n_{1}}y_{n_{2}}-x_{n_{2}}y_{n_{1}})}{(x_{n_{2}}-x_{n_{1}})(y_{n_{3}}-y_{n_{1}})-(x_{n_{3}}-x_{n_{1}})(y_{n_{2}}-y_{n_{1}})}\end{aligned}\end{split}\]

Sur cet élément de référence, les 3 polynômes d’interpolation \(\{p_{1},p_{2},p_{3}\}\) ont une expression très simple: ce sont les fonctions forme \(\{N_{1},N_{2},N_{3}\}\) de l’approximation \(\mathcal{P}^{1}\) sur l’élément de référence associées aux 3 sommets \(\{\hat{S}_{1},\hat{S}_{2},\hat{S}_{3}\}\):

(6.11)\[N_{1}(\xi,\eta)=1-\xi-\eta,\,\,N_{2}(\xi,\eta)=\xi,\,\,N_{3}(\xi,\eta)=\eta\]

Pour les calculs d’intégrale, on aura besoin du changement de variables \(x=x(\xi\,\eta)\) et \(y=y(\xi,\eta)\), qui correspond donc à la transformation réciproque. Cette transformation étant affine, \(x(\xi\,\eta)\) est une combinaison linéaire des valeurs aux noeuds, i.e. des abscisses \(\{x_{n_{q}}\}\) des sommets de l’élément \(e_{k}\), et de même pour \(y(\xi,\eta)\). On a donc

(6.12)\[\begin{split}\begin{aligned} x=x_{n_{1}}N_{1}(\xi,\eta)+x_{n_{2}}N_{2}(\xi,\eta)+x_{n_{3}}N_{3}(\xi,\eta)\\ y=y_{n_{1}}N_{1}(\xi,\eta)+y_{n_{2}}N_{2}(\xi,\eta)+y_{n_{3}}N_{3}(\xi,\eta) \end{aligned}\end{split}\]

Exercice: montrer qu’en écrivant ces relations (6.12) en variable (x,y) on retrouve la relation (6.10) sur les coordonnées barycentriques.

La matrice jacobienne \(\mathbf{J}_{k}\)= \(\frac{D(x,y)}{D(\xi,\eta)}\) de cette transformation se calcule simplement:

(6.13)\[\begin{split}\mathbf{J}_{k}=\left[\begin{array}{cc} \frac{\partial x}{\partial\xi} & \frac{\partial x}{\partial\eta}\\ \frac{\partial y}{\partial\xi} & \frac{\partial y}{\partial\eta} \end{array}\right]=\left[\begin{array}{cc} (x_{n_{2}}-x_{n_{1}}) & (x_{n_{3}}-x_{n_{1}})\\ (y_{n_{2}}-y_{n_{1}}) & (y_{n_{3}}-x_{n_{1}}) \end{array}\right]\end{split}\]

De même la matrice jacobienne de la transformation inverse \(\frac{D(\xi,\eta)}{D(x,y)}\) est égale à l’inverse de \(\mathbf{J}^{k}\):

(6.14)\[\begin{split}\mathbf{J}_{k}^{-1}=\left[\begin{array}{cc} \frac{\partial\xi}{\partial x} & \frac{\partial\xi}{\partial y}\\ \frac{\partial\eta}{\partial x} & \frac{\partial\eta}{\partial y} \end{array}\right]=\frac{1}{2\,aire_{k}}\left[\begin{array}{cc} (y_{n_{3}}-y_{n_{1}}) & (x_{n_{1}}-x_{n_{3}})\\ (y_{n_{1}}-y_{n_{2}}) & (x_{n_{2}}-x_{n_{1}}) \end{array}\right]\end{split}\]

en notant

\[aire_{k}=\frac{1}{2}((x_{n_{2}}-x_{n_{1}})(y_{n_{3}}-y_{n_{1}})-(x_{n_{3}}-x_{n_{1}})(y_{n_{2}}-y_{n_{1}}))\]

l’aire du triangle \(e^{k}\).

En notant \(\{n_{1},n_{2},n_{3}\}\) les numéros des 3 sommets de l’élément \(e_{k}\) qui sont donnés par la table de connexion ( \(n_{1}=Tbc(k,1)\), \(n_{2}=Tbc(k,2)\), \(n_{3}=Tbc(k,3)\)), l’approximation \(f^{h}\) s’écrit sur l’élément \(e_{k}\):

(6.15)\[f_{|e_{k}}^{h}(\xi,\eta)=F_{n_{1}}N_{1}(\xi,\eta)+F_{n_{2}}N_{2}(\xi,\eta)+F_{n_{3}}N_{3}(\xi,\eta)\]

Cette expression a la même forme que la relation (6.6), mais l’expression (6.11) des fonctions de forme est beaucoup plus simple que l’expression (6.7)des polynômes d’interpolation, ce qui va nous permettre en particulier un calcul plus simple des intégrales dans la formulation faible.

Attention: la dérivée d’une fonction dans l’élément de référence n’est évidemment pas égale à la dérivée dans le plan physique \((x,y)\). Il faut tenir compte du changement de variable:

\[\frac{\partial f}{\partial x}=\frac{\partial f}{\partial\xi}\frac{\partial\xi}{\partial x}+\frac{\partial f}{\partial\eta}\frac{\partial\eta}{\partial x}\]

qui s’écrit en fonction de la transposée de l’inverse de la matrice jacobienne \(\mathbf{J}^{k}\). Le vecteur gradient s’écrit:

\[\overrightarrow{\nabla_{x,y}}f=(\mathbf{J}_{k}^{-1})^{t}\overrightarrow{\nabla_{\xi,\eta}}f\]

(6.16)\[\begin{split}\left[\begin{array}{c} \frac{\partial f}{\partial x}\\ \frac{\partial f}{\partial y} \end{array}\right]=\left[\begin{array}{cc} \frac{\partial\xi}{\partial x} & \frac{\partial\eta}{\partial x}\\ \frac{\partial\xi}{\partial y} & \frac{\partial\eta}{\partial y} \end{array}\right]\left[\begin{array}{c} \frac{\partial f}{\partial\xi}\\ \frac{\partial f}{\partial\eta} \end{array}\right]\end{split}\]

6.1.3.2. Fonctions de base

Nous avons montré que l’approximation \(f^{h}(x,y)\) par éléments finis \(\mathcal{P}^{1}\) d’une fonction \(f(x,y)\) sur un maillage était déterminée par les valeurs nodales \(\{F_{i}\}\) de \(f\) aux \(nn=11\) noeuds \(\{M_{i}\}\) du maillage. Sur chaque élément, \(f^{h}\) est un polynôme de degré 1 donnée par l’expression (6.15), qui est une fonction linéaire des 3 valeurs aux sommets de l’élément.

On peut donc écrire l’approximation \(f^{h}(x,y)\) comme une combinaison linéaire des valeurs nodales \(\{F_{i}=f^{h}(M_{i})\}_{i=1,nn}\) :

\[f^{h}(x,y)=\sum_{i=1}^{nn}F_{i}\Phi_{i}(x,y)\]

Les fonctions \(\Phi_{i}(x,y)\) sont les fonctions de base de l’approximation. Elles sont telles que sur chaque élément \(e_{k}\) on retrouve l’approximation (6.15), ce sont donc des polynômes de degré 1 en \((x,y)\). De plus elles vérifient la propriété suivante pour chaque noeud \(M_{j}\) du maillage de coordonnées \((x_{j},y_{j})\):

\[\Phi_{i}(M_{j})=\Phi_{i}(x_{j},y_{j})=\delta_{ij}\]

Autrement dit la fonction de base \(\Phi_{i}(x,y)\) est une fonction continue qui vaut 1 au noeud \(i\) du maillage, 0 sur tout les autres noeuds, et qui sur chaque élément est un polynôme de degré 1. On en déduit que sur un élément \(e_{k}\) dont le noeud \(i\) n’est pas un sommet, la fonction \(\Phi_{i}(x,y)\) est identiquement nulle (car elle est nulle sur les trois sommets). Le support de la fonction \(\Phi_{i}(x,y)\) (i.e. le lieu des points où la fonction est non nulle) se limite donc aux éléments du maillage ayant le noeud \(i\) pour sommet:

(6.17)\[\begin{split}\Phi_{i}(x,y)=\left\{ \begin{array}{ccc} 0 & \mbox{sur l'élément}\,k\,\,t.q. & M_{i}\notin e_{k}\\ N_{q}(\xi,\eta) & \mbox{sur l'élément }\,k\,tq. & M_{i}=S_{q} \end{array}\right.\end{split}\]

Ainsi la fonction de base \(\Phi_{2}(x,y)\) est non nulle uniquement sur les éléments \(\{5,6,7,8\}\) et vaut

\[\begin{split}\Phi_{2}(x,y)=\left\{ \begin{array}{cc} N_{1}(\xi,\eta) & \mbox{sur}\,e_{5}\\ N_{3}(\xi,\eta) & \mbox{sur}\,e_{6}\\ N_{2}(\xi,\eta) & \mbox{sur}\,e_{7}\\ N_{1}(\xi,\eta) & \mbox{sur}\,e_{8}\\ 0 & \mbox{sinon} \end{array}\right.\end{split}\]

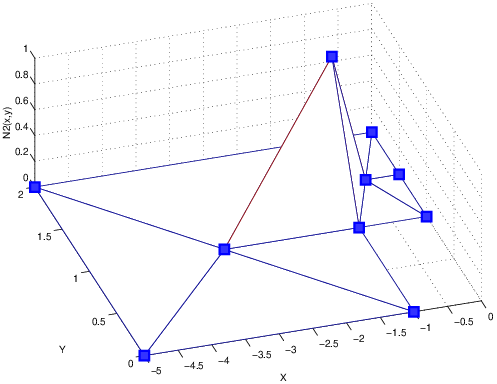
Fig. 6.8 fonction de base \(\Phi_{2}(x,y)\)

En effet le sommet 2 est le premier sommet sur l’élément \(e_{5}\) dans la table de connection ([1.2], (i.e. Tbc(5,1)=2); le troisième sur l’élément \(e_{6}\) (i.e. Tbc(6,3)=2), le second sur l’élément \(e_{7}\) (i.e. Tbc(7,2)=1), et enfin le premier sur l’élément \(e_{8}\) (i.e. Tbc(8,1)=2). Cette fonction de base \(\Phi_{2}(x,y)\) est tracée en perspective sur la figure ci-dessus, et sa forme est une forme pyramidale.

6.1.4. Formulation faible discrète

La solution approchée \(\psi^{h}\) du problème (6.1) est donc définie à partir de ces \(nn=11\) valeurs nodales \(\{\psi_{i}\}_{i=1,nn}\) aux sommets du maillage.

\[\psi^{h}(x,y)=\sum_{i=1}^{nn}\psi_{i}\Phi_{i}(x,y)\]

La solution du problème (6.1) doit de plus vérifiée les conditions aux limites fortes, i.e.:

\[\psi_{ABCD}^{h}=0,\:\psi_{EF}^{h}=2U_{0}H,\,\Psi_{AF}^{h}=U_{0}y\]

donc la valeur de \(\psi^{h}\) est fixé sur les noeuds du maillage se trouvant sur ces frontières:

\[\psi_{8}=\psi_{9}=\psi_{10}=\psi_{11}=0,\,\,\,\psi_{5}=\psi_{6}=\psi_{7}=\psi^{e}\,\mbox{ avec }\,\psi^{e}=2U_{0}H\]

Grâce à un choix judicieux de la numérotation des noeuds du maillage, la solution approchée \(\psi^{h}\) s’écrit:

(6.18)\[\psi^{h}(x,y)=\sum_{j=1}^{4}\psi_{j}\Phi_{j}(x,y)\,+\,\psi^{e}*(\Phi_{5}(x,y)+\Phi_{6}(x,y)+\Phi_{7}(x,y))\]

Après application des conditions aux limites de Dirichlet, le problème discrétisé possède 4 degrés de liberté. En remplaçant la solution exacte par la solution approchée (6.18) dans (6.1), il vient la formulation faible discrète:

(6.19)\[\begin{split}\begin{aligned} \int_{\Omega}\left\{ \frac{\partial}{\partial x}\left(\sum_{j=1}^{4}\psi_{j}\Phi_{j}(x,y)+\psi^{e}\sum_{j=5}^{7}\Phi_{j}(x,y)\right)\frac{\partial v^{h}}{\partial x}\right. & + \\ \left.\frac{\partial}{\partial y}\left(\sum_{j=1}^{4}\psi_{j}\Phi_{j}(x,y)+\psi^{e}\sum_{j=5}^{7}\Phi_{j}(x,y)\right)\frac{\partial v^{h}}{\partial y}\right\} dxdy & = & 0\end{aligned}\end{split}\]

Les fonctions tests \(v^{h}\)sont déduites de la forme de la solution approchée (6.18), puisque ce sont des variations \(\delta\psi^{h}\) de \(\psi^{h}\):

\[v^{h}(x,y)=\delta\psi^{h}=\sum_{i=1}^{4}\delta\psi_{i}\,\Phi_{i}(x,y)\]

On vérifie que ces fonctions s’annulent sur les frontières de Dirichlet. Ce sont des combinaisons linéaires des 4 fonctions de base \(\{\Phi_{i}\}_{i=1,4}\) associées aux 4 degrés de liberté \(\{\psi_{i}\}_{i=1,4}\).

En choisissant comme fonctions tests \(v^{h}\) dans (6.19), respectivement ces 4 fonctions de base \(\{\Phi_{i}\}_{i=1,4}\), on obtiens les 4 équations qui vont permettre de calculer les 4 inconnues \(\{\psi_{i}\}_{i=1,4}\):

\[\begin{split}\begin{aligned} \int_{\Omega}\left[\frac{\partial}{\partial x}\left(\sum_{j=1}^{4}\psi_{j}\Phi_{j}+\psi^{e}\sum_{j=5}^{7}\Phi_{j}\right)\frac{\partial\Phi_{i}}{\partial x}\right. & +\\ \left.\frac{\partial}{\partial y}\left(\sum_{j=1}^{4}\psi_{j}\Phi_{j}+\psi^{e}\sum_{j=5}^{7}\Phi_{j}\right)\frac{\partial\Phi_{i}}{\partial y}\right]dxdy & =0 & (i=1,4)\end{aligned}\end{split}\]

Après regroupement des termes, en permutant l’intégration et la sommation, les équations s’écrivent:

\[\sum_{j=1}^{4}\psi_{j}\int_{\Omega}\left(\frac{\partial\Phi_{j}}{\partial x}\frac{\partial\Phi_{i}}{\partial x}+\frac{\partial\Phi_{j}}{\partial y}\frac{\partial\Phi_{i}}{\partial y}\right)d\omega=-\sum_{j=5}^{7}\psi^{e}\int_{\Omega}\left(\frac{\partial\Phi_{j}}{\partial x}\frac{\partial\Phi_{i}}{\partial x}+\frac{\partial\Phi_{j}}{\partial y}\frac{\partial\Phi_{i}}{\partial y}\right)d\omega\]

C’est un système linéaire de 4 équations à 4 inconnues, qui s’écrit sous la forme matricielle: \(\mathbf{AX}=\mathbf{B}\) , où la matrice \(\mathbf{A}\) , le second membre \(\mathbf{B}\) et le vecteur inconnu \(\mathbf{X}\) sont donnés par:

\[\begin{split}\mathbf{A}=\left[\begin{array}{cccc} \int_{\Omega}\overrightarrow{\nabla}\Phi_{1}.\overrightarrow{\nabla}\Phi_{1}d\omega & \int_{\Omega}\overrightarrow{\nabla}\Phi_{2}.\overrightarrow{\nabla}\Phi_{1}d\omega & \int_{\Omega}\overrightarrow{\nabla}\Phi_{3}.\overrightarrow{\nabla}\Phi_{1}d\omega & \int_{\Omega}\overrightarrow{\nabla}\Phi_{4}.\overrightarrow{\nabla}\Phi_{1}d\omega\\ \int_{\Omega}\overrightarrow{\nabla}\Phi_{1}.\overrightarrow{\nabla}\Phi_{2}d\omega & \int_{\Omega}\overrightarrow{\nabla}\Phi_{2}.\overrightarrow{\nabla}\Phi_{2}d\omega & \int_{\Omega}\overrightarrow{\nabla}\Phi_{3}.\overrightarrow{\nabla}\Phi_{2}d\omega & \int_{\Omega}\overrightarrow{\nabla}\Phi_{4}.\overrightarrow{\nabla}\Phi_{2}d\omega\\ \int_{\Omega}\overrightarrow{\nabla}\Phi_{1}.\overrightarrow{\nabla}\Phi_{3}d\omega & \int_{\Omega}\overrightarrow{\nabla}\Phi_{2}.\overrightarrow{\nabla}\Phi_{3}d\omega & \int_{\Omega}\overrightarrow{\nabla}\Phi_{3}.\overrightarrow{\nabla}\Phi_{3}d\omega & \int_{\Omega}\overrightarrow{\nabla}\Phi_{4}.\overrightarrow{\nabla}\Phi_{3}d\omega\\ \int_{\Omega}\overrightarrow{\nabla}\Phi_{1}.\overrightarrow{\nabla}\Phi_{4}d\omega & \int_{\Omega}\overrightarrow{\nabla}\Phi_{2}.\overrightarrow{\nabla}\Phi_{4}d\omega & \int_{\Omega}\overrightarrow{\nabla}\Phi_{3}.\overrightarrow{\nabla}\Phi_{4}d\omega & \int_{\Omega}\overrightarrow{\nabla}\Phi_{4}.\overrightarrow{\nabla}\Phi_{4}d\omega \end{array}\right]\end{split}\]

\[\begin{split}\mathbf{X}=\left[\begin{array}{c} \psi_{1}\\ \psi_{2}\\ \psi_{3}\\ \psi_{4} \end{array}\right]\label{c4eq10a}\end{split}\]

\[\begin{split}\mathbf{B}=-\psi^{e}\left[\begin{array}{c} \sum_{j=5}^{7}\int_{\Omega}\overrightarrow{\nabla}\Phi_{j}.\overrightarrow{\nabla}\Phi_{1}d\omega\\ \sum_{j=5}^{7}\int_{\Omega}\overrightarrow{\nabla}\Phi_{j}.\overrightarrow{\nabla}N_{2}d\omega\\ \sum_{j=5}^{7}\int_{\Omega}\overrightarrow{\nabla}\Phi_{j}.\overrightarrow{\nabla}\Phi_{3}d\omega\\ \sum_{j=5}^{7}\int_{\Omega}\overrightarrow{\nabla}\Phi_{j}.\overrightarrow{\nabla}\Phi_{4}d\omega \end{array}\right]\end{split}\]

soit sous forme générique:

(6.20)\[\begin{split}\begin{aligned} \mathbf{A}_{ij}=\int_{\Omega}\left(\frac{\partial\Phi_{j}}{\partial x}\frac{\partial\Phi_{i}}{\partial x}+\frac{\partial\Phi_{j}}{\partial y}\frac{\partial\Phi_{i}}{\partial y}\right)dxdy & i=1,4 & j=1,4 \\ \mathbf{B}_{i}=-\sum_{j=5}^{7}\psi^{e}\int_{\Omega}\left(\frac{\partial\Phi_{j}}{\partial x}\frac{\partial\Phi_{i}}{\partial x}+\frac{\partial\Phi_{j}}{\partial y}\frac{\partial\Phi_{i}}{\partial y}\right)dxdy & i=1,4\end{aligned}\end{split}\]

On remarque que la matrice \(\mathbf{A}\) est symétrique due à la symétrie de la formulation faible.

La recherche d’une solution approchée par éléments finis dans la formulation faible se ramène donc à la résolution du système linéaire (6.20). Il nous reste donc à calculer la matrice \(\mathbf{A}\) et le second membre \(\mathbf{B}\). A nouveau, comme dans le chapitre précédent, nous n’allons pas calculer directement les intégrales dans les relations (6.20), mais suivre une approche systématique pour le calcul de \(\mathbf{A}\) et \(\mathbf{B}\)

6.1.4.1. assemblage de la matrice

Le calcul des coefficients de \(\mathbf{A}\) se fait élément par élément, en notant que l’intégrale sur le domaine \(\Omega\) est la somme d’intégrales élémentaires sur chacun des triangles \(e_{k}\) du maillage:

\[\mathbf{A}_{ij}=\sum_{k=1}^{ne}\int_{e_{k}}\left(\frac{\partial\Phi_{j}}{\partial x}\frac{\partial\Phi_{i}}{\partial x}+\frac{\partial\Phi_{j}}{\partial y}\frac{\partial\Phi_{i}}{\partial y}\right)dxdy=\sum_{l=1}^{ne}A_{ij}^{k}\]

En utilisant la propriété des fonctions de base \(N_{i}\) qui sont non nulles uniquement sur le support du noeud i, on constate que les intégrales élémentaires \(A_{ij}^{k}\) sont presque toujours nulles sauf si l’élément \(e_{k}\) est dans le support du noeud i et du noeud j, c’est à dire si i et j sont des sommets de l’élément \(e_{l}\).

On a donc en réalité \(3*3=9\) intégrales élémentaires à calculer par élément \(e_{k}\), ce sont, en notant \(\{n_{1},n_{2},n_{3}\}\) les numéros des 3 sommets de l’élément k:

(6.21)\[\mathbf{A}_{pq}^{k}=\int_{e_{k}}\left(\frac{\partial\Phi_{n_{p}}}{\partial x}\frac{\partial\Phi_{n_{q}}}{\partial x}+\frac{\partial\Phi_{n_{p}}}{\partial y}\frac{\partial\Phi_{n_{q}}}{\partial y}\right)dxdy\,\,\mbox{ pour }p=1,3\,q=1,3\]

Avec ces notations, le premier coefficient de la matrice \(\mathbf{A}\) s’écrit

\[\mathbf{A}_{11}=\mathbf{A}_{11}^{1}+\mathbf{A}_{33}^{2}+\mathbf{A}_{33}^{3}+\mathbf{A}_{11}^{4}+\mathbf{A}_{33}^{5}+\mathbf{A}_{11}^{6}\]

puisque le noeud 1 a pour support les éléments \(\{e_{1},e_{2},e_{3},e_{4},e_{5},e_{6}\}\) et correspond au premier sommet sur l’élément \(e_{1}\), au troisième sur \(e_{2}\), …. De même le second coefficient de \(\mathbf{A}\) s’écrit:

\[\mathbf{A}_{12}=\mathbf{A}_{31}^{5}+\mathbf{A}_{13}^{6}\]

puisque les seuls éléments ayant comme sommet les noeuds 1 et 2 sont les éléments \(\{e_{5},e_{6}\}\). Sur l’élément \(e_{5}\) le noeud 1 correspond au troisième sommet et le noeud 2 au premier, alors que sur l’élément \(e_{6}\) le noeud 1 correspond au premier sommet et le noeud 2 au troisième.

L’assemblage complet de la matrice \(\mathbf{A}\) donne donc:

(6.22)\[\begin{split}\mathbf{A}=\left[\begin{array}{cccc} A_{11}^{1}+A_{33}^{2}+A_{33}^{3}+ & A_{31}^{5}+A_{13}^{6} & 0 & 0\\ A_{11}^{4}+A_{33}^{5}+A_{11}^{6}\\ A_{13}^{5}+A_{31}^{6} & A_{11}^{5}+A_{33}^{6}+A_{22}^{7}+A_{11}^{8} & A_{23}^{7}+A_{13}^{8} & 0\\ \\ 0 & A_{32}^{7}+A_{31}^{8} & A_{33}^{7}+A_{33}^{8}+A_{33}^{9}+ & A_{33}^{10}+A_{12}^{12}\\ & & A_{32}^{10}+A_{11}^{11}+A_{11}^{12}\\ 0 & 0 & A_{23}^{10}+A_{21}^{12} & A_{22}^{10}+A_{22}^{12} \end{array}\right]\end{split}\]

Pour calculer les intégrales élémentaires (6.21), on effectue la transformation vers l’élément de référence.

Pour calculer l’intégrale d’une fonction \(f(x,y)\) sur un élément \(e_{k}\), on effectue le changement de variable \(x=x(\xi,\eta)\) et \(y=y(\xi,\eta)\) pour se ramener à un calcul d’intégrale sur l’élément de référence. Le calcul de cette intégrale sur l’élément de référence s’effectue par partie, en intégrant d’abord en \(\eta\) puis en \(\xi\). On a donc:

\[\int_{e_{k}}f(x,y)\,dxdy=\int_{0}^{1}\int_{0}^{1-\xi}f(\xi,\eta)\,\det(\mathbf{J}_{k})\,d\eta d\xi\]

puisque l’on a la relation suivante entre les éléments de surface:

\[dxdy=\det(\mathbf{J}_{k})\,d\xi d\eta\]

où \(\mathbf{J}_{k}\) est le jacobien (6.13) de la transformation \(T_{k}^{-1}\) de l’élément de référence \(\hat{e}\) vers l’élément \(e_{l}\) vers . En utilisant la relation (6.16) pour le calcul des dérivées, la matrice élémentaire s’écrit après ce changement de variable:

(6.23)\[\begin{split}\mathbf{A}_{pq}^{k}=\int_{0}^{1}\left[\int_{0}^{1-\xi}\left((\mathbf{J}_{k}^{-1})^{t}\left[\begin{array}{c} \frac{\partial N_{p}}{\partial\xi}\\ \frac{\partial N_{p}}{\partial\eta} \end{array}\right]\right)^{t}.\left((\mathbf{J}_{k}^{-1})^{t}\left[\begin{array}{c} \frac{\partial N_{q}}{\partial\xi}\\ \frac{\partial N_{q}}{\partial\eta} \end{array}\right]\right)\det(\mathbf{J}_{k})\,d\eta\right]d\xi\end{split}\]

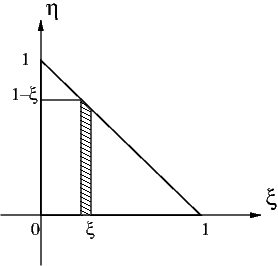
Fig. 6.9 Intégration sur l’élément de référence

En notant que la matrice jacobienne \(\mathbf{J}_{k}\) est constante ainsi que les gradients des fonctions de forme, et que la surface de l’élément de référence vaut:

\[\int_{0}^{1}\int_{0}^{1-\xi}d\eta d\xi=\mbox{ aire du triangle }=\frac{1}{2},\]

l’intégrale se simplifie:

(6.24)\[\begin{split}\mathbf{A}_{pq}^{k}=\frac{\det(\mathbf{J}_{k})}{2}\left[\begin{array}{cc} \frac{\partial N_{p}}{\partial\xi} & \frac{\partial N_{p}}{\partial\eta}\end{array}\right](\mathbf{J}_{k}^{-1}).(\mathbf{J}_{k}^{-1})^{t}\left[\begin{array}{c} \frac{\partial N_{q}}{\partial\xi}\\ \frac{\partial N_{q}}{\partial\eta} \end{array}\right]\end{split}\]

Un calcul directe du déterminant du Jacobien fournit la valeur:

\[\det(\mathbf{J}^{k})=2\,aire_{k}\]

que l’on peut vérifier en notant que ce déterminant est le rapport entre l’aire du triangle \(e_{k}\) : \(aire_{k}\), et l’aire du triangle de référence \(\hat{e}\) : \(1/2\) et. De même par un calcul directe le produit matriciel \((\mathbf{J}_{k}^{-1}).(\mathbf{J}_{k}^{-1})^{t}\) s’écrit:

\[\begin{split}(\mathbf{J}_{k}^{-1}).(\mathbf{J}_{k}^{-1})^{t}=\frac{1}{(2aire_{k})^{2}}\left[\begin{array}{cc} (x_{3}^{k}-x_{1}^{k})^{2}+(y_{3}^{k}-y_{1}^{k})^{2} & (x_{3}^{k}-x_{1}^{k})(x_{1}^{k}-x_{2}^{k})+\\ & (y_{3}^{k}-y_{1}^{k})(y_{1}^{k}-y_{2}^{k})\\ (x_{3}^{k}-x_{1}^{k})(x_{1}^{k}-x_{2}^{k})+ & (x_{1}^{k}-x_{2}^{k})^{2}+(y_{1}^{k}-y_{2}^{k})^{2}\\ (y_{3}^{k}-y_{1}^{k})(y_{1}^{k}-y_{2}^{k}) \end{array}\right]\end{split}\]

Compte tenu de l’expression (6.11) des fonctions de forme, le calcul de leur gradient est trivial:

\[\begin{split}\overrightarrow{\nabla}N_{1}=\left[\begin{array}{c} -1\\ -1 \end{array}\right],\,\overrightarrow{\nabla}N_{2}=\left[\begin{array}{c} 1\\ 0 \end{array}\right],\,\overrightarrow{\nabla}N_{3}=\left[\begin{array}{c} 0\\ 1 \end{array}\right]\end{split}\]

Pour calculer la matrice élémentaire, on peut effectuer le calcul directe des 9 coefficients à partir de la relation (6.24), mais on peut aussi remarquer que la matrice élémentaire est symétrique, et que la somme des lignes (et des colonnes) est nulle (car la somme des gradients des fonctions de forme est nulle). Il suffit donc de calculer 3 coefficients: \(A_{22}^{k},\,A_{33}^{k},\,A_{23}^{k}\) , les autres étant déduits comme indiqué ci dessous:

(6.25)\[\begin{split}\mathbf{A}^{k}=\left[\begin{array}{ccc} \mathbf{A}_{22}^{k}+\mathbf{A}_{33}^{k}+2\mathbf{A}_{23}^{k} & -\mathbf{A}_{23}^{k}-\mathbf{A}_{22}^{k} & -\mathbf{A}_{23}^{k}-\mathbf{A}_{33}^{k}\\ -\mathbf{A}_{23}^{k}-\mathbf{A}_{22}^{k} & \mathbf{A}_{22}^{k} & \mathbf{A}_{23}^{k}\\ -\mathbf{A}_{23}^{k}-\mathbf{A}_{33}^{k} & \mathbf{A}_{23}^{k} & \mathbf{A}_{33}^{k} \end{array}\right]\end{split}\]

Le calcul de ces 3 coefficients donne

(6.26)\[\begin{split}\begin{aligned} \mathbf{A}_{22}^{k}=\frac{(x_{3}^{k}-x_{1}^{k})^{2}+(y_{3}^{k}-y_{1}^{k})^{2}}{4aire_{k}},\,\,\mathbf{A}_{33}^{k}=\frac{(x_{1}^{k}-x_{2}^{k})^{2}+(y_{1}^{k}-y_{2}^{k})^{2}}{4aire_{k}},\\ \mathbf{A}_{23}^{k}=\frac{(x_{3}^{k}-x_{1}^{k})(x_{1}^{k}-x_{2}^{k})+(y_{3}^{k}-y_{1}^{k})(y_{1}^{k}-y_{2}^{k})}{4aire_{k}}\end{aligned}\end{split}\]

d’où l’expression de la matrice élémentaire \(\mathbf{A}^{k}\):

(6.27)\[\begin{split}\frac{1}{4aire_{k}}\left[\begin{array}{ccc} (x_{2}^{k}-x_{3}^{k})^{2}+(y_{2}^{k}-y_{3}^{k})^{2} & (x_{2}^{k}-x_{3}^{k})(x_{3}^{k}-x_{1}^{k})+ & (x_{2}^{k}-x_{3}^{k})(x_{1}^{k}-x_{2}^{k})+\\ & (y_{2}^{k}-y_{3}^{k})(y_{3}^{k}-y_{1}^{k}) & (y_{2}^{k}-y_{3}^{k})(y_{1}^{k}-y_{2}^{k})\\ (x_{2}^{k}-x_{3}^{k})(x_{3}^{k}-x_{1}^{k})+ & (x_{3}^{k}-x_{1}^{k})^{2}+(y_{3}^{k}-y_{1}^{k})^{2} & (x_{3}^{k}-x_{1}^{k})(x_{1}^{k}-x_{2}^{k})+\\ (y_{2}^{k}-y_{3}^{k})(y_{3}^{k}-y_{1}^{k}) & & (y_{3}^{k}-y_{1}^{k})(y_{1}^{k}-y_{2}^{k})\\ (x_{2}^{k}-x_{3}^{k})(x_{1}^{k}-x_{2}^{k})+ & (x_{3}^{k}-x_{1}^{k})(x_{1}^{k}-x_{2}^{k})+ & (x_{1}^{k}-x_{2}^{k})^{2}+(y_{1}^{k}-y_{2}^{k})^{2}\\ (y_{2}^{k}-y_{3}^{k})(y_{1}^{k}-y_{2}^{k}) & (y_{3}^{k}-y_{1}^{k})(y_{1}^{k}-y_{2}^{k}) \end{array}\right]\end{split}\]

Exercice: retrouver ce résultat en utilisant l’expression des fonctions d’interpolation dans le plan physique (x,y).

Pour calculer la matrice de notre système, il suffit donc de calculer les 11 matrices élémentaires correspondants aux \(Ne=11\) éléments du maillage en utilisant les relations (6.25) et (6.26), et de reporter les coefficients dans la matrice globale (6.22).

On obtiens ainsi les valeurs des coefficients de la matrice du système:

(6.28)\[\begin{split}\mathbf{A}=\left[\begin{array}{cccc} 0.5938 & -0.25 & 0.0 & 0.0\\ -0.25 & 36.5 & -16.0 & 0.0\\ 0.0 & -16.0 & 40.0 & -16.0\\ 0.0 & 0.0 & -16.0 & 32.0 \end{array}\right]\end{split}\]

qui est bien entendu symétrique.

6.1.4.2. assemblage du second membre

Le calcul du second membre (6.20) procède de la même démarche. On remarque aussi que, dans notre cas, le second membre ne contient que des termes provenant des conditions aux limites. L’intégrale à calculer est exactement la même que pour la matrice \(\mathbf{A}\), et on écrit donc le second membre sous la forme:

\[\mathbf{B}_{i}=-\sum_{j=5}^{7}\psi^{e}\left(\sum_{k=1}^{ne}\int_{_{e_{k}}}\left(\frac{\partial\Phi_{j}}{\partial x}\frac{\partial\Phi_{i}}{\partial x}+\frac{\partial\Phi_{j}}{\partial y}\frac{\partial\Phi_{i}}{\partial y}\right)dxdy\right)\]

C’est la somme de coefficients de matrices élémentaires \(\mathbf{A}_{pq}^{k}\) (6.21): pour calculer le second membre \(\mathbf{B}_{i}\), on doit prendre en compte les matrices élémentaires des éléments du maillage ayant le noeud \(i\) comme sommet et un des noeuds \(j\) sur le bord \(EF\) (i.e. \(j=5,6,7\)). Ainsi pour le second membre \(\mathbf{B}_{1}\) on a:

\[\mathbf{B}_{1}=-\mathbf{A}_{13}^{4}\psi_{7}-\mathbf{A}_{12}^{4}\psi_{6}-\mathbf{A}_{32}^{5}\psi_{6}=-\mathbf{A}_{13}^{4}\psi_{e}-\mathbf{A}_{12}^{4}\psi_{e}-\mathbf{A}_{32}^{5}\psi_{e}\]

puisque que l’élément \(e_{4}\) a pour premier sommet le noeud 1 et pour troisième sommet le noeud 7 (qui sur \(EF),\) mais aussi pour second sommet le noeud 6 (qui sur \(EF),\) et que l’élément \(e_{5}\) a pour troisième sommet le noeud 1 et pour second sommet le noeud 6.

Le second membre complet s’écrit donc:

\[\begin{split}\mathbf{B}=\left[\begin{array}{c} -\mathbf{A}_{13}^{4}\psi_{e}-\mathbf{A}_{12}^{4}\psi_{e}-\mathbf{A}_{32}^{5}\psi_{e}\\ -\mathbf{A}_{12}^{5}\psi_{e}-\mathbf{A}_{21}^{7}\psi_{e}\\ -\mathbf{A}_{31}^{7}\psi_{e}-\mathbf{A}_{12}^{11}\psi_{e}-\mathbf{A}_{13}^{11}\psi_{e}-\mathbf{A}_{13}^{12}\psi_{e}\\ -\mathbf{A}_{23}^{12}\psi_{e} \end{array}\right]\end{split}\]

Le calcul précédent nous a fournit les matrices élémentaires, et on obtiens comme valeurs de \(\mathbf{B}\) :

(6.29)\[\begin{split}\mathbf{B}=\left[\begin{array}{c} 0.0156\\ 10.25\\ 4.0\\ 8.0 \end{array}\right]\end{split}\]

compte tenue de la valeur de \(\psi_{e}=1.0\)

6.1.4.3. résolution

La résolution du système linéaire avec la matrice (6.28) et le second membre (6.29) , nous fournit la valeur de la solution approchée pour les 4 degrés de liberté du système:

\[\begin{split}X=\left[\begin{array}{c} 0.2377\\ 0.5021\\ 0.5010\\ 0.5005 \end{array}\right]\end{split}\]

Compte tenu des conditions aux limites, on obtiens la solution approchée sur tous les noeuds du maillage:

\[\psi_{e}=\left[\begin{array}{ccccccccccc} 0.2377 & 0.5021 & 0.5010 & 0.5005 & 1.0 & 1.0 & 1.0 & 0.0 & 0.0 & 0.0 & 0.0\end{array}\right]\]

Cette solution est représentée sur la figure suivante sous la forme d’iso-valeurs en couleur. Une ligne \(\psi=cste\) corresponds à une couleur fixe, dont la valeur est fournit par la palette de couleurs à droite de la figure. Ces lignes iso-valeurs \(\psi=cste\) sont justement les lignes de courant de l’écoulement . Compte tenu de la petitesse du maillage, ces lignes de courant approchées ne sont pas très régulières, mais on retrouve le comportement global de l’écoulement qui est défléchi par l’obstacle.

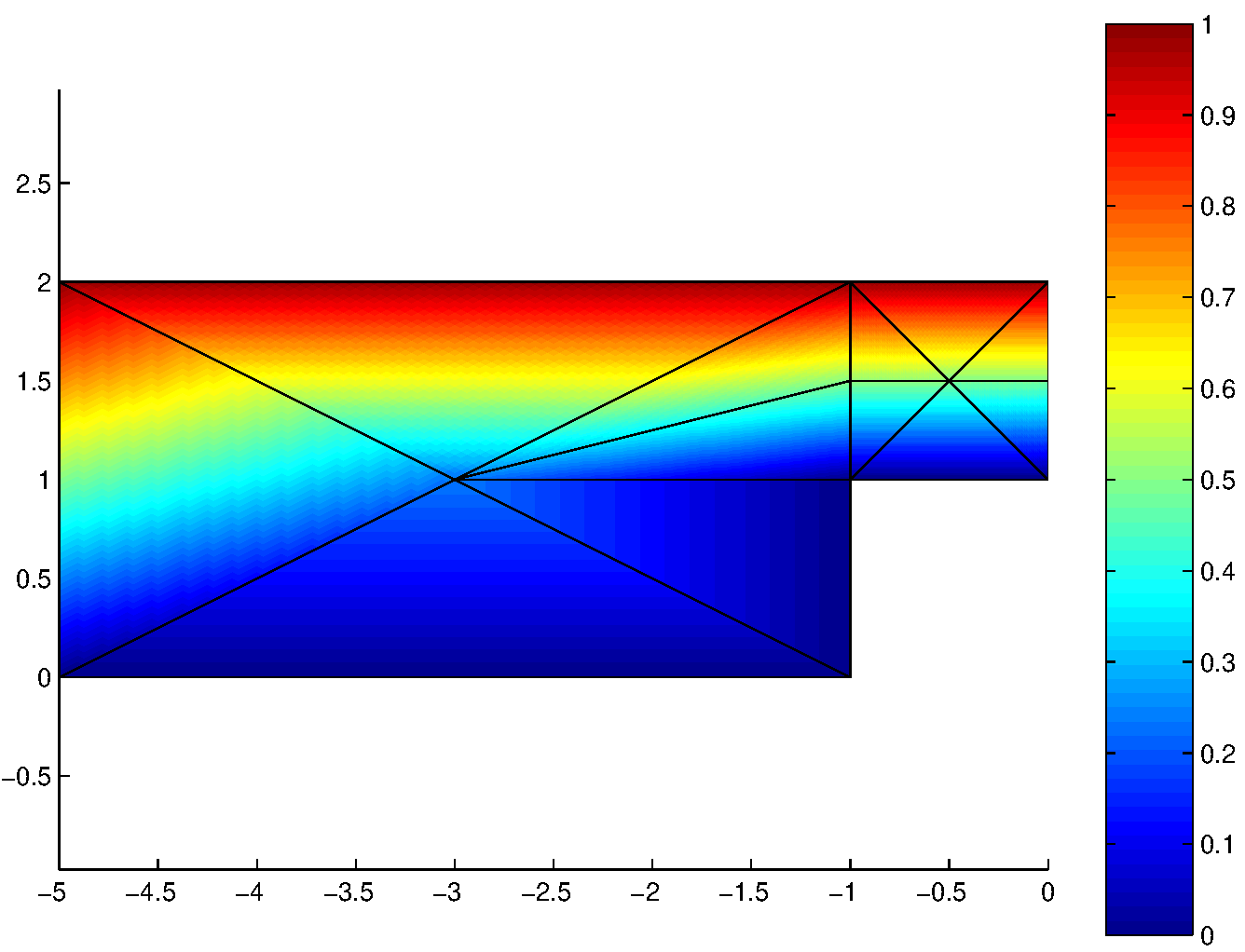
Fig. 6.10 Iso-valeurs de la solution approchée

On peut comparer cette solution à la solution calculée sur un maillage beaucoup plus fin de \(3200\) éléments et \(1691\) noeuds. Les iso-valeurs de cette solution, qui est très proche de la solution exacte sont tracées sur la figure ci-dessous.

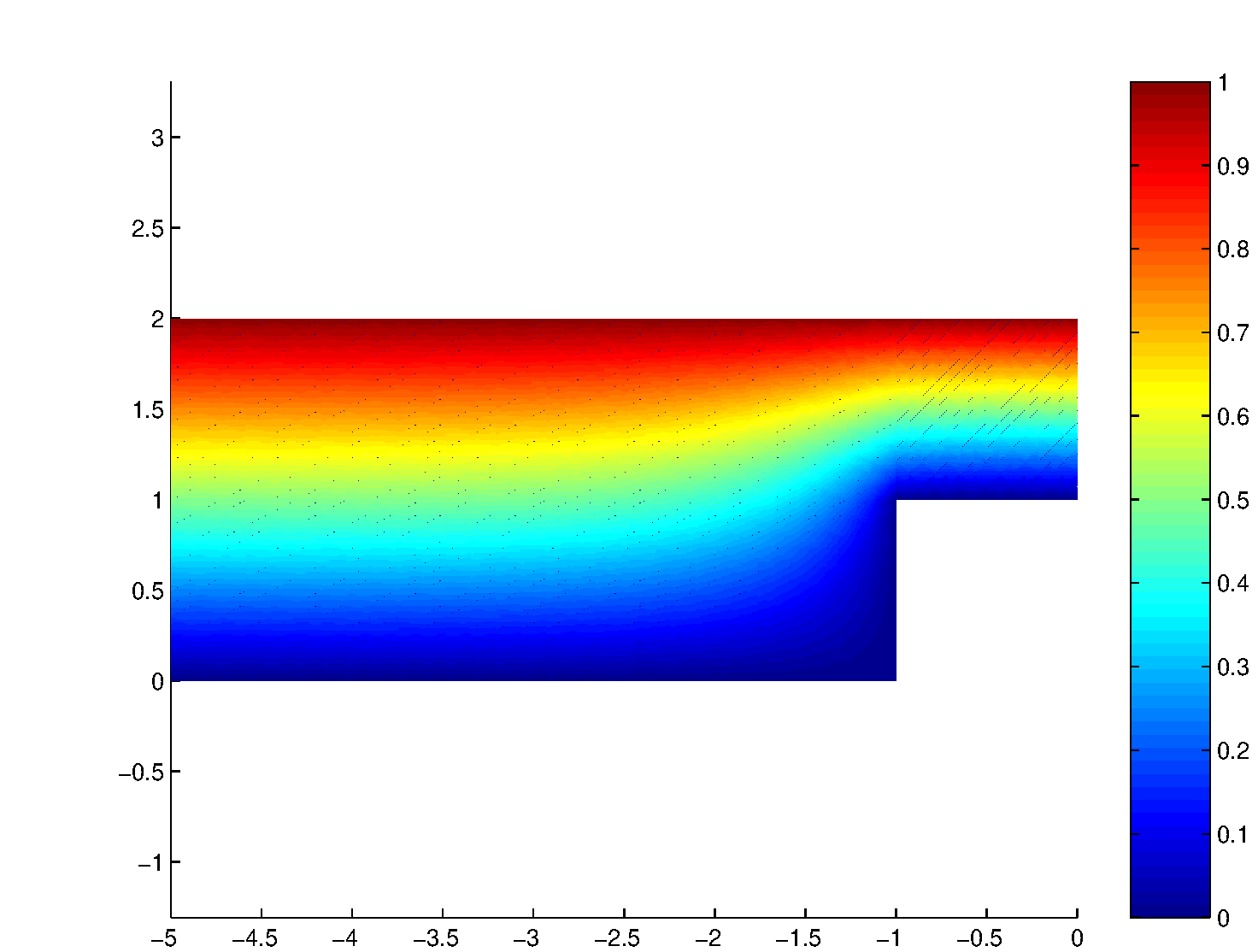
Fig. 6.11 Iso-valeurs de la solution sur un maillage très fin

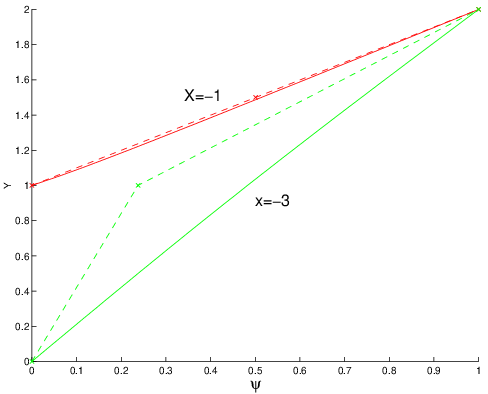
Fig. 6.12 Comparaison des profils calculés (x) avec les profils de référence

En comparant les deux figures, on constate que l’allure de l’écoulement est bien la même, par contre la déviation des lignes de courants sur le maillage grossier est beaucoup trop importante en amont de l’obstacle, comparée à la solution de référence. Par contre sur l’obstacle, la solution est quasiment identique et correspond à une répartition linéaire. Cela est confirmé par la figure suivante, où on a tracé les profils de la solution approchée (en traits pointillés) pour deux abscisses \(x=-1\) (droit de l’obstacle) et \(x=-3\) (amont de l’obstacle), comparés à la solution de référence (en traits pleins).

6.2. Éléments finis triangulaire \(\mathcal{P}^{1}\)

Après l’étude du paragraphe précédent, nous allons maintenant étudier l’approximation par éléments finis \(\mathcal{P}^{1}\) d’un problème générique sur un domaine bidimensionnel \(\Omega\) quelconque (figure ci-dessous).

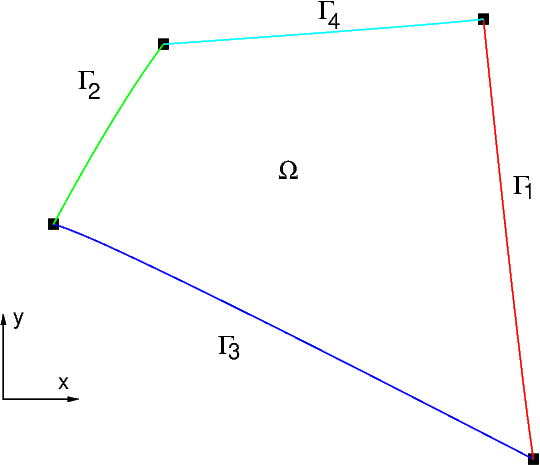
Fig. 6.13 domaine \(\Omega\) de calcul

La frontière \(\Gamma=\partial\Omega\) se décompose en 4 sous frontières disjointes (et éventuellement nulle):

\[\Gamma=\Gamma_{1}\cup\Gamma_{2}\cup\Gamma_{3}\cup\Gamma_{4}\]

Chacune de ses frontières correspond à un type de conditions aux limites appliquées à la solution \(u(x,y):\)

1. \(\Gamma_{1}\) est une frontière de type Dirichlet homogène: i.e. \(u_{\Gamma_{1}}=0,\)

2. \(\Gamma_{2}\) est une frontière de type Dirichlet non-homogène: i.e. \(u_{\Gamma_{2}}=u_{e},\)

3. \(\Gamma_{3}\) est une frontière de type Neuman homogène: i.e. \((\frac{\partial u}{\partial n})_{\Gamma_{3}}=0,\)

4. \(\Gamma_{4}\) est une frontière de type Fourier: i.e. \(-K\,(\frac{\partial u}{\partial n})_{\Gamma_{4}}=\beta u_{\Gamma_{4}}+\phi_{0}\).

Le problème générique que nous allons étudier s’écrit alors:

(6.30)\[\begin{split}\left\{ \begin{array}{cc} -\frac{\partial}{\partial x}\left(K\frac{\partial u}{\partial x}\right)-\frac{\partial}{\partial y}\left(K\frac{\partial u}{\partial y}\right)+\alpha\,u(x,y)=f(x,y)\,\,\mbox{sur\, }\,\Omega\\ u_{\Gamma_{1}}=0,\,u_{\Gamma_{2}}=u_{e},\,(\frac{\partial u}{\partial n})_{\Gamma_{3}}=0,\,-K\,(\frac{\partial u}{\partial n})_{\Gamma_{4}}=\beta u_{\Gamma_{4}}+\phi_{0} \end{array}\right.\end{split}\]

L’équation d’équilibre est une équation de convection-conduction avec un terme source fonction de la solution. \(K\) représente le coefficient de diffusion \((K>0)\), \(\alpha\) le coefficient du terme source \((\alpha\ge0)\) linéaire en \(u(x,y)\), et \(f(x,y)\) le terme source indépendant de \(u(x,y)\).

6.2.1. Formulation faible

La formulation faible de (6.30) s’obtiens comme toujours en multipliant par une fonction test \(v(x,y),\) puis en intégrant sur le domaine \(\Omega\). On intègre ensuite par partie le terme en dérivée seconde en utilisant la formule de Green. En utilisant les conditions aux limites et en interprétant la fonction test \(v(x,y)\) comme une variation \(\delta u\) de la solution \(u(x,y)\), la formulation faible s’écrit:

(6.31)\[\begin{split}\left\{ \begin{array}{cc} \mbox{Trouver }\,u(x,y)\,\mbox{ t.q. }\,u_{\Gamma_{1}}=0,\,u_{\Gamma_{2}}=u_{e}\\ \int_{\Omega}K(\frac{\partial u}{\partial x}\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}\frac{\partial v}{\partial y})\,d\omega+\int_{\Omega}\alpha u.v\,d\omega+\int_{\Gamma_{4}}\beta u.v\,d\gamma=\int_{\Omega}fv\,d\omega-\int_{\Gamma_{4}}\phi_{0}v\,d\gamma\\ \forall\,v(x,y)\,\mbox{ t.q. }\,v_{\Gamma_{1}}=0,\,v_{\Gamma_{2}}=0 \end{array}\right.\end{split}\]

Pour calculer la solution approchée \(u^{h}\), nous avons besoin d’un maillage de \(\Omega\), et d’une approximation de la solution sur ce maillage.

6.2.2. Maillage éléments finis et interpolation \(\mathcal{P}^{1}\)

Le domaine de calcul \(\Omega\) est découpé en triangles comme sur la figure suivante. Ce maillage est construit à l’aide d’outils informatiques ou de logiciels spécialisés. On trouvera en annexe les outils de maillage, qui nous ont servi à générer les différents maillages utilisés dans ce livre.

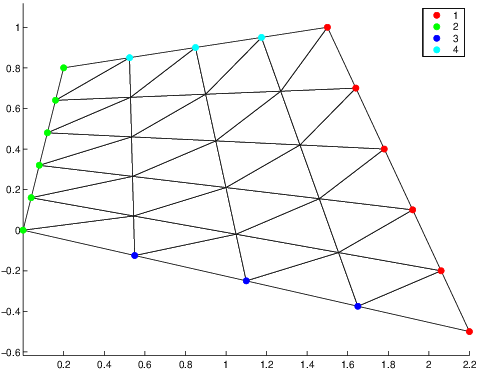
Fig. 6.14 Maillage éléments finis \(\mathcal{P}^{1}\)

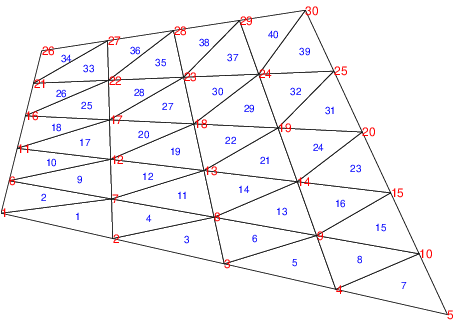
Fig. 6.15 Numérotation sur le maillage éléments finis \(\mathcal{P}^{1}\)

De façon général, un outil de maillage doit fournir les informations suivantes:

1. le nombre de noeuds nn, le nombre d’éléments ne,

2. les coordonnées \((x_{i},y_{i})\) de chaque noeud \(M_{i}\) du maillage,

3. les numéros des sommets de chaque élément \(e_{k}\) (ou table de connection): \(tbc_{k,1},\,tbc_{k,2}\,,tbc_{k,3}\)

4. pour chaque noeud \(M_{i}\), une information (i.e. un entier) \(frt_{i}\) qui précise si le noeud est interne (\(frt_{i}=0\)), ou sur une frontière \(\Gamma_{l}\) (\(frt_{i}=l\))

5. pour chaque élément \(e_{k}\), une information de région \(reg_{k}\), indiquant le numéro du domaine auquel appartiens l’élément. Par défaut il n’y a qu’un seul domaine et \(reg_{k}=1\) pour tous les éléments.

Avec les outils utilisés, ses informations sont stockés sous forme de tableau dans un fichier de géométrie, ayant par convention une extension .msh. Ce fichier est écrit en ASCII, et est donc lisible sur n’importe quel système et avec n’importe quel langage. Il est compatible avec le format utilisé par FREEFEM[2], un logiciel éléments finis du domaine public. Le fichier de maillage est structuré par ligne de la façon suivante:

Tableau 6.3 Fichier de maillage (type msh)

ligne	champ 1	champ 2	champ 3	champ 4
\(1\)	\(nn\)	\(ne\)	« comment »
\(2\)	\(x_{1}\)	\(y_{1}\)	\(frt_{1}\)
\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)
\(nn+1\)	\(x_{nn}\)	\(y_{nn}\)	\(frt_{nn}\)
\(nn+2\)	\(tbc_{1,1}\)	\(tbc_{1,2}\)	\(tbc_{1,3}\)	\(reg_{1}\)
\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)
\(nn+ne+1\)	\(tbc_{ne,1}\)	\(tbc_{ne,2}\)	\(tbc_{ne,3}\)	\(reg_{ne}\)

Le fichier de maillage de la figure précédente est accessible ici fichier maillage.msh.

En programmation, nous utiliserons une structure de données pour la géométrie de type structure, qui contiendra les champs suivants (en notant G le nom variable géométrie):

G.nn : nbre de noeuds de la géométrie G : entier

G.ne : nbre d’éléments de la géométrie G : entier

G.dim : la dimension d’espace (=2 en 2D) : entier

G.ddl : nbre de degré de liberté par éléments (=3 pour des éléments \(\mathcal{P}^{1}\) en 2D) : entier

G.X : tableau des coordonnées \((x,y)\) des noeuds: tableau \(G.nn*G.dim\) réels

G.Tbc : table de connection: tableau \(G.ne*G.ddl\) entiers

G.Frt : numéro de frontière par noeuds: tableau \(G.nn\) entiers

G.Ref : numéro de région par éléments: tableau \(G.ne\) entiers

Le programme Python suivant définit une classe mesh de base pour définir le maillage avec une méthode lecture pour lire une géométrie éléments finis sur fichier passé en argument qui initialise le maillage.

import  numpy as np
# définition structure geometrie
class mesh():
    def __init__(self):
        self.nn=0
        self.ne=0
        self.X=None
        self.Tbc=None
        self.Frt=None
        self.Reg=None
        self.nom=None
        return
	def lecture(self,fichier):
    """ lecture d'un maillage dans un fichier  """
 		self.nom = fichier
    		# lecture maillage EF FreeFem 
    		F = open(fichier,"r")
    		# lecture 1ere ligne
    		L = F.readline().split()
    		F = open(fichier,"r")
    		# lecture 1ere ligne
    		L = F.readline().split()
    		# extraction nbre de nds et nbre d'elements
	    self.nn = int(L[0])
    		self.ne = int(L[1])
    		# boucle lecture des coordonnées
    		self.X=np.zeros((self.nn,2))
    		self.Frt=np.zeros(self.nn,dtype=int)
    		for i in range(self.nn):
        		L=F.readline().split()
        		self.X[i,0]=float(L[0])
        		self.X[i,1]=float(L[1])
        		self.Frt[i]=int(L[2])
    		# et de la table de connexion
    		self.Tbc=np.zeros((self.ne,3),dtype=int)
    		for k in range(self.ne):
        		L=F.readline().split()
        		for i in range(3):
            		self.Tbc[k,i] = int(L[i]) - 1
    		#
    		F.close()
    		return 

Dans ce programme, on a modifié la table de connexion Tbc en retranchant 1 pour tenir compte du fait qu’en Python, les tableaux ont un indice qui commence à zéro et non un.

Ensuite, pour lire la géométrie stockée dans le fichier maillage.msh, on écrit simplement:

G = mesh()
G.lecture("maillage.msh")

6.2.2.1. Approximation éléments finis

On a montré précédemment qu’une approximation \(u^{h}(x,y)\) sur un maillage éléments finis est une combinaison linéaire des valeurs nodales \(\{u_{i}\}_{i=1,nn}\) sur les noeuds du maillage. les coefficients de cette combinaison linéaire sont les fonctions de base \(\Phi_{i}(x,y)\) :

\[u^{h}(x,y)=\sum_{i=1}^{nn}u_{i}\,\Phi_{i}(x,y)\,\,\mbox{ avec }\,u_{i}=u^{h}(x_{i},y_{i})\]

Ces fonctions \(\{\Phi_{i}\}\) forment une base locale, i.e. une fonction \(\Phi_{i}(x,y)\) est non nulle uniquement sur une petite partie du maillage: le support du noeud \(M_{i}\), i.e. l’ensemble des éléments \(e_{l}\) ayant le noeud \(M_{i}\) comme sommet (\(M_{i}\in e_{l}\)). Elles vérifient en outre les propriétés suivantes:

1. la fonction de base \(\Phi_{i}(x,y)\) vaut 1 au noeud i et 0 sur tous les autres noeuds:
   $\(\Phi_{i}(x_{j},y_{j})=\delta_{ij}\)$

2. la fonction de base \(\Phi_{i}(x,y)\) est non nulle uniquement sur son support \(Sup_{i}=\{\cup e_{k}\,/M_{i}\in e_{k}\}\)
   $\(N_{i}(x,y)\neq0\,{ si }\,(x,y)\in Sup_{i}\)$

3. la fonction de base \(\Phi_{i}(x,y)\) est orthogonale à presque toutes les autres fonctions de base \(\Phi_{j}\), en particulier celles qui sont associées à des noeuds j non voisin de i (t.q.\(Sup_{i}\cap Sup_{j}=\emptyset\)) :
   $\(\Phi_{i}(x,y)*\Phi_{j}(x,y)\,\left\{ \begin{array}{cc} =0 & \mbox{ si }\,Sup_{i}\cap Sup_{j}=\emptyset\\ =0 & \mbox{ si }\,(x,y)\notin(Sup_{i}\cap Sup_{j})\\ \neq0 & \mbox{ si }\,(x,y)\in(Sup_{i}\cap Sup_{j}) \end{array}\right.\)$

Un exemple de fonctions de base (associées aux noeuds \(7,12,24\) du maillage) est tracé sur la figure Fig. 6.16, ainsi que leurs supports. On constate sur cette figure que les fonctions de base \(\Phi_{7}\) et \(\Phi_{24}\) sont orthogonales (i.e. le produit \(\Phi_{7}*\Phi_{24}\) est toujours nul), ainsi que \(\Phi_{12}\) et \(\Phi_{24}\) , et que le produit \(\Phi_{7}*\Phi_{12}\) est non nul uniquement sur les 2 éléments (\(e_{9},e_{12}\)).

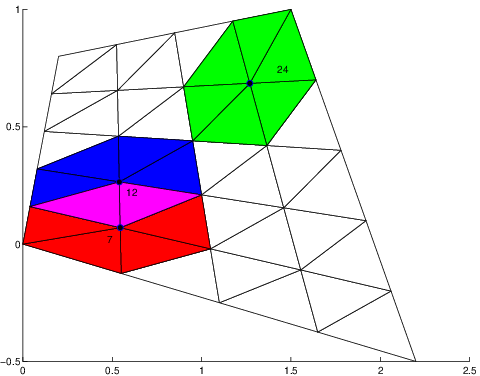
Fig. 6.16 Fonctions de base \(\Phi_{7},\Phi_{12},\Phi_{24}\) et leurs supports

Pour calculer une fonction de base sur un élément \(e_{k}\) du maillage, on utilise une transformation (6.10) (6.12) de cet élément vers un élément de référence \(\hat{e}\) . Sur cet élément de référence, la fonction de base associée à l’un des sommets \(\{S_{q}\}_{q=1,3}\) de l’élément \(e_{k}\) coïncide alors avec l’une des fonctions de forme \(N_{q}(\xi,\eta)\) (6.11) associées aux sommets \(\{\hat{S}_{q}\}\) de l’élément de référence \(\hat{e}\) (6.17).

6.2.3. Formulation faible discrète

La solution approchée \(u^{h}\) de l’équation (6.30) s’écrit sous la forme:

\[u^{h}(x,y)=\sum_{i=1}^{nn}u_{i}\,\Phi_{i}(x,y)\]

Elle doit de plus vérifier les conditions aux limites de Dirichlet, i.e. \(u_{\Gamma_{1}}^{h}=0,\,u_{\Gamma_{2}}^{h}=u_{e}\). Ces conditions de Dirichlet imposent la valeur nodale de \(u^{h}\) sur tous les noeuds se trouvant sur la frontière \(\Gamma_{1}\) ou \(\Gamma_{2}\), i.e:

\[u_{l}=0\,\mbox{\, si\, }\,M_{l}\in\Gamma_{1},\,\,u_{l}=u_{e}\,\mbox{\, si\, }\,M_{l}\in\Gamma_{2}\]

Soit \(nf_{1}\) le nombre de noeuds sur la frontière \(\Gamma_{1}\), et \(nf_{2}\) le nombre de noeuds sur la frontière \(\Gamma_{2}\), le nombre de degré de liberté \(nl\) de \(u^{h}\) est égale à \(nl=nn-nf_{1}-nf_{2}\). Cependant la numérotation du maillage étant quelconque, on ne peut comme dans l’exemple précédent avoir une numérotation simple des degrés de liberté. En notant \(\overline{\Omega}_{d}=\Omega-\Gamma_{1}-\Gamma_{2}\), on écrit la solution sous la forme:

(6.32)\[u^{h}(x,y)=\sum_{j\in\overline{\Omega}_{d}}u_{j}\,\Phi_{j}(x,y)+\sum_{l\in\Gamma_{2}}u_{e}\,\Phi_{l}(x,y)\]

Les fonctions tests associées \(v^{h}(x,y)\) sont des variations de \(u^{h}\), qui doivent donc s’annuller sur les frontières de Dirichlet \(\Gamma_{1}\) et \(\Gamma_{2}\). Elles s’écrivent sous la forme générale suivante:

\[v^{h}(x,y)=\sum_{i\in\overline{\Omega}_{d}}v_{i}\,\Phi_{i}(x,y)\]

Ces fonctions tests sont une combinaison linéaire des \(n_{l}\) fonctions de base \(\Phi_{i}\) (\(i\in\overline{\Omega}_{d}\)). En remplaçant la solution exacte \(u\) par l’expression (6.32) de \(u^{h}\) et la fonction test \(v\) par une des fonctions de base précédentes \(\Phi_{i}\), on obtiens la formulation faible discrète:

(6.33)\[\begin{split}\begin{aligned} \sum_{j\in\overline{\Omega}_{d}}u_{j}\left(\underbrace{\int_{\Omega}K(\frac{\partial\Phi_{j}}{\partial x}\frac{\partial\Phi_{i}}{\partial x}+\frac{\partial\Phi_{j}}{\partial y}\frac{\partial\Phi_{i}}{\partial y})\,d\omega+\int_{\Omega}\alpha\Phi_{j}.\Phi_{i}\,d\omega}_{\mbox{terme générique de}\,A}+\underbrace{\int_{\Gamma_{4}}\beta\Phi_{j}.\Phi_{i}\,d\gamma}_{\mbox{terme C.L. sur A}}\right) & =\nonumber \\ \underbrace{\int_{\Omega}f\Phi_{i}\,d\omega}_{\mbox{terme générique de B}}-\underbrace{\int_{\Gamma_{4}}\phi_{0}\Phi_{i}\,d\gamma}_{\mbox{terme C.L. sur B}} & - \\ \sum_{l\in\Gamma_{2}}u_{l}\underbrace{\left(\int_{\Omega}K(\frac{\partial\Phi_{l}}{\partial x}\frac{\partial\Phi_{i}}{\partial x}+\frac{\partial\Phi_{l}}{\partial y}\frac{\partial\Phi_{i}}{\partial y})\,d\omega+\int_{\Omega}\alpha\Phi_{l}.\Phi_{i}\,d\omega+\int_{\Gamma_{4}}\beta\Phi_{l}.\Phi_{i}\,d\gamma\right)}_{\mbox{terme C.L. sur B }}\end{aligned}\end{split}\]

La relation (6.33) écrite pour les \(nl\) fonctions de base \(N_{i}\) appartenant à \(\overline{\Omega}_{d}\), est un système linéaire de \(nl\) inconnues \(u_{j}\) (\(j\in\overline{\Omega}_{d}\)), qu’il suffit de résoudre pour obtenir la solution approchée \(u^{h}\). Le calcul directe de ce système linéaire nécessiterait une renumérotation des noeuds, de façon à avoir la même numérotation pour les inconnues et degrés de liberté (i.e. de 1 à \(nl\) pour les noeuds \(j\in\overline{\Omega}_{d}\)), et ce chaque fois que l’on change les conditions aux limites du problème. De façon à écrire un programme qui soit le plus général possible, on construira tout d’abord un système linéaire générique pour toutes les valeurs nodales \(\{u_{i}\}_{i=1,nn}\), puis on appliquera les conditions aux limites du problème sur ce système linéaire de dimension \(nn\).

Les coefficients génériques de la matrice \(\mathbf{A}\) et du second membre \(\mathbf{B}\) s’écrivent:

\[\begin{split}\begin{eqnarray} \mathbf{A}_{ij} & = & \int_{\Omega}K(\frac{\partial\Phi_{j}}{\partial x}\frac{\partial\Phi_{i}}{\partial x}+\frac{\partial\Phi_{j}}{\partial y}\frac{\partial\Phi_{i}}{\partial y})\,d\omega+\int_{\Omega}\alpha\Phi_{j}.\Phi_{i}\,d\omega\\ \mathbf{B}_{i} & = & \int_{\Omega}f\Phi_{i}\,d\omega\end{eqnarray}\end{split}\]

Pour calculer ces coefficients, on effectue un calcul élément par élément en déterminant les matrices et les second membres élémentaires sur chaque élément \(e_{k}\):

\[\begin{split}\begin{eqnarray} \mathbf{A}_{ij} & = & \sum_{k=1}^{ne}\left(\underbrace{\int_{e_{k}}K(\frac{\partial\Phi_{j}}{\partial x}\frac{\partial\Phi_{i}}{\partial x}+\frac{\partial\Phi_{j}}{\partial y}\frac{\partial\Phi_{i}}{\partial y})\,d\omega+\int_{e_{k}}\alpha\Phi_{j}.\Phi_{i}\,d\omega}_{\mbox{matrice élémentaire}}\right)\\ \mathbf{B}_{i} & = & \sum_{k=1}^{ne}\left(\underbrace{\int_{e_{k}}f\Phi_{i}\,d\omega}_{\mbox{second membre élémentaire}}\right)\end{eqnarray}\end{split}\]

6.2.4. Calcul des matrices élémentaires \(\mathcal{P}^{1}\)

En tenant compte des propriétés des fonctions de base, sur un élément \(e_{k}\) on doit calculer uniquement \(3*3\) intégrales élémentaires faisant intervenir les 3 fonctions de base associées aux 3 sommets de l’élément. En notant \(\{n_{1},n_{2},n_{3}\}\) les numéros de ces 3 sommets, on a donc à calculer sur un élément \(e_{k}\) la matrice élémentaire \(3*3\) suivante:

\[\mathbf{A}_{pq}^{k}=\int_{e_{k}}K(\frac{\partial\Phi_{n_{q}}}{\partial x}\frac{\partial\Phi_{n_{p}}}{\partial x}+\frac{\partial\Phi_{n_{q}}}{\partial y}\frac{\partial\Phi_{n_{p}}}{\partial y})\,d\omega+\int_{e_{k}}\alpha\Phi_{n_{q}}.\Phi_{n_{p}}\,d\omega\,\,\,(p,q=1,3)\]

En considérant que les coefficients \(K\) et \(\alpha\) sont constants sur l’élément \(e_{k}\), cette matrice est la somme d’une matrice élémentaire de rigidité \(\mathbf{K}^{k}\) et d’une matrice de masse \(\mathbf{M}^{k}\):

\[\mathbf{A}_{pq}^{k}=K\,\mathbf{K}_{pq}^{k}+\alpha\,\mathbf{M}_{pq}^{k}\]

Le calcul de ces 2 matrices s’effectue à l’aide du changement de variables vers l’élément de référence \(\hat{e}\).

6.2.4.1. matrice élémentaire de rigidité

Nous rappelons l’expression générique (6.23) de la matrice de rigidité calculée sur l’élément de référence:

\[\begin{split}\mathbf{K}_{pq}^{k}=\int_{0}^{1}\left[\int_{0}^{1-\xi}\left((\mathbf{J}_{k}^{-1})^{t}\left[\begin{array}{c} \frac{\partial N_{p}}{\partial\xi}\\ \frac{\partial N_{p}}{\partial\eta} \end{array}\right]\right)^{t}.\left((\mathbf{J}_{k}^{-1})^{t}\left[\begin{array}{c} \frac{\partial N_{q}}{\partial\xi}\\ \frac{\partial N_{q}}{\partial\eta} \end{array}\right]\right)\det(\mathbf{J}_{k})\,d\eta\right]d\xi\end{split}\]

Le calcul effectué au paragraphe précédent montre que cette matrice dépend de 3 coefficients (6.31), que l’on peut écrire sous forme vectorielle:

\[\mathbf{K}_{22}^{k}=\frac{\left\Vert \overrightarrow{S_{1}S_{3}}\right\Vert ^{2}}{4aire_{k}},\,\mathbf{K}_{33}^{k}=\frac{\left\Vert \overrightarrow{S_{2}S_{1}}\right\Vert ^{2}}{4aire_{k}},\,\mathbf{K}_{23}^{k}=\frac{\overrightarrow{S_{1}S_{3}}.\overrightarrow{S_{2}S_{1}}}{4aire_{k}},\,\,aire_{k}=\frac{1}{2}\left\Vert \overrightarrow{S_{1}S_{3}}\otimes\overrightarrow{S_{2}S_{1}}\right\Vert\]

que l’on reporte dans l’expression de \(\mathbf{K}^{k}\)

\[\begin{split}\mathbf{K}^{k}=\left[\begin{array}{ccc} K_{22}^{k}+K_{33}^{k}+2K_{23}^{k} & -K_{23}^{k}-K_{22}^{k} & -K_{23}^{k}-K_{33}^{k}\\ -K_{23}^{k}-K_{22}^{k} & K_{22}^{k} & K_{23}^{k}\\ -K_{23}^{k}-K_{33}^{k} & K_{23}^{k} & K_{33}^{k} \end{array}\right]\end{split}\]

En utilisant les notations matricielles, ces formulent se programment très simplement. Dans la classe mesh, on ajoute 2 méthodes pour calculer la surface d’un élément l, et le gradient des fonctions de base sur un élément l.

class mesh:
    """ maillage EF 2D avec numerotation des nds a partir de 0"""
    ...
 	def gradient(self,l):
        """ calcul le gradient des fonctions de forme de l'elt l et l'aire""" 
        p=np.zeros((5),dtype=int)
        n=self.Tbc[l,:]; # numero des sommets de 0 a nn-1
        p[0:3]=n[:]; p[3:5]=n[0:2]; # permutation circulaire
        dX=self.X[np.ix_(p[1:4],[0,1])]-self.X[np.ix_(p[2:5],[0,1])]; # aretes
        Aire=0.5*(dX[0,0]*dX[1,1]-dX[1,0]*dX[0,1]);
        dN=np.array([dX[:,1],-dX[:,0]])/(2*Aire);
        return dN,Aire

    def aire(self,l):
        """ calcul de l'aire de l'element l"""
        n=self.Tbc[l,:];
        S21=self.X[n[0],:]-self.X[n[1],:]
        S13=self.X[n[2],:]-self.X[n[0],:]
        return 0.5*(S13[0]*S21[1]-S13[1]*S21[0])

On utilise la fonction np.ix_ qui permet un adressage indirect simple des tableaux.

La fonction suivante MatriceRigidite implémente sous Python les relations précédentes (en utilisant la méthode gradient de la class mesh définie précédemment).

import numpy as np

def MatRigidite(G,k):
    """ calcul matrice de rigidite sur l'elt k du maillage G """
    dN,Aire=G.gradient(k)
    K22=np.dot(dN[:,1],dN[:,1])*Aire
    K33=np.dot(dN[:,2],dN[:,2])*Aire
    K23=np.ot(dN[:,1],dN[:,2])*Aire
    Ke=np.array([[K22+K33+2*K23, -K23-K22,-K23-K33],
              [-K23-K22     , K22     , K23],
              [-K23-K33     , K23     , K33]])
    return Ke

6.2.4.2. matrice élémentaire de masse

De manière identique, le changement de variable permet d’obtenir l’expression générique de la matrice de masse:

\[\mathbf{M}_{pq}^{k}=\int_{0}^{1}\int_{0}^{1-\xi}N_{q}(\xi,\eta)N_{p}(\xi,\eta)\det(\mathbf{J}_{k})\,d\eta d\xi\]

Sur l’élément de référence, le calcul de cette matrice est simple, puisque le déterminant du jacobien est constant, \(\det(\mathbf{J}^{k})=2\,aire_{k}\) et les fonctions de formes \(L_{q}\) et \(L_{p}\) sont des polynômes très simples en (\(\xi,\eta\)). Compte tenu de l’expression de ces polynômes (6.11)et des propriétés de symétrie, il suffit de calculer 2 intégrales:

\[\int_{0}^{1}\int_{0}^{1-\xi}\eta\xi\,d\eta d\xi=\frac{1}{24},\,\int_{0}^{1}\int_{0}^{1-\xi}\xi^{2}\,d\eta d\xi=\frac{1}{12}\]

En effet les propriétés de symétrie imposent:

\[\int_{0}^{1}\int_{0}^{1-\xi}(N_{1})^{2}\,d\eta d\xi=\int_{0}^{1}\int_{0}^{1-\xi}(N_{2})^{2}\,d\eta d\xi=\int_{0}^{1}\int_{0}^{1-\xi}(N_{3})^{2}\,d\eta d\xi=\int_{0}^{1}\int_{0}^{1-\xi}\xi^{2}\,d\eta d\xi\]

\[\int_{0}^{1}\int_{0}^{1-\xi}N_{1}N_{2}\,d\eta d\xi=\int_{0}^{1}\int_{0}^{1-\xi}N_{1}N_{3}\,d\eta d\xi=\int_{0}^{1}\int_{0}^{1-\xi}N_{2}N_{3}\,d\eta d\xi=\int_{0}^{1}\int_{0}^{1-\xi}\eta\xi\,d\eta d\xi\]

d’où l’expression de la matrice de masse élémentaire:

\[\begin{split}\mathbf{M}^{k}=\frac{aire_{k}}{12}\left[\begin{array}{ccc} 2 & 1 & 1\\ 1 & 2 & 1\\ 1 & 1 & 2 \end{array}\right]\end{split}\]

La fonction MatriceMasse qui calcul cette matrice est donné ci dessous.

import numpy as np

def MatMasse(G,k):
    """ calcul matrice de masse sur l'elt k du maillage G """
    Aire=G.aire(k)
    Me=Aire/12.0*np.array([[ 2, 1 ,1 ],
                        [ 1, 2 ,1 ],
                        [ 1, 1 ,2 ]])
    return Me

6.2.5. Calcul du second membre élémentaire \(\mathcal{P}^{1}\)

Pour chaque élément \(e_{k}\), on a à calculer 3 intégrales élémentaires associées à chacun des 3 sommets de l’élément. Avec les mêmes notations que précédemment, ces intégrales s’écrivent:

\[\mathbf{B}_{p}^{k}=\int_{e_{k}}f.\Phi_{n_{p}}\,d\omega\,\,\,(p=1,3)\]

Pour calculer ces intégrales, on remplace la fonction \(f(x,y)\) par son interpolation \(f^{h}(x,y)\) sur le maillage éléments finis:

\[f^{h}(x,y)=\sum_{i=1}^{nn}f_{i}\,\Phi_{i}(x,y)\]

ce qui permet d’écrire les intégrales sous la forme:

\[\mathbf{B}_{p}^{k}=\sum_{q=1}^{3}f_{n_{q}}\left(\int_{e_{k}}\Phi_{n_{q}}.\Phi_{n_{p}}\,d\omega\right)\,\,\,(p=1,3)\]

puisque sur l’élément \(e_{k}\), l’interpolation \(f^{h}\) de \(f\) s’écrit: \(f^{h}(x,y)=\sum_{q=1}^{3}f_{n_{q}}.N_{n_{q}}(x,y)\).

C’est donc le produit du vecteur \(\mathbf{F}^{k}=[f_{n_{1}},f_{n_{2}},f_{n_{3}}]\) des valeurs nodales par la matrice élémentaire de masse \(\mathbf{M}^{k}\). Le second membre élémentaire s’écrit donc:

\[\begin{split}\mathbf{B}^{k}=\mathbf{M}^{k}\mathbf{F}^{k}=\frac{aire_{k}}{12}\left[\begin{array}{ccc} 2 & 1 & 1\\ 1 & 2 & 1\\ 1 & 1 & 2 \end{array}\right]\left[\begin{array}{c} f_{n_{1}}\\ f_{n_{2}}\\ f_{n_{3}} \end{array}\right]\end{split}\]

La fonction SmbElem qui calcul ce second membre est donné ci dessous.

import numpy as np

def SmbElem(G,k,Fe):
    """calcul le second membre élémentaire pour l'element k"""
    Me = MatMasse(G,k)
    Be = np.ddot(Me,Fe)
    return Be

6.2.6. Assemblage

L’assemblage de la matrice \(\mathbf{A}\) et du second membre \(\mathbf{B}\) consiste à passer en revu les éléments, à calculer les matrices élémentaires de masse et de rigidité ainsi que le second membre élémentaire, puis à mettre ses valeurs aux bons endroits dans la matrice et le second membre globale.

L’algorithme d’assemblage ci dessous donne le principe de l’assemblage.

Algorithm 6.1 (Algorithme d’assemblage en 2D)

1. A = 0

2. B = 00

3. Pour k de 1 à ne faire

4. Ke = \(mathbf{K}^k\),

5. Me = \(mathbf{M}^k\)

6. Be = \(\mathbf{B}^k\)

7. n = Tbc(k,:)

8. pour p de 1 a 3 faire

   1. ni = n[p]

   2. pour q de 1 à 3 faire

      1. nj = n[q]

      2. A[ni,nj] = A[ni,nj] + KKe[p,q] + alphaMe[p,q]

   3. fin q

   4. B[ni] = B[ni] + Be[p] 6 fin p

9. fin k

Le programme ci dessous implémente cet algorithme, en utilisant les notations matricielles qui permettent d’éviter l’écriture de boucles. La fonction Assemblage est donné ci dessous.

import numpy as np

def Assemblage(G,K,alpha,F):
    A = np.zeros((G.nn,G.nn))
    B = np.zeros(G.nn)
    for k in range(G.ne):
        Ke = MatRigidite(G,k)
        Me = MatMasse(G,k)
        ni = G.Tbc[k,:]
        Be = SmbElem(G,k,F[np.ix_(ni)])
        A[np.ix_(ni,ni)] += K*Ke + alpha*Me
        B[np.ix_(ni)]    += Be
    return A,B

6.2.7. Conditions aux limites

L’application des conditions aux limites sur le système linéaire obtenu après l’assemblage dépend du type de conditions aux limites.

6.2.7.1. Conditions de Dirichlet

L’imposition des conditions aux limites de Dirichlet (frontières \(\Gamma_{1}\) et \(\Gamma_{2}\)) consiste à fixer la valeur de la solution aux noeuds \(M_{i}\) se trouvant sur la frontière de Dirichlet (\(\Gamma_{1}\cup\Gamma_{2}\)). Pour cela on remplace simplement dans le système linéaire l’équation \(i\) par l’équation:

\[\begin{split}\begin{aligned} u_{i}=0\, & \mbox{si\, }\,M_{i}\in\Gamma_{1}\\ u_{i}=u_{e} & \mbox{si\, }\,M_{i}\in\Gamma_{2}\end{aligned}\end{split}\]

Dans la matrice \(\mathbf{A}\), cela revient à annuler la ligne \(i\) et à mettre un 1 sur la diagonale, et dans le second membre \(\mathbf{B}\), à remplacer la composante i par 0 ou \(u_{e}\) selon le cas:

\[\mathbf{A}_{ij}=0,\,\mathbf{A}_{ii}=1,\,\mathbf{B}_{i}=0\,\mbox{\, ou\, }\,u_{e}\]

Les termes supplémentaires dues à cette conditions aux limites sont automatiquement pris en compte dans les autres équations.

6.2.7.2. Conditions de Neuman

La condition aux limites de Neuman homogène (frontière \(\Gamma_{3}\)) est déjà prise en compte dans la formulation et ne nécessite pas de modification supplémentaire. Par contre la condition mixte sur la frontière \(\Gamma_{4}\) nécessite le calcul d’intégrales de bords:

(6.34)\[\mathbf{A}_{ij}^{cl}=\int_{\Gamma_{4}}\beta\Phi_{j}.\Phi_{i}\,d\gamma\,\,\mbox{et}\,\,\mathbf{B}_{i}^{cl}=-\int_{\Gamma_{4}}\Phi_{0}N_{i}\,d\gamma\]

Compte tenu de la propriété des fonctions de base, ces contributions interviennent que pour des fonctions de base associées à des noeuds \(M_{i}\) sur la frontière \(\Gamma_{4}\). Le calcul de ces intégrales se décompose en calcul élémentaire sur les arêtes de la frontière \(\Gamma_{4}\). Pour cela nous allons tout d’abord déterminer les arêtes frontières de la géométrie.

Soit AF le tableau des arêtes frontières, i.e. l’ensemble des arêtes des éléments \(e_{k}\) du maillage se trouvant sur la frontière \(\Gamma=\partial\Omega\) de la géométrie:

\[AF=\bigcup_{k=1}^{ne}(e_{k}\cap\Gamma)\]

Chaque arête frontière \(AF_{l}\) est définie par le numéro du premier et du second sommet de l’arête (parcourue dans le sens trigonométrique: i.e. avec une normale extérieure à droite). Le tableau AF est donc un tableau de \(2*naf\) entiers (en notant \(naf\) le nombre total d’arêtes frontières). Par exemple pour la maillage de la figure Fig. 6.14, le nombre d’arêtes frontières vaut \(naf=18\), et le tableau AF vaut:

arêtes AF	numéro 1er sommet	numéro 2nd sommet
[1]	1	2
[2]	6	1
[3]	2	3
\(\vdots\)	\(\vdots\)	\(\vdots\)
[16]	27	26
[17]	29	28
[18]	30	29

Remarque: l’ordre des arêtes est totalement arbitraire.

Pour déterminer ces arêtes, nous utiliserons l’algorithme suivant:

Algorithm 6.2 (Algorithme de détermination des arêtes frontières du maillage)

1. AF1 = [] # liste des arêtes ayant 2 nds frontières

2. pour k de 1 a ne faire # boucle sur les elts

   1. ni = Tbc[k,:] # liste des nds

   2. ni1 = [Tbc[k,1],Tbc[k,2],Tbc[k,3],Tbc[k,1]] # liste des arêtes (permutation)

   3. pour p de 1 a 3 faire # boucle sur les aretes

      1. si Frt[ni1[p]]!=0 et Frt[ni1[p+1]]!=0 alors # mettre dans AF1

         1. AF1.ajout([ni1[p],ni1[p+1]]) # ajoute arête

      2. fin si

   4. fin p

3. fin k

4. na = dimension(AF1)

5. AF = [] # liste des arêtes après élimination des doubles

6. pour p de 1 a na faire # élimination des arêtes doubles

   1. ij = AF1[p] # arête

   2. ji = [ij[2],ij[1]] # et arête symétrique

   3. double = faux # test si arête double

   4. pour q de p+1 a na faire

      1. si AF1[q] == ji alors # arête double

         1. double = vrai

      2. fin si

   5. fin q

   6. si double == faux alors

      1. AF.ajout(ij) # ij est une arête frontière

   7. fin si

7. fin p

Il faut noté qu’une arête frontière n’est pas forcément une arête ayant ses 2 sommets sur la frontière. Ainsi l’élément 33 du maillage de la figure Fig. 6.14 a une arête \([27,21]\) dont les deux sommets sont sur la frontière, mais qui n’est pas frontière. Donc après avoir déterminé la liste des arêtes ayant les 2 sommets sur la frontière (lignes 1 à 3), il faut éliminer les arêtes internes, i.e. apparaissant 2 fois dans la liste. On peut en effet vérifier la propriété suivante:

\[ij\,\mbox{ arete interne}\,\Leftrightarrow\exists k,l\,\mbox{ t.q. }\,ij\in e_{k}\,\mbox{ et }\,ji\in e_{l}\]

Le programme correspondant est donné ci dessous. Pour tester si un noeud est sur une frontière, on utilise le tableau Frt .

import numpy as np

def AreteFrt(G):
    """determine la liste des aretes frontieres"""
    AF = []
    for k in range(G.ne):
        # liste des aretes de l'elt
        ni = np.zeros(4,dtype=int)
        ni[:3] = G.Tbc[k,:]
        ni[3]  = ni[0] 
        for p in range(3):
            if (G.Frt[ni[p]] != 0) and (G.Frt[ni[p+1]] != 0) : 
                AF.append([ni[p],ni[p+1]])
                break
    # elimination des aretes doubles
    na = len(AF)
    ArF = []
    for k in range(na):
        ij = AF[k]
        ji = ij[1::-1]
        if ji not in AF[k+1:]:
            ArF.append(ij)
    #
    return ArF

Ayant la liste AF des arêtes frontières, une intégrale sur \(\Gamma_{4}\) se décompose en intégrale élémentaire:

\[\int_{\Gamma_{4}}f\,d\gamma=\sum_{l=1,\,AF_{l}\in\Gamma_{4}}^{naf}\int_{AF_{l}}f\,d\gamma\]

Pour calculer les intégrales de bord {eq}èq4.24`, il suffit donc de calculer des intégrales élémentaires sur les arêtes frontières de \(\Gamma_{4}\), soit pour une arête \(AF_{l}\) de sommets \(n_{1}=AF(l,1)\) et \(n_{2}=AF(l,2)\) les 6 intégrales suivantes:

\[\mathbf{Af}_{pq}^{l}=\int_{M_{n_{1}}}^{M_{n_{2}}}\beta\Phi_{n_{q}}.\Phi_{n_{p}}\,d\gamma\,\,\mbox{ et }\,\,\mathbf{Bf}_{p}^{l}=-\int_{M_{n_{1}}}^{M_{n_{2}}}\phi_{0}\Phi_{n_{p}}\,d\gamma\,\,\mbox{pour }p,q=1,2\]

puisque sur cette arête, seules 2 fonctions de base sont non nulle: les 2 fonctions de base \(\Phi_{n_{1}}\) et \(\Phi_{n_{2}}\) associées aux 2 sommets. Pour calculer ces intégrales on effectue un changement de variable de l’arête \(AF_{l}\) vers le segment de référence \([-1,1]\) (figure Fig. 6.17).

Fig. 6.17 polynômes \(p_{1},p_{2},p_{3}\) et interpolation \(f^{h}\) sur l’élément 5 (2,6,1)

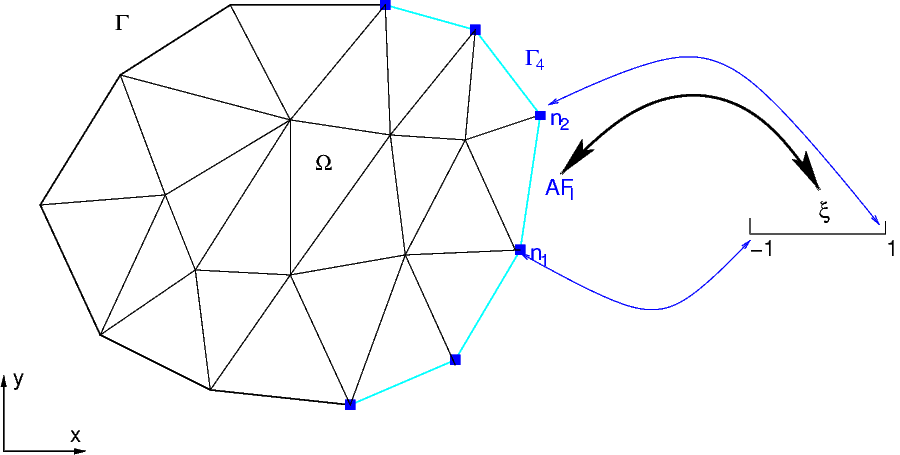
Fig. 6.18 calcul des intégrales frontières

Sur cet élément, l’expression des 2 fonctions de base est très simple: ce sont les 2 polynômes de Lagrange \(\mathcal{P}^{1}\)en \(\xi\)

\[\Phi_{n_{1}}(x,y)\mid_{EF_{l}}=N_{1}(\xi)=\frac{1-\xi}{2}\,\,\mbox{ et }\Phi_{n_{2}}(x,y)\mid_{EF_{l}}=N_{2}(\xi)=\frac{1+\xi}{2}\]

puisque \(\Phi_{n_{1}}\) est une fonction affine qui vaut 1 au noeud \(n_{1}\) et 0 au noeud \(n_{2}\), et idem pour \(\Phi_{n_{2}}\). La variable \(\xi\) a une interprétation géométrique, puisque c’est l’abscisse curviligne sur le segment \([n_{1},n_{2}]\).

Avec ces notations, les intégrales élémentaires de bord s’écrivent:

\[\mathbf{Af}_{pq}^{l}=\int_{-1}^{+1}\beta N_{q}(\xi).N_{p}(\xi)\,\frac{h^{l}}{2}d\xi\,\,\mbox{et}\,\,\mathbf{Bf}_{p}^{l}=-\int_{-1}^{+1}\phi_{0}N_{p}(\xi)\,\frac{h^{l}}{2}d\xi\,\,\mbox{ pour }p,q=1,2 \]

en notant \(h^{l}\) la longueur de l’arête \(AF_{l}\) . Un calcul élémentaire fournit la valeur de ces intégrales dans le cas où \(\beta\) et \(\Phi_{0}\) sont constants par arêtes:

\[\begin{split}\mathbf{Af}^{l}=\beta h^{l}\left[\begin{array}{cc} \frac{1}{3} & \frac{1}{6}\\ \frac{1}{6} & \frac{1}{3} \end{array}\right]\,\mathbf{Bf}^{l}=-\phi_{0}h^{l}\left[\begin{array}{c} \frac{1}{2}\\ \frac{1}{2} \end{array}\right]\end{split}\]

ayant ses 2 sommets sur la frontière. Ayant ces intégrales élémentaires, il suffit ensuite d’appliquer une procédure d’assemblage pour insérer ces contributions dans la matrice \(\mathbf{A}\) et le second membre \(\mathbf{B}\).

Le programme ci dessous implémente cet assemblage. La fonction Climite applique les conditions aux limites en modifiant la matrice et le second membre générique (i.e. calculés sans tenir compte des conditions aux limites). On utilise aussi la convention suivante: les arêtes de la frontière \(\Gamma_{4}\) sont les arêtes ayant au moins un noeud dont le numéro de frontière est égale à 4. Ainsi pour le maillage de la figure Fig. 6.14, la frontière \(\Gamma_{4}\) va du noeud 30 au noeud 26 (et non de 29 à 27). On calcule ainsi toutes les intégrales de bords, mais on modifie aussi l’équation pour les 2 noeuds extrémités 30 et 26. Si ces noeuds sont sur une frontière de Dirichlet (ce qui est le cas), il faudra imposer la condition de Dirichlet après le calcul de ces intégrales de bords. C’est ce qui est fait dans la fonction Climite, où on impose d’abord les conditions faibles, puis ensuite les conditions fortes.

def Climite(G,A,B,beta,phi0,Ue):
   ''' application des CL sur la matrice A et le 2nd mbre B (A et B sont modifiées)'''
   # liste des arêtes frontières
   ArF = AreteFrt(G)
   for ar in ArF:
   	  # test frontiere gamma4 (CL mixte)
   	  if (n1=ar[0]==4) and (n2=ar[1]==4) :
   	    # longueur arête
   	  	dl = np.linalg.norm(G.X[n1,:] - G.X[n2,:])
   	  	A[n1,n1] += beta*dl/3; A[n1,n2] += beta*dl/6;
   	  	A[n2,n1] += beta*dl/6; A[n2,n2] += beta*dl/3;
   	  	B[n1] -= phi0*dl/2
   	  	B[n2] -= phi0*dl/2
   # CL de Dirichlet
   for i in range(G.nn):
   	   if G.Frt[i]==1 :
   	     A[i,:] = 0; A[:,i] = 0; A[i,i] = 1.0
   	     B[i] = 0
   	   elif G.Frt[i] == 2 :
   	     # CL dirichlet non homogene
   	     A[i,:] = 0; A[:,i] = 0; A[i,i] = 1.0
   	     B[i] = Ue
   	#
   	return 

6.2.8. Résolution

Après imposition des conditions aux limites, la solution approchée \(u^{h}\) s’obtient par résolution du système linéaire. Le programme qui enchaîne la suite des opérations pour calculer cette solution approchée est donné ci-dessous.

# résolution du problème modèle
G = Lecture('maillage.msh')
# parametres
alpha=0.; K=1.0; beta=0.0; phi0=-1.0; Ue=2;
# second membre
F = np.zeros(G.nn)
# assemblage
A,B =Assemblage(G,K,alpha,F)
# conditions aux limites
Climite(G,A,B,beta,phi0,Ue)
# resolution
U = np.linalg.solve(A,B)

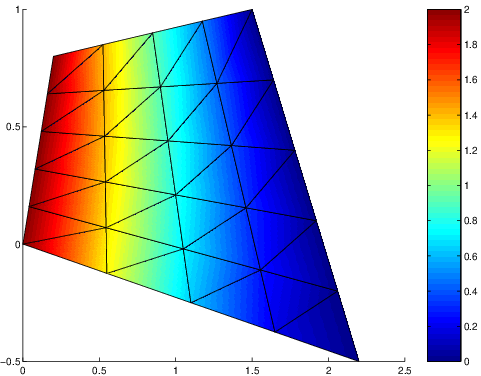
Fig. 6.19 solution \(u^{h}\) pour \(\phi_{0}=0\)

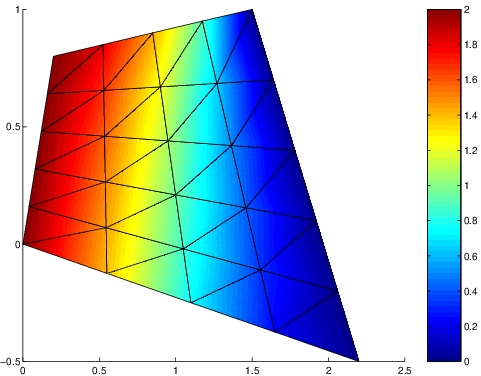
Fig. 6.20 solution \(u^{h}\) pour \(\phi_{0}=-1\)

Pour les valeurs des paramètres du programme ci dessus, on a tracé la solution obtenue pour 2 valeurs de \(\phi_{0}\): \(\phi_{0}=0\) et \(\phi_{0}=-1\) sur les figures Fig. 6.19 et {numref}`fig4.15a}. On constate, sur ce problème simple de diffusion sans terme source, l’influence de la condition aux limites sur \(\Gamma_{4}\) , qui pour le second cas dévie les iso-valeurs de la solution vers la droite par rapport au cas homogène. Ceci correspond bien à l’imposition d’une valeur de dérivée normale positive. On note aussi que les conditions de Neuman ne sont pas vérifiées exactement par la solution approchée, car les iso-valeurs ne sont pas exactement perpendiculaires aux frontières de Neuman. C’est seulement à la limite, que ces conditions seront vérifiées exactement.

6.3. Étude de la précision en éléments finis \(\mathcal{P}^{1}\)

Pour étudier la précision de l’approximation par éléments finis \(\mathcal{P}^{1}\), nous choisissons un cas d’écoulement potentiel où l’on connaît la solution analytique: l’écoulement autour d’un cylindre.

Soit un cylindre de rayon \(a\), placé dans un écoulement uniforme de vitesse \(U_{0}\) suivant x. L’écoulement potentiel autour du cylindre est donnée par la fonction de courant \(\psi_{ex}\) en coordonnées polaires \((r,\theta)\):

\[\psi_{ex}(r,\theta)=U_{0}r\,\sin\theta-U_{0}\frac{a^{2}\sin\theta}{r}\]

qui vérifie l’équation de Laplace:

\[\Delta\Psi=0\label{c4eq25}\]

et la condition aux limites de glissement sur le cylindre:

\[\psi(r=a)=0\]

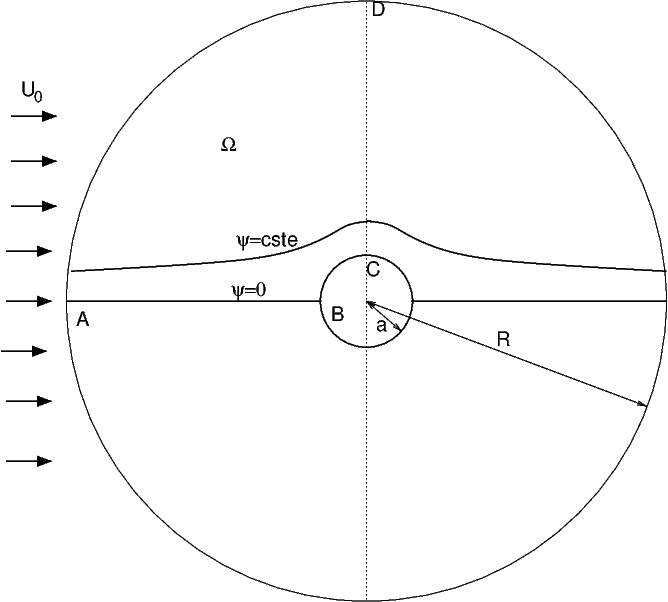
Fig. 6.21 écoulement potentiel autour d’un cylindre

Considérons le domaine \(\Omega\) de la figure Fig. 6.21 de frontière ABCD (soit 1/4 du domaine complet). Sur ce domaine les conditions aux limites sont:

1. en entrée AD \((r=R)\) : $\(\psi_{DA}=U_{0}R\,\sin\theta-U_{0}\frac{a^{2}\sin\theta}{R}\)$

2. sur l’axe AB \((y=0)\), on a une condition de symétrie \((v=0)\), et l’axe AB est la ligne de courant qui arrive sur l’obstacle. La valeur de \(\psi\) vaut donc \(\psi(A)\), soit \(\psi_{AB}=0,\)

3. sur l’obstacle BC \((r=a)\), la valeur de \(\psi\) est constante et égale à celle sur AB, soit \(\psi_{BC}=0\),

4. sur la sortie CD, on impose une condition de symétrie: $\((\frac{\partial\psi}{\partial n})_{CD}=(\frac{\partial\psi}{\partial x})_{x=0}=0.\)$

6.3.1. Maillage \(\mathcal{P}^{1}\)

Pour générer le maillage du domaine \(\Omega\), nous utiliserons les programmes de génération de maillage décrits en annexe. Plus précisément, nous utiliserons la fonction quacou qui maille un domaine à l’aide d’une transformation « quadrilatères courbes » des frontières vers un carré unité que l’on maille (figure Fig. 6.22)

Fig. 6.22 maillage par transformation quacou

On spécifie les points des cotés AB, BC , CD et DA en notant que le nombre de noeuds sur les faces opposées doivent être égaux.

Le maillage obtenu pour \(n_{1}=20\) et \(n_{2}=20\) est tracé sur la figure Fig. 6.23. Ce maillage comprend 400 noeuds et 722 éléments.

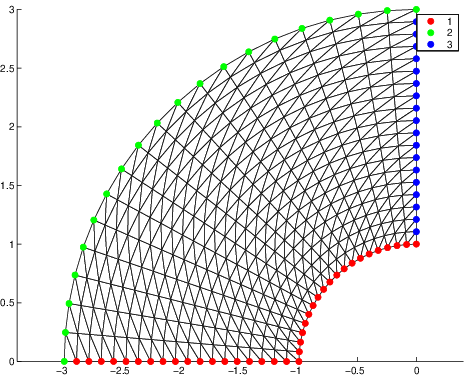
Fig. 6.23 maillage du cylindre

6.3.2. Résolution

En utilisant les programmes précédents, on construit la matrice A et le second membre B du problème discrétisé par éléments finis. Avec l’approche utilisée, la matrice \(A\) est une matrice \((nn,nn)\) qui contient \(160000\) éléments dans le cas du maillage de la figure Fig. 6.23. Or la matrice A a une structure creuse, c’est à dire qu’il y a très peu d’éléments non nuls. Dans notre cas A possède uniquement \(2412\) éléments non nuls, soit moins de \(2\%\).

Exercice: montrer qu’en moyenne pour des éléments \(\mathcal{P}^{1}\), le nombre d’éléments non nuls de A est égale à \(7nn\)

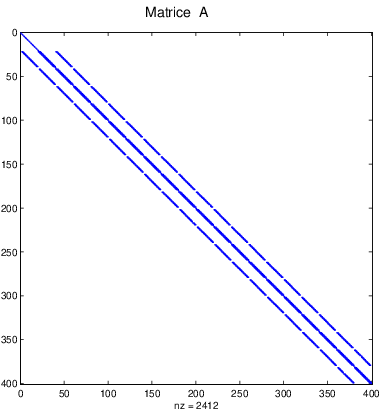
Fig. 6.24 Éléments non nuls de \(\mathbf{A}\)

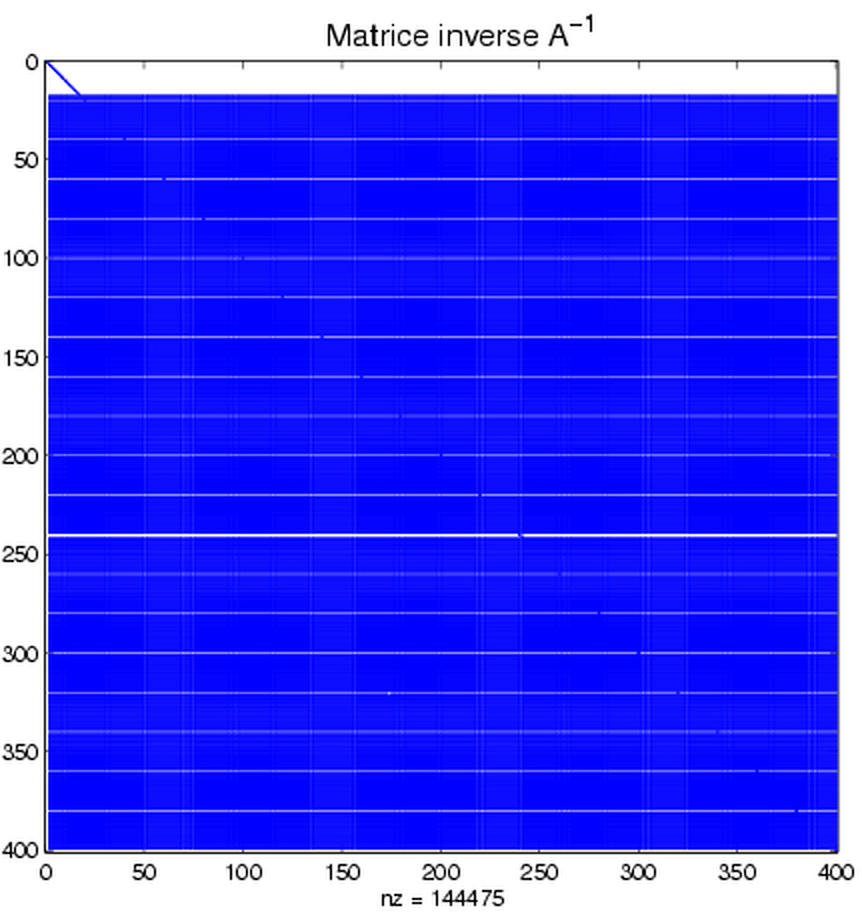
Fig. 6.25 Éléments non nuls de \(\mathbf{A}^{-1}\)

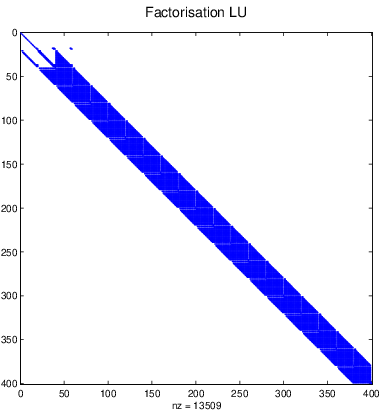
Fig. 6.26 Éléments non nuls de \(\mathbf{L}.\mathbf{U}\)

Au lieu de stocker la matrice A sous la forme d’un tableau à 2 indices, on utilise un stockage creux (sparse en anglais) pour lequel on ne conserve que les éléments non nuls. Pour cela on ne stocke que les valeurs \(A_{i,j}\) et les indices \((i,j)\) des éléments non nuls. Considérons par exemple la matrice creuse \(M\) suivante, qui possède 6 éléments non nuls sur 16:

\[\begin{split}\mathbf{M}=\left[\begin{array}{cccc} 2.0 & 0 & 0 & -1.0\\ 0 & 0 & 4.0 & 0\\ 0 & -3.0 & 1.0 & 0\\ 0 & 0 & 0 & -2.0 \end{array}\right]\end{split}\]

le stockage creux de cette matrice correspond au tableau de 6 lignes et 3 colonnes suivant:

Tableau 6.4 stockage creux d’une matrice \(P^1\)

\(M_{ij}\)	i	j
2.0	1	1
-1.0	1	4
4.0	2	3
-3.0	3	2
1.0	3	3
-2.0	4	4

Dans le cas de la matrice A précédente ce stockage creux est très efficace puisque que l’on utilise un tableau de \(3\times 2412\) éléments au lieu d’un tableau de \(160\,000\) éléments. Par contre si la matrice A est une matrice creuse, son inverse \(\mathbf{A}^{-1}\) est en général une matrice pleine comme le montre la figure Fig. 6.25, où on a marqué par un point bleu les éléments non nuls de A et de \(\mathbf{A}^{-1}\) . Pour la résolution d’un système linéaire linéaire avec une matrice creuse, il faut donc utiliser des méthodes numériques adaptées. Nous avons choisi d’utiliser une factorisation LU de la matrice A qui préserve au maximum le caractère creux de la matrice. Comme le montre la figure Fig. 6.26, cette factorisation génère \(2\times 7\,498\) éléments non nuls au lieu des \(144\,475\) de \(\mathbf{A}^{-1}\) (soit \(10\%\)). Cette factorisation est relativement efficace puisque que la numérotation des noeuds est telle que les éléments non nuls sont proches de la diagonale (voir figure ). Dans le cas d’une numérotation quelconque, il faut appliquer une renumérotation des noeuds de façon à minimiser le remplissage de la matrice lors de la factorisation (par un algorithme de Cuthill-McKee ou un algorithme de degré minimum).

On peut encore améliorer le stockage en tenant compte du caractère symétrique de la matrice A et en ne stockant que la partie triangulaire supérieure de A. Dans ce cas, il faut symétriser la prise en compte des conditions aux limites de Dirichlet: pour un noeud i tel que \(\psi_{i}=\psi^{e}\), il faut modifier la ligne i et la colonne i de A ainsi que le second membre B:

\[\begin{split}\begin{aligned} \mathbf{B}\leftarrow\mathbf{B}-\psi^{e}[A_{i,k}]_{k=1,nn} & B_{1}=\psi^{e}\\ A_{i,k}=A_{k,i}=0 & (k=1,nn)\\ A_{i,i=1}\end{aligned}\end{split}\]

Exercice: modifier les programmes pour prendre en compte cette symétrie.

Pour utiliser un stockage « matrice creuse », nous avons modifier le programme d’assemblage en utilisant une matrice A sparse

Pour cela on fournit une estimation du nombre d’éléments non nuls de A à partir d’un nombre d’arêtes par élément.

Exercice: montrez que le coefficient \(A_{ij}\) est non nul si \(ij\) est une arête du maillage.

Sur chaque élément on a 3 cotés donc 6 arêtes , soit au total une estimation de \(6ne\) arêtes et donc \(6ne+nn\) éléments non nuls. Cette estimation est grossière puisque l’on compte deux fois les arêtes internes. Une estimation exacte nécessiterait de déterminer les arêtes de la géométrie. Dans notre cas le calcul exacte donne \(2242\) arêtes pour une estimation de \(4332,\) soit un nombre d’éléments non nuls estimé de \(4732\) pour \(2642\).

Exercice: écrire l’algorithme et le programme Matlab permettant de déterminer les arêtes de la géométrie.

C’est la seule modification apportée au programme d’assemblage, puisque les calculs des matrices et second membres élémentaires sont inchangés.

Avec ces modifications, la solution approchée \(\psi^{h}\) s’obtiens par résolution du système linéaire par factorisation LU.

Le solution obtenue est tracé sur la figure Fig. 6.27.

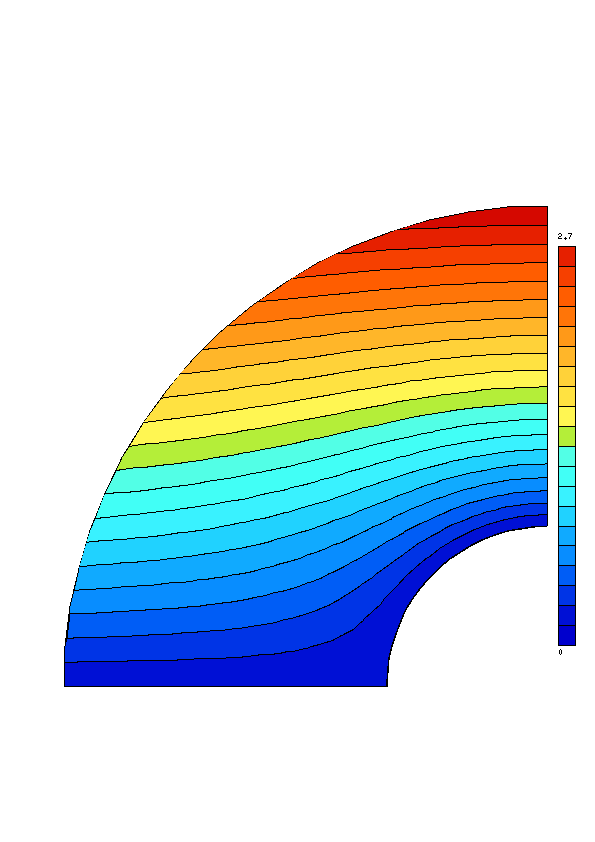
Fig. 6.27 solution \(\psi^{h}\) par éléments finis \(\mathcal{P}^{1}\) avec le maillage

6.3.3. Intégration numérique

Pour déterminer la précision de cette solution numérique \(\psi^{h}\), il faut calculer la norme de l’erreur entre la solution exacte \(\psi_{ex}\) et la solution approchée \(\psi^{h}\):

\[\Vert\psi_{ex}-\psi^{h}\Vert=\sqrt{\int_{\Omega}(\psi_{ex}-\psi^{h})^{2}d\omega}\]

Le calcul de l’intégrale se fait par assemblage, avec un calcul élément par élément:

\[\int_{\Omega}(\psi_{ex}-\psi^{h})^{2}d\omega=\sum_{k=1}^{ne}\int_{e_{k}}(\psi_{ex}-\psi^{h})^{2}d\omega\]

et chaque intégrale élémentaire est calculé par transformation sur l’élément de référence:

\[\int_{e_{k}}(\psi_{ex}-\psi^{h})^{2}d\omega=\det(\mathbf{J}_{k})\,\int_{0}^{1}\int_{0}^{1-\xi}\left(\psi_{ex}(\xi,\eta)-\sum_{p=1}^{3}\psi_{n_{p}}N_{p}(\xi,\eta)\right)^{2}\,d\eta d\xi\label{c4eq30}\]

La fonction \(\psi_{ex}\) n’étant pas polynomiale, on ne sait pas calculer analytiquement cette intégrale. On choisit une intégration numérique par points de Gauss. On approxime l” intégrale d’une fonction \(f(\xi,\eta)\) sur le triangle de référence par une formule de quadrature de Gauss: i.e par une somme pondérée (de poids \(w_{i})\) de valeurs de \(f(\xi,\eta)\) en \(ng\) points de Gauss de coordonnées \((\xi_{i},\eta_{i})\):

\[\int_{0}^{1}\int_{0}^{1-\xi}f(\xi,\eta)\,d\eta d\xi\simeq\,\sum_{i=1}^{ng}w_{i}\,f(\xi_{i},\eta_{i})\]

Les poids \(w_{i}\) et les coordonnées \((\xi_{i},\eta_{i})\) des points de Gauss sont tels que la formule de quadrature soit exacte pour des polynômes de degré le plus élevé possible. Cette formule possède \(3ng\) degrés de liberté, on peux donc imposer \(3ng\) contraintes. Ainsi pour intégrer exactement des polynômes de degré 1 en \((\xi,\eta)\) (ce qui impose 3 conditions) , il suffit d’un seul point de Gauss, l’intersection des médianes:

\[\int_{0}^{1}\int_{0}^{1-\xi}f(\xi,\eta)\,d\eta d\xi\simeq\frac{1}{2}f(\frac{1}{3},\frac{1}{3})\]

Exercice: démontrer cette formule de quadrature.

Pour un triangle, les points de Gauss doivent vérifier des propriétés de symétrie: i.e. leurs coordonnées barycentriques sont obtenues par permutations circulaires et les poids sont équivalents. Les points de Gauss sont donc à une même distance sur les médianes du triangle.

Ainsi la formule de quadrature utilisant 3 points de Gauss sur les médianes s’écrit:

\[\int_{0}^{1}\int_{0}^{1-\xi}f(\xi,\eta)\,d\eta d\xi\simeq w_{1}f(\xi_{1},\xi_{1})+w_{1}f(1-2\xi_{1},\xi_{1})+w_{1}f(\xi_{1},1-2\xi_{1})\]

En écrivant que cette formule doit être exacte pour les polynômes de degré \(\le2\), i.e. pour \(f=1,\,\xi,\,\eta,\,\xi\eta,\,\xi^{2},\,\eta^{2}\), on en déduit les relations (non linéaires) que doivent vérifier \(w_{1}\) et \(\xi_{1}\).Parmi ces relations, deux sont indépendantes, ce qui permet de déterminer \(w_{1}\) et \(\xi_{1}\).

Dans ce cas on trouve 2 solutions:

\[w_{1}=\frac{1}{6},\,\xi_{1}=\frac{1}{2}\,\mbox{ ou }w_{1}=\frac{1}{6},\,\xi_{1}=\frac{1}{6}\]

qui permette d’intégrer exactement des polynômes de degré \(\le2\). La seconde solution est la plus précise, puisque l’erreur d’intégration pour des polynômes de degré 3 est la plus faible.

Avec cette approche, on peut déterminer les points de Gauss pour des intégrations exactes de polynômes. Dans le tableau suivant sont donnés les formules de quadrature de Gauss précises de l’ordre 1 à 5. Les paramètres exactes de ces formules de Gauss, obtenus en suivant la même démarche que précédemment, sont donnés dans le tableau, ainsi que leurs valeurs numériques approchées[3].

Tableau 6.5 points de Gauss pour l’intégration numérique sur un triangle

ordre	formule	figure	poids	\(\xi_{i}\)	\(\eta_{i}\)
1	\(w_{1}f(\xi_{1},\eta_{1})\)		\(w_{1}=p\)	\(\xi_{1}=\lambda\)	\(\eta_{1}=\lambda\)1
2	\(w_{1}f(\xi_{1},\eta_{1})\)		\(w_{1}=p\)	\(\xi_{1}=\lambda\)	\(\eta_{1}=\lambda\)
	\(+w_{2}f(\xi_{2},\eta_{2})\)		\(w_{2}=p\)	\(\xi_{2}=1-2\lambda\)	\(\eta_{2}=\lambda\)
	\(+w_{3}f(\xi_{3},\eta_{3})\)		\(w_{3}=p\)	\(\xi_{3}=\lambda\)	\(\eta_{3}=1-2\lambda\)
3	\(w_{1}f(\xi_{1},\eta_{1})\)		\(w_{1}=p_{1}\)	\(\xi_{1}=\lambda_{1}\)	\(\eta_{1}=\lambda_{1}\)
	\(+w_{2}f(\xi_{2},\eta_{2})\)		\(w_{2}=p_{1}\)	\(\xi_{2}=1-2\lambda_{1}\)	\(\eta_{2}=\lambda_{1}\)
	\(+w_{3}f(\xi_{3},\eta_{3})\)		\(w_{3}=p_{1}\)	\(\xi_{3}=\lambda_{1}\)	\(\eta_{3}=1-2\lambda_{1}\)
	\(+w_{4}f(\xi_{4},\eta_{4})\)		\(w_{4}=p_{2}\)	\(\xi_{4}=\lambda_{2}\)	\(\eta_{4}=\lambda_{2}\)
4	\(w_{1}f(\xi_{1},\eta_{1})\)		\(w_{1}=p_{1}\)	\(\xi_{1}=\lambda_{1}\)	\(\eta_{1}=\lambda_{1}\)
	\(+w_{2}f(\xi_{2},\eta_{2})\)		\(w_{2}=p_{1}\)	\(\xi_{2}=1-2\lambda_{1}\)	\(\eta_{2}=\lambda_{1}\)
	\(+w_{3}f(\xi_{3},\eta_{3})\)		\(w_{3}=p_{1}\)	\(\xi_{3}=\lambda_{1}\)	\(\eta_{3}=1-2\lambda_{1}\)
	\(+w_{4}f(\xi_{4},\eta_{5})\)		\(w_{4}=p_{2}\)	\(\xi_{4}=\lambda_{2}\)	\(\eta_{4}=\lambda_{2}\)
	\(+w_{5}f(\xi_{5},\eta_{5})\)		\(w_{5}=p_{2}\)	\(\xi_{5}=1-2\lambda_{2}\)	\(\eta_{5}=\lambda_{2}\)
	\(+w_{6}f(\xi_{6},\eta_{6})\)		\(w_{6}=p_{2}\)	\(\xi_{6}=\lambda_{2}\)	\(\eta_{6}=1-2\lambda_{2}\)
5	\(w_{1}f(\xi_{1},\eta_{1})\)		\(w_{1}=p_{1}\)	\(\xi_{1}=\lambda_{1}\)	\(\eta_{1}=\lambda_{1}\)
	\(+w_{2}f(\xi_{2},\eta_{2})\)		\(w_{2}=p_{1}\)	\(\xi_{2}=1-2\lambda_{1}\)	\(\eta_{2}=\lambda_{1}\)
	\(+w_{3}f(\xi_{3},\eta_{3})\)		\(w_{3}=p_{1}\)	\(\xi_{3}=\lambda_{1}\)	\(\eta_{3}=1-2\lambda_{1}\)
	\(+w_{4}f(\xi_{4},\eta_{4})\)		\(w_{4}=p_{2}\)	\(\xi_{4}=\lambda_{2}\)	\(\eta_{4}=\lambda_{2}\)
	\(+w_{5}f(\xi_{5},\eta_{5})\)		\(w_{5}=p_{3}\)	\(\xi_{5}=\lambda_{3}\)	\(\eta_{5}=\lambda_{3}\)
	\(+w_{6}f(\xi_{6},\eta_{6})\)		\(w_{6}=p_{3}\)	\(\xi_{6}=1-2\lambda_{3}\)	\(\eta_{6}=\lambda_{3}\)
	\(+w_{7}f(\xi_{7},\eta_{7})\)		\(w_{7}=p_{3}\)	\(\xi_{7}=\lambda_{3}\)	\(\eta_{7}=1-2\lambda_{3}\)

On constate que pour l’ordre 3 (i.e. avec 4 points de Gauss), le poids \(p_{2}\) associé au noeud central est négatif. La formule de quadrature ne préserve donc pas la positivité de l’intégrale lorsque l’intégrante \(f(\xi,\eta)\) est positif: i.e.

\[f(\xi,\eta)\ge0\Longrightarrow\int_{0}^{1}\int_{0}^{1-\xi}f(\xi\,\eta)\,d\eta d\xi>0\]

Cette formule n’est donc pas utilisable en pratique et seul les ordres 2,4 ou 5 sont utilisés.

Tableau 6.6 paramètres pour l’intégration numérique sur un triangle

ordre	paramètres	valeur approchée
1	\(p=\frac{1}{6} \,,\,\lambda=\frac{1}{3}\)
2	\(p=\frac{1}{6},\,\lambda=\frac{1}{6}\)
3	\(p_{1}=\frac{25}{96},\,\lambda_{1}=\frac{1}{5}\)	\(p_{1}\approx0.2604166667\)
	\(p_{2}=-\frac{9}{32},\,\lambda_{2}=\frac{1}{3}\)	\(p_{2}=-0.281250\)
4	\(p_{1}=\frac{1}{12}+(\frac{1}{7440}-\frac{3\sqrt{10}}{4960})\sqrt{950-220\sqrt{10}}\)	\(\approx0.05497587183\)
	\(\lambda_{1}=\frac{4}{9}-\frac{\sqrt{10}}{18}-\frac{\sqrt{950-220\sqrt{10}}}{90}\)	\(\approx0.0915762136\)
	\(p_{2}=\frac{1}{12}-(\frac{1}{7440}-\frac{3\sqrt{10}}{4960})\sqrt{950-220\sqrt{10}}\)	\(\approx0.1116907948\)
	\(\lambda_{2}=\frac{4}{9}-\frac{\sqrt{10}}{18}+\frac{\sqrt{950-220\sqrt{10}}}{90}\)	\(\approx0.4459484908\)
5	\(p_{1}=\frac{31}{480}-\frac{\sqrt{15}}{2400}\)	\(\approx0.06296959026\)
	\(\lambda_{1}=\frac{2}{7}-\frac{\sqrt{15}}{21}\)	\(\approx0.1012865073\)
	\(p_{2}=\frac{9}{80},\,\lambda_{2}=\frac{1}{3}\)	\(p_{2}=0.11250\)
	\(p_{3}=\frac{31}{480}+\frac{\sqrt{15}}{2400}\)	\(\approx0.06619707639\)
	\(\lambda_{3}=\frac{2}{7}+\frac{\sqrt{15}}{21}\)	\(\approx0.4701420641\)

Pour terminer sur l’intégration sur le triangle de référence, nous donnons les formules d’intégration exacte pour les polynômes. Un calcul directe montre que pour tous les entiers positifs n et m on a :

\[\int_{0}^{1}\int_{0}^{1-\xi}\xi^{m}\eta^{n}\,d\eta d\xi=\frac{m!n!}{(n+m+2)!}\]

d’où l’on déduit la formule d’intégration pour les fonctions de forme:

\[\int_{0}^{1}\int_{0}^{1-\xi}N_{1}^{l}N_{2}^{m}N_{3}^{n}\,d\eta d\xi=\frac{l!m!n!}{(l+n+m+2)!}\]

Exercice: démontrer cette formule.

Pour calculer l’intégrale élémentaire dans l’expression de l’erreur, nous avons utilisé une intégration numérique d’ordre 2 avec 3 points de Gauss.

6.3.4. Détermination de la précision

La précision d’une solution par éléments finis dépend du degré de l’élément et de la taille \(h\) des éléments. Pour un triangle \(e_{k}\), on définit la taille \(h_{k}\) comme la longueur du plus grand coté (figure Fig. 6.28). On définit aussi le diamètre \(d_{i}\) du cercle inscrit et le diamètre \(d_{e}\) du cercle circonscrit, ainsi que le rapport d’aspect du triangle \(R=\frac{d_{i}}{d_{e}}\). Pour un triangle équilatéral, on a \(d_{e}=h\) et \(d_{i}=\frac{\sqrt{2}}{3}h\), donc \(R=\frac{\sqrt{2}}{3}\). Par contre pour un triangle de plus en plus aplati, le rapport d’aspect tend vers 0 (car \(d_{i}\rightarrow0\)) , ce qui indique la dégénérescence du triangle.

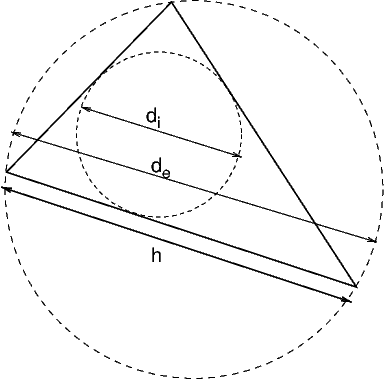
Fig. 6.28 longueurs caractéristiques d’un triangle

Avec ces définitions, on montre que l’erreur d’interpolation \(\mathcal{P}^{1}\) sur un triangle vérifie une relation analogue au cas 1D:

\[\left\Vert f-f^{h}\right\Vert =\sqrt{\int_{e_{k}}(f-f^{h})^{2}\,dxdy}\,\le\,C\,h_{k}^{2}\,\sqrt{\int_{e_{k}}\left((\frac{\partial^{2}f}{\partial x^{2}})^{2}+(\frac{\partial^{2}f}{\partial y^{2}})^{2}\right)dxdy}\]

Cependant la constante \(C\) dépend du rapport d’aspect \(R\) et l’estimation d’erreur dégénère lorsque \(R\rightarrow0\), i.e. lorsque le triangle devient de plus en plus aplatis.

L’erreur d’approximation étant borné par l’erreur d’interpolation, on déduit une estimation de l’erreur d’approximation \(\left\Vert \psi_{ex}-\psi^{h}\right\Vert\) sur un maillage non dégénéré de taille caractéristique \(h\):

\[\left\Vert \psi_{ex}-\psi^{h}\right\Vert =\sqrt{\int_{\Omega}(\psi_{ex}-\psi^{h})^{2}\,d\omega}\,\le\,C\,h^{2}\,\sqrt{\int_{\Omega}\left((\frac{\partial^{2}f}{\partial x^{2}})^{2}+(\frac{\partial^{2}f}{\partial y^{2}})^{2}\right)d\omega}\]

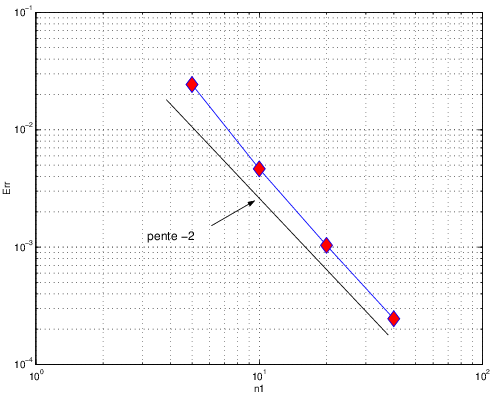
Fig. 6.29 Norme de l’erreur d’approximation \(\mathcal{P}^{1}\) en fonction de \(n\propto h^{-1}\)

Nous avons donc construit une série de maillage de \(\Omega,\) avec une taille \(h\rightarrow0\) et un rapport d’aspect \(R\) constant en fixant un nombre de noeuds identiques sur les cotés lors de la génération du maillage: i.e. \(n_{1}=n_{2}=n\). Dans ce cas la taille des éléments \(h\) est proportionnelle à \(\frac{1}{n}\). On a donc tracé sur la figure Fig. 6.29, la norme de l’erreur en fonction de \(n\) et on vérifie que l’on obtiens une décroissance de l’erreur en \(n^{-2}\), soit en \(\theta(h^{2})\), ce qui montre que l’approximation par éléments finis \(\mathcal{P}^{1}\) est d’ordre 2.

6.4. Éléments finis quadrangulaire \(\mathcal{Q}^{1}\)

La seconde façon de mailler un domaine \(\Omega\) est d’utiliser des quadrangles. Bien qu’ayant des possibilités de maillage moins générale que les triangles, les maillages quadrangulaires sont cependant très utilisés, en particulier en mécanique des solides, car ils peuvent être plus précis. L’autre intérêt des approximations quadrangulaires est que ce sont des produits tensoriels d’approximation 1D.

Le maillage quadrangulaire est décrit par une structure de données G identique à celle du maillage triangulaire, mais avec un nombre de degré de liberté par élément G.ddl=4 et une table de connection G.Tbc à 4 éléments ( de dimension 4*ne). Un exemple de maillage du cylindre est donné sur la figure {numref}`fig4.23a}.

Fig. 6.30 Maillage \(\mathcal{Q}^{1}\) du cylindre

L’élément \(\mathcal{Q}^{1}\) est l’élément quadrangulaire le plus simple, qui possède comme degrés de liberté les valeurs aux 4 sommets du quadrangle.

6.4.1. Élément de référence et fonctions de forme

L’approximation sur un élément \(\mathcal{Q}^{1}\) est définie à l’aide d’une transformation vers un élément de référence, qui est le carré \([-1,+1]*[-1,+1]\).

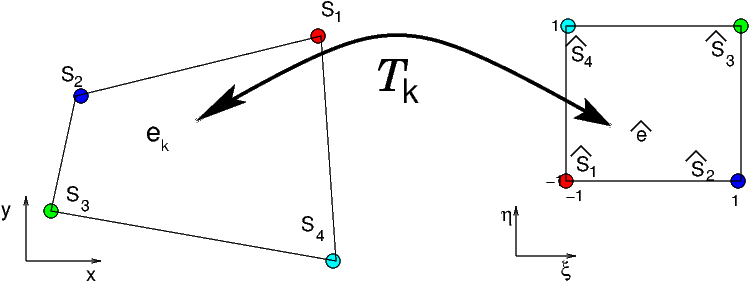
Fig. 6.31 transformation \(\mathcal{T}_{k}:\,(x,y)\Leftrightarrow(\xi,\eta)\) vers l’élément de référence \(\mathcal{Q}^{1}\) écoulement potentiel dans un canal

Cette transformation \(\mathcal{T}^{k}\) est une transformation bilinéaire, qui transforme les 4 sommets \(\{S_{q}\}_{q=1,4}\) de \(e_{k}\) vers les 4 sommets \(\{\hat{S}_{q}\}_{q=1,4}\) de l’élément de référence \(\hat{e}\).

Sur cet élément de référence, l’approximation \(f^{h}\) d’une fonction \(f\) est une fonction bilinéaire (i.e. le produit d’un polynôme de degré 1 en \(\xi\) par un polynôme de degré 1 en \(\eta\)):

\[f_{|e_{k}}^{h}(\xi,\eta)=a\xi\eta+b\xi+c\eta+d\]

Les coefficients \(\{a,b,c,d\}\) dépendent linéairement des valeurs \(\{F_{n_{q}}\}_{q=1,4}\) de \(f^{h}\) aux 4 sommets de l’élément (on a noté \(\{n_{q}\}_{q=1,4}\) les numéros des 4 sommets). Cette approximation s’écrit donc sous la forme:

\[f_{|e_{k}}^{h}(\xi,\eta)=F_{n_{1}}N_{1}(\xi,\eta)+F_{n_{2}}N_{2}(\xi,\eta)+F_{n_{3}}N_{3}(\xi,\eta)+F_{n_{4}}N_{4}(\xi,\eta)\]

Les fonctions \(\{N_{q}(\xi,\eta)\}_{q=1,4}\) sont les fonctions de forme de l’élément \(\mathcal{Q}^{1}\): ce sont des fonctions bilinéaires qui vérifient:

\[N_{q}(\hat{S}_{p})=\delta_{p,q}\,\mbox{\, \, pour\, }\,p,q=1,4\]

Ce sont les polynômes de Lagrange de degré 1, dont l’expression est la suivante:

\[\begin{split}\begin{aligned} N_{1}(\xi,\eta)=\frac{1}{4}(1-\xi)(1-\eta)\\ N_{2}(\xi,\eta)=\frac{1}{4}(1+\xi)(1-\eta)\\ N_{3}(\xi,\eta)=\frac{1}{4}(1+\xi)(1+\eta)\\ N_{4}(\xi,\eta)=\frac{1}{4}(1-\xi)(1+\eta)\end{aligned}\end{split}\]

Ces fonctions de forme \(\mathcal{Q}^{1}\) sont tracées sur la figure Fig. 6.32. Ce sont des surfaces réglées et non plus des plans comme pour les fonctions de forme \(\mathcal{P}^{1}\).

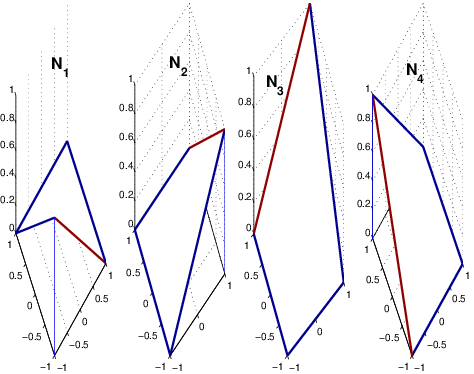
Fig. 6.32 fonctions de forme \(\mathcal{Q}^{1}\)

Ces fonctions de formes vont nous permettre aussi de déterminer la transformation \(\mathcal{T}^{k}\) puisque les coordonnées d’un point \((x,y)\) de l’élément \(e_{k}\) dépend linéairement des coordonnées \(\{x_{n_{q}},y_{n_{q}}\}\) des sommets \(\{S_{q}\}\) de l’élément et est une fonction bilinéaire de \((\xi,\eta)\)

\[\begin{split}\begin{aligned} x=x_{n_{1}}N_{1}(\xi,\eta)+x_{n_{2}}N_{2}(\xi,\eta)+x_{n_{3}}N_{3}(\xi,\eta)+x_{n_{4}}N_{4}(\xi,\eta)\\ y=y_{n_{1}}N_{1}(\xi,\eta)+y_{n_{2}}N_{2}(\xi,\eta)+y_{n_{3}}N_{3}(\xi,\eta)+y_{n_{4}}N_{4}(\xi,\eta)\nonumber \end{aligned}\end{split}\]

La matrice jacobienne \(\mathbf{J}_{k}\)= \(\frac{D(x,y)}{D(\xi,\eta)}\) de cette transformation se calcule alors simplement:

\[\begin{split}\mathbf{J}_{k}=\frac{1}{4}\left[\begin{array}{cc} (x_{n_{2}}-x_{n_{1}})(1-\eta)+(x_{n_{3}}-x_{n_{4}})(1+\eta) & (x_{n_{4}}-x_{n_{1}})(1-\xi)+(x_{n_{3}}-x_{n_{2}})(1+\xi)\\ (y_{n_{2}}-y_{n_{1}})(1-\eta)+(y_{n_{3}}-y_{n_{4}})(1+\eta) & (y_{n_{4}}-y_{n_{1}})(1-\xi)+(y_{n_{3}}-y_{n_{2}})(1+\xi) \end{array}\right]\end{split}\]

On constate que contrairement à l’élément \(\mathcal{P}^{1}\), la matrice jacobienne de cette transformation n’est pas constante. Dans le cas d’un quadrangle rectangle de cotés \(h_{1}\) et \(h_{2}\) alignés avec les axes, cette matrice jacobienne \(\mathbf{J}_{k}\) se simplifie:

\[\begin{split}\mathbf{J}_{k}=\frac{1}{2}\left[\begin{array}{cc} h_{1} & 0\\ 0 & h_{2} \end{array}\right]\end{split}\]

Exercice: montrer que si les cotés du quadrangles sont parallèles, alors la matrice jacobienne est constante. Calculer \(\mathbf{J}_{k}\) dans ce cas.

6.4.2. Intégration numérique

La transformation vers l’élément de référence est pour un quadrangle quelconque plus complexe que pour les éléments \(\mathcal{P}^{1}\). Le calcul des intégrales sur l’élément de référence, qui fait intervenir le déterminant du Jacobien, voir la jacobienne inverse, ne se fait plus en générale analytiquement, mais utilise une intégration numérique.

L’intégration numérique sur l’élément de référence \(\mathcal{Q}^{1}\) est cependant plus simple que l’intégration numérique sur un élément \(\mathcal{P}^{1}\), puisque les bornes d’intégration en \((\xi,\eta)\) sont fixes. Cette intégration est en faite un produit tensoriel d’intégrations numériques en 1D.

6.4.2.1. intégration numérique 1D

Sur le segment de référence \([-1,+1]\), l’intégration numérique d’une fonction \(f(\xi)\) utilisant \(ng\) points de Gauss s’écrit:

\[\int_{-1}^{+1}f(\xi)\,d\xi\simeq\,\sum_{i=1}^{ng}w_{i}\,f(\xi_{i})\]

Les paramètres de cette formule de quadrature sont tels que l’intégration soit exacte pour les polynômes de degré le plus élevé possible. Cette formule ayant \(2ng\) paramètres \(\{w_{i},\xi_{i}\}\), on va pouvoir imposer \(2ng\) conditions: i.e intégrer exactement tous les monômes \(\xi^{m}\) pour \(m=0,2ng-1\). La formule d’intégration avec \(ng\) points de Gauss va permettre d’intégrer exactement tous les polynômes de degré \(\le2ng-1\).

Par exemple avec 2 points de Gauss on peut intégré exactement des polynômes de degré \(\le3\). Cette formule s’écrit:

(6.35)\[\int_{-1}^{+1}f(\xi)\,d\xi\simeq\,w_{1}\,f(\xi_{1})+w_{2}\,f(\xi_{2})\]

En écrivant que cette formule (6.35) est exacte pour \(f=1,\xi,\xi^{2},\xi^{3}\) on obtiens les 4 relations permettant de déterminer les 4 coefficients \(\{w_{1},\xi_{1},w_{2},\xi_{2}\}\). On peut aussi noter que cette formule doit être symétrique, et donc que l’on a forcément: \(\xi_{1}=-\xi_{2}\) et \(w_{1}=w_{2}\). La condition pour \(f=1\) donne immédiatement la valeur \(w_{1}=1\), et la condition pour \(f=\xi^{2}\) la valeur \(\xi_{1}=\frac{\sqrt{3}}{3}\). D’où la formule de quadrature à 2 points:

\[\int_{-1}^{+1}f(\xi)\,d\xi\simeq\,f(-\frac{\sqrt{3}}{3})+f(\frac{\sqrt{3}}{3})\]

Les positions \(\xi_{i}\) des points de Gauss sont les racines de polynômes caractéristiques: les polynômes de Legendre.On a cependant pas d’expressions analytiques générales pour ces racines, et il faut les déterminer pour chaque valeur de \(ng\).

A l’aide d’un outil de calcul formel, on détermine analytiquement ces valeurs jusqu’à \(ng=5\) en utilisant les propriétés de symétrie de ces points de Gauss.

Exercice: en s’inspirant du programme précédent, déterminer la formule de quadrature de Gauss pour \(ng=4.\)

Le tableau ci-dessous donne les expressions analytiques, ainsi que les valeurs numériques approchées (que l’on comparera avec les valeurs numériques données classiquement dans les livres), pour les formules de quadrature de Gauss d’ordre 1 à 9 (i.e. pour \(ng=1,5\)).

Tableau 6.7 Intégration numérique 1D

ordre	formule	poids	position	paramètres	valeurs
1	\(w_{1}f(\xi_{1})\)	\(w_{1}=2\)	\(\xi_{1}=0\)
3	\(w_{1}f(\xi_{1})\)	\(w_{1}=p_{1}\)	\(\xi_{1}=+\lambda_{1}\)	\(p_{1}=\)1
	\(+w_{2}f(\xi_{2})\)	\(w_{2}=p_{1}\)	\(\xi_{2}=-\lambda_{1}\)	\(\lambda_{1}=\frac{\sqrt{3}}{3}\)	\(\approx0.5773502693\)
5	\(w_{1}f(\xi_{1})\)	\(w_{1}=p_{1}\)	\(\xi_{1}=+\lambda_{1}\)	\(p_{1}=\frac{5}{9}\)	\(\approx0.5555555556\)
	\(+w_{2}f(\xi_{2})\)	\(w_{2}=p_{1}\)	\(\xi_{2}=-\lambda_{1}\)	\(\lambda_{1}=\frac{\sqrt{15}}{5}\)	\(\approx0.7745966692\)
	\(+w_{3}f(\xi_{3})\)	\(w_{3}=p_{2}\)	\(\xi_{3}=0\)	\(p_{2}=\frac{8}{9}\)	\(\approx0.8888888889\)
7	\(w_{1}f(\xi_{1})\)	\(w_{1}=p_{1}\)	\(\xi_{1}=+\lambda_{1}\)	\(p_{1}=\frac{1}{2}+\frac{\sqrt{30}}{36}\)	\(\approx0.6521451549\)
	\(+w_{2}f(\xi_{2})\)	\(w_{2}=p_{1}\)	\(\xi_{2}=-\lambda_{1}\)	\(\lambda_{1}=\frac{\sqrt{525-70\sqrt{30}}}{35}\)	\(\approx0.3399810437\)
	\(+w_{3}f(\xi_{3})\)	\(w_{3}=p_{2}\)	\(\xi_{3}=+\lambda_{2}\)	\(p_{2}=\frac{1}{2}-\frac{\sqrt{30}}{36}\)	\(\approx0.3478548451\)
	\(+w_{4}f(\xi_{4})\)	\(w_{4}=p_{1}\)	\(\xi_{4}=-\lambda_{2}\)	\(\lambda_{2}=\frac{\sqrt{525+70\sqrt{30}}}{35}\)	\(\approx0.8611363114\)
9	\(\,w_{1}f(\xi_{1})\)	\(w_{1}=p_{1}\)	\(\xi_{1}=+\lambda_{1}\)	\(p_{1}=\frac{322+13\sqrt{70}}{900}\)	\(\approx0.4786286705\)
	\(+w_{2}f(\xi_{2})\)	\(w_{2}=p_{1}\)	\(\xi_{2}=-\lambda_{1}\)	\(\lambda_{1}=\frac{\sqrt{245-14\sqrt{70}}}{21}\)	\(\approx0.5384693100\)
	\(+w_{3}f(\xi_{3})\)	\(w_{3}=p_{2}\)	\(\xi_{3}=+\lambda_{2}\)	\(p_{2}=\frac{322-13\sqrt{70}}{900}\)	\(\approx0.2369268851\)
	\(+w_{4}f(\xi_{4})\)	\(w_{4}=p_{1}\)	\(\xi_{4}=-\lambda_{2}\)	\(\lambda_{2}=\frac{\sqrt{245+14\sqrt{70}}}{21}\)	\(\approx0.9061798457\)
	\(+w_{5}f(\xi_{5})\)	\(w_{5}=p_{3}\)	\(\xi_{3}=0\)	\(p_{3}=\frac{128}{225}\)	\(\approx0.5688888889\)

6.4.2.2. intégration numérique en 2D

Ayant les formules de quadrature de Gauss en 1D, on en déduit les formules de quadrature en 2D en intégrant successivement suivant \(\xi\) et \(\eta\):

(6.36)\[\begin{split}\begin{aligned} \int_{-1}^{+1}\int_{-1}^{+1}f(\xi,\eta)\,d\xi d\eta & \approx & \sum_{i=1}^{ng}w_{i}\int_{-1}^{+1}f(\xi_{i},\eta)\,d\eta \\ & \approx & \sum_{i=1}^{ng}w_{i}\sum_{j=1}^{ng}w_{j}f(\xi_{i},\eta_{j})\\ & \approx & \sum_{i=1}^{ng}\sum_{j=1}^{ng}w_{i}w_{j}f(\xi_{i},\eta_{j})\end{aligned}\end{split}\]

Cette formule de quadrature (6.36) est bien le produit tensoriel de formule 1D.

Remarque: on peut évidement choisir un nombre de points de Gauss différent suivant chaque direction.

6.4.3. Matrices élémentaires

Par rapport à la formulation élément finis \(\mathcal{P}^{1}\), le seul changement provient du calcul des matrices élémentaires, puisque l’assemblage et le calcul des intégrales de bords restent identiques.

6.4.3.1. matrice élémentaire de rigidité

L’expression de la matrice élémentaire de rigidité \(\mathbf{K}^{k}\) s’écrit:

\[\begin{split}\mathbf{K}_{pq}^{k}=\int_{-1}^{+1}\int_{-1}^{+1}\left(\left[\begin{array}{cc} \frac{\partial N_{p}}{\partial\xi} & \frac{\partial N_{p}}{\partial\eta}\end{array}\right](\mathbf{J}_{k}^{-1})\right).\left((\mathbf{J}_{k}^{-1})^{t}\left[\begin{array}{c} \frac{\partial N_{q}}{\partial\xi}\\ \frac{\partial N_{q}}{\partial\eta} \end{array}\right]\right)\det(\mathbf{J}_{k})\,d\eta d\xi\,\,\,p,q=1,4\end{split}\]

Pour calculer ces intégrales, nous utiliserons une intégration numérique avec 2 points de Gauss dans chaque direction.

Remarque: on peut vérifier numériquement que la précision d’intégration est suffisante, puisque que pour des quadrangles pas trop déformés, on obtiens la solution exacte.

Dans le cas d’un triangle rectangle de cotés \(h_{1}\) et \(h_{2}\) alignés suivant les axes \(x\) et \(y\), la matrice jacobienne est constante et on peut calculer analytiquement la matrice de rigidité:

\[\begin{split}\mathbf{K}^{k}=\frac{1}{6h_{1}h_{2}}\left[\begin{array}{cccc} 2(h_{1}^{2}+h_{2}^{2}) & h_{1}^{2}-2h_{2}^{2} & -(h_{1}^{2}+h_{2}^{2}) & h_{2}^{2}-2h_{1}^{2}\\ h_{1}^{2}-2h_{2}^{2} & 2(h_{1}^{2}+h_{2}^{2}) & h_{2}^{2}-2h_{1}^{2} & -(h_{1}^{2}+h_{2}^{2})\\ -(h_{1}^{2}+h_{2}^{2}) & h_{2}^{2}-2h_{1}^{2} & 2(h_{1}^{2}+h_{2}^{2}) & h_{1}^{2}-2h_{2}^{2}\\ h_{2}^{2}-2h_{1}^{2} & -(h_{1}^{2}+h_{2}^{2}) & h_{1}^{2}-2h_{2}^{2} & 2(h_{1}^{2}+h_{2}^{2}) \end{array}\right]\end{split}\]

On vérifie que la matrice est symétrique et que la somme des lignes et des colonnes est nulle.

Exercice: démontrer la relation précédente pour \(\mathbf{K}^{k}\)

6.4.3.2. matrice élémentaire de masse

L’expression de la matrice élémentaire de masse \(\mathbf{M}^{k}\) s’écrit:

\[\mathbf{M}_{pq}^{k}=\int_{-1}^{+1}\int_{-1}^{+1}N_{q}(\xi,\eta)N_{p}(\xi,\eta)\det(\mathbf{J}_{k})\,d\eta d\xi\,\,\,p,q=1,4\]

Pour calculer ces intégrales nous utiliserons une intégration numérique de Gauss avec 2 points de Gauss dans chaque direction, bien que l’on puisse les calculer analytiquement. En effet le déterminant du Jacobien \(\det(\mathbf{J}_{k})\) est un polynôme de degré 1 en \(\xi\) et \(\eta,\) et donc \(\mathbf{M}_{pq}^{k}\) est une intégrale de polynômes de degré 3 en \(\xi\) et \(\eta\). Mais l’expression obtenue reste cependant complexe et n’est pas généralisable au cas où le coefficient \(\alpha\) devant la matrice de masse est variable.

Dans le cas d’un triangle rectangle de cotés \(h_{1}\) et \(h_{2}\) alignés suivant les axes \(x\) et \(y\), le Jacobien de la transformation est constant et on peut calculer simplement la matrice de masse:

\[\begin{split}\mathbf{M}_{pq}^{k}=\frac{h_{1}h_{2}}{36}\left[\begin{array}{cccc} 4 & 2 & 1 & 2\\ 2 & 4 & 2 & 1\\ 1 & 2 & 4 & 2\\ 2 & 1 & 2 & 4 \end{array}\right]\end{split}\]

Exercice: montrer que l’on obtiens la même expression de la matrice de masse pour un rectangle non aligné avec les axes.

6.4.3.3. second membre élémentaire

Comme dans le cas \(\mathcal{P}^{1}\), le second membre élémentaire s’écrit comme le produit de la matrice de masse par le vecteur \(F^{k}\) élémentaire des valeurs nodales de \(f\):

\[\mathbf{B}^{k}=\mathbf{M}^{k}\mathbf{F}^{k}\,\,\,\mbox{\, avec\, }\,\mathbf{F}^{k}=[f_{n_{1}},f_{n_{2}},f_{n_{3}},f_{n_{4}}]\]

6.4.4. Étude de la précision

Nous allons étudier le même cas qu’avec des traingles, mais avec des éléments \(\mathcal{Q}^{1}\). Le maillage est obtenu par transformation « quadrilatère courbe »

Le calcul a été effectué sur un maillage ayant le même nombre de noeuds (\(n_{1}=n_{2}=20\)) que celui utilisé précédemment pour les éléments \(\mathcal{P}^{1}\). La solution obtenue est tracée sur la figure (), que l’on peut comparer avec la solution \(\mathcal{P}^{1}\) sur un maillage équivalent (figure Fig. 6.27). On constate que les deux solutions sont quasiment identiques (le maillage étant relativement fin pour ce type de calcul).

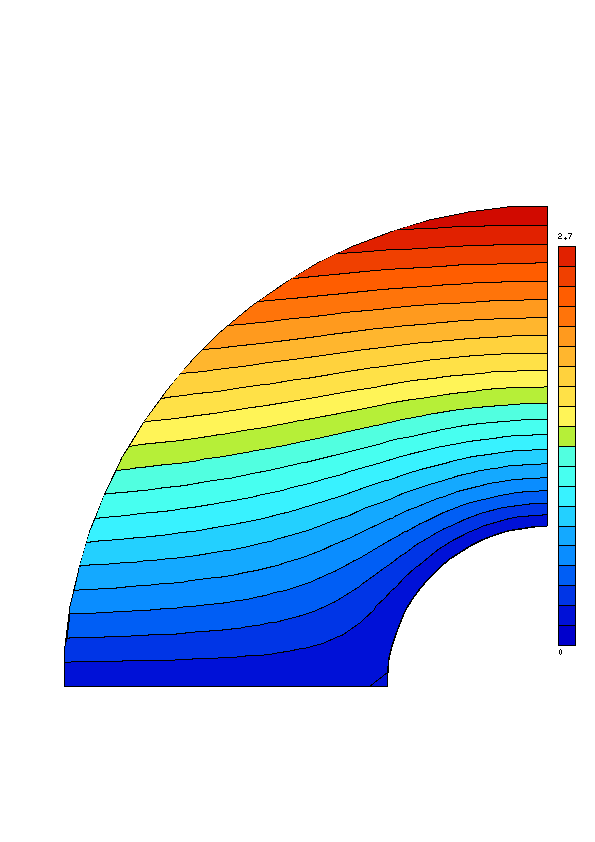
Fig. 6.33 solution \(\psi^{h}\) par éléments finis \(\mathcal{Q}^{1}\) avec un maillage équivalent au précédent

Pour étudier la précision, nous avons fait varier la taille caractéristique \(h\) des éléments du maillage et nous avons calculer l’erreur d’approximation \(\left\Vert \psi_{ex}-\psi^{h}\right\Vert\). Comme en \(\mathcal{P}^{1}\), nous avons calculer l’erreur élémentaire sur un élément à l’aide d’une intégration numérique utilisant 3 points de Gauss dans chaque direction.

Remarque: pour le calcul de l’erreur nous avons utilisé plus de points de Gauss \((3*3)\) que pour la calcul de la solution approchée (\(2*2)\), de façon à minimiser l’erreur numérique d’intégration par rapport à l’erreur d’approximation.

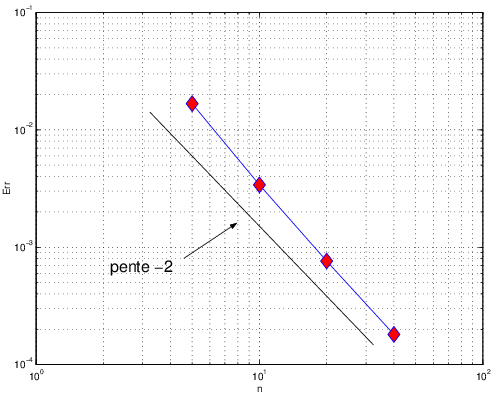
Fig. 6.34 Norme de l’erreur d’approximation \(\mathcal{Q}^{1}\) en fonction de \(n\propto h^{-1}\)

Nous avons donc construit une série de maillage de \(\Omega,\) avec une taille \(h\rightarrow0\) et un rapport d’aspect \(R\) constant en fixant un nombre de noeuds identiques sur les cotés lors de la génération du maillage: i.e. \(n_{1}=n_{2}=n\). Dans ce cas la taille des éléments \(h\) est proportionnelle à \(\frac{1}{n}\). On a donc tracé sur la figure Fig. 6.34, la norme de l’erreur en fonction de \(n\) et on vérifie que l’on obtiens une décroissance de l’erreur en \(n^{-2}\), soit en \(\theta(h^{2})\), ce qui montre que l’approximation par éléments finis \(\mathcal{Q}^{1}\) est d’ordre 2. En comparant la courbe obtenue avec celle de la figure Fig. 6.29, on constate que dans ce cas l’erreur est un peu plus faible avec les éléments \(\mathcal{Q}^{1}\) qu’avec les éléments \(\mathcal{P}^{1}\). C’est une constatation assez générale dans le cas de solutions régulières alignées avec le maillage.

notes

---

[1]

Hydrodynamics by Sir Horace LAMB, Dover Publications N.Y., 1953

[2]

FreeFem logiciel écrit par O. Pironneau, C. Prud’Homme et F. Hecht disponible sur le site https://freefem.org

[3]

dans les livres sur les éléments finis, on ne donne en générale que ces valeurs numériques!