10.1. Elément de référence, matrice élémentaire en 2D

Dans cette partie, nous étudierons la transformation vers l’élément de référence pour des maillages triangulaires \(P^1\) et quadrangulaires \(Q^1\). Pour des maillages quelconques, les logiciels utilisent une intégration numérique pour calculer les matrices élémentaires après transformation vers l’élément de référence. Cependant pour des maillages simples avec des triangles rectangles ou des rectangles alignés avec les axes, un calcul simple est possible que nous détaillerons à partir des relations générales.

10.1.1. Élément triangulaire \(P^1\)

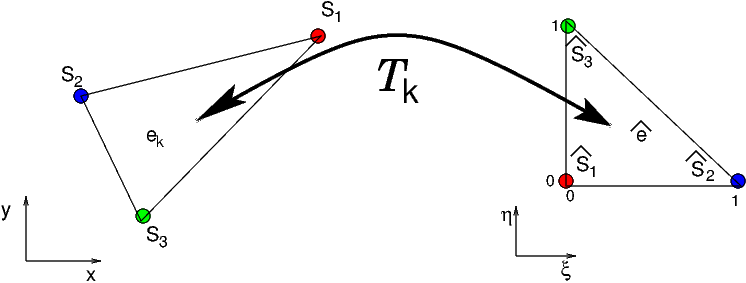
Cette transformation \(\mathcal{T}^{k}\) est une transformation affine:

\[\begin{split}\mathcal{T}_{k}\,\left\{ \begin{array}{ccc} e^{k} & \Longleftrightarrow & \hat{e}\\ \left[\begin{array}{c} x\\ y \end{array}\right] & \Longleftrightarrow & \left[\begin{array}{c} \xi\\ \eta \end{array}\right] \end{array}\right.\end{split}\]

dont l’expression de \((\xi\,\eta)\) en fonction de \((x,y)\) s’écrit :

\[\begin{split}\left[\begin{array}{c} \xi\\ \eta \end{array}\right]=\left[\begin{array}{cc} a_{11} & a_{12}\\ a_{21} & a_{22} \end{array}\right]\left[\begin{array}{c} x\\ y \end{array}\right]+\left[\begin{array}{c} b_{1}\\ b_{2} \end{array}\right]\end{split}\]

Les 6 coefficients de la transformation sont déterminés par les conditions de transformation des 3 sommets \(\{S_{i}\}_{i=1,3}\) de \(e_{k}\) vers les 3 sommets \(\{\hat{S}_{i}\}_{i=1,3}\) de l’élément de référence \(\hat{e}\):

\[\left\{ \hat{S}_{i}=T_{k}(S_{i})\right\} _{i=1,3}\]

Plutôt que de déterminer \((\xi\,\eta)\) en fonction de \((x,y)\), il est plus simple de calculer la transformation inverse \((x,y)\) en fonction de \((\xi\,\eta)\). C’est aussi une transformation affine, donc \(x(\xi\,\eta)\) est une combinaison linéaire des valeurs aux noeuds, i.e.des abscisses \(\{x_{n_{q}}\}\) des sommets de l’élément \(e_{k}\), et de même pour \(y(\xi,\eta)\).

On a donc

\[\begin{split}\begin{aligned} x=x_{n_{1}}N_{1}(\xi,\eta)+x_{n_{2}}N_{2}(\xi,\eta)+x_{n_{3}}N_{3}(\xi,\eta)\\ y=y_{n_{1}}N_{1}(\xi,\eta)+y_{n_{2}}N_{2}(\xi,\eta)+y_{n_{3}}N_{3}(\xi,\eta) \end{aligned}\end{split}\]

En notant que la somme des fonctions de forme est égale à 1 et que \(N_2 = \xi\) et \(N_3=\eta\), la transformation s’écrit:

\[\begin{split}\begin{aligned} x-x_{n_1}= (x_{n_{2}}-x_{n_1}) \xi + (x_{n_{3}}-x_{n_1}) \eta\\ y-y_{n_1}= (y_{n_{2}}-y_{n_1}) \xi + (y_{n_{3}}-y_{n_1}) \eta \end{aligned}\end{split}\]

ce qui permet de calculer facilement la matrice Jacobienne \(\mathbf{J}_{k} =\frac{D(x,y)}{D(\xi,\eta}\)

\[\begin{split}\mathbf{J}_{k}=\left[\begin{array}{cc} \frac{\partial x}{\partial\xi} & \frac{\partial x}{\partial\eta}\\ \frac{\partial y}{\partial\xi} & \frac{\partial y}{\partial\eta} \end{array}\right]=\left[\begin{array}{cc} (x_{n_{2}}-x_{n_{1}}) & (x_{n_{3}}-x_{n_{1}})\\ (y_{n_{2}}-y_{n_{1}}) & (y_{n_{3}}-x_{n_{1}}) \end{array}\right]\end{split}\]

et son déterminant qui vaut :

\[det(\mathbf{J}_{k}) = (\overrightarrow{S_1S_2} \wedge \overrightarrow{S_1S_3}).\vec{e}_z = 2 Aire(e_k) \]

Dans le cas de triangles quelconques, ces relations permettent effectivement le calcul des matrices élémentaires, mais avec des expressions qui deviennent complexes. Cependant, pour des maillages simples avec des triangles rectangles, un calcul simple est possible, que nous allons détaillé.

10.1.1.1. Cas de triangles rectangles

A titre d’exemple, calculons la transformation dans le cas des 2 triangles rectangles ci-dessous de côté \(h=0.5\), et dont les sommets sont numérotés à partir de l’angle droit.

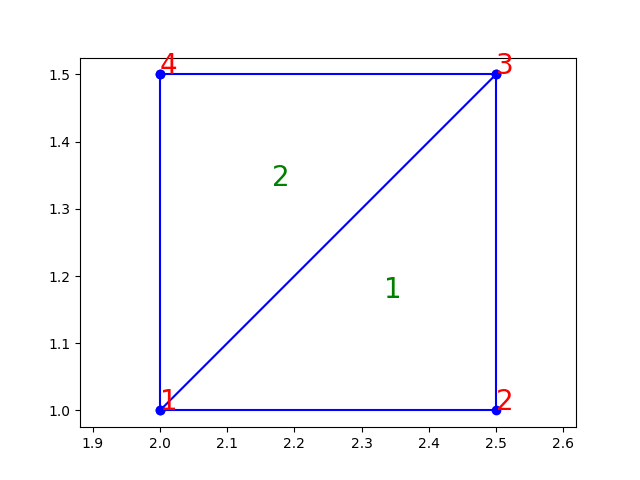
10.1.1.1.1. Element k=1 de sommets \(2,3,1\) et de coté \(h\)

La transformation s’écrit

\[\begin{split}\begin{aligned} x-x_{2}= - h \eta\\ y-y_{2}= h \xi \end{aligned}\end{split}\]

De même la matrice Jacobienne et son inverse:

\[\begin{split}\mathbf{J}_{k}= h \left[\begin{array}{cc} 0 & -1\\ 1 & 0 \end{array}\right] \mbox{ et } \mathbf{J}^{-1}_{k}= \frac{1}{h} \left[\begin{array}{cc} 0 & 1\\ -1 & 0 \end{array}\right] \end{split}\]

On vérifie facilement que

\[\begin{split} det(\mathbf{J}_{k}) = h^2 \mbox{ et } \mathbf{(J^{-1}_k})^{t} \mathbf{J^{-1}_k} = \frac{1}{h^2} \left[\begin{array}{cc} 1 & 0\\ 0 & 1 \end{array}\right]\end{split}\]

10.1.1.1.2. Element k=2 de sommets \(4,1,3\) et de coté \(h\)

La transformation s’écrit

\[\begin{split}\begin{aligned} x-x_{4}= h \eta\\ y-y_{4}= -h \xi \end{aligned}\end{split}\]

De même la matrice Jacobienne et son inverse:

\[\begin{split}\mathbf{J}_{k}= h \left[\begin{array}{cc} 0 & 1\\ -1 & 0 \end{array}\right] \mbox{ et } \mathbf{J}^{-1}_{k}= \frac{1}{h} \left[\begin{array}{cc} 0 & -1\\ 1 & 0 \end{array}\right] \end{split}\]

On vérifie facilement que

\[\begin{split} det(\mathbf{J}_{k}) = h^2 \mbox{ et } \mathbf{J^{-1}_k} (\mathbf{J^{-1}_k})^t = \frac{1}{h^2} \left[\begin{array}{cc} 1 & 0\\ 0 & 1 \end{array}\right]\end{split}\]

On obtiens donc le même résultat que pour l’élément \(k=1\). On peut vérifier que c’est vrai pour tout triangle rectangle de coté h.

10.1.1.1.3. Cas général d’un triangle rectangle quelconque

On obtient des résultats similaires dans le cas de triangles rectangles ci-dessous, de côté \(h=0.5\), et dont les cotés ont subis une rotation d’angle \(\theta\).

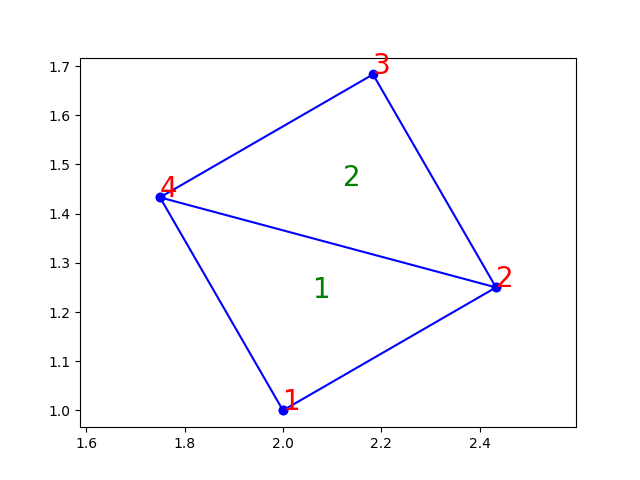
La transformation (pour \(k=1\)) correspond à une translation suivie d’une rotation d’angle \(\theta\) (le cas précédent correspond à \(\theta= \pi\) ).

\[\begin{split}\left[\begin{array}{c} x - x_{n_1}\\ y - y_{n_1} \end{array}\right]= h \left[\begin{array}{cc} \cos\theta & -\sin\theta\\ \sin\theta & \cos\theta \end{array}\right]\left[\begin{array}{c} \xi\\ \eta \end{array}\right]\end{split}\]

La matrice Jacobienne correspond à la matrice de rotation d’angle \(\theta\) multipliée par \(h\)

\[\begin{split} \mathbf{J_k} = h \left[\begin{array}{cc} \cos\theta & -\sin\theta\\ \sin\theta & \cos\theta \end{array}\right]\end{split}\]

dont l’inverse est égale à

\[\begin{split} \mathbf{J_k} = \frac{1}{h} \left[\begin{array}{cc} \cos\theta & \sin\theta\\ -\sin\theta & \cos\theta \end{array}\right]\end{split}\]

On vérifie alors facilement que

\[\begin{split} det(\mathbf{J}_{k}) = h^2 \mbox{ et } \mathbf{J^{-1}_k} (\mathbf{J^{-1}_k})^t = \frac{1}{h^2} \left[\begin{array}{cc} 1 & 0\\ 0 & 1 \end{array}\right]\end{split}\]

10.1.1.2. Calcul des matrices élémentaires

La forme générale de la matrice élémentaire de raideur \(\mathbf{K^k}\) sur l’élément de référence s’écrit:

\[\begin{split}\mathbf{K}_{pq}^{k}=\frac{\det(\mathbf{J}_{k})}{2} \left[\begin{array}{cc} \frac{\partial N_{p}}{\partial\xi} & \frac{\partial N_{p}}{\partial\eta}\end{array}\right] (\mathbf{J}_{k}^{-1}).(\mathbf{J}_{k}^{-1})^{t} \left[\begin{array}{c} \frac{\partial N_{q}}{\partial\xi}\\ \frac{\partial N_{q}}{\partial\eta}\end{array}\right]\end{split}\]

Pour un triangle rectangle de coté \(h\) numéroté à partir de l’angle droit, en utilisant le calcul précédent, on montre facilement que :

\[\begin{split} \mathbf{K}^k = \frac{1}{2} \left[\begin{array}{ccc} 2 & -1 & -1 \\ -1 & 1 & 0 \\ -1 & 0 & 1 \end{array}\right] \end{split}\]

qui vérifie les propriétés de symétrie, avec la somme des lignes égale à zéro.

De même pour la matrice élémentaire de masse, la forme générale sur l’élément de référence s’écrit :

\[ \mathbf{M}_{pq}^{k} = \det(\mathbf{J}_{k}) \iint_{e_k} N_p N_q d\xi d\eta = \det(\mathbf{J}_{k}) \int_0^1 \int_0^{1-\xi} N_p(\xi,\eta) N_q(\xi,\eta) d\xi d\eta \]

En calculant les 2 intégrale suivantes:

\[\int_{0}^{1}\int_{0}^{1-\xi}\eta\xi\,d\eta d\xi=\frac{1}{24},\,\int_{0}^{1}\int_{0}^{1-\xi}\xi^{2}\,d\eta d\xi=\frac{1}{12}\]

on en déduit, en utilisant les propriétés de symétrie

\[\begin{split}\mathbf{M}^{k}=\frac{aire_{k}}{12} \left[\begin{array}{ccc}2 & 1 & 1\\ 1 & 2 & 1\\1 & 1 & 2 \end{array}\right]\end{split}\]

Cette matrice vérifie les propriétés de symétrie, avec la somme des lignes égale à \(\frac{aire_k}{3}\) car $\(\int_{0}^{1}\int_{0}^{1-\eta} \eta d\xi d\eta =\int_{0}^{1}\int_{0}^{1-\xi} \xi d\eta d\xi= \frac{1}{6} \)$

10.1.1.3. Calcul du second membre élémentaire

Le second membre élémentaire pour une fonction \(f(x,y)\) s’écrit sur l’élément de référence:

\[\mathbf{B}_{p}^{k}= \det(\mathbf{J}_{k}) \iint_{e_k} \mathbf{f}.N_p(\xi,\eta)\,d\xi d\eta\]

Pour calculer l’expression de \(\mathbf{f}\) sur l’élément de référence, on utilise son interpolation \(\mathbf{f^h}\) par éléments finis, ce qui donne sur l’élément de référence:

\[ \mathbf{f^h}(\xi,\eta) = f_{n_1} N_1(\xi,\eta) + f_{n_2} N_2(\xi,\eta) + f_{n_3} N_3(\xi,\eta) \]

où \(f_{n_1},f_{n_2},f_{n_3}\) sont les valeurs nodales de \(\mathbf{f}\) aux 3 sommets de l’élément.

La valeur du vecteur second membre élémentaire \(\mathbf{B}^k\) se calcule dont facilement à partir de la matrice élémentaire de masse:

\[\begin{split}\mathbf{B}^{k} = \mathbf{M}^{k} \left[\begin{array}{c} f_{n_1} \\ f_{n_2} \\ f_{n_3} \end{array}\right]\end{split}\]

10.1.2. Élément quadrangulaire \(Q^1\)

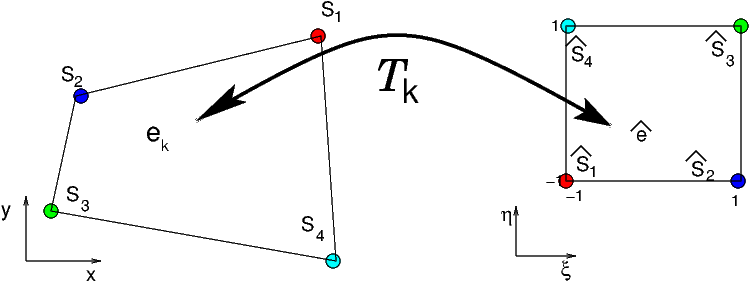
Cette transformation \(\mathcal{T}^{k}\) est une transformation bilinéaire (i.e. le produit d’un polynôme de degré 1 en \(\xi\) par un polynôme de degré 1 en \(\eta\)):

\[\begin{split}\mathcal{T}_{k}\,\left\{ \begin{array}{ccc} e^{k} & \Longleftrightarrow & \hat{e}=[-1,+1]\times[-1,+1]\\ \left[\begin{array}{c} x\\ y \end{array}\right] & \Longleftrightarrow & \left[\begin{array}{c} \xi\\ \eta \end{array}\right] \end{array}\right.\end{split}\]

dont l’expression de \((\xi\,\eta)\) en fonction de \((x,y)\) s’écrit :

\[\begin{split}\left[\begin{array}{c}\xi\\ \eta \end{array}\right]= \left[\begin{array}{c} (a_{11} x + a_{12}) \times (b_{11} y + b_{12})\\ (a_{21} x + a_{22}) \times (b_{21} y + b_{22}) \end{array}\right] \end{split}\]

Les 8 coefficients de la transformation sont déterminés par les conditions de transformation des 4 sommets \(\{S_{i}\}_{i=1,4}\) de \(e_{k}\) vers les 4 sommets \(\{\hat{S}_{i}\}_{i=1,4}\) de l’élément de référence \(\hat{e}\):

\[\left\{ \hat{S}_{i}=T_{k}(S_{i})\right\} _{i=1,4}\]

Plutôt que de déterminer \((\xi\,\eta)\) en fonction de \((x,y)\), il est plus simple de calculer la transformation inverse \((x,y)\) en fonction de \((\xi\,\eta)\). C’est aussi une transformation bilénaire, donc \(x(\xi\,\eta)\) est une combinaison linéaire des valeurs aux noeuds, i.e.des abscisses \(\{x_{n_{q}}\}\) des sommets de l’élément \(e_{k}\), et de même pour \(y(\xi,\eta)\).

On a donc

\[\begin{split}\begin{aligned} x=x_{n_{1}}N_{1}(\xi,\eta)+x_{n_{2}}N_{2}(\xi,\eta)+x_{n_{3}}N_{3}(\xi,\eta)+x_{n_{4}}N_{4}(\xi,\eta)\\ y=y_{n_{1}}N_{1}(\xi,\eta)+y_{n_{2}}N_{2}(\xi,\eta)+y_{n_{3}}N_{3}(\xi,\eta)+y_{n_{4}}N_{4}(\xi,\eta) \end{aligned}\end{split}\]

Les fonctions \(\{N_{q}(\xi,\eta)\}_{q=1,4}\) sont les fonctions de forme de l’élément \(\mathcal{Q}^{1}\): ce sont des fonctions bilinéaires qui vérifient:

\[N_{q}(\hat{S}_{p})=\delta_{p,q}\,\mbox{\, \, pour\, }\,p,q=1,4\]

Ce sont les polynômes de Lagrange de degré 1, dont l’expression est la suivante:

\[\begin{split}\begin{aligned} N_{1}(\xi,\eta)=\frac{1}{4}(1-\xi)(1-\eta)\\ N_{2}(\xi,\eta)=\frac{1}{4}(1+\xi)(1-\eta)\\ N_{3}(\xi,\eta)=\frac{1}{4}(1+\xi)(1+\eta)\\ N_{4}(\xi,\eta)=\frac{1}{4}(1-\xi)(1+\eta)\end{aligned}\end{split}\]

En notant que la somme des fonctions de forme est égale à 1, la transformation s’écrit:

\[\begin{split}\begin{aligned} x-x_{n_1}= (x_{n_{2}}-x_{n_1}) N_2(\xi,\eta) + (x_{n_{3}}-x_{n_1}) N_3(\xi,\eta) + (x_{n_{4}}-x_{n_1}) N_4(\xi,\eta)\\ y-y_{n_1}= (y_{n_{2}}-y_{n_1}) N_2(\xi,\eta) + (y_{n_{3}}-y_{n_1}) N_3(\xi,\eta) + (y_{n_{4}}-y_{n_1}) N_4(\xi,\eta) \end{aligned}\end{split}\]

ce qui permet de calculer la matrice Jacobienne \(\mathbf{J}_{k} =\frac{D(x,y)}{D(\xi,\eta}\)

On constate que contrairement à l’élément \(\mathcal{P}^{1}\), la matrice jacobienne de cette transformation n’est pas constante, ni son déterminant.

Dans le cas de quadrangle quelconque, on utilise en général une intégration numérique pour calculer les matrices élémentaires. Dans le cas d’éléments rectangulaires, un calcul analytique simple est cependant possible.

10.1.2.1. Cas d’éléments rectangulaires alignés avec les axes

Calculons la transformation dans le cas du rectangle ci-dessous de côté \(h=0.5\), et dont les sommets sont numérotés à partir du noeud en bas à gauche (sommet 1).

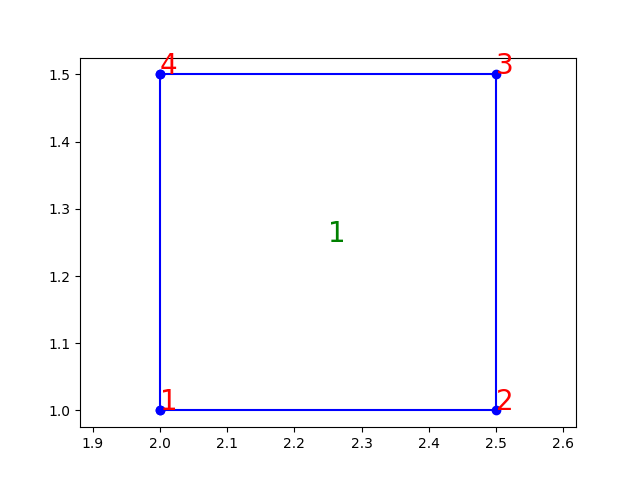
Dans ce cas la transformation s’écrit

\[\begin{split}\begin{aligned} x-x_{1}= h \frac{(1+\eta)}{2}\\ y-y_{1}= h \frac{(1+\xi)}{2} \end{aligned}\end{split}\]

De même la matrice Jacobienne et son inverse:

\[\begin{split}\mathbf{J}_{k}= \frac{h}{2} \left[\begin{array}{cc} 1 & 0\\ 0 & 1 \end{array}\right] \mbox{ et } \mathbf{J}^{-1}_{k}= \frac{2}{h} \left[\begin{array}{cc} 1 & 0\\ 0 & 1 \end{array}\right] \end{split}\]

On vérifie facilement que

\[\begin{split} det(\mathbf{J}_{k}) = \frac{h^2}{4} \mbox{ et } \mathbf{(J^{-1}_k})^{t} \mathbf{J^{-1}_k} = \frac{4}{h^2} \left[\begin{array}{cc} 1 & 0\\ 0 & 1 \end{array}\right]\end{split}\]

10.1.2.2. Calcul des matrices élémentaires

La forme générale de la matrice élémentaire de raideur \(\mathbf{K^k}\) sur l’élément de référence s’écrit:

\[\begin{split}\mathbf{K}_{pq}^{k}= \iint_{\hat{e}} \left[\begin{array}{cc} \frac{\partial N_{p}}{\partial\xi} & \frac{\partial N_{p}}{\partial\eta}\end{array}\right] (\mathbf{J}_{k}^{-1}).(\mathbf{J}_{k}^{-1})^{t} \left[\begin{array}{c} \frac{\partial N_{q}}{\partial\xi}\\ \frac{\partial N_{q}}{\partial\eta}\end{array}\right] \det(\mathbf{J}_{k}) d\xi d\eta\end{split}\]

Pour un rectangle de coté \(h\) aligné avec les axes et numéroté à partir de l’angle droit, la matrice jacobienne étant constante, on calcule analytiquement que :

\[\begin{split} \mathbf{K}^k = \frac{1}{6} \left[\begin{array}{cccc} 4 & -1 & -2 & -1\\ -1 & 4 & -1 & -1\\ -2 & -1 & 4 & -1\\ -1 &-2 & -1 & 4 \\ \end{array}\right] \end{split}\]

qui vérifie les propriétés de symétrie, avec la somme des lignes égale à zéro.

De même pour la matrice élémentaire de masse, la forme générale sur l’élément de référence s’écrit :

\[ \mathbf{M}_{pq}^{k} = \iint_{e_k} N_p N_q \det(\mathbf{J}_{k}) d\xi d\eta = \int_{-1}^{+1} \int_{-1}^{+1} N_p(\xi,\eta) N_q(\xi,\eta) \det(\mathbf{J}_{k}) d\xi d\eta \]

Dans le cas d’un triangle rectangle de cotés \(h\) alignés suivant les axes \(x\) et \(y\), le Jacobien de la transformation est constant et on peut calculer simplement la matrice de masse:

\[\begin{split}\mathbf{M}_{pq}^{k}=\frac{h^2}{36}\left[\begin{array}{cccc} 4 & 2 & 1 & 2\\ 2 & 4 & 2 & 1\\ 1 & 2 & 4 & 2\\ 2 & 1 & 2 & 4\end{array}\right]\end{split}\]

Cette matrice vérifie les propriétés de symétrie, avec la somme des lignes égale à \(\frac{aire_k}{4}\) car

\[\int_{-1}^{+1}\int_{-1}^{+1} N_1 d\xi d\eta = \int_{-1}^{+1}\int_{-1}^{+1} N_2 d\xi d\eta = \int_{-1}^{+1}\int_{-1}^{+1} N_3 d\xi d\eta = \int_{-1}^{+1}\int_{-1}^{+1} N_4 d\xi d\eta = 2 \times\frac{1}{4} \]

10.1.2.3. Calcul du second membre élémentaire

Le second membre élémentaire pour une fonction \(f(x,y)\) s’écrit sur l’élément de référence:

\[\mathbf{B}_{p}^{k}= \iint_{e_k} \mathbf{f}.N_p(\xi,\eta) \det(\mathbf{J}_{k}) \,d\xi d\eta\]

Pour calculer l’expression de \(\mathbf{f}\) sur l’élément de référence, on utilise son interpolation \(\mathbf{f^h}\) par éléments finis, ce qui donne sur l’élément de référence:

\[ \mathbf{f^h}(\xi,\eta) = f_{n_1} N_1(\xi,\eta) + f_{n_2} N_2(\xi,\eta) + f_{n_3} N_3(\xi,\eta) + f_{n_4} N_4(\xi,\eta) \]

où \(f_{n_1},f_{n_2},f_{n_3},f_{n_4}\) sont les valeurs nodales de \(\mathbf{f}\) aux 4 sommets de l’élément.

La valeur du vecteur second membre élémentaire \(\mathbf{B}^k\) se calcule dont facilement à partir de la matrice élémentaire de masse:

\[\begin{split}\mathbf{B}^{k} = \mathbf{M}^{k} \left[\begin{array}{c} f_{n_1} \\ f_{n_2} \\ f_{n_3}\\f_{n_4} \end{array}\right]\end{split}\]