Interpolation 1D par élements finis

9.1. Interpolation 1D par élements finis#

cours master M1 mécanique: éléments finis (Marc Buffat , UCB Lyon 1)

%matplotlib inline
import sys,os
import numpy as np
import scipy as sp
import matplotlib
import matplotlib.pyplot as plt
from random import random
from validation.validation import check_function
from IPython.display import display, Markdown, Latex
def printmd(string):
    display(Markdown(string))
# test si numero étudiant spécifier
try: NUMERO_ETUDIANT
except NameError: NUMERO_ETUDIANT = None 
if type(NUMERO_ETUDIANT) is not int :
    NUMERO_ETUDIANT = 12345
    NOM = "test"
    PRENOM = "test"
    #raise AssertionError("NUMERO_ETUDIANT non défini")
# parametres spécifiques
_uid_    = NUMERO_ETUDIANT
np.random.seed(_uid_)
_a_ = 1+np.random.randint(3)
_b_ = 1+np.random.randint(3)
_L_ = 1.+np.random.randint(5)
printmd("## Etudiant {} {}  id={}".format(NOM,PRENOM,NUMERO_ETUDIANT))
printmd("### fonction à interpoler f(x) = {} sin({} x) sur l'intervalle [0,L] avec L={}".format(_a_,_b_,_L_))

Etudiant test test id=12345

fonction à interpoler f(x) = 3 sin(2 x) sur l’intervalle [0,L] avec L=2.0

9.1.1. Fonction à interpoler f(x)#

Ecrire la fonction f(x) à interpoler, et définir la longueur de l’intervalle dans la variable L

## BEGIN SOLUTION
L = _L_
def f(x):
    return _a_*np.sin(_b_*x)
## END SOLUTION

assert(L == _L_)
assert(np.abs(f(0))<1.0e-5)
assert(np.abs(f(np.pi/(2*_b_))-_a_)<1.0e-5)
printmd("### Validation OK")

Validation OK

9.1.2. Interpolation par élements finis \(P^1\)#

On choisit de faire une interpolation avec des polynômes \(P^1\).

Pour cela on définit les deux fonctions de forme \(N_1(\chi)\) et \(N_2(\chi)\) sur l’intervalle de référence \([0,1]\)

9.1.2.1. fonctions de forme sur [0,1]#

Ecrire les 2 fonctions de forme \(P^1\) sur \([0,1]\): N1(xsi) et N2(xsi)

def N1(xsi):
    ## BEGIN SOLUTION
    return 1-xsi
    ## END SOLUTION
def N2(xsi):
    ## BEGIN SOLUTION
    return xsi
    ## END SOLUTION

assert((N1(0.)==1.) and (N1(1.)==0.0))
assert((N2(0.)==0.) and (N2(1.)==1.0))
printmd("## Validation OK")

Validation OK

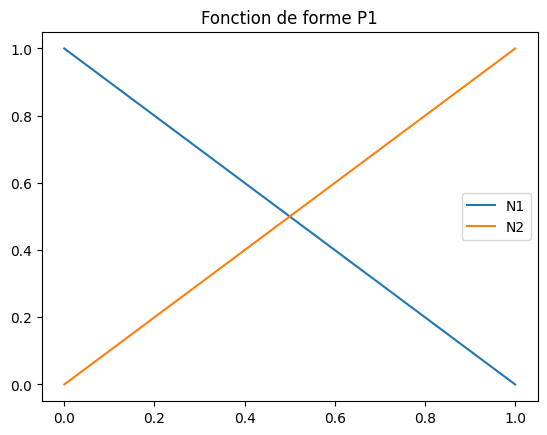
9.1.2.2. tracer les 2 fonctions de forme sur [0,1]#

avec un titre et des labels

## BEGIN SOLUTION
X=np.linspace(0,1,21)
plt.plot(X,N1(X),label="N1")
plt.plot(X,N2(X),label="N2")
plt.title("Fonction de forme P1")
plt.legend();
## END SOLUTION
../../../_images/e40dbc4da9f210c8ddef0c243d28f4483a0fec3ad49d6e9f5efa57df575dfa26.png

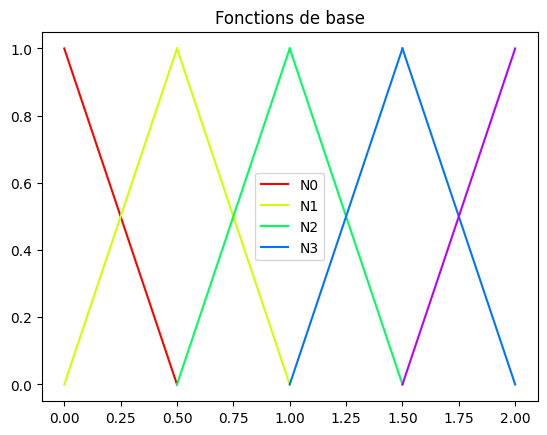
9.1.2.3. Fonctions de base P1#

Ecrire une fonction TraceBaseP1(Ne,L) qui, sur sur un maillage de Ne elements de \([0,L]\), trace toutes les fonctions de base.

La fonction devra utiliser les 2 fonctions de forme précédentes (en utilisant un changement de variable)

def TraceBaseP1(Ne,L):
    '''trace toutes les fonctions de base P1 sur un maillage [0,L] de Ne elts'''
    ## BEGIN SOLUTION
    h   = L/Ne
    Xp  = np.linspace(0,L,Ne+1)
    Xsi = np.linspace(0,1,20)
    Phi1 = N1(Xsi)
    Phi2 = N2(Xsi)
    cols = plt.cm.get_cmap('hsv', Ne+2)
    for k in range(Ne):
        X = Xp[k] + Xsi*h
        plt.plot(X,Phi1,color=cols(k),label="N{}".format(k))
        plt.plot(X,Phi2,color=cols(k+1))
    plt.legend()
    plt.title("Fonctions de base")
    return
    ## END SOLUTION

# verification
TraceBaseP1(4,L)

/tmp/ipykernel_1319102/606310683.py:9: MatplotlibDeprecationWarning: The get_cmap function was deprecated in Matplotlib 3.7 and will be removed in 3.11. Use ``matplotlib.colormaps[name]`` or ``matplotlib.colormaps.get_cmap()`` or ``pyplot.get_cmap()`` instead.
  cols = plt.cm.get_cmap('hsv', Ne+2)
../../../_images/b7b0a48e4d5754d0df6c3c4e3cbbe75717218c82860ede61b96c1836e12cda91.png 
'''verification utilisation des fonctions de forme'''
orig_N1 = N1
orig_N2 = N2
del N2,N1
try:
    TraceBaseP1(4,L)
except NameError as error:
    printmd("### Validation OK")
    pass
else:
    raise AssertionError("erreur n'utilise pas les fonctions de forme")
finally:
    N1 = orig_N1    
    N2 = orig_N2

Validation OK

9.1.2.4. interpolation P1#

écrire une fonction interpolP1(x,Yp,L) qui calcule l’interpolation en x de la fonction \(f(x)\) donnée par ses valeurs nodales \(Yp\) sur un maillage équiréparti du segment \([0,L]\)

La fonction doit utiliser les fonctions de forme N1,N2

def interpolP1(x,Yp,L):
    ## BEGIN SOLUTION
    n = Yp.size
    ne = n-1
    Xe = np.linspace(0,L,ne+1)
    k = np.searchsorted(Xe,x,side='right')
    if k > ne: k=ne
    k = k-1
    xsi = (x-Xe[k])/(Xe[k+1]-Xe[k])
    yi = Yp[k]*N1(xsi)+Yp[k+1]*N2(xsi)
    return yi
    ## END SOLUTION

# verification sur une fonction lineaire! on doit trouver 0.5
Ne = 3
Xp = np.linspace(0,L,2*Ne+1)
Yp = Xp
print(interpolP1(0.5,Yp,L))

0.5

Ne = 4
Xp = np.linspace(0,L,Ne+1)
Yp = f(Xp)
''' verification aux pts d interpolation '''
for i,x in enumerate(Xp):
    yi = interpolP1(x,Yp,L)
    assert(np.abs(yi-Yp[i])<1.e-10)
'''verification utilisation des fonctions de forme'''
orig_N1 = N1
orig_N2 = N2
del N2,N1
try:
    interpolP1(0.5,Yp,L)
except NameError as error:
    printmd("## Validation OK")
    pass
else:
    raise AssertionError("erreur n'utilise pas les fonctions de forme")
finally:
    N1 = orig_N1    
    N2 = orig_N2

Validation OK

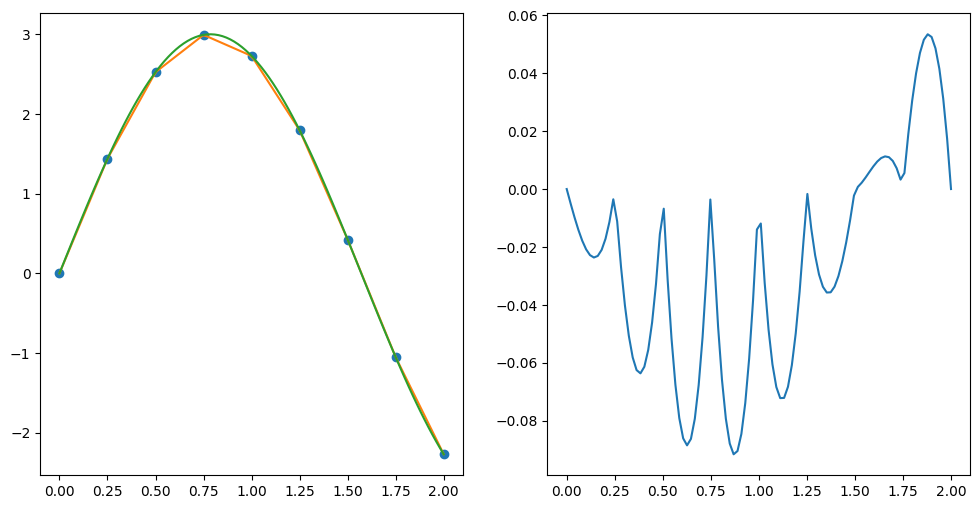
9.1.2.5. tracé de l’interpolation P1#

  • tracer l’interpolation et comparer avec la fonction f(x).

  • tracer l’erreur (ecart)

## BEGIN SOLUTION
Ne=8
Xp=np.linspace(0,L,Ne+1)
Yp=f(Xp)
X = np.linspace(0,L,100)
Y = [interpolP1(x,Yp,L) for x in X]
Ye = f(X)
# tracer
plt.figure(figsize=(12,6))
plt.subplot(1,2,1)
plt.plot(Xp,Yp,'o')
plt.plot(X,Y)
plt.plot(X,Ye)
plt.subplot(1,2,2)
plt.plot(X,Y-Ye);
## END SOLUTION
../../../_images/3f4cf30b652d4f310dd2e6b4e8eb62c0bfc3f455ca4bfa928b4bf31bfd7baea3.png

9.1.2.6. évolution de l’erreur#

  • écrire une fonction erreurP1(F,L,ne) qui calcule la norme (norme du max) de l’erreur d’interpolation entre une fonction F(x) et son interpolation sur ne elements P1.

  • étudier l’évolution de cette erreur d’interpolation en fonction de ne.

  • en déduire la précision (on pourra utiliser polyfit de numpy)

def erreurP1(F,L,ne):
    '''calcul erreur interpolation (norme du max) de la fonction F sur [0,L] avec ne elts'''
    ## BEGIN SOLUTION
    Xp= np.linspace(0,L,ne+1)
    Yp= F(Xp)
    X = np.linspace(0,L,100)
    Y = [interpolP1(x,Yp,L) for x in X]
    Ye = F(X)
    Err=np.max(np.abs(Y-Ye))
    return Err
    ## END SOLUTION

# vérification que l'erreur décroit en fct de Ne
print("erreur Ne=4,8 ",erreurP1(f,L,4),erreurP1(f,L,8),"Gain:",erreurP1(f,L,4)/erreurP1(f,L,8))

erreur Ne=4,8  0.3662500790238097 0.09160385116255165 Gain: 3.9981952109622165

'''test sur une fonction lineaire'''
Fl = lambda x:2*x+1
assert np.abs(erreurP1(Fl,L,4)) < 1.e-8
assert np.abs(erreurP1(Fl,L,8)) < 1.e-8
printmd("### Validation OK")

Validation OK

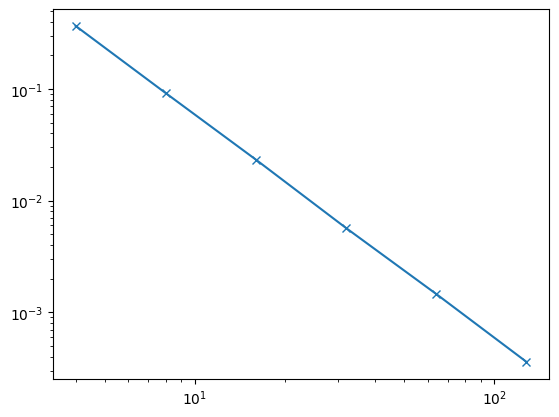
9.1.2.7. Erreur d’interpolation#

En utilisant la fonction erreurP1 tracer l’évolution de l’erreur en fonction de Ne et calculer la précision (ordre) de l’interpolation

## BEGIN SOLUTION
NE=[4,8,16,32,64,128]
Err=np.zeros(len(NE))
for i,ne in enumerate(NE):
   Err[i]=erreurP1(f,L,ne)
#
plt.loglog(NE,Err,'x-')
pente=np.round(np.polyfit(np.log(NE),np.log(Err),deg=1)[0],2)
print("ordre ",-pente)
## END SOLUTION

ordre  2.0
../../../_images/f3e03e63669e6e4231b7e2751b788254628b2127d695d2d2b1d3b6a2fec8c480.png

9.1.2.8. Commentaires#

écrire vos commentaires et faire une analyse (2 pts)

=== BEGIN ANSWER ===

=== END ANSWER ===

9.1.3. Interpolation par élements finis \(P^2\)#

On choisit maintenant de faire une interpolation avec des polynômes \(P^2\).

Pour cela on définit les trois fonctions de forme \(N_1(\chi)\), \(N_2(\chi)\) , \(N_3(\chi)\) sur l’intervalle de référence \([0,1]\) associées aux 3 points d’interpolation \(\chi=0 , \frac{1}{2}, 1\)

9.1.3.1. fonctions de forme sur [0,1]#

Ecrire les 3 fonctions de forme N1(xsi),N2(xsi) et N3(xsi)

def N1(xsi):
    ## BEGIN SOLUTION
    return 2*(1-xsi)*(0.5-xsi)
    ## END SOLUTION
def N2(xsi):
    ## BEGIN SOLUTION
    return 4*xsi*(1-xsi)
    ## END SOLUTION
def N3(xsi):
    ## BEGIN SOLUTION
    return 2*xsi*(xsi-0.5)
    ## END SOLUTION

assert((N1(0.)==1.) and (N1(1.)==0.0) and (N1(0.5)==0.))
assert((N2(0.)==0.) and (N2(1.)==0.0) and (N2(0.5)==1.))
assert((N3(0.)==0.) and (N3(1.)==1.0) and (N3(0.5)==0.))
printmd("## Validation OK")

Validation OK

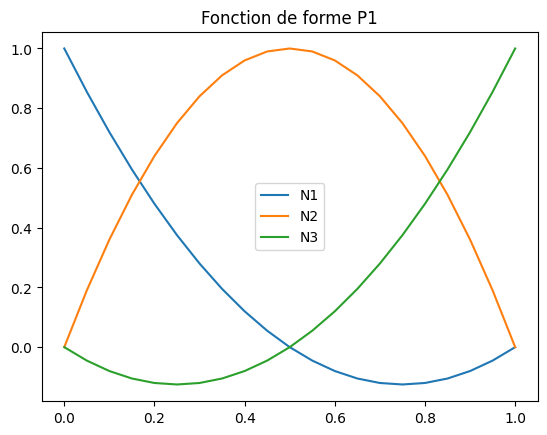
9.1.3.2. tracer les fonctions de base sur [0,1]#

## BEGIN SOLUTION
X=np.linspace(0,1,21)
plt.plot(X,N1(X),label="N1")
plt.plot(X,N2(X),label="N2")
plt.plot(X,N3(X),label="N3")
plt.title("Fonction de forme P1")
plt.legend();
## END SOLUTION
../../../_images/7b84fe860b7fd4dbd55bfee132b0485d18edc55991b99ecca20511a89ce83d6a.png

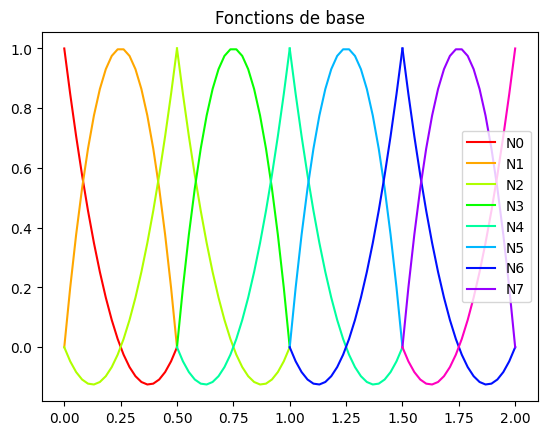
9.1.3.3. Fonctions de base P2#

Ecrire une fonction TraceBaseP2() qui sur sur un maillage de Ne elements sur [0,L][0,L] trace les fonctions de base. La fonction devra utiliser les fonctions de forme précédentes

def TraceBaseP2(Ne,L):
    '''trace les fonctions de base P2 sur un maillage [0,L] de Ne elts'''
    ## BEGIN SOLUTION
    h   = L/Ne
    Xp  = np.linspace(0,L,Ne+1)
    Xsi = np.linspace(0,1,20)
    Phi1 = N1(Xsi)
    Phi2 = N2(Xsi)
    Phi3 = N3(Xsi) 
    cols = plt.cm.get_cmap('hsv', 2*Ne+2)
    for k in range(Ne):
        X = Xp[k] + Xsi*h
        plt.plot(X,Phi1,color=cols(2*k),label="N{}".format(2*k))
        plt.plot(X,Phi2,color=cols(2*k+1),label="N{}".format(2*k+1))
        plt.plot(X,Phi3,color=cols(2*k+2))
    plt.legend()
    plt.title("Fonctions de base")
    return
    ## END SOLUTION

# verification
TraceBaseP2(4,L)

/tmp/ipykernel_1319102/1927418173.py:10: MatplotlibDeprecationWarning: The get_cmap function was deprecated in Matplotlib 3.7 and will be removed in 3.11. Use ``matplotlib.colormaps[name]`` or ``matplotlib.colormaps.get_cmap()`` or ``pyplot.get_cmap()`` instead.
  cols = plt.cm.get_cmap('hsv', 2*Ne+2)
../../../_images/55635ced06aff287c4b4b6ccda7f671b301b0fb50a2d39869ea55a09d1ceaafb.png 
'''verification utilisation des fonctions de forme'''
orig_N1 = N1
orig_N2 = N2
orig_N3 = N3
del N3,N2,N1
try:
    TraceBaseP2(4,L)
except NameError as error:
    printmd("### Validation OK")
    pass
else:
    raise AssertionError("erreur n'utilise pas les fonctions de forme")
finally:
    N1 = orig_N1    
    N2 = orig_N2
    N3 = orig_N3

Validation OK

9.1.3.4. interpolation P2#

écrire une fonction interpolP2 qui calcule l’interpolation en x de la fonction \(f(x)\) donnée par ses valeurs nodales \(Yp\) sur un maillage équirépartir du segment \([0,L]\). La fonction doit utiliser les fonctions de forme.

def interpolP2(x,Yp,L):
    ## BEGIN SOLUTION
    n = Yp.size
    ne = (n-1)//2
    Xe = np.linspace(0,L,ne+1)
    k = np.searchsorted(Xe,x,side='right')
    if k > ne: k=ne
    k = k-1
    xsi = (x-Xe[k])/(Xe[k+1]-Xe[k])
    yi = Yp[2*k]*N1(xsi)+Yp[2*k+1]*N2(xsi)+Yp[2*k+2]*N3(xsi)
    return yi
    ## END SOLUTION

# verification sur une fonction quadratique on doit trouver 0.25
Ne = 3
Xp = np.linspace(0,L,2*Ne+1)
Yp = Xp*Xp
print(interpolP2(0.5,Yp,L))

0.25

Ne = 4
Xp = np.linspace(0,L,2*Ne+1)
Yp = f(Xp)
''' verification aux pts d interpolation '''
for i,x in enumerate(Xp):
    yi = interpolP2(x,Yp,L)
    assert(np.abs(yi-Yp[i])<1.e-10)
'''verification utilisation des fonctions de forme'''
orig_N1 = N1
orig_N2 = N2
orig_N3 = N3
del N3,N2,N1
try:
    interpolP2(0.5,Yp,L)
except NameError as error:
    printmd("## Validation OK")
    pass
else:
    raise AssertionError("erreur n'utilise pas les fonctions de forme")
finally:
    N1 = orig_N1    
    N2 = orig_N2
    N3 = orig_N3

Validation OK

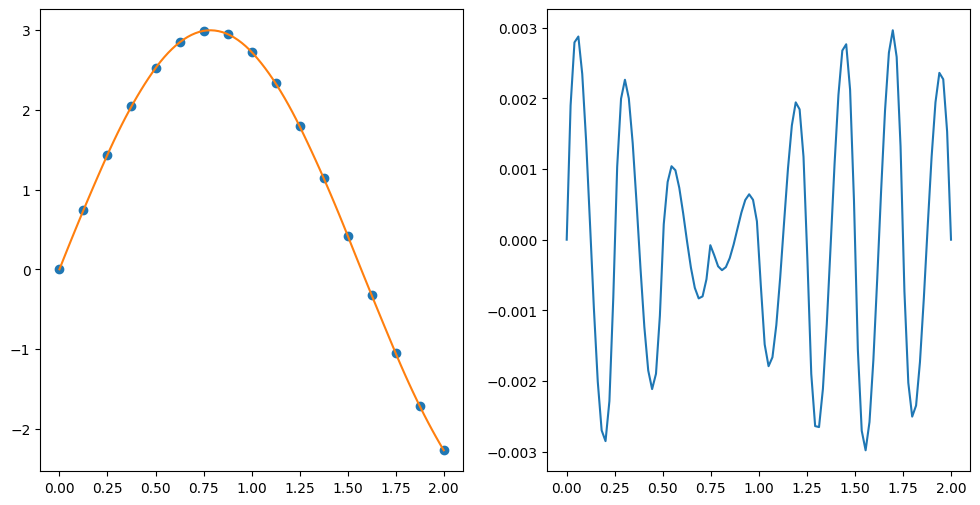
9.1.3.5. tracé interpolation#

tracer la fonction interpolée de f(x) ainsi que l’erreur d’interpolation

## BEGIN SOLUTION
Ne=8
Xp=np.linspace(0,L,2*Ne+1)
Yp=f(Xp)
X = np.linspace(0,L,100)
Y = [ interpolP2(x,Yp,L) for x in X]
Ye = f(X)
# tracer
plt.figure(figsize=(12,6))
plt.subplot(1,2,1)
plt.plot(Xp,Yp,'o')
plt.plot(X,Y)
plt.subplot(1,2,2)
plt.plot(X,Y-Ye);
## END SOLUTION
../../../_images/881b9025883de0a51face8a77dac2361596acf28135a731067475b306fb08db1.png

9.1.3.6. Analyse de l’erreur#

Analyser cette interpolation et son évolution en fonction de Ne.

  • écrire une fonction erreurP2(F,L,ne) qui calcule la norme (norme du max) de l’erreur d’interpolation entre une fonction F(x) et son interpolation sur ne elements P2.

  • étudier l’évolution de cette erreur d’interpolation en fonction de Ne.

  • en déduire la précision (on pourra utiliser polyfit de numpy)

def erreurP2(F,L,ne):
    '''calcul erreur interpolation (norme du max) de la fonction F sur [0,L] avec ne elts'''
    ## BEGIN SOLUTION
    Xp= np.linspace(0,L,ne+1)
    Yp= F(Xp)
    X = np.linspace(0,L,200)
    Y = [interpolP2(x,Yp,L) for x in X]
    Ye = F(X)
    Err=np.max(np.abs(Y-Ye))
    return Err
    ## END SOLUTION

# vérification
print("erreur Ne=4,8 ",erreurP2(f,L,4),erreurP2(f,L,8),"Gain:",erreurP2(f,L,4)/erreurP2(f,L,8))

erreur Ne=4,8  0.18189212393470489 0.022740822509053737 Gain: 7.998484833267957

'''test sur une fonction quadratique'''
Fl = lambda x:3*x*x+2*x+1
assert np.abs(erreurP2(Fl,L,4)) < 1.e-8
assert np.abs(erreurP2(Fl,L,8)) < 1.e-8
printmd("### Validation OK")

Validation OK

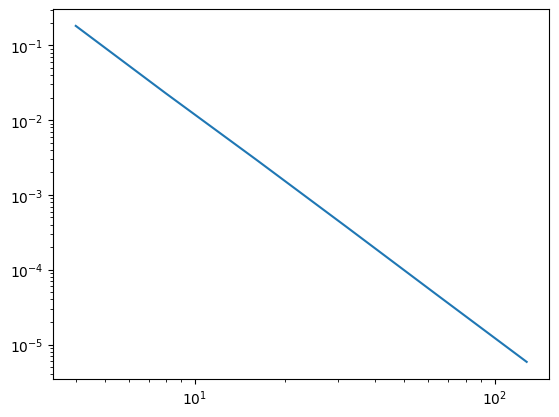
## BEGIN SOLUTION
NE=[4,8,16,32,64,128]
Err=np.zeros(len(NE))
for i,ne in enumerate(NE):
   Err[i]=erreurP2(f,L,ne)
#
plt.loglog(NE,Err)
pente= np.round(np.polyfit(np.log(NE),np.log(Err),deg=1)[0],2)
print("ordre ",-pente)
## END SOLUTION

ordre  2.98
../../../_images/b34c52c89e08e9593364caac26899f03b2abe605ede02a1f300cf8f783937060.png

9.1.3.7. Commentaires#

ecrire vos commentaires et anamyse(2 pts)

=== BEGIN ANSWER ===

=== END ANSWER ===

9.1.4. FIN#

Contenu