2.1. Modélisation de l’effet Magnus

2.1.1. Introduction

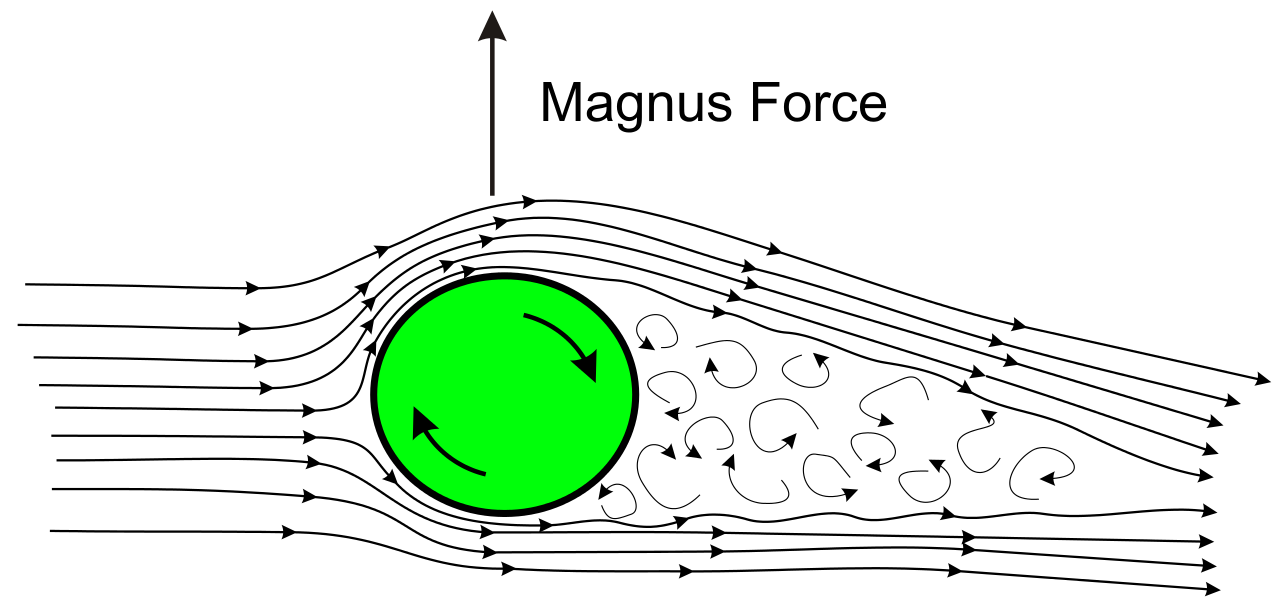
Effet Magnus (wikipedia)

: L’effet Magnus, découvert par Heinrich Gustav Magnus (1802-1870), physicien allemand, est un principe physique qui explique la force tangentielle subie par un objet en rotation se déplaçant dans un fluide. C’est cette force qui explique la modification de trajectoire d’une balle de tennis ou un ballon de football lifté . Cet effet est également utilisé comme moyen de sustentation ou de propulsion.

2.1.1.1. Principe

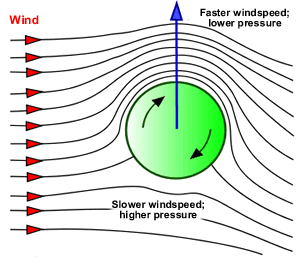
Le cylindre en rotation dans l’écoulement de fluide incompressible ci-dessous va accélérer le fluide en dessus du cylindre (car la vitesse de rotation du cylindre s’ajoute à celle du fluide), alors qu’il décélère le fluide en dessous (car la vitesse de rotation du cylindre est opposée à celle du fluide).

En négligeant la dissipation visqueuse, et en utilisant la relation de Bernoulli, cette variation de vitesse induit une dépression en dessus du cylindre et une surpression en dessous, d’où l’apparition une force perpendiculaire à l’écoulement et dirigée vers le haut.

2.1.1.2. Application: Propulsion de navire

Flettner rotor ship (1920) par Anton Flettner (aérodynamicien allemand)

E-ship (2010) transport de pales de turbine (Enercon GmbH.)

2.1.2. Analyse dimensionnelle

5 paramètres:

: \(\rho\) \(U_{0}\) \(R\) \(\omega\) et \(F_{p}\) (force de portance)

3 unités:

: \(m\) , \(s\) , \(kg\)

2 nombres sans dimension:

\[C_{p}=\frac{F_{p}}{\rho U_{0}^{2} R}\mbox{ et }\alpha=\frac{\omega R}{U_{0}}\]

Forme sans dimension de la loi de portance (effet magnus)

\[C_{p}=f(\alpha)\]

2.1.3. Définition du problème

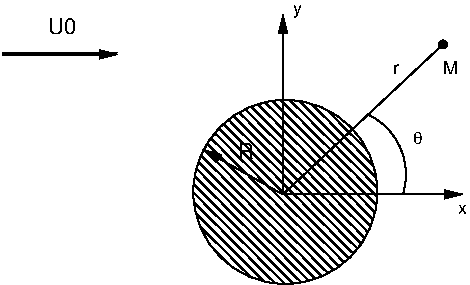
On considère l’écoulement d’un fluide incompressible (air à des faibles vitesses d’écoulement), de masse volumique \(\rho\) constante, autour d’un obstacle cylindrique de rayon R et d’axe Oz.

L’écoulement est à deux dimensions (vitesses parallèles au plan xOy et indépendantes de z) et stationnaire. Un point M du plan xOy est repéré par ses coordonnées polaires \((r,\theta)\). L’obstacle, dans son voisinage, déforme les lignes de courant ; loin de l’obstacle, le fluide est animé d’une vitesse uniforme \(U_{0}\) suivant Ox.

{width= »60% »}

L’écoulement est supposé irrotationnel, et le fluide est supposé parfait (viscosité nulle).

Dans ce cas l’écoulement est un écoulement potentiel, c.a.d que la vitesse découle d’un champ potentiel \(\Phi(x,y)\):

\[\begin{split}\overrightarrow{U}=\overrightarrow{grad}\,\Phi=\left[\begin{array}{c} \frac{\partial\Phi}{\partial x}\\ \frac{\partial\Phi}{\partial y} \end{array}\right]\end{split}\]

qui vérifie une équation de Laplace:

\[\Delta\Phi=\frac{\partial^{2}\Phi}{\partial x^{2}}+\frac{\partial^{2}\Phi}{\partial y^{2}}=0\]

Les conditions aux limites sont telles que loin de l’obstacle la vitesse est égale à \(U_{0}\), et que le fluide glisse sur l’obstacle, c.a.d. que la vitesse normale est nulle \(\overrightarrow{U}.\overrightarrow{n}=0\).

2.1.3.1. Solution analytique

La solution analytique de ce problème peut être calculée avec la théorie des fonctions conformes (champ uniforme plus dipôle):

\[\Phi=U_{0}(\frac{R^{2}}{r}+r)\cos\theta\]

Cette solution est tracée sur la figure ci-dessous. Le champ de vitesse est perpendiculaire aux lignes de potentiel ( \(\overrightarrow{U}\) est parallèle à \(\overrightarrow{grad}\Psi\) ). Sur le cercle \((r=R)\), la vitesse normale est nulle \((\frac{\partial\Phi}{\partial r}=0)\) et la vitesse tangentielle vaut:

\[U_{\theta}=\frac{1}{r}\frac{\partial\Phi}{\partial\theta}=-2U_{0}\sin\theta\]

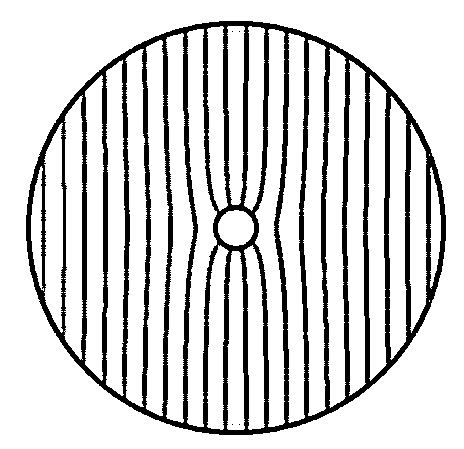
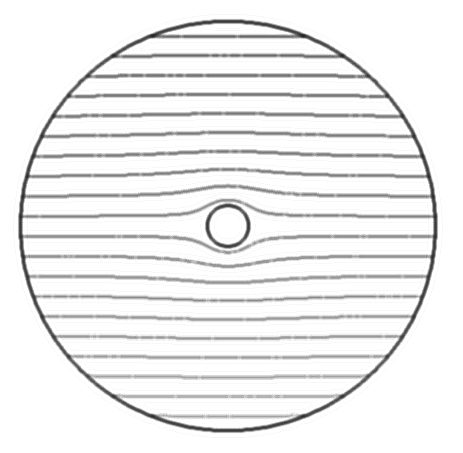
Cette fonction potentielle \(\Phi\) est associée à une fonction orthogonale \(\Psi\) (tracée ci-dessus), telle que

\[\begin{split}\overrightarrow{U}=\left[\begin{array}{c} \,\frac{\partial\Psi}{\partial y}\\ -\frac{\partial\Psi}{\partial x} \end{array}\right]\end{split}\]

Cette fonction \(\Psi\) est la fonction de courant de l’écoulement, i.e. les lignes \(\Psi=cste\) sont des lignes tangentes au vecteur vitesse ( \(\overrightarrow{U}.\overrightarrow{grad}\,\Psi=0\)). L’écoulement étant stationnaire, ces lignes correspondent aux trajectoires des particules fluides. On montre facilement que \(\Psi\) vérifie aussi une équation de Laplace:

\[\Delta\Psi=0\]

Les conditions aux limites associées sont:

(2.1)\[\Psi(r=\infty)=yU_{0}\,\,,\,\,\,\Psi(r=R)=0\]

2.1.3.2. Simulation par éléments finis

Pour résoudre ce problème par élément finis, on choisit un domaine de calcul \(\Omega\) fini: i.e. la frontière \(r=\infty\) est ramenée à une distance finie \(r=10R\) du cylindre (à cette distance la perturbation due au cylindre est négligeable): \(\Omega=[R,10R]x[0,2\pi]\). On note \(\Gamma_{0}(r=10R)\) la frontière extérieure et \(\Gamma_{1}(r=R)\) la frontière du cylindre.

On découpe le domaine \(\Omega\) en \(N_{e}\) éléments triangulaires (triangulation):

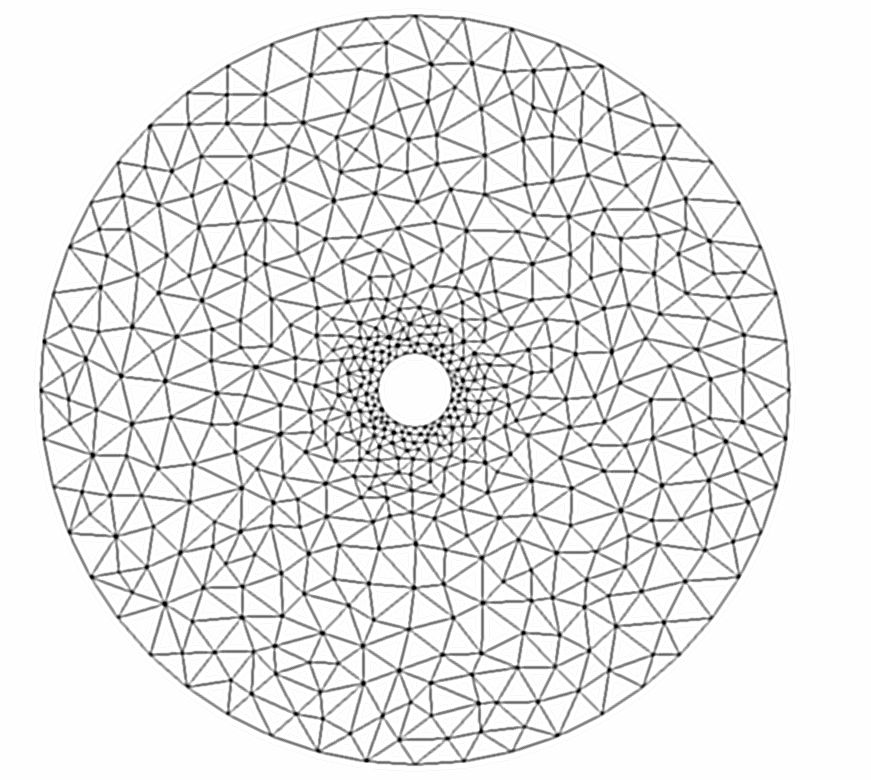
A partir de ce maillage, on construit ensuite une solution approchée \(\Psi^{h}(x,y)\) comme une approximation polynomiale par morceaux. Ainsi avec une approximation quadratique (élément finis \(P^{2}\)), sur chaque élément \(e_{k}\), la solution est un polynôme de degré 2 en x et y:

\[\Psi^{h}(x,y)=a_{0}+a_{1}x+a_{2}y+a_{3}xy+a_{4}x^{2}+a_{5}x^{6}\]

et possède donc 6 degrés de liberté, qui sont les 3 valeurs aux sommets de l’élément et les 3 valeurs sur les milieux de cotés

Compte tenu des conditions aux limites et de la continuité inter-éléments, la solution \(\Psi^{h}\) possède \(N\) degrés de liberté (ce nombre dépend du nombre d’éléments et du nombre de noeuds sur les frontières) et s’écrit:

\[\Psi^{h}(x,y)=\sum_{j=1}^{N}\Psi_{j}\phi_{j}(x,y)+\sum_{k\in\Gamma_{0}\cup\Gamma_{1}}\Psi_{0}\Phi_{k}(x,y)\]

Le terme en \(\Psi_{0}\) permet de vérifier les conditions aux limites:

\[\Psi_{0}|_{\Gamma_{0}}=U_{0}y\,\,,\,\,\Psi_{0}|_{\Gamma_{1}}=0\]

Pour déterminer les valeurs inconnues \(\Psi_{j}\), on écrit la formulation faible de la méthode des résidues pondérés, en multipliant l’équation [(2.1)] par une fonction test \(w_{i}(x,y)\), puis en intégrant sur le domaine \(\Omega\):

\[\int_{\Omega}\Delta\Psi^{h}\,w_{i}\,dxdy=0\]

On intègre par partie, en utilisant la formule de Green, pour obtenir la relation suivante:

\[\int_{\Omega}\overrightarrow{grad}\Psi^{h}.\overrightarrow{grad}w_{i}\,d\Omega-\int_{\Gamma}\overrightarrow{grad}\Psi^{h}.\overrightarrow{n}\,w_{i}\,d\Gamma=0\]

En utilisant la méthode de Galerkin, les fonctions tests \(w_{i}\) sont les fonctions de base \(\phi_{i}\) associées au degré de liberté de \(\Psi^{h}\):

\[w_{i}(x,y)=\frac{\partial\Psi^{h}}{\partial\Psi_{i}}=\phi_{i}(x,y)\]

Ces fonctions tests s’annulent sur la frontière \(\Gamma\) de \(\Omega\), et donc l’intégrale de bord sur \(\Gamma\) est nulle. En remplaçant \(\Psi^{h}\) par son expression éléments finis, la formulation faible s’écrit:

\[\sum_{j=1}^{N}\Psi_{j}\int_{\Omega}\overrightarrow{grad}\phi_{j}.\overrightarrow{grad}\Phi_{i}\,d\Omega=-\sum_{k\in\Gamma_{1}}\Psi_{0}\int_{\Omega}\overrightarrow{grad}\phi_{k}.\overrightarrow{grad}\Phi_{i}\,d\Omega\,\,\,\forall i=1,N\]

qui est un système linéaire de \(N\) équations pour \(N\) inconnues \(\{\Psi_{j}\}_{j=1,N}\) qu’il suffit de résoudre pour obtenir la solution approchée \(\Psi^{h}\).

2.1.3.3. Résolution avec COMSOL

COMSOL est un programme qui permet de calculer l’approximation par éléments finis d’un problème physique. Les différentes étapes de la résolution sont:

1. choix du modèle physique (EDP) et choix du degré d’approximation (éléments \(P^{2}\) par défaut).

2. création de la géométrie

3. définition des coefficients du modèle dans \(\Omega\)

4. définition des conditions aux limites sur la frontière \(\Gamma=\partial\Omega\)

5. maillage du domaine de calcul

6. résolution

7. analyse et tracé de la solution

2.1.3.4. Validation du résultat numérique

La solution analytique de ce problème s’écrit:

\[\Psi_{e}(x,y)=U_{0}r\,\sin\theta\,(1-\frac{R^{2}}{r^{2}})\]

On peut alors calculer l’erreur entre cette solution exacte et la solution par élément finis, et on trouve

\[-9.3\,10^{-3}\leq\Psi_{e}-\Psi^{h}\leq9.3\,10^{-3}\,\,\,\mbox{avec}\,\,\,\left|\psi_{e}\right|\leq0.93\]

En analysant cette erreur, on peut s’apercevoir qu’une partie de l’erreur est due à la condition aux limites sur \(\Gamma_{1}\), car avec les conditions aux limites imposées on a \(\Psi^{h}\neq\Psi_{e}\) sur \(\Gamma_{1}\). En imposant exactement sur \(\Gamma_{1}\)\(\Psi^{h}=\Psi_{e}\), on obtiens une erreur encore beaucoup plus faible:

\[-1.24\,10^{-4}\leq\Psi_{e}-\Psi^{h}\leq9.5\,10^{-5}\]

Attention

: sensibilité de la solution numérique aux conditions aux limites à l’infini

2.1.4. Application: étude de l’effet Magnus

2.1.4.1. Description du modèle

On reprend l’exemple précédent, en supposant que le cylindre tourne à vitesse angulaire \(\omega_{0}\overrightarrow{e}_{z}\). On suppose maintenant que le fluide est visqueux, pour pouvoir être entraîné par le cylindre, mais reste irrotationnel. L’écoulement reste un écoulement à potentiel, vérifiant une équation de Laplace:

\[\Delta\Psi=0\]

Les conditions aux limites sont telles que loin de l’obstacle la vitesse est égale à \(U_{0}\). Pour la condition aux limites sur l’obstacle, la condition physique est que la vitesse du fluide doit être égale à la vitesse du cylindre \(U_{r}=\omega_{0}R\), Cependant, cette condition aux limites n’est pas compatible avec les hypothèses de fluide irotationnel. On impose donc une condition moins forte: l’égalité de l’intégrale de la vitesse tangentielle sur le cylindre, et la condition d’imperméabilité, soit

\[\oint_{r=R}\overrightarrow{U}.\overrightarrow{dl}=2\pi\omega_{0}R^{2},\,\,\,\,\overrightarrow{U}.\overrightarrow{n}=0\]

La première condition impose la circulation de vitesse \(\kappa\) autour du cylindre:

\[\kappa=\oint_{r=R}\overrightarrow{U}.\overrightarrow{dl}=\int_{0}^{2\pi}u_{\theta}(R,\theta)\,d\theta=2\pi\omega_{0}R^{2}\]

qui peut s’interpréter comme la condition qu’en moyenne la vitesse du fluide \(u_{\theta}\) sur le cylindre est égale à la vitesse du cylindre \(\omega_{0}R\).

La mise en rotation du fluide par le cylindre engendre autour du cylindre une répartition de pression qui n’est plus symétrique par rapport à \(Ox\). Cette répartition de pression crée une force de portance sur le cylindre \(\Gamma_{1}\) (suivant Oy):

\[F=\int_{\Gamma_{1}}p\,n_{y}ds\]

où \(n_{y}\) est la composante suivant y de la normale \(\overrightarrow{n}\) à la surface \(\Gamma\). La théorie des écoulements potentiels montre que cette force est proportionnelle à la circulation \(\kappa\)

\[F=-\rho_{0}U_{0}\kappa\]

Cette force de portance, perpendiculaire à la vitesse du fluide loin du cylindre, est appelée effet Magnus et explique les mouvements de lift des balles de tennis ou de golf.

2.1.4.2. Mise en équation

Pour résoudre ce problème par éléments finis, on calcule une approximation \(\Psi^{h}\) de la fonction de courant \(\Psi\) solution de:

\[\Delta\Psi=0\,\,\mbox{\,\,\ dans\,}\,\Omega\]

associée aux conditions aux limites:

\[\Psi|_{\Gamma_{0}}=U_{0}y,\,\,\,\Psi|_{\Gamma_{1}}=\Psi_{1}\]

La seconde conditions aux limites implique que le cylindre \(\Gamma_{1}\) est une ligne de courant et la valeur \(\Psi_{1}\neq0\) imposée est telle que l’on ait une circulation \(\kappa\) autour du cylindre.

2.1.4.2.1. solution sans rotation

\[\Delta\Psi_{1}=0\,\,\mbox{\,\,\ dans\,}\,\Omega\]

associée aux conditions aux limites:

\[\Psi_{1}|_{\Gamma_{0}}=U_{0}y,\,\,\,\Psi_{1}|_{\Gamma_{1}}=0\]

2.1.4.2.2. solution avec rotation pure

\[\Delta\Psi_{2}=0\,\,\mbox{\,\,\ dans\,}\,\Omega\]

associée aux conditions aux limites:

\[\Psi_{2}|_{\Gamma_{0}}=0,\,\,\,\Psi_{2}|_{\Gamma_{1}}=1\]

2.1.4.2.3. solution générale

c’est une combinaison linéaire des 2 solutions de base

\[\psi=\psi_{1}+\beta\psi_{2}\]

Pour déterminer \(\beta\), il faut une condition supplémentaire. Dans notre cas on va imposer la position du point d’arrêt \(P_{a}\) sur le cylindre, ce qui va fixer \(\beta\). En effet par définition, la vitesse doit être nulle au point d’arrêt \(P_{a}\). Hors \(P_{a}\) est sur le cylindre, donc sa vitesse normale est nulle (imperméabilité). La condition impose donc la nullité de la vitesse tangentielle en \(P_{a}\):

\[\overrightarrow{U}(P_{a}).\overrightarrow{t}=0\]

En notant \(\theta_{a}\) l’angle du point d’arrêt \(P_{a}=[R\cos\theta_{a},R\sin\theta_{a}]\), la condition s’écrit en fonction de \(\psi\):

\[-\frac{\partial\psi}{\partial y}\sin\theta_{a}-\frac{\partial\psi}{\partial x}\cos\theta_{a}=0\]

ce qui fournit la relation pour calculer \(\beta\):

\[\frac{\partial\psi_{1}}{\partial y}\sin\theta_{a}+\frac{\partial\psi_{1}}{\partial x}\cos\theta_{a}=\beta\left(\frac{\partial\psi_{2}}{\partial y}\sin\theta_{a}+\frac{\partial\psi_{2}}{\partial x}\cos\theta_{a}\right)\]

2.1.4.3. Résolution avec COMSOL

Les différentes étapes de la résolution sont:

1. choix du modèle physique (EDP) et choix du degré d’approximation (éléments \(P^{2}\) par défaut).

2. création de la géométrie

3. maillage du domaine de calcul

4. définition des coefficients du modèle dans \(\Omega\)

5. définition des conditions aux limites sur la frontière \(\Gamma=\partial\Omega\)

6. résolution

7. analyse et tracé de la solution

Un exemple de résultat de simulation de l’effet Magnus avec Comsol est accessible sous le lien suivant

• Simulation de l’effet Magnus avec COMSOL

2.1.4.4. Analyse du résultat

Pour analyser le résultat, on calcule tout d’abord le champ de pression en utilisant Bernoulli:

\[p+\frac{1}{2}\rho u^{2}=cste\]

soit en fonction de \(\Psi\) (à une constante près)

\[p=-\frac{1}{2}\rho(\left(\frac{\partial\Psi}{\partial x}\right)^{2}+\left(\frac{\partial\Psi}{\partial x}\right)^{2})\]

On en déduit la force de portance \(F\)

\[F=\int_{\Gamma_{1}}p.n_{y}\,d\Gamma\]

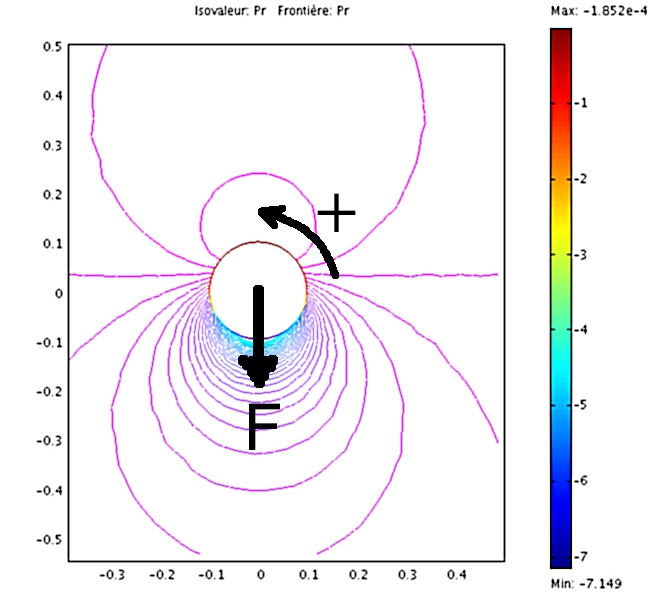
Avec COMSOL, on obtiens pour \(\Psi_{0}=0.4\), \(U_{0}=1\), \(\rho_{0}=1\) et \(R=0.1\) :

\[F=-1.098\]

Le calcul de la circulation \(\kappa\) en fonction de \(\Psi\) s’écrit:

\[\kappa=\int_{\Gamma_{1}}\left(\frac{\partial\Psi}{\partial x}n_{x}+\frac{\partial\Psi}{\partial y}n_{y}\right)d\Gamma\]

puisque \(u_{\theta}=\overrightarrow{U}.\overrightarrow{t}=\frac{\partial\Psi}{\partial x}n_{x}+\frac{\partial\Psi}{\partial y}n_{y}\).

Le calcul COMSOL donne:

\[\kappa=1.090\]

ce qui est en très bon accord avec la théorie (solution exacte), qui pour une circulation positive, prédit une force de portance négative. Compte tenu de cette relation, on peut aussi en déduire la vitesse de rotation \(\omega_{0}\) du cylindre pour la valeur de \(\Psi_{1}\) imposée:

\[\omega_{0}=17.34\,rd/s\]

2.1.5. Précision d’une simulation numérique

La précision d’un calcul numérique dépend de plusieurs facteurs, parmi lesquels:

1. le modèle mathématique

2. la discrétisation numérique du modèle mathématique

3. la précision des calculs sur l’ordinateur

Le dernier point est en général négligeable si on prend le soin de faire des calculs en double précision.

L’erreur due au choix du modèle mathématique dépend évidemment du problème physique.

L’erreur de discrétisation dépend du choix de la méthode numérique utilisée. Dans la cas des éléments finis, elle dépend:

1. du choix de l’interpolation : \(P^{1}\), \(P^{2}\) …

2. du choix et de la qualité du maillage \(\mathcal{T}^{h}\)

3. de la façon d’imposer les conditions aux limites

Pour des éléments finis, l’erreur de discrétisation est en général majorée par une erreur d’interpolation, qui pour une approximation \(P^{q}\) est d’ordre \(\theta(h^{1+q})\), où \(h\) est la dimension caractéristique de l’élément.

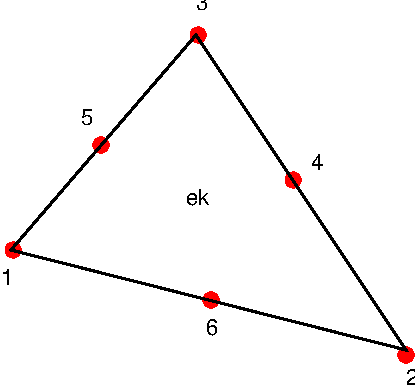
Pour un triangle \(e_{k}\), on définit la taille \(h_{k}\) comme la longueur du plus grand coté (figure ci-dessous).

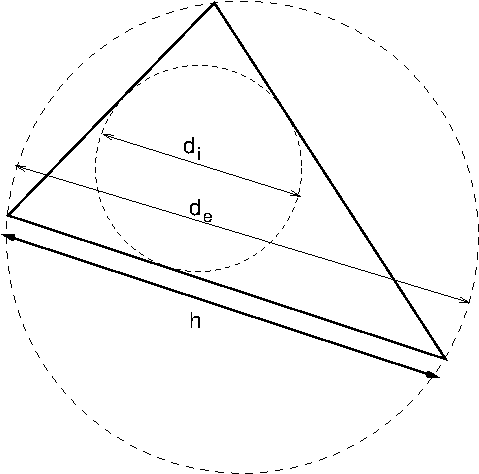
On définit aussi le diamètre \(d_{i}\) du cercle inscrit et le diamètre \(d_{e}\) du cercle circonscrit, ainsi que le rapport d’aspect du triangle \(R=\frac{d_{i}}{d_{e}}\). Pour un triangle équilatéral, on a \(d_{e}=h\) et \(d_{i}=\frac{\sqrt{2}}{3}h\), donc \(R=\frac{\sqrt{2}}{3}\). Par contre pour un triangle de plus en plus aplati, le rapport d’aspect tend vers 0 (car \(d_{i}\rightarrow0\)) , ce qui indique la dégénérescence du triangle.

Avec ces définitions, on montre que l’erreur d’interpolation \(\mathcal{P}^{1}\) sur un triangle vérifie une relation du type:

\[\left\Vert f-f^{h}\right\Vert =\sqrt{\int_{e_{k}}(f-f^{h})^{2}\,dxdy}\,\le\,C\,h_{k}^{2}\,\sqrt{\int_{e_{k}}\left((\frac{\partial^{2}f}{\partial x^{2}})^{2}+(\frac{\partial^{2}f}{\partial y^{2}})^{2}\right)dxdy}\]

Cependant la constante \(C\) dépend du rapport d’aspect \(R\) et l’estimation d’erreur dégénère lorsque \(R\rightarrow0\), i.e. lorsque le triangle devient de plus en plus aplatis.

Sous COMSOL, la qualité du maillage permet d’avoir une idée sur la valeur de ce rapport d’aspect \(R\). Pour cela, on calcul sur chaque élément la valeur suivante, fonction de l’aire \(A\) et de la longueur des cotés \(h_{1},h_{2},h_{3}\):

\[q=\frac{4\sqrt{3}A}{h_{1}^{2}+h_{2}^{2}+h_{3}^{2}}\]

qui varie de 0 (si le triangle est dégénérée) à 1 (pour un triangle équilatéral \(h_{1}=h_{2}=h_{3}=h\) et \(A=\frac{\sqrt{3}}{4}h^{2}\)). Un bon maillage nécessite en générale une valeur \(q\ge0,3\).