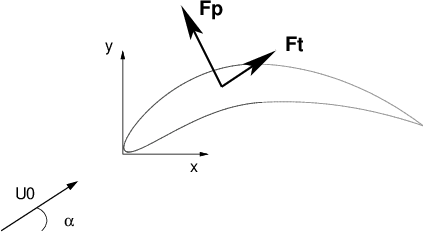
Ecoulement autour d’un profil NACA

Contenu

3.4. Ecoulement autour d’un profil NACA#

profil naca

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt

3.4.1. Définition d’un profil NACA#

Un profil NACA est un profil d’aile standardisé défini à partir de 3 paramètres:

l’épaisseur relative $t$
la cambrure relative $y_{a}$ au point $x_{a}$ de la ligne moyenne

3.4.1.1. profil Naca symétrique#

Dans ce cas $y_{a} = x_{a} = 0$ et le seul paramètre est l’épaisseur relative $t$ . L’extrados est donné par la courbe $y_{e} == F (x)$ suivante et l’intrados par la courbe symétrique $y_{i} = - F (x)$

F (x) = 5.0 t (0.2969 \sqrt{x} - 0.1260 x - 0.3516 x^{2} + 0.2843 x^{3} - 0.1036 x^{4}) pour 0 \leq x \leq L_{c}

La longueur de la corde $L_{c}$ suivant x est donnée par la racine de $F (L_{c}) = 0$ , i.e. $L_{c} = 1$ (sans dimension)

Un profil NACA symétrique à 4 chiffres est donnée par la nomenclature NACA00yz où les 2 chiffres yz représente l’épaisseur relative du profil $t = y z / 100$ .

3.4.1.2. profil cambré Naca à 4 chiffres#

Dans ce cas on donne la ligne moyenne du profil en fonction de $x_{a}$ et $y_{a}$ . Cette ligne moyenne a pour équation en fonction de x

\begin{array}{r} y_{m} = {\begin{cases} \frac{y_{a} (2 x_{a} - x) x}{x_{a}^{2}} si 0 \leq x \leq x_{a} \\ \frac{y_{a} (1 - x) (1 + x - 2 x_{a})}{(1 - x_{a})^{2}} si x_{a} \leq x \leq L_{c} \end{cases} \end{array}

L’équation de l’extrados $y_{e}, x_{e}$ est obtenu à partir de cette ligne moyenne, en introduisant l’angle $θ$

θ (x) = \frac{d y_{m}}{d x}

et la fonction F(x)précédente:

x_{e} (x) = x - F (x) \sin (θ (x))

y_{e} (x) = y_{m} + F (x) \cos (θ (x)) pour 0 \leq x \leq L_{c}

L’équation de l’intrados $x_{i}, y_{i}$ correspond à l’équation symétrique en y

x_{i} (x) = x + F (x) \sin (θ (x))

y_{i} (x) = y_{m} - F (x) \cos (θ (x)) pour 0 \leq x \leq L_{c}

La longueur de la corde $L_{c}$ vérifie $y_{e} (L_{c}) = y_{i} (L_{c})$

Un profil NACA cambré à 4 chiffres est donnée par la nomenclature NACAwxyz où les 2 chiffres yz représentent l’épaisseur relative du profil ( $t = y z / 100$ ), le chiffre w la courbure relative en % ( $y_{a} = w / 100$ ) et le chiffre x la position de la flèche de la ligne moyenne en 1/10 de corde ( $x_{a} = x / 10$ ).

3.4.1.3. profil cambré Naca à 5 chiffres#

Un profil NACA cambré à 5 chiffres est donnée par la nomenclature NACAabcyz où les 2 derniers chiffres yz représentent l’épaisseur relative du profil (t=yz/100), et abc vaut 210,220,230,240,250 pour des cambrure simples et 211,221,231,241,251 pour des cambrures doubles. Les équations sont les mêmes sauf pour l’équation de la ligne moyenne y_{m} que l’on la trouvera sur le site Wikipédia ici :

WIKIPEDIA

3.4.2. liste des profils étudiés#

fichier='listenaca.txt'
f = open(fichier,'r')
profils = f.readlines()
f.close()
# remove /n
profils = [p.strip() for p in profils]
print(profils)

3.4.3. Tracé de profils NACA#

def traceProfil(Ep,Xa,Ya):
    def F(x):
        return 5*Ep*(0.2969*np.sqrt(x)-0.1260*x-0.3537*x**2+0.2843*x**3-0.1015*x**4)
    def Ym(x):
        if (x<Xa): 
            return Ya*(2*Xa-x)*x/Xa**2
        else :
            return Ya*(1-x)*(1+x-2*Xa)/(1-Xa)**2
    def Theta(x):
        if (x<Xa): 
            return Ya*(2*Xa-x)/Xa**2-Ya*x/Xa**2
        else :
            return Ya*(1-x)/(1-Xa)**2-Ya*(1+x-2*Xa)/(1-Xa)**2
    #
    X = np.linspace(0,1,100)
    FX= np.zeros(X.size); THETA= np.zeros(X.size); YM= np.zeros(X.size);
    for i,x in enumerate(X):
        FX[i]=F(x);
        THETA[i]=Theta(x);
        YM[i]=Ym(x);
    # nbre de points
    n=len(X);
    XX=np.zeros((2*n-1));
    YY=np.zeros((2*n-1));
    ZZ=np.zeros((2*n-1));
    XX[:n]=X  - FX*np.sin(THETA);
    YY[:n]=YM + FX*np.cos(THETA);
    XX[n::]= X[n-2::-1]  + FX[n-2::-1]*np.sin(THETA[n-2::-1])
    YY[n::]= YM[n-2::-1] - FX[n-2::-1]*np.cos(THETA[n-2::-1])
    # tracer profil et ligne moyenne
    plt.plot(XX,YY,'-')
    plt.plot(X,YM,'--')
    return

3.4.3.1. Profil NACA wxyz#

Un profil NACA cambré à 4 chiffres est donnée par la nomenclature NACAwxyz où les 2 chiffres yz représentent l’épaisseur relative du profil ( $t = y z / 100$ ), le chiffre w la courbure relative en % $y_{a} = w / 100$ et le chiffre x la position de la flèche de la ligne moyenne en 1/10 de corde $x_{a} = x / 10$ .

$N A C A y_{a} x_{a} e_{p}$

# profil Naca4412 (xyee)
plt.figure(figsize=(12,6))
traceProfil(12./100,4./10,4./100.)
plt.title("Naca 4412")
plt.axis('equal');

# profil Naca2412 (xyee)
plt.figure(figsize=(12,6))
traceProfil(12./100,4./10,2./100.)
plt.title("Naca 2412")
plt.axis('equal');

3.4.4. Simulation avec XFOIL naca0012#

from xfoil import XFoil
xf = XFoil()

from xfoil.test import naca0012
xf.airfoil = naca0012

# naca 0012 xfoil
X = xf.airfoil.coords[:,0]
Y = xf.airfoil.coords[:,1]
# data COMSOL
X1,Y1 = np.loadtxt('Naca0012.txt',unpack=True)

plt.plot(X,Y,label="Comsol")
plt.plot(X1,Y1,'--',label="XFoil")
plt.title("Naca 0012")
plt.legend()
plt.axis('equal');

3.4.5. Lecture des résultats de simulation COMSOL#

from sol_naca import Naca,lecture,lecture_vitesse, portance
naca12 = lecture("PressionNaca0012.dat",12,0,0)
Fp = portance(naca12)
for num in range(0,naca12.alpha.size,2):
    plt.plot(naca12.X,naca12.Pr[:,num],label="$\\alpha$={:.1f}".format(np.degrees(naca12.alpha[num])))
plt.legend()
plt.xlabel("$x/L_c$")
plt.ylabel("$(p-p_0)/E_0$")
plt.title("Répartition de pression (calcul COMSOL)");

# solution pour un angle donnee
num=3
alpha = naca12.alpha[num]
Alpha = np.degrees(alpha)
# Xfoil
Cl, Cd, Cm, Cp = xf.a(Alpha)
# polaire: pression adim
Xp,Pr = xf.get_cp_distribution()
Pr = Pr*0.5
print("Cp Portance à alpha={:.1f}° COMSOL={:.3f} Xfoil={:.3f}".format(Alpha,Fp[num]/0.5,Cl))

plt.plot(naca12.X,naca12.Pr[:,num],label="COMSOL $\\alpha$={:.1f}".format(Alpha))
plt.plot(Xp,Pr,label="xfoil")
plt.title("Repartition pression")
plt.legend();

Cl,Cd,Cd,Cm,Cp,alpha

xref=0.25; yref=0.0
CL =  (np.trapz(naca12.Pr[:,num],naca12.X)*np.cos(alpha)   + np.trapz(naca12.Pr[:,num],naca12.Y)*np.sin(alpha))/0.5
CM = -(np.trapz(naca12.Pr[:,num]*(naca12.X-xref),naca12.X) + np.trapz(naca12.Pr[:,num]*(naca12.Y-yref),naca12.Y))/0.5
print(CM," ecart centre de poussée / 1/4 corde =",CM/CL)

Par définition le coefficiant de moment = moment des forces de pression / à P = xref=0.25,yref=0.0 (i.e. 1/4 cordre)

C m = \int p \vec{n} \land \vec{M P} d s = - \int p ((x - x_{r e f}) d x + (y - y_{r e f}) d y)

Donc le centre de poussée = 1/4 cordre / bord d’attaque est une bonne approximation (erreur 1/100)