4. Stucture de données

Marc BUFFAT, dpt mécanique, Université Claude Bernard Lyon 1

Mise à disposition selon les termes de la Licence Creative Commons
Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 2.0 France.

Table des matières

• 1  Structure simple
  • 1.1  Vecteurs, Matrices
  • 1.2  Liste d'objets non uniforme
  • 1.3  Dictionnaire
  • 1.4  Boucle sur les élèments
  • 1.5  boucle sur un dictionnaire
• 2  Exemple
• 3  Structure complexe
  • 3.1  Enregistrement (structure)
    • 3.1.1  structure avec définition explicite
    • 3.1.2  structure dynamique
• 4  TP: système solaire
  • 4.1  Définition d'une structure planete
  • 4.2  Tri
  • 4.3  Tracé du système solaire
    • 4.3.1  tracer des planetes
  • 4.4  Animation des planetes
• 5  Fin

%matplotlib inline
%autosave 300
import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
from matplotlib import rcParams
rcParams['font.family'] = 'serif'
rcParams['font.size'] = 14
from IPython.core.display import HTML
from IPython.display import display
from matplotlib import animation
#css_file = 'style.css'
#HTML(open(css_file, "r").read())

Autosaving every 300 seconds

4.1. Structure simple

4.1.1. Vecteurs, Matrices

tableau numpy

• accès avec un indice

• dimension fixe

• type uniforme

4.1.2. Liste d’objets non uniforme

liste python

• accès avec un indice

• dimension variable

• type différent

4.1.3. Dictionnaire

liste avec un indicage par mot clés - accès avec une clé (key) - dimension variable - type différent

4.1.4. Boucle sur les élèments

• par indice

• par valeur

• par indice et valeur

# boucle classique sur les indices
X = np.linspace(0.,1.,6)
for i in range(X.size):
    print("X[{}]={}".format(i,X[i]))

X[0]=0.0
X[1]=0.2
X[2]=0.4
X[3]=0.6000000000000001
X[4]=0.8
X[5]=1.0

# boucle sur les valeurs
for x in X:
    print("X[]=",x)

X[]= 0.0
X[]= 0.2
X[]= 0.4
X[]= 0.6000000000000001
X[]= 0.8
X[]= 1.0

# boucle sur les valeurs et indices
for i,x in enumerate(X):
    print("X[{}]={}".format(i,x))

X[0]=0.0
X[1]=0.2
X[2]=0.4
X[3]=0.6000000000000001
X[4]=0.8
X[5]=1.0

4.1.5. boucle sur un dictionnaire

• clé : valeur

• dico = { cle1:valeur1, cle2:valeur2, .. }

# dictionnaire
Dico={'mon':'my','personne':'nobody','nom':'name','est':'is'}
for mot in Dico:
    print("traduction de {} : {}".format(mot,Dico[mot]))

traduction de mon : my
traduction de personne : nobody
traduction de nom : name
traduction de est : is

# utilisation
phrase="mon nom est toto"
traduction=""
for mot in phrase.split():
    if mot in Dico:
        traduction += Dico[mot] + " "
    else:
        traduction += mot + " "
print(traduction)

my name is toto 

4.2. Exemple

on souhaite manipuler une liste d’étudiants avec leur nom (une chaine de caractère) et leur note (un nombre réel)

# version numpy
Noms  = np.array(['toto','bidule','machin'])
Notes = np.array([10.,16.0,13.])
print(Noms,Notes)
# recherche de la note d'un etudiant
etudiant='bidule'
for k in range(Noms.size):
    nom = Noms[k]
    if etudiant == nom :
        print("{} a pour note {}".format(nom,Notes[k]))

['toto' 'bidule' 'machin'] [10. 16. 13.]
bidule a pour note 16.0

# version avec liste
Listes = [['toto',10.],['bidule',16.],['machin',13.]]
print(Listes)
# recherche de la note d'un etudiant
nom='bidule'
for etudiant in Listes:
    if etudiant[0] == nom:
        print("{} a pour note {}".format(nom,etudiant[1]))

[['toto', 10.0], ['bidule', 16.0], ['machin', 13.0]]
bidule a pour note 16.0

# version avec dictionnaire
Etudiants = {'toto':10.,'bidule':16.,'machin':13.}
print(Etudiants)
# recherche de la note d'un etudiant
if nom in Etudiants:
    print("{} a pour note {}".format(nom,Etudiants[nom]))

{'toto': 10.0, 'bidule': 16.0, 'machin': 13.0}
bidule a pour note 16.0

4.3. Structure complexe

On veut représenter un élève qui est caractérisé son nom, son prénom, son numéro d’étudiant, sa moyenne générale, etc. On voudrait qu’une seule variable conserve et donc donne accès à toutes ces informations.

En algorithmique, on définirait alors un type enregistrement Eleve regroupant ces informations.

Le type Eleve contiens alors une chaîne de caratère (le nom), une deuxième chaîne de caractère (le prénom), un entier (numero étudiant), un réel (moyenne générale)

# representation avec des listes
eleve=['machin','chouette',123456,12.5]
print(eleve)
print("eleve numero:{} moyenne:{}".format(eleve[2],eleve[3]))

['machin', 'chouette', 123456, 12.5]
eleve numero:123456 moyenne:12.5

Problème

• accés aux données avec un indice (peu lisible)

• complexification

solution - accès avec un mot clé - eleve.nom - eleve.note

4.3.1. Enregistrement (structure)

Définition algorithmique : Un enregistrement est un type correspondant à un agrégat d’élément de types éventuellement différent auxquels on accède grâce à un nom.

en Python on peut l'implémenter avec la notion de classe

4.3.1.1. structure avec définition explicite

• à préférer !!!

# structure avec définition explicite
class Eleve():
    def __init__(self,name,forname,num,moy):
        self.nom     = name
        self.prenom  = forname
        self.numero  = num
        self.moyenne = moy
        return  

eleve = Eleve('machin','chouette',123456,12.5)
print("Eleve {} numero:{} moyenne:{}".
      format(eleve.nom,eleve.numero,eleve.moyenne))

Eleve machin numero:123456 moyenne:12.5

4.3.1.2. structure dynamique

• uniquement si nécéssaire !!!

• préférer une définition explicite

class Eleve():
    pass

eleve = Eleve()
eleve.nom    = 'machin'
eleve.prenom = 'chose'
eleve.numero = 123456
eleve.moyenne= 12.5
print("nom {} numero:{} moyenne:{}".
      format(eleve.nom,eleve.numero,eleve.moyenne))

nom machin numero:123456 moyenne:12.5

4.4. TP: système solaire

On veut manipuler les planétes du système solaire.

Une planéte est caractérisée par:

• son nom

• sa masse

• sa distance au soleil

• sa période de rotation

4.4.1. Définition d’une structure planete

# unite de masse : terre en kg
masse_terre = 5.9736e24 
class Planete():
    def __init__(self,name,dist,diametre,density,period):
        self.nom   = name
        self.masse = np.pi/6.*(density*1.e12)*\
                    diametre**3/masse_terre
        self.rayon = diametre/2.
        self.distance = dist
        self.periode  = period
        return

Terre = Planete("terre",150,12756,5.5,365.256)
Mars  = Planete("mars",228,6794,4.0,686.98)

# distance  terre/mars
dmin = -Terre.distance + Mars.distance
dmax =  Terre.distance + Mars.distance
print("distance terre mars: min {} max {} (10^6 km)".format(dmin,dmax))

distance terre mars: min 78 max 378 (10^6 km)

# durée du voyage (en jour) (vitesse du vaiseau en km/h)
V = 15000.0
tmin = (dmin*1e6/V)/24.
tmax = (dmax*1e6/V)/24.
print("duree min={:.2f}  max={:.2f} (jours)".format(tmin,tmax))

duree min=216.67  max=1050.00 (jours)

# fenetre de tir (periode alignement) en année
T = Terre.periode*Mars.periode/(Mars.periode-Terre.periode)/365.
print("periode fenetre de tir: {:.2f}a".format(T))

periode fenetre de tir: 2.14a

# liste de planetes
Jupiter=Planete("jupiter",778,143884,1.3,4332.6)
Venus  =Planete("venus",108,12104,5.3,224.701)
Saturne=Planete("saturne",1427,120536,0.7,10759.2)
SystemeSolaire=[Saturne,Terre,Mars,Jupiter,Venus]
#
def affiche(SSolaire):
    for planete in SSolaire:
        print("{:8s} masse {:6.2f} distance {:5.0f}mkm periode {:7.1f}j".format(
          planete.nom, planete.masse, planete.distance, 
          planete.periode))
    return
#
affiche(SystemeSolaire)

saturne  masse 107.45 distance  1427mkm periode 10759.2j
terre    masse   1.00 distance   150mkm periode   365.3j
mars     masse   0.11 distance   228mkm periode   687.0j
jupiter  masse 339.42 distance   778mkm periode  4332.6j
venus    masse   0.82 distance   108mkm periode   224.7j

4.4.2. Tri

tri bulle:

L’algorithme parcourt le tableau et compare les éléments consécutifs. Lorsque deux éléments consécutifs ne sont pas dans l’ordre, ils sont échangés.

Après un premier parcours complet du tableau du dernier au premier, le plus grand élément est forcément en fin de tableau, à sa position définitive.

tri_à_bulles(Tableau T)
   "n=nbre d'elements à trier"
   pour n allant de taille(T) - 1 à 1
      pour j allant de 0 à n - 1
       si T[j+1] < T[j]
           échanger(T[j+1], T[j])

N = len(SystemeSolaire)
for i in range(N):
    n = N-i  # nbre d'elements à trier    
    for j in range(n-1):
        planete_j  = SystemeSolaire[j]
        planete_j1 = SystemeSolaire[j+1]
        if planete_j1.distance < planete_j.distance:
            # echange des planetes dans le tableau
            SystemeSolaire[j]  = planete_j1
            SystemeSolaire[j+1]= planete_j
# affiche les planetes
affiche(SystemeSolaire)

venus    masse   0.82 distance   108mkm periode   224.7j
terre    masse   1.00 distance   150mkm periode   365.3j
mars     masse   0.11 distance   228mkm periode   687.0j
jupiter  masse 339.42 distance   778mkm periode  4332.6j
saturne  masse 107.45 distance  1427mkm periode 10759.2j

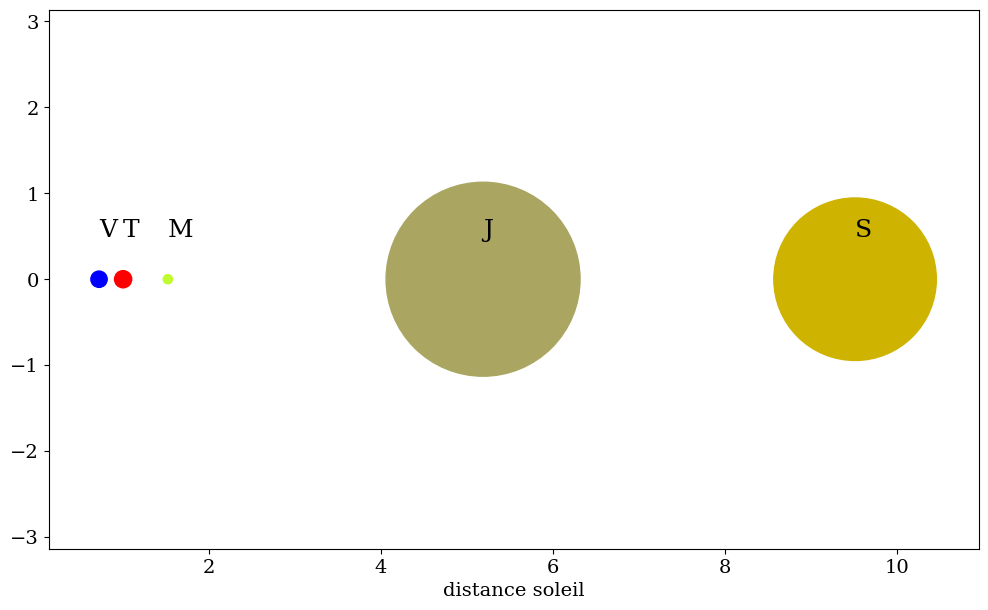
4.4.3. Tracé du système solaire

4.4.3.1. tracer des planetes

# adimensionnalisation
dist_terre  = Terre.distance
rayon_terre = Terre.rayon
# couleur des planetes
Couleurs=['b','r','#c0fb2d','#aaa662','#ceb301']
#
plt.figure(figsize=(12,7))
ax = plt.axes(xlim=(-10,10),ylim=(-5,5))
for k,planete in enumerate(SystemeSolaire):
    col= Couleurs[k]
    r1 = planete.distance/dist_terre
    r2 = 0.1*planete.rayon/rayon_terre
    c2 = plt.Circle((r1,0),radius=r2,color=col)
    ax.add_patch(c2)
    plt.text(r1,0.5,planete.nom[0].upper(),fontsize=18)
plt.axis('equal')
plt.xlabel('distance soleil')

Text(0.5, 0, 'distance soleil')

4.4.4. Animation des planetes

dist_terre  = Terre.distance
rayon_terre = Terre.rayon
Couleurs=['b','r','#c0fb2d','#aaa662','#ceb301']
Cplanetes=[0]*len(SystemeSolaire)
# figure
ax = None
fig = None
#
def init_anim():
    global SystemeSolaire, Cplanetes, fig, ax
    fig=plt.figure(figsize=(6,6))
    ax = plt.axes(xlim=(-10,10),ylim=(-10,10))
    r0 = 0.1
    c0 = plt.Circle((0,0),radius=r0,color='k')
    ax.add_artist(c0)
    for planete in SystemeSolaire:
        r1 = planete.distance/dist_terre
        c1 = plt.Circle((0,0),radius=r1,lw=1,fill=False)
        ax.add_patch(c1)
    plt.axis('equal')
    plt.axis('off')
    return
def init():
    global SystemeSolaire,Cplanetes,ax
    for k,planete in enumerate(SystemeSolaire):
        col= Couleurs[k]
        c2 = plt.Circle((0,0),radius=0,color=col)
        ax.add_patch(c2)
        Cplanetes[k]=c2
    return (Cplanetes[k] for k in range(len(SystemeSolaire)))
#
def animate(i):
    global SystemeSolaire,Cplanetes
    t  = i*20.
    for k,planete in enumerate(SystemeSolaire):
        r1 = planete.distance/dist_terre
        w1 = 2*np.pi/planete.periode
        r2 = 0.12*planete.rayon/rayon_terre
        x  = r1*np.cos(w1*t)
        y  = r1*np.sin(w1*t)
        Cplanetes[k].center = (x,y)
        Cplanetes[k].radius = r2
    return (Cplanetes[k] for k in range(len(SystemeSolaire)))
#

import matplotlib.animation as animation
from matplotlib import rc
init_anim()
anim=animation.FuncAnimation(fig, animate, range(200),interval=100, init_func=init)

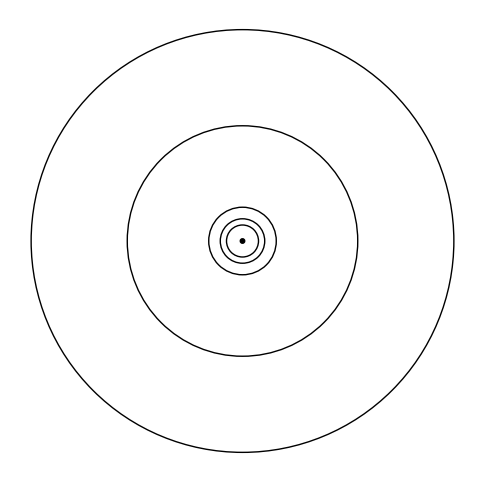
rc('animation', html='jshtml')
anim

Once Loop Reflect

4.5. Fin

print("\t\tSystème utilisé")
import sys
print("Système :\t\t",sys.platform)
import platform
print(platform.platform())
print("Ordinateur:\t\t",platform.machine())
print("Version de Python:\t",sys.version)
import IPython
print("Version de IPython:\t",IPython.__version__)
import numpy
print("Version de numpy:\t",numpy.version.version)
import scipy
print("Version de scipy:\t",scipy.version.version)
import matplotlib
print("Version de matplotlib:\t",matplotlib.__version__)

		Système utilisé
Système :		 linux
Linux-5.15.0-125-generic-x86_64-with-glibc2.35
Ordinateur:		 x86_64
Version de Python:	 3.10.12 (main, Feb  4 2025, 14:57:36) [GCC 11.4.0]
Version de IPython:	 8.26.0
Version de numpy:	 1.26.4
Version de scipy:	 1.15.2
Version de matplotlib:	 3.7.1