3.2. TP Écoulement autour d’un profil NACA avec COMSOL#
On considère l’écoulement potentiel autour d’un profil NACA en incidence (angle \(\alpha\)).
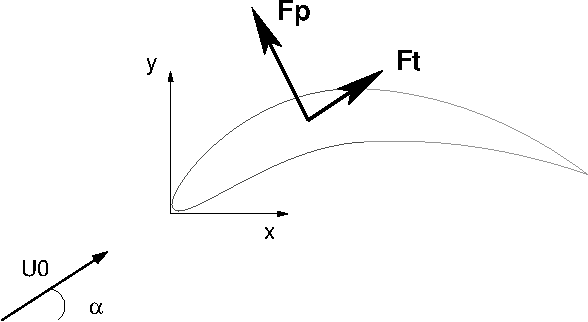
Pour effectuer la simulation sous COMSOL, il faut générer un maillage autour du profil. Pour cela on doit définir le profil NACA à l’aide d’un fichier de points au format DXF (CAO).
3.2.1. Définition d’un profil NACA#
Un profil NACA est un profil d’aile standardisé défini à partir de 3 paramètres:
l’épaisseur relative \(t\)
la cambrure relative \(y_{a}\) au point \(x_{a}\)de la ligne moyenne
3.2.1.1. profil symétrique#
Dans ce cas \(y_{a}=x_{a}=0\) et le seul paramètre est l’épaisseur relative \(t\). L’extrados est donné par la courbe sans dimension \(y_{e}==F(x)\) suivante et l’intrados par la courbe symétrique \(y_{i}=-F(x)\). Les longueurs sont adimensionalisées par la longueur de corde \(L_c\) du profil:
La fonction \(F(x)\) ne vérifie pas exactement \(F(1)=0\) et donc une épaisseur nulle au bord de fuite. Pour assurer une épaisseur nulle au bord de fuite pour la simulation numérique, on modifie le dernier coefficient par \(-0.1036\), ce qui induit un petit changement de la surface portante.
Un profil NACA symétrique à 4 chiffres est donnée par la nomenclature NACA00yz où les 2 chiffres \(yz\) représente l’épaisseur relative du profil \(t=yz/100\).
3.2.1.2. profil cambré Naca à 4 chiffres#
Dans ce cas on donne la ligne moyenne du profil en fonction de \(x_{a}\) et \(y_{a}\). Cette ligne moyenne a pour équation en fonction de \(x\)
L’équation de l’extrados \(\{y_{e},x_{e}\}\) est obtenu à partir de cette ligne moyenne, en introduisant l’angle \(\theta\)
et la fonction \(F(x)\)précédente:
L’équation de l’intrados \(\{x_{i},y_{i}\}\) correspond à l’équation symétrique en \(y\)
Un profil NACA cambré à 4 chiffres est donnée par la nomenclature NACAwxyz où les 2 chiffres \(yz\) représentent l’épaisseur relative du profil (\(t=yz/100\)), le chiffre \(w\) la courbure relative en % (\(y_{a}=w/100\)) et le chiffre \(x\) la position de la flèche de la ligne moyenne en \(1/10\) de corde (\(x_{a}=x/10\)).
3.2.1.3. profil cambré Naca 5 chiffres#
Un profil NACA cambré à 5 chiffres est donnée par la nomenclature NACAabcyz où les 2 derniers chiffres \(yz\) représentent l’épaisseur relative du profil (\(t=yz/100\)), et abc vaut 210,220,230,240,250 pour des cambrure simples et 211,221,231,241,251 pour des cambrures doubles. Les équations sont les mêmes sauf pour l’équation de la ligne moyenne \(y_{m}\) que l’on la trouvera sur le site Wikipédia ici :
3.2.2. Format CAO DXF#
DXF, sigle de Drawing eXchange Format, est un format créé par la société Autodesk servant à échanger des fichiers DAO ou CAO entre systèmes CAO n’utilisant pas le même format de fichier natif. Il a été conçu à l’origine pour représenter les modèles 3D créés avec AutoCAD.
Pour décrire une courbe, on la décrit par une liste de segments en donnant les coordonnées des 2 points extrémités et décrit dans le sens trigonométrique.
Dans l’exemple en annexe`, on décrit un triangle en définissant ces 3 cotés après les entêtes LINE et les codes 10,20,30 pour les coordonnes x,y,z du 1er point et 11,21,31 pour les coordonnées du 2nd point. Toutes les autres entêtes doivent être conservées.
# programme python pour l'écriture d'une courbe au format DXF dans un fichier
# la courbe est définie par les pts X,Y,Z
# attention si la courbe est fermée, le dernier pt = premier pt
def writedxf(nom,X,Y,Z):
fid=open(nom,'w')
fid.write('999\nCourbe au format DXF\n 0\nSECTION\n 2\nENTITIES\n 0\n')
for i in range(len(X)-1):
fid.write('LINE\n 8\n 0\n')
# ecriture du segment Pi-Pi+1
fid.write('10\n %.4f\n 20\n %.4f\n 30\n %.4f\n'%(X[i],Y[i],Z[i]))
fid.write('11\n %.4f\n 21\n %.4f\n 31\n %.4f\n'%(X[i+1],Y[i+1],Z[i+1]))
fid.write(' 0\n')
fid.write('ENDSEC\n 0\nEOF\n')
fid.close()
return
3.2.3. Simulations avec COMSOL#
L’objectif de l’étude est de simuler avec COMSOL l’écoulement autour du profil pour déterminer la force de portance et son point d’application pour différentes incidences \(-10^{\circ}\leq\alpha\leq20^{\circ}\).
En séance on traitera le cas d’un profil symétrique. Puis vous aurez à étudier le profil NACA qui vous a été attribué.
3.2.3.1. Préparation#
Pour effectuer la simulation avec COMSOL, il faut créer un fichier permettant de définir la géométrie du profil et mailler le domaine de calcul, et un second fichier pour extraire la répartition de pression sur le profil. Pour valider la simulation, on a aussi besoin de données de comparaison.
En utilisant le profil naca nacawxyz qui vous a été attribué, vous devez, en utilisant un programme python, créer 2 fichiers et donner la position du point J pour l’application de la condition de Kutta-Joukovsky.
Ecrire un fichier nacawxyz.dxf décrivant le profil avec un format CAO DXF (décrit en 2.2). On utilisera la fonction writedxf permettant d’écrire un fichier dxf qui vous est fournie et documentée en section 2.3. Nous considérerons ici des valeurs de Z nulles (étude 2D). Afin de décrire une courbe fermée, le dernier point du fichier devra être strictement équivalent au premier, et le premier point doit correspondre au bord de fuite.
Ecrire un fichier nacawxyz.txt contenant sur 2 colonnes les coordonnées des points sur le profil en partant du bord de fuite, avec un parcours dans le sens trigonométrique. Afin de décrire une courbe fermée, le dernier point du fichier devra être strictement équivalent au premier.
définir les coordonnée \(x_{j},x_{j}\) du point J où la condition de kutta-Jukowski doit être appliquée. Ce point doit se situer sur la tangente au bord de fuite. Il n’est numériquement pas possible d’appliquer cette condition exactement au bord de fuite. Le point J sera donc situé à une distance d du bord de fuite, tel que \(d<corde/20\). On donnera aussi les coordonnées de la tangente au bord de fuite.
Le site http://airfoiltools.com/ propose un référencement des caractéristiques aérodynamique de profil cambré. En utilisant leur moteur de recherche http://airfoiltools.com/search/index, recherchez le profil étudier. Grâce à l’onglet Airfoil detail, vous pouvez obtenir les caractéristiques (coeff traînée et portance en fonction de l’angle) pour différentes valeur du nombre de Reynolds. En choisissant une valeur de Re pertinente , extraire les valeur de \(C_{p}\) en fonction de l’angle \(\alpha\), que vous reporterez dans un fichier nacawxyz_portance.dat.
3.2.4. Bibliothèque d’analyse#
On va construire une bibliothèque d’analyse de la solution écrite en Python. On définit une structure de données Naca, correspondant à un profil naca d’épaisseur e, de point de cambrure (xa,ya), pour stocker N points X,Y (vecteurs numpy) sur le Naca (en partant du bord de fuite), les valeurs de la pression Pr (matrice numpy (N,nv) ) et de la vitesse (U, V) en ces N points fonction des nv valeurs alpha (vecteur numpy) de l’angle \(\alpha\) de la vitesse \(U_{0}\) par rapport à l’horizontal.
# donnees sur le NACA
class Naca():
def __init__(self,E,X0,Y0):
# caracteristique du profil (epaisseur, cambrure)
self.e = E
self.xa = X0
self.ya = Y0
# points sur le profil
self.X=None
self.Y=None
# donnees fct de l'angle d'incidence alpha
self.alpha=None
self.Pr=None
self.U =None
self.V =None
return
Écrire une fonction lecture(nom_fichier,E,Xa,Ya) qui lit les données de pression dans le fichier de nom nom_fichier pour un profil d’épaisseur E et de point de cambrure Xa,Ya, et qui renvoie une structure naca remplie. Pour l’extraction des valeurs de alpha stockées sur une ligne du fichier, on pourra utiliser la fonction read_alpha(line) fournie.
Écrire une fonction portance(naca) qui renvoie un vecteur numpy contenant la force de portance (par unité de longueur transverse) calculée avec les données de la structure naca pour toutes les valeurs de \(\alpha\). On pourra utiliser la fonction trapz de la bibliothèque numpy pour calculer les intégrales. On pourra calculer la portance en projettant la résultante de pression suivant x et y.
Écrire une fonction lecture_vitesse(nom_fichier,naca) qui lit les données de vitesse dans le fichier de nom nom_fichier et qui initialise la vitesse dans la structure naca. La fonction ne renvoie rien directement, mais modifie la structure naca (vitesse U et V).
Écrire une fonction circulation(naca) qui renvoie un vecteur numpy contenant la circulation de vitesse calculée avec les données de la structure naca pour toutes les valeurs de \(\alpha\). On pourra utiliser la fonction trapz de la bibliothèque numpy pour calculer les intégrales. On pourra calculer la circulation en décomposant \(\overrightarrow{U}.\overrightarrow{dl}\) suivant x et y.
On fournit un canevas python bib_naca.py.
3.2.5. Analyse des données#
En utilisant la bibliothèque précédente, écrire un programme python pour analyser les deux fichiers de résultats (pression et vitesse). Pour le profil naca étudié, on calculera l’angle \(\theta_{0}\) de la ligne moyenne au bord d’attaque et l’angle \(\theta_{1}\) de la ligne moyenne au bord de fuite. On calculera la portance et la circulation de vitesse en fonction de l’angle d’incidence \(\beta = \alpha-\theta_{0}\) par rapport à la ligne moyenne. Pour déterminer la précision des simulations, on calcule la vitesse au bord de fuite, et on définit l’erreur comme le rapport \(err=|un/ut|\) entre la vitesse normale \(un\) et la vitesse tangentielle \(ut\) au bord de fuite. On justifiera ce choix.
Une caractéristique importante d’un profil est la position du centre de pousée. C’est le point d’application de la résultante aérodynamique; il est situé sur la corde du profil et se déplace en fonction de l’incidence (il se situe en général à 1/4 de la corde du bord d’attaque). Ce point d’application \(P\left(x_{P},y_{P}\right)\) (aussi appelé centre de poussée) de la résultante des forces aérodynamiques \(\overrightarrow{F}=\overrightarrow{F_{p}}+\overrightarrow{F_{t}}\) doit vérifier la relation suivante sur le moment de la résultante par rapport à un point \(O\) quelconque:
avec \(\overrightarrow{F}={\displaystyle \int_{S}-p\overrightarrow{n}dS}\), \(\overrightarrow{dF}=-p\overrightarrow{n}dS\), \(M\left(x_{M},y_{M}\right)\) un point du profil et \(\overrightarrow{n}\) le vecteur normal sortant. En appliquant cette relation, on obtient l’équation de la droite qui porte la résultante, ce qui n’est pas suffisant pour définir la position du centre de poussée. Mais en calculant le centre de poussée sur la ligne moyenne on lève cette indétermination.
On demande de sortir les courbes au format pdf pour le compte rendu:
la courbe des polaires de pression sur le profil calculées avec comsol pour différentes valeurs de \(\beta=\alpha-\theta_{0}\)
la portance et la circulation en fonction de \(\beta=\alpha-\theta_{0}\) calculées avec comsol
l’estimation de l’erreur en fonction de \(\beta=\alpha-\theta_{0}\)
Calcul de la position du centre de poussée en fonction de \(\beta\). On discutera de la stabilité du profil en comparant cette position de \(P\) par rapport au centre de gravité du profil.
3.2.6. Compte rendu#
Écrire un compte rendu de 3 pages maximum, pour déterminer la précision de la simulation comsol, donner l’évolution de la portance en fonction de l’angle d’incidence, ainsi que la loi de portance en fonction de la circulation.
3.2.7. Annexe#
3.2.7.1. exemple de fichier DXF pour un triangle ([0,0,0],[1,0,0],[0.5,1,0])#
999
triangle
0
SECTION
2
ENTITIES
0
LINE
8
0
10
0.0
20
0.0
30
0.0
11
1.0
21
0.0
31
0.0
0
LINE
8
0
10
1.0
20
0.0
30
0.0
11
0.5
21
1.0
31
0.0
0
LINE
8
0
10
0.5
20
1.0
30
0.0
11
0.0
21
0.0
31
0.0
0
ENDSEC
0
EOF
