3.1. Introduction au calcul scientifique avec Python#

Marc BUFFAT, dpt mécanique, Université Lyon 1
(**) voir aussi le cours « Scientific Python Lectures » by Robert Johansson

Mise à disposition selon les termes de la Licence Creative Commons
Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 2.0 France.
%matplotlib inline
import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
# option de mise en page
from IPython.core.display import HTML,display
/tmp/ipykernel_3679072/3841631963.py:6: DeprecationWarning: Importing display from IPython.core.display is deprecated since IPython 7.14, please import from IPython display
from IPython.core.display import HTML,display
3.1.1. Objectifs#
3.1.1.1. Apprendre:#
concept fondamentaux en programmation
différentes techniques de base
démarche de programmation scientifique
syntaxe du langage Python
3.1.1.2. À la fin du cours, vous pourrez:#
résoudre des problèmes scientifiques (à l’aide de Python)
appliquer la démarche de programmation scientifique avec d’autres langages (matlab, scilab, ..)
3.1.2. Fonctionnement d’un ordinateur#
ordinateur = matériel (CPU, mémoire, disque,..) + logiciel (OS, programmes,..)
3.1.2.1. composants d’un ordinateur#
OS
Système d’exploitation (OS) = gestion d’un ordinateur + environement
Linux/Unix = vue abstraite et générique indépendante du matériel
programmes + données
programme = processus
données = fichiers (files, devices, streams)
gestion des droits: notion d’utilisateur (user), groupes (group), autres (other)
super-utilisateur: root
Principes
small is beautiful
generality is better than specificity
communication is important (format ouvert pour les données)
3.1.2.2. programmes / processus#
processus = programme executé sur un ordinateur
pid = numéro du processus
programme (utilisateur ou commande système)
E/S: entrée par défaut (input stream=stdin), sortie par défaut (output stream=stdout)
sortie programme = entrée d’un autre programme : pipe ou |
pge 1 | pge 2 | pge 3
controle des processus: kill pid ou ctrl+C, stop (ctrl+Z) , tache de fond (bg) , ps, top
éxecution des commandes à travers une interface
un terminal avec un shell (interpérteur de commande): bash (avec auto-complétion)
un GUI (gnome, KDE, ..)
syntaxe (attention majuscule # minuscule, espace = séparateur d’arguemnts)
cde [-options] arguments
%%bash
ps -au buffat | head
PID TTY TIME CMD
1885002 tty3 00:00:00 bash
3655868 ? 00:00:00 systemd
3655869 ? 00:00:00 (sd-pam)
3655877 ? 00:00:00 pipewire
3655878 ? 00:00:00 pipewire-media-
3655879 ? 00:06:41 pulseaudio
3655882 ? 00:00:00 gnome-keyring-d
3655886 ? 00:00:05 dbus-daemon
3655892 tty2 00:00:00 gdm-x-session
3.1.2.3. Système de fichiers (Unix)#
vu arborescente abstraite indépendante du matériel à partir de la racine (root) /
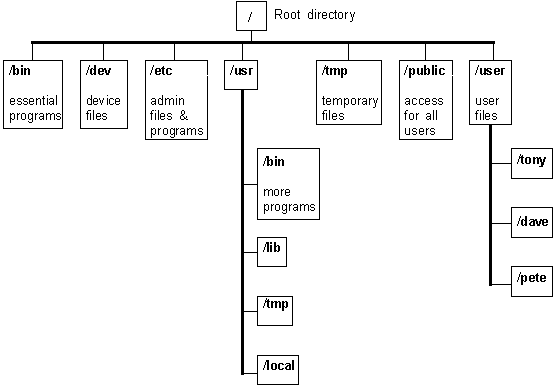
notation
fichier = nom de fichier + répertoire + droits d’accés
/ séparateur de répertoire (directory)
. répértoire courant
.. répértoire parent
pwd : affiche répertoire courant
lien symbolique
fichiers cachés: commence par .
principales commandes
ls : liste des fichiers
mkdir : création répertoire
rm : éfface un fichier
cd : change de répertoire (directory)
help cde : aide
cat file : affiche le contenu du fichier
%%bash
ls -al | head
total 1312
drwxrwxr-x 5 buffat buffat 4096 févr. 24 18:08 .
drwxrwxr-x 4 buffat buffat 4096 févr. 10 10:34 ..
lrwxrwxrwx 1 buffat buffat 39 févr. 10 10:34 Algorithme.ipynb -> MGC1061M/04_Algorithme/Algorithme.ipynb
-rw-rw-r-- 1 buffat buffat 1854 févr. 10 10:34 alunissage.py
-rw-rw-r-- 1 buffat buffat 2136 févr. 10 10:34 anim_pendule.py
-rw-rw-r-- 1 buffat buffat 25430 févr. 10 10:34 BaseProgrammation.ipynb
lrwxrwxrwx 1 buffat buffat 39 févr. 10 10:34 BasePython.ipynb -> MGC1061M/02_BasePython/BasePython.ipynb
-rw-rw-r-- 1 buffat buffat 34861 févr. 10 10:34 BasePython.md
-rw-rw-r-- 1 buffat buffat 27355 févr. 10 10:34 BibliothequeScientifique.ipynb
3.1.3. Execution d’un programme#
3.1.3.1. Calcul de la somme d’une série:#
démarche:
algorithme
programmation
execution du code machine sur l’ordinateur
3.1.3.2. Algorithme de base#
Algorithme Serie(x,n)
somme = 0
pour i de 1 a n
somme=somme + (-1)^(i+1)*x^i/i
retour somme
Ecrire un algorithme plus efficace en notant que:
3.1.3.3. Execution sur un ordinateur#
L’ordinateur (le CPU) n’éxécute que des instructions machines codées en binaire.
Problème: comment transformer un algorithme en langage machine ?
3.1.3.4. Langage machine (binaire)#
suite d’instruction binaire executer par le processeur: 01010111 (suite 0 ou 1 : bits)
représentation en hexadécimal (octet ou bytes):
f8 = 248
instructions et données sont stockées en mémoire (à une adresse donnée)
@000141 instruction f8
spécifiques au processeur (intel, ARM, power, AMD, ..)
spécifique au système d’exploitation OS
%%bash
od -x -N 100 data/a.out
./data/a.out
0000000 457f 464c 0102 0001 0000 0000 0000 0000
0000020 0002 003e 0001 0000 0870 0040 0000 0000
0000040 0040 0000 0000 0000 21b0 0000 0000 0000
0000060 0000 0000 0040 0038 0009 0040 001e 001b
0000100 0006 0000 0005 0000 0040 0000 0000 0000
0000120 0040 0040 0000 0000 0040 0040 0000 0000
0000140 01f8 0000
0000144
Calcul de la serie pour n=20 et x=0.2
Somme de la serie = 0.182322
Log(1+x)=0.182322
3.1.4. Langages de programmation#
conversion d’une programme en code machine
plusieurs centaine de langages différents

-langage le plus complexe: malbolge
3.1.4.1. Langage assembleur#
L’assembleur traduit le code source en code binaire
notation des instructions machines (move, push, load, add, mul)
programme + assembleur = code machine
%%bash
head -15 data/serie.s
.file "serie.C"
.local _ZStL8__ioinit
.comm _ZStL8__ioinit,1,1
.text
.globl _Z5seriedi
.type _Z5seriedi, @function
_Z5seriedi:
.LFB971:
.cfi_startproc
pushq %rbp
.cfi_def_cfa_offset 16
.cfi_offset 6, -16
movq %rsp, %rbp
.cfi_def_cfa_register 6
movsd %xmm0, -40(%rbp)
3.1.4.2. Langage compilé: compilateur#
le compilateur transforme le code source en assembleur (compilation), éffectue l’édition avec des librairies pour obtenir un binaire qui dépend de l’ordinateur cible, mais qui s’exécute sans le compilateur et sans le code source.
C++ Fortran C
programme source + compilateur = programme binaire
programme source = portable
programme binaire = spécifique à l’ordinateur (non portable)
 langage C
langage C
%%bash
head -17 data/serie.C
#include <stdlib.h>
#include <math.h>
#include <iostream>
//
// calcul de la somme de n termes de la serie x-x^2/2+x^3/3-
//
double serie(double x,int n)
{
double coef=x;
double somme=0.0;
for (int i=1; i<=n; i++)
{
somme = somme + coef/i;
coef = -coef*x;
}
return somme;
}
%%bash
g++ data/serie.C -o serie
./serie
Calcul pour n=20 et x=0.2
Somme = 0.182322
Log(1+x)= 0.182322
3.1.4.3. Langage interprété:#
l’interpéteur exécute de façon interactive chaque ligne du fichier pour la traduire en code machine et l’execute interactivement. Pour exécuter le code, on a donc toujours besoin de l’interpréteur et du code source.
Python, Matlab
programme + interpréteur
portable = indépendant du système (Linux, MacOS, Windows)
3.1.4.3.1. Matlab (Matrix Laboratory)#
Matlab est un logiciel propriétaire qui est une boite à outils (toolbox) de calcul matriciel et numérique développé par Mathworks Inc. Il fonctionne sous Windows, Mac et Unix et permet d’écrire rapidement des scripts pour faire du calcul scientifique.
De nombreuses alternatives libres et de qualité existent, et notamment les logiciels : Scilab, Octave et surtout Python avec numpy.
%%bash
cat data/serie.m
% programme matlab
% ================
x=0.2; n=20;
% calcul de la serie
coef=x;
somme=0.0;
for i=1:n;
somme = somme+coef/i;
coef = -coef*x;
end;
display(sprintf('Calcul de la serie pour x=%g et n=%d',x,n))
display(sprintf('somme = %g',somme))
display(sprintf('log(1+x) = %g',log(1+x)))
exit
3.1.4.3.2. langage python#
Python est un language de programmation moderne de haut niveau, logiciel libre, généraliste, multi-plateformes, multi-architecture, multi-OS (linux, windows, MacOS,..). Un programme python peut s’executer sur un tout petit raspberry Pi à 30€ (ARM), sur des smartphones, des portables, des PC jusqu’aux super-calculateurs HPC avec \(10^9\) coeurs de calcul.
%%bash
cat data/serie.py
#! /usr/bin/env python
from math import log
def serie(x,n):
""" calcul de la somme de n termes de la serie x-x^2/2+x^3/3- """
coef=x
somme=0.0
for i in range(1,n+1):
somme = somme + coef/i
coef = -coef*x
return somme
#
x=0.2
n=20
print("Calcul de la serie pour x=",x," et n=",n)
print("somme = ",serie(x,n))
print("log(1+x) = ", log(1+x))
%%bash
python data/serie.py
Calcul de la serie pour x= 0.2 et n= 20
somme = 0.18232155679395456
log(1+x) = 0.1823215567939546
3.1.5. Historique des langages de programmation#
Années 1950 (approches expérimentales) :
FORTRAN, LISP, COBOL…
Années 1960 (langages universels) :
ALGOL, PL/1, PASCAL…
Années 1970 (génie logiciel) :
C, MODULA-2, ADA…
Années 1980 (programmation objet) :
C++, Eiffel…
Années 1980 (boites à outils):
LabView, Matlab…
Années 1990 (langages interprétés objet) :
Java, Perl, Python…
3.1.5.1. Langages les plus utilisées par les scientifiques#
Pour le calcul intensif (HPC) (Argonne Lab)
C,C++
Fortran
Python
Matlab est très utilisé pour le traitement des données, mais peut être avantageusement remplacer par Python avec ses librairies numpy et matplotlib et pandas
3.1.6. Exigences du calcul scientifique#
« Le logiciel (software) est une des pierres angulaires de la science moderne. Sans logiciel, la science du vingt et unième siècle serait impossible. Mais sans de meilleurs logiciels, la science ne peut pas progresser » [http://sciencecodemanifesto.org/]
Réplicabilité et de reproductibilité sont des pierres angulaires de la méthode scientifique. En ce qui concerne le travail numérique, se conformer à ces concepts a des implications pratiques suivantes:
Réplicable: L’auteur d’un article scientifique qui implique des calculs numériques doit être en mesure de relancer les simulations et de reproduire les résultats sur demande. D’autres scientifiques devraient également être en mesure d’effectuer les mêmes calculs et d’obtenir les mêmes résultats, compte tenu des informations sur les méthodes utilisées dans une publication.
Reproductible: Les résultats obtenus à partir de simulations numériques doivent être reproductibles avec une mise en oeuvre indépendante du procédé, ou en utilisant un procédé tout à fait différent.
En résumé: un résultat scientifique solide doit être reproductible, et une étude scientifique solide doit être réplicable.
importance de la documentation
importance de la validation
importance de la maîtrise du code et des transformations de données (logiciels libres)
Modèle mathématique
Discrétisation numérique: solution approchée
Recherche solution algorithmique
Programmation
Validation
3.1.6.1. Démarche du calcul scientifique#
3.1.7. Documentation#
Python. The official Python web site.
Python tutorials. The official Python tutorials.
Think Python. “”How to Think Like a Computer Scientist”” by Allen B. Downey (free book).
COURS InProS “”Introduction à la Programmation Scientifique””
3.1.7.1. Installation (logiciel libre)#
Distribution pour Linux, Windows, Mac
accès aux serveurs Jupyter à l’UCB Lyon 1:
