Écoulement autour d’un profil NACA

Contenu

3.2. Écoulement autour d’un profil NACA#

Écoulement autour d’un profil

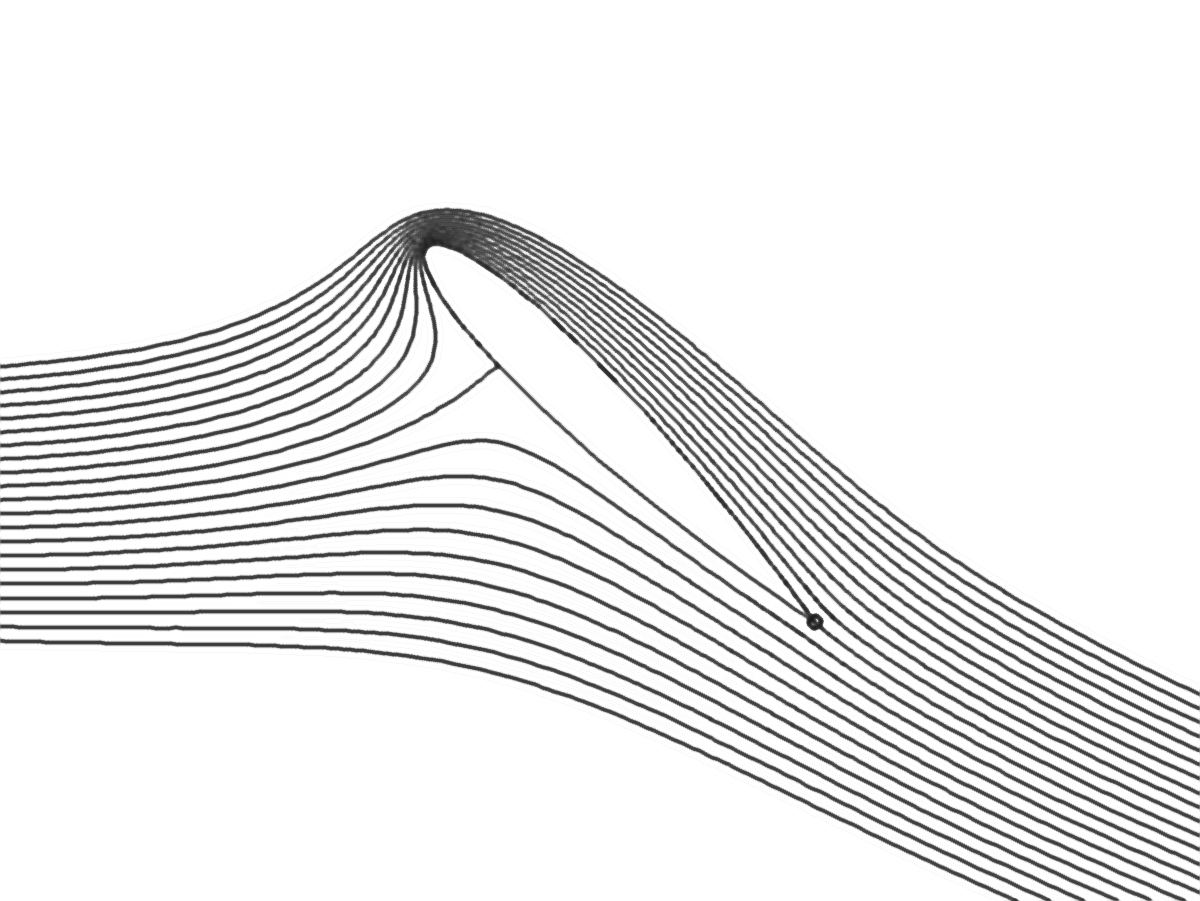
Bilan des forces sur un avion

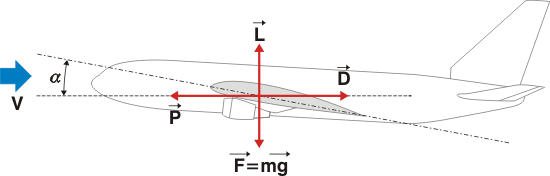
3.2.1. Théorie de l’aile#

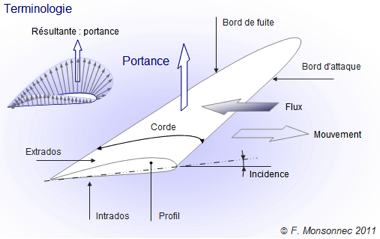
Les différentes (fausses) théories

théorie du temps de transit (Bernoulli)
théorie effet Venturi

Oui mais l’écoulement autour d’une plaque plane génère une portance !!

3.2.1.1. théorie de kutta-joukowsky#

Génération d’une circulation de vitesse $\Gamma=\oint\,\overrightarrow{u}.\overrightarrow{dl}$ autour du profil pour que l’écoulement autour du bord de fuite ne le contourne pas (condition de Kutta)!!!.

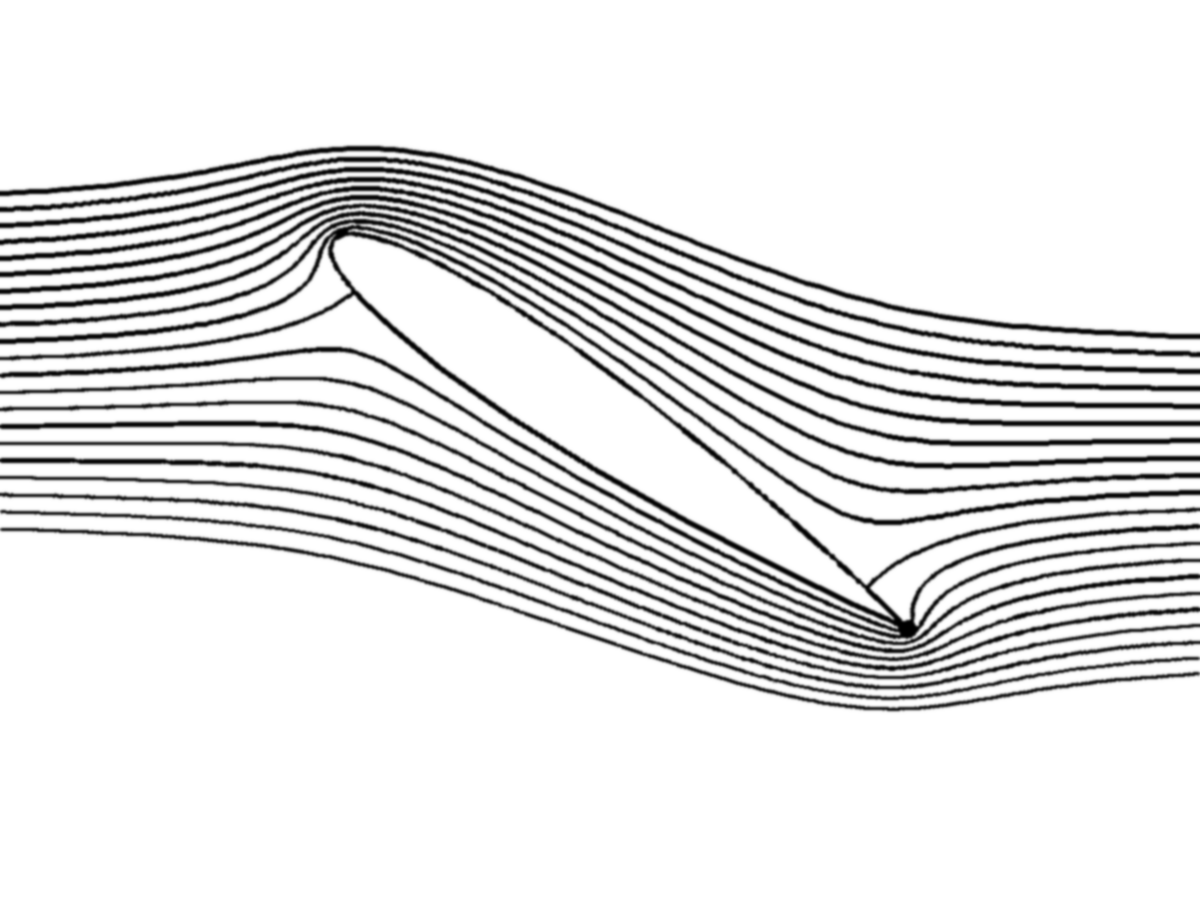
../_images/solpot0.png — Fig. 3.1 solution sans condition de Kutta Joukowsky#

../_images/solpot1.png — Fig. 3.2 solution avec condition de Kutta Joukowsky#

Cette circulation $\Gamma$ s’écrit pour un profil symétrique ($a$ rayon du cercle générateur):

\[\Gamma=4\pi U_{0}a\sin\alpha\approx4\pi U_{0}a\alpha\]

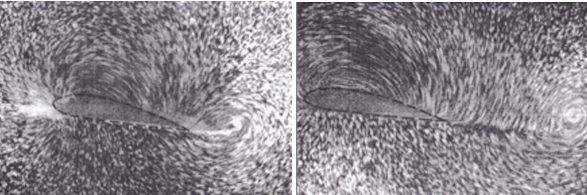
../_images/TheoTourbillonInitiateur.png — Fig. 3.3 génération du tourbillon de bout d’aile#

../_images/TheoTourbillonNouveau.png — Fig. 3.4 tourbillon de bout d’aile#

3.2.1.2. Force de portance#

Théorie de la portance

\[F_{p}=\rho U_{0}\Gamma\]

Analyse dimensionnelle

\[\frac{F_{p}}{\frac{1}{2}\rho U_{0}^{2}L}=f(R_{e},\alpha)\]

3.2.2. Définition du profil#

On veut étudier l’écoulement autour d’un profil NACA pour calculer la portance du profil en fonction de l’angle d’incidence $\alpha$.

3.2.2.1. Définition d’un profil NACA#

Un profil NACA est un profil d’aile standardisé définie à partir de 3 paramètres:

l’épaisseur relative $t$
la cambrure maximale $m=y_{a}$ au point $p=x_{a}$ de la ligne moyenne

3.2.2.1.1. profil symétrique#

Dans ce cas $y_{a}=x_{a}=0$ et le seul paramètre est l’épaisseur relative $t$.

L’extrados est donné par la courbe $y_{e}=F(x)$ suivante et l’intrados par la courbe symétrique $y_{i}=-F(x)$ pour $0\leq x\leq L_{c}$

\[F(x)=5.0\,t\left(0.2969\,\sqrt{x}-0.1260\,x-0.3516\,x^{2}+0.2843\,x^{3}-0.1036\,x^{4}\right)\,\]

La longueur de la corde $L_{c}$ suivant $x$ est donnée par la racine de $F(L_{c})=0$, i.e. $L_{c}=1$ (calcul sans dimension);

Un profil NACA symétrique à 4 chiffres est donné par la nomenclature NACA00yz où les 2 chiffres $yz$ représente l’épaisseur relative du profil $t=yz/100$. Les profils NACA suivants sont des profils symétriques: NACA0009 et NACA0012.

3.2.2.1.2. profil cambré#

Dans ce cas on donne la ligne moyenne du profil en fonction de $x_{a}$ et $y_{a}$. Cette ligne moyenne a pour équation en fonction de $x$

\[\begin{split}y_{m}=\left\{ \begin{array}{l} y_{a}\frac{(2x_{a}-x)\,x}{x_{a}^{2}}\,\mbox{ si }0\leq x\leq x_{a}\\ y_{a}\frac{(1-x)(1+x-2x_{a})}{(1-x_{a})^{2}}\mbox{ si }x\leq x\leq L_{c} \end{array}\right.\end{split}\]

L’équation de l’extrados $\{y_{e},x_{e}\}$ est obtenu à partir de cette ligne moyenne, en introduisant l’angle $\theta$

\[\theta(x)=\frac{dy_{m}}{dx}\]

et la fonction $F(x)$précédente:

\[\begin{split}\begin{align} x_{e}(x) & = x-F(x)\,\sin(\theta(x))\\ y_{e}(x) & = y_{m}+F(x)\,\cos(\theta(x))\,\,\,\,\mbox{ pour }0\leq x\leq L_{c}\end{align}\end{split}\]

L’équation de l’intrados $\{x_{i},y_{i}\}$ correspond à l’équation symétrique en $y$

\[\begin{split}\begin{align} x_{i}(x) & = x+F(x)\,\sin(\theta(x))\\ y_{i}(x) & = y_{m}-F(x)\,\cos(\theta(x))\,\,\,\,\mbox{ pour }0\leq x\leq L_{c}\end{align}\end{split}\]

La longueur de la corde $L_{c}$ vérifie $y_{e}(L_{c})=y_{i}(L_{c})$

Un profil NACA cambré à 4 chiffres est donnée par la nomenclature NACAwxyz où les 2 chiffres $yz$ représentent l’épaisseur relative du profil ($t=yz/100$), le chiffre $w$ la courbure relative en % ($y_{a}=w/100$) et le chiffre $x$ la position de la flèche de la ligne moyenne en $1/10$ de corde ($x_{a}=x/10$). Les profils NACA suivants sont des profils cambrés : NACA6512, NACA6412, NACA2412, NACA4412, NACA4415.

Un profil NACA cambré à 5 chiffres est donnée par la nomenclature NACAwxxyz où les 2 chiffres $yz$ représentent l’épaisseur relative du profil ($t=yz/100$), le chiffre $w$ la courbure relative en % ($y_{a}=w/100$) et les 2 chiffres chiffres $xx$ la position de la flèche de la ligne moyenne en $2/100$ de corde $(x_{a}=2xx/100$). Les profils NACA suivants sont des profils cambrés à 5 chiffres: NACA23112 et NACA16020.

3.2.2.2. Modélisation de l’écoulement autour d’un profil NACA symétrique#

L’écoulement autour d’un profil symétrique en incidence est représenté sur la figure ci-dessous:

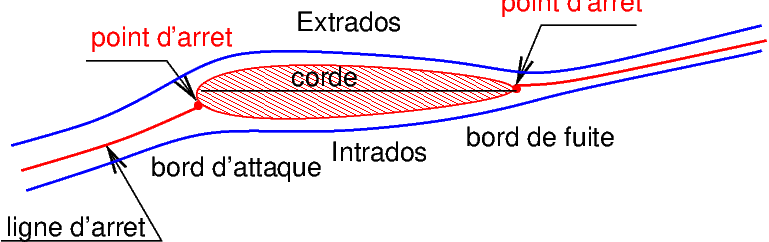
../_images/schema.png — Fig. 3.5 écoulement autour d’un profil symétrique#

L’écoulement avec incidence positive présente un point d’arrêt sous le bord d’attaque, et un point d’arrêt sur le bord de fuite. La répartition de pression est donnée sur la figure ci-dessous ou on a tracé le coefficient de pression $C_{p}$ :

\[C_{p}=\frac{p-p_{0}}{\frac{1}{2}\rho U_{0}^{2}}\]

en fonction de la corde. On voit qu’à l’extrados il est négatif (zone de dépression) et positif à l’intrados (zone de surpression) sauf tout près du bord d’attaque où il y a une forte dépression. En l’absence de frottement visqueux, la force de pression qui s’exerce sur le profil est une force de portance.

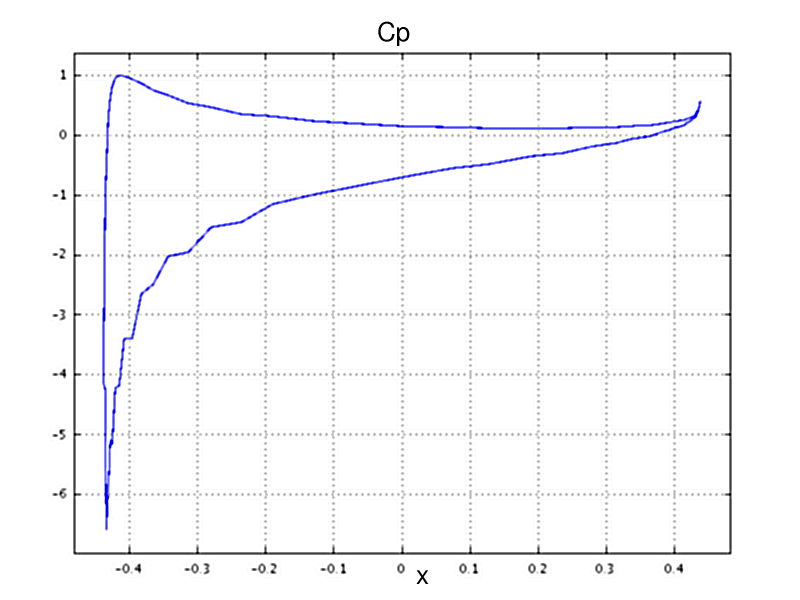
../_images/cp.png — Fig. 3.6 coefficient de portance $C_p$#

Pour modéliser cet écoulement, on utilise un modèle potentiel. Le champ de vitesse $\overrightarrow{U}$ découle d’un potentiel $\Phi$ , et aussi d’une fonction de courant $\Psi$. Les conditions aux limites sont:

à l’infini (frontière $\Gamma_{0}$), la vitesse est égale à $U_{0}$ avec un angle d’incidence $\alpha$: $\overrightarrow{U}=U_{0}[\cos\alpha,\sin\alpha]$
sur le profil (frontière $\Gamma_{1}$), la vitesse est tangente au profil (glissement): $\overrightarrow{U}.\overrightarrow{n}=0$

Mais sur le profil, on doit imposer une condition supplémentaire, qui est la circulation de vitesse $\kappa$ autour du profil $\Gamma_{1}$:

\[\kappa=\oint_{\Gamma_{1}}\overrightarrow{U}.\overrightarrow{dl}\]

C’est cette circulation qui crée la portance. La valeur de cette circulation $\kappa$ doit être telle que l’écoulement au bord de fuite soit régulier (i.e. que le point d’arrêt soit sur le bord de fuite). C’est la condition de Kutta Joukovski. Sur les figures ci-dessous, on a représenté à gauche une solution potentielle avec $\kappa=0$ (non physique) et à droite la solution avec la valeur de $\kappa$ satisfaisant la condition de Kutta Joukovski.

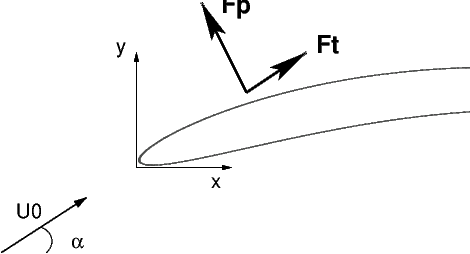
3.2.2.3. Calcul du point d’application#

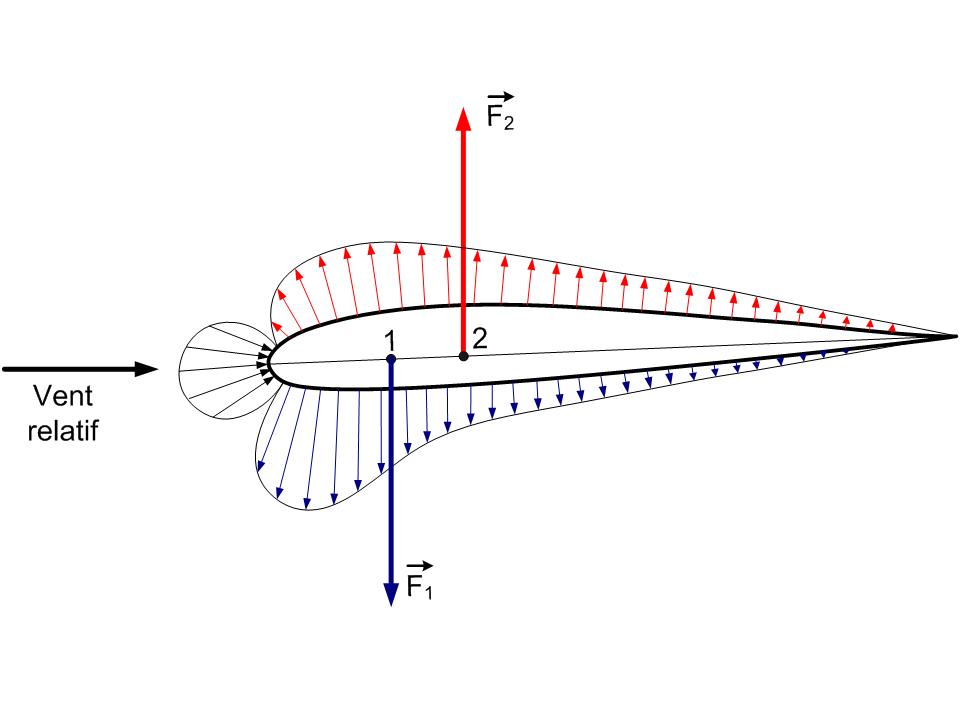
../_images/portance.jpg — Fig. 3.9 Portance sur un profil#

Le point d’application $P\left(x_{P},y_{P}\right)$ (aussi appelé centre de poussée) de la résultante des forces aérodynamiques $\overrightarrow{F}=\overrightarrow{F_{p}}+\overrightarrow{F_{t}}$ doit vérifier la relation suivante sur le moment de la résultante par rapport à un point $O$ quelconque:

\[\overrightarrow{OP}\wedge\overrightarrow{F}=\int_{S}\overrightarrow{OM}\wedge\overrightarrow{dF}\]

avec $$\overrightarrow{F}={\displaystyle \int_{S}-p\overrightarrow{n}dS} \mbox{ et } \overrightarrow{dF}=-p\overrightarrow{n}dS$$

$M\left(x_{M},y_{M}\right)$ est un point du profil et $\overrightarrow{n}$ le vecteur normal sortant. En appliquant cette relation, on obtient l’équation de la droite qui porte la résultante, ce qui n’est pas suffisant pour définir la position du centre de poussée. On calcul donc sa position sur la ligne moyenne.