Cours algorithmique

3. Cours algorithmique#

Marc Buffat dpt mécanique, UCB Lyon 1

algorithme 
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from IPython.display import HTML

3.1. Algorithmes numériques de base#

Un algorithme est une suite finie et non ambigüe d’opérations ou d’instructions permettant de résoudre un problème. Les algorithmes sont connus depuis l’antiquité (Euclide).

Le mot algorithme vient du nom du mathématicien perse du 9ième siècle

  • Abu Abdullah Muhammad ibn Musa al-Khwarizmi.

L’algorithmique correspond à la phase préparatoire avant une quelconque programmation. Elle permet de décrire un problème sous une forme que l’on peut ensuite programmer sur un ordinateur et ceci dans un langage naturel, indépendant d’un langage de programmation.

algorithme numérique suite finie et non ambiguë d’opérations ou d’instructions sur des nombres permettant de résoudre un problème.

Et il n’est pas nécessaire d’avoir un ordinateur pour exécuter un algorithme!

3.2. Méthode d’analyse algorithmique#

  1. programmation procédurale en informatique, la programmation procédurale est un paradigme qui se fonde sur le concept d’appel procédural.

Une procédure, aussi appelée routine, sous-routine ou fonction contient simplement une série d’étapes à réaliser en fonction de données (arguments) et fournit des résultats (valeur).

  1. top down algorithm / design

on découpe le problème en sous problèmes plus simples

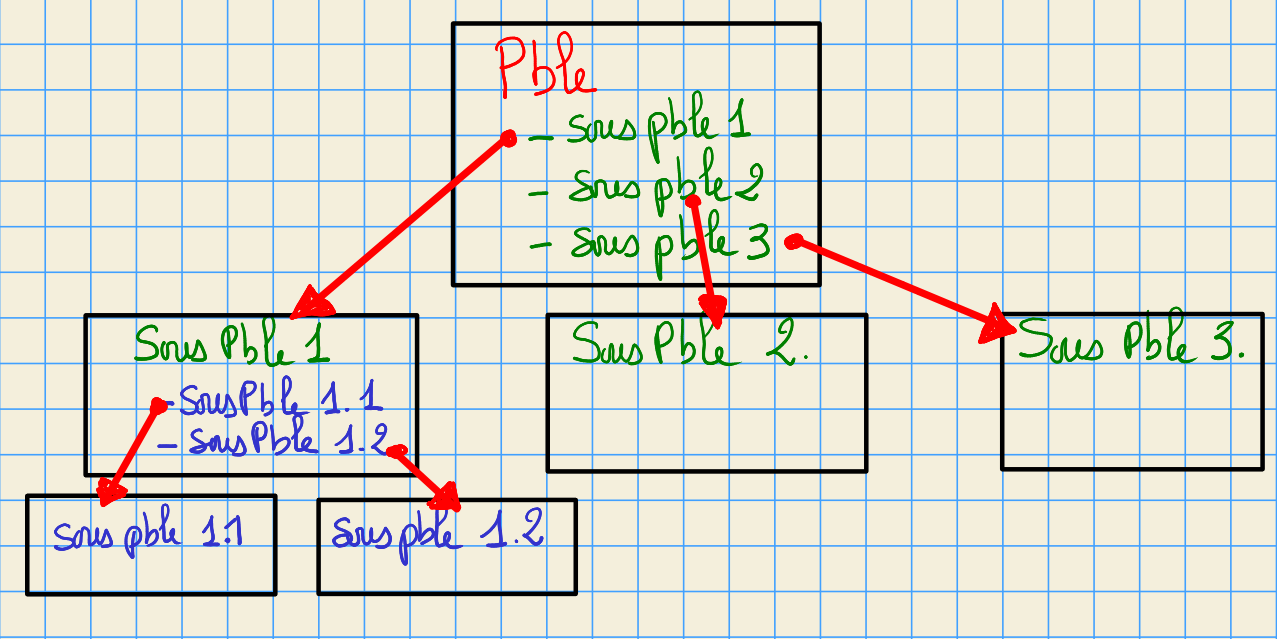
../_images/analyse_topdown.png

  1. bottom up programming

on programme d’abord les algorithmes des sous-problèmes, avant de passer à la résolution globale:

 - utilisation de librairies
 - définition des fonctions
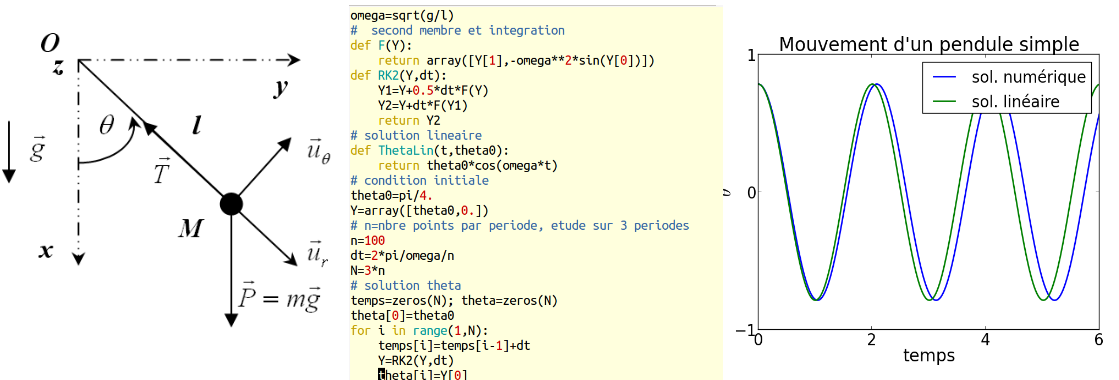
../_images/algorithme.png

3.3. Différents types d’algorithme#

  1. algorithme itératif

Un algorithme itératif est basé sur les procédures d’itération que sont le Tant que et le Pour. Il réalise donc une boucle jusqu’à ce que la condition d’arrêt soit respectée (test , nbre d’itérations, ..).

  1. algorithme récursif

récursion méthode algorithmique où la solution du problème s’exprime en fonction de solutions du même problème, mais sur des données plus petites.

3.3.1. Exemple : calcul de n!#

  1. version itérative

    \[ n! = \prod_{i=1}^n i \]

  2. version récursive

    \[ n! = n * (n-1)! \]

programmation dans le notebook !

3.4. Algorithme d’Euclide#

Soit une pièce rectangulaire de taille \(a \times b\), déterminer la taille du plus grand carré permettant un pavage exacte de la pièce:

Analyse

  • propriétés

    1. pavage(a,b) = pavage(a-b,b) si a>b

    2. pavage(a,b) = pavage(a,b-a) si a<b

    3. pavage(a,b) = a si a=b

  • algorithmes

    1. version récurrente

    2. version itérative

def PGCD(a,b):
    if a==b :
        return a
    elif a>b :
        return PGCD(a-b,b)
    else :
        return PGCD(a,b-a)

%timeit PGCD(100,75)

377 ns ± 5.66 ns per loop (mean ± std. dev. of 7 runs, 1,000,000 loops each)

def PGCD1(a,b):
    while a!=b :
        if a>b :
            a = a-b
        else:
            b = b-a
    return a

timeit PGCD1(100,75)

242 ns ± 1.17 ns per loop (mean ± std. dev. of 7 runs, 1,000,000 loops each)

3.5. Algorithme du calcul du déterminant d’une matrice#

soit \(A\) une matrice d’ordre \(n\), la méthode de Cramer permet le calcul récursif du déterminant par développement par rapport à la 1ere colonne

\[ det(A) = \sum_{k=1}^n (-1)^{k+1} A_{k,1} \times det(A^k) \]

où \(A^k\) est la sous-matrice obtenu par élimination de la colonne 1 et de la ligne \(k\) de \(A\)

Pour une matrice de dimension 1 $\( det(a) = a \)$

### Version recursive
def determinant(A):
    
    return

3.5.1. Algorithme déterminant#

 Algorithme determinant(A)
     n = dim(A)
     si n==1 alors
         retour A[0,0]
     fin si
     # A1 sous matrice d'ordre n-1
     A1 = tableau(n-1,n-1)
     det = 0
     signe = 1
     # développement par rapport a la 1ere colonne
     pour k de 0 a n-1
         # sous matrice Ak
         A1[0:k,:] = A[0:k ,1:n]
         A1[k:,:]  = A[k+1:,1:n]
         det = det + signe*A[k,0]*determinant(A1)
         signe = -signe
         fin pour
     retour det

3.5.2. Programme Python (solution)#

from numpy.linalg import det

def determinant(A):
    """ calcul du déterminant d'une matrice A """
    n=A.shape[0]
    if n==1 :
        return A[0,0]
    A1 = np.zeros((n-1,n-1))
    det = 0.
    signe = 1
    for k in range(n):
        A1[0:k,:] = A[0:k  ,1:n]
        A1[k: ,:] = A[k+1:n,1:n]
        det = det + signe*A[k,0]*determinant(A1)
        signe = -signe
    return det
# verification
M = np.array([[2.,0.,0],[0.,3.,0],[0,0,4.]])
delta = determinant(M)
print("determinant :",delta, det(M))

determinant : 24.0 23.999999999999993

# comparaison avec scipy
M = np.random.rand(8,8)
print(M)
delta = determinant(M)
print("determinant M:",delta,det(M))

[[0.73282351 0.680793   0.83755284 0.83175353 0.57270765 0.58147185
  0.70494612 0.96239902]
 [0.02207577 0.92802574 0.13752665 0.6131575  0.0411426  0.35056193
  0.13331779 0.99280043]
 [0.74109    0.72625978 0.85785765 0.93249469 0.50421179 0.92131726
  0.24303556 0.30953265]
 [0.63911709 0.5057217  0.4654358  0.54257145 0.08170261 0.35807291
  0.01585477 0.40325331]
 [0.21039234 0.79895253 0.41034214 0.44127221 0.21432768 0.48922324
  0.07342315 0.32519869]
 [0.22902869 0.90919905 0.1757214  0.99892266 0.3036899  0.63421537
  0.10613361 0.40272792]
 [0.35207341 0.65868703 0.66009863 0.61058958 0.93373945 0.25940652
  0.59188581 0.22823346]
 [0.36839112 0.17049951 0.2850186  0.40398784 0.99516284 0.90958383
  0.0414199  0.88986572]]
determinant M: 0.011612777028329599 0.011612777028329597

## Efficacité
%time determinant(M)

CPU times: user 144 ms, sys: 1 μs, total: 144 ms
Wall time: 144 ms

0.011612777028329599

%time det(M)

CPU times: user 42 μs, sys: 1 μs, total: 43 μs
Wall time: 45.1 μs

0.011612777028329597

3.6. Algorithmes classiques#

  • méthode de Newton

  • méthode des trapèzes

  • méthode d’Euler

  • tour de Hanoi

  • tri par insertion

  • bubble sort

3.7. Bibliothèques scientifiques#

  • numpy

  • scipy

3.8. FIN#

Contenu