Tableaux avec numpy et courbes avec matplotlib

3.3. Tableaux avec numpy et courbes avec matplotlib#

Marc BUFFAT, dpt mécanique, Université Lyon 1 et [1]

images/numpy_array.png

from IPython.display import display, Markdown, clear_output
def printmd(string):
    display(Markdown(string))
from metakernel import register_ipython_magics
register_ipython_magics()

3.3.1. Introduction#

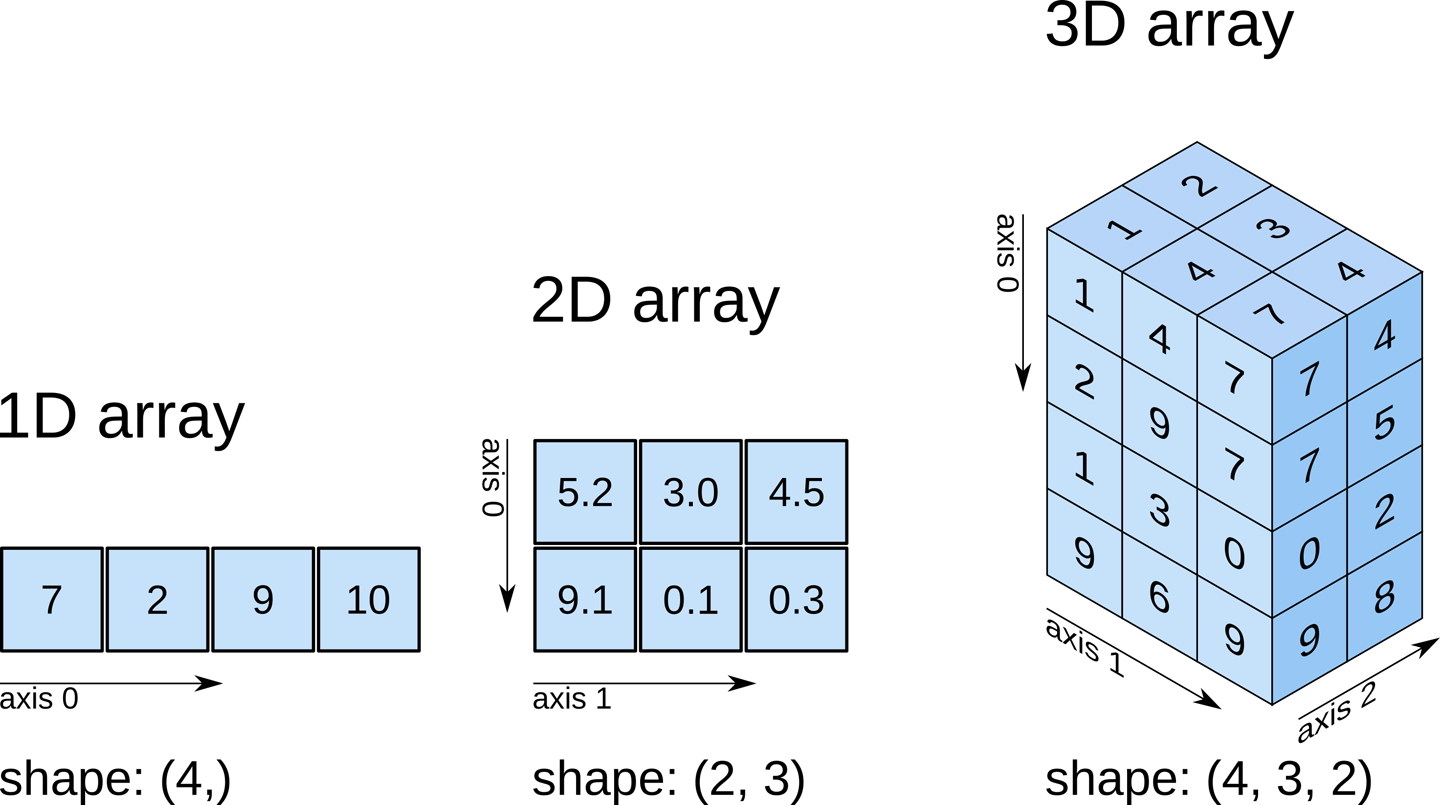
Pour beaucoup d’applications en mécanique, on est amené à manipuler des tableaux qui sont des séquences de données du même type. Ils ressemblent beaucoup aux listes, à l’exception de la contrainte sur le type des éléments. Cela apporte un énorme avantage en termes d’efficacité aux tableaux par rapport aux listes. Ainsi, les méthodes sur les tableaux s’exécutent beaucoup plus rapidement que celles sur les listes.

Grâce aux bibliothèques, le langage Python permet de traiter efficacement des applications numériques en sciences et technologie. Pour le calcul scientifique, la bibliothèque la plus importante est NumPy (Numerical Python), qui fournit les structures de données de tableaux (array) à n dimensions ( ndarray), avec toutes les fonctions, opérations et algorithmes pour les calculs d’algèbre linéaire. Nous utiliserons aussi la bibliothèque Matplotlib pour tracer les données en deux dimensions.

3.3.2. Importation de bibliothèques#

En Python, les bibliothèques ne sont pas chargées automatiquement, mais doivent etre importés explicitement en utilisant la commande import. Par exemple, pour importer NumPy, avec toutes ses fonctions d’algèbre linéaire, on utilise

# soit
import numpy
# ou
import numpy as np

La deuxième forme, que nous utiliserons, permet de donner un nom abrégé (ici sp) à la bibliothèque, que l’on utilise à la place du nom de la bibliothèque (i.e. numpy).

Une fois la bibliothéque chargée, on peut utiliser les fonctions de la bibliothèque en ajoutant devant le nom de la bibliothéque ou son nom abrégé. Par exemple, certaines fonctions couramment utilisées avec numpy sont:

Suivez les liens pour voir la documentation de ces fonctions NumPy très utiles, ou utiliser le menu Aide->Numpy Reference!

import numpy as np

3.3.3. Création de tableaux#

Pour créer un tableau NumPy à partir d’une liste existante de valeurs ( homogènes), on utilise numpy.array():

   numpy.array([3, 5, 8, 17])

NumPy propose de nombreuses façons de créer des tableaux (cliquez sur le lien).

Par exemple numpy.ones() et numpy.zeros() créent des tableaux remplis de uns et de zéros, respectivement. On passe en argument le nombre souhaité d’éléments du tableau.

Créer dans la cellule suivante un tableau de 1 de dimension 5 et un tableau de 0 de dimension 3.

# écrire votre code ici

# solution

Une autre fonction numpy.arange() crée un tableau de valeurs régulièrement espacées de pasdans un intervalle définit [debut,fin] mais où finest exclu.

Syntaxe:

numpy.arange(debut, fin, pas)

où debut vaut par défaut zéro,fin est exclus du tableau et pas a une valeur par défaut de 1.

Utiliser les commandes suivantes et analyser le résultat:

np.arange(4)
np.arange(2, 6)
np.arange(2, 6, 2)
np.arange(2, 6, 0.5)

# écrire votre code ici

la fonction numpy.linspace() est similaire à numpy.arange(), mais utilise un nombre d’échantillons N au lieu du pas. Il renvoie un tableau de N valeurs avec des nombres régulièrement espacés sur l’intervalle spécifié [debut,fin] où finest inclu.

Syntaxe:

numpy.linspace(debut,fin,N)

Utiliser les commandes suivantes et analyser les résultats:

  np.linspace(2.0, 3.0)
  len(np.linspace(2.0, 3.0))
  np.linspace(2.0, 3.0, 6)
  np.linspace(-1, 1, 9)

# écrire votre code ici

3.3.4. Opérations sur les tableaux#

En affectant un tableau à une variable, on peut ensuite faire simplement des opérations sur le tableau, qui correspondent à des opérations éffectuées sur chaque élément du tableau (i.e. terme à terme).

Utiliser les commandes suivantes et analyser les résultats

   X = np.linspace(-1, 1, 9)
   Y = X * X
   Z = np.sqrt(Y)
   W = X + Z

# écrire votre code ici

Nous pouvons également diviser des tableaux, mais il faut faire attention à ne pas diviser par zéro. Cette opération se traduira par un nan qui signifie Not a Number. Python effectuera toujours la division, mais nous informera du problème.

Tester le résultat de l’opération

   X / Y

# écrire votre code ici

3.3.5. Tableaux multidimensionnels#

3.3.5.1. tableaux 2D#

NumPy peut créer des tableaux de N dimensions. Par exemple, un tableau 2D ressemble à une matrice et est créé à partir d’une liste imbriquée comme suit:

  A = np.array([[1, 2], [3, 4]])

Les opérations sur matrices sont des opérations terme à terme sur chaque élément.

A partir des 2 matrices A, B suivantes, affichez le résultat de

  1. A + B

  2. A - 2B

  3. A * B

questions

  • Que se passet-t-il si les matrices ne sont pas de la même dimension ?

  • Peut on utiliser une notation implicite pour les opérations p.e. 2B ?

A = np.array([[1, 2], [3, 4]])
B = np.array([[1, -1], [0, 1]])
# votre code ici

Attention la dernière opération A*B ne correspond pas à la multiplication matricielle (réfléchissez pourquoi ?)

La multiplication matricielle est obtenue avec l’opérateur @ ou la fonction numpy.dot()

    A @ B
    np.dot(A,B)

Dans la cellule suivante calculer le produit matriciel des 2 matrice A et B.

Si X est le vecteur donné ci dessous, calculer le produit matrice vecteur \(A X\)

Que fournit l’expression

    A*X

X = np.array([1,2])

# votre code ici

3.3.5.2. algèbre linéaire#

En mécanique, on doit manipuler assez souvent des systèmes d’équations linéaires. Numpy possède une sous-bibliothèque d’algèbre linéaire linalg fournissant les fonctions suivantes pour un système linéaire $\( A X = D \)$

  • np.linalg.det(A) calcule le déterminant de A

  • np.linalg.inv(A) calcule \(A^{-1}\) l’inverse de A

  • np.linalg.solve(A,D) calcule la solution X du système linéaire \(A X = D\)

  • np.linalg.eigvals(A)calcul les valeurs propres de A

  • np.linalg.eig(A)calcul les valeurs et les vecteurs propres de A

remarque importante

  1. pour résoudre un système linéaire numériquement on n’utilise jamais la méthode mathématique \( X = A^{-1} D\) en calculant \(A^{-1}\) l’inverse de A, car même si on sait calculer l’inverse de A numériquement avec np.linalg.inv(A). Cette méthode est sujette à des erreurs importantes d’arrondie et est inefficace. On utilise à la place la méthode d’élimination de Gauss (que vous verrez dans le cours de méthodes numériques) qui correspond à la fonction np.linalg.solve(A,D).

  2. pensez à consultez la documentation numpy et numpy.linalg (menu Aide->numpy)

exercise En utilisant le vecteur D suivant et la matrice A précédente, calculer la solution Y de $\( A Y = D \)$ et mettre le résultat dans la variable Y

Comment peut-on vérifier le résultat ?

D = np.array([5,11])
# votre code ici
Y = 0

3.3.5.3. sélection des éléments d’un tableau#

Pour accéder aux éléments d’une matrice on utilise la notation classique [ligne,colonne].

Pour sélectionner une ligne entière on utilise : à la place de ligne, et idem pour une colonne.

Pour sélectionner une partie du tableau on utilise la notation debut:fin pour afficher les valeurs de debut à fin (attention fin est exclu)

Exercices

  1. afficher la valeur de la première ligne, première colonne de A,

  2. afficher la valeur de la première ligne, deuxième colonne de A,

  3. afficher la première ligne de A,

  4. afficher la seconde colonne de A.

# votre code ici

3.3.5.4. boucle sur les éléments d’un tableau#

la bibliothèque numpy possède de nombreuses fonctions pour manipuler des tableaux. par contre dans certain cas on doit effectuer des calculs particuliers qui nécessitent de faire des boucles itératives sur les éléments d’un tableau.

Python offre divers formes de boucles itératives à utiliser suivant les besoins. Nous verrons ici uniquement des boucles sur des tableaux 1D ou vecteurs:

3.3.5.4.1. boucle sur les valeurs#

soit un tableau Tab, on s’intéresse à la valeur val des éléments successifs du tableau? C’est la boucle classique en Python:

   for val in Tab:
      print(val)

exercise on veut déterminer le nombre de valeurs d’un tableau qui sont supérieures à une valeur donnée. Par exemple dans le tableau X suivant, on veut connaître le nombre de valeurs supérieure à 0.5

X = np.random.rand(5)
print(X)
# votre code ici

[0.8382678  0.67753927 0.18222755 0.76499179 0.80958286]

3.3.5.4.2. boucle sur les indices et les valeurs#

Si l’on souhaite modifier les valeurs du tableau, la boucle précédente ne le permet. Il faut avoir accés aussi à l’indice i de la valeur val dans le tableau Tab.

En python la boucle s’écrit alors:

   for i,val in enumerate(Tab):
      print(val,"se trouve a l'indice ",i)

exercise en reprenant l’exemple précédent, on souhaite écrêter le tableau X en remplaçant les valeurs supérieures à 0.5 par 0.5.

# votre code ici

3.3.5.4.3. boucle sur les indices uniquement#

enfin on peut vouloir faire une boucle uniquement sur les indices, dans le cas ou manipule plusieurs tableaux.

En python la boucle s’écrit alors:

   for i in range(len(Tab)):
      print("pour l'indice ",i," la valeur vaut ",Tab[i])

On a besoin de la taille du tableau Tab que l’on peut obtenir par la fonction générique len() ou la méthode .size() pour un tableau ndarray

exercise en reprenant l’exemple précédent, on souhaite écrêter le tableau X en remplaçant les valeurs supérieures à 0.5 par la valeur d’un autre tableau Y de même dimension que X

Y = 0.5*np.random.rand(5)
# votre code ici

3.3.5.5. Aliasing#

lors d’un instruction d’affectation

    X = Y

  • si X,Y sont des scalaires pas d’aliasing

  • si X,Y sont des listes ou des tableaux , alors aliasing

  • utilisation d’une copie explicite

print("pas d'aliasing avec les scalaires")
x=2
y=x
x=3
print(x,"#",y)

pas d'aliasing avec les scalaires
3 # 2

print("mais aliasing avec les listes et tableaux")
X=[1,2,3]
Y=X
X[0]=0
print(X,"==",Y)

mais aliasing avec les listes et tableaux
[0, 2, 3] == [0, 2, 3]

print("pas d'aliasing si copie explicite des valeurs")
X=np.array([1,2,3])
Y=X.copy()
X[0]=0
print(X,Y)
Y=np.zeros(X.shape)
Y[:]=X
X[0]=3
print(X,Y)

pas d'aliasing si copie explicite des valeurs
[0 2 3] [1 2 3]
[3 2 3] [0. 2. 3.]

3.3.5.5.1. Question test#

%activity /usr/local/commun/ACTIVITY/IntroPython/questionAlgorithme1

3.3.5.6. Notation matricielle#

  • Attention par defaut opération sur les éléments

  • les fonctions mathématiques dans numpy ont pour aguments des tableaux

  • np.dot produit scalaire

  • np.outer produit tensorielle

  • np.inner

X=np.arange(1,4,1)
print("X=",X)
print("X*X=",X*X)
print("X.X=",np.dot(X,X))
print("XoX=",np.outer(X,X))
print("XiX=",np.inner(X,X))

X= [1 2 3]
X*X= [1 4 9]
X.X= 14
XoX= [[1 2 3]
 [2 4 6]
 [3 6 9]]
XiX= 14

A=np.array(np.outer(np.arange(3),np.arange(3)))
print(type(A),A.shape)
print("A*X=\n",A*X)
print("A.X=\n",np.dot(A,X))
print("AoX=\n",np.outer(A,X))
print("AiA=\n",np.inner(A,A))
print("A.At=\n",np.dot(A,A.transpose()))

<class 'numpy.ndarray'> (3, 3)
A*X=
 [[ 0  0  0]
 [ 0  2  6]
 [ 0  4 12]]
A.X=
 [ 0  8 16]
AoX=
 [[ 0  0  0]
 [ 0  0  0]
 [ 0  0  0]
 [ 0  0  0]
 [ 1  2  3]
 [ 2  4  6]
 [ 0  0  0]
 [ 2  4  6]
 [ 4  8 12]]
AiA=
 [[ 0  0  0]
 [ 0  5 10]
 [ 0 10 20]]
A.At=
 [[ 0  0  0]
 [ 0  5 10]
 [ 0 10 20]]

3.3.5.7. attention:#

  • on évite les boucles explicites pour des questions d’efficacité

  • mais on commence toujours par écrire la forme explicite avec des boucles , puis ensuite la forme vectorielle

exemple: calcul de la forme quadratique $\( \Phi = \sum_{i=1}^n \sum_{j=1}^n A_{ij} X_i X_j - \sum_{j=1}^n B_j X_j\)$

# calcul explicite
Phi=0.0
n=X.size
B=np.ones(X.shape)
### BEGIN SOLUTION
for i in range(n):
    sum=0.0
    for j in range(n):
        sum = sum + A[i,j]*X[j]
    Phi = Phi + (sum - B[i])*X[i]
print(Phi)
### END SOLUTION

58.0

# fonction numpy
print(np.dot(np.dot(A,X)-B,X))

58.0

3.3.5.7.1. Question test#

%activity /usr/local/commun/ACTIVITY/IntroPython/questionAlgorithme2

%activity /usr/local/commun/ACTIVITY/IntroPython/questionAlgorithme3

3.3.6. Tracé avec matplotlib#

Pour tracer des courbes, nous utiliserons la bibliothèque matplotlib et son module pyplot. Sous Jupyter on utilise les instructions suivantes:

  %matplotlib inline
  import matplotlib.pyplot as plt

pour utiliser cette librairie avec le nom raccourci plt. La première instruction permet d’afficher les courbes dans le notebook (inline) plutôt que dans une fenêtre à part.

exemple

pour \(x\in[0,2]\), on veut tracer les courbes \(y_1=x^2\), \(y_2=x^3\) et \(y_3=\sqrt{x}\). Pour cela on crée un tableau X de valeurs entre 0 et 2, et on calcule ensuite les valeurs des courbes, puis on trace les 3 courbes avec des commandes du type

  plt.plot(X,Y1)

%matplotlib inline
import matplotlib.pyplot as plt

X  = np.linspace(0,2,41)
Y1 = X*X
Y2 = X**3
Y3 = np.sqrt(X)

3.3.6.1. tracé basique#

faire un tracé basique des 3 courbes dans la cellule suivante.

Attention ce genre de tracé n’est à utiliser que pour des tests et pas pour présenter des résultats, car les courbes n’ont pas de titre, les axes pas de label. Il faut regarder le code pour éventuellement comprendre.

N’utilisez jamais ce tracé basique pour présenter vos résultats !!!

# tracer basique

3.3.6.2. tracé de résultats#

Pour avoir un résultat de qualité, il faut ajouter un titre lisible, des labels avec les fonctions:

  • plt.title

  • plt.xlabel

  • plt.figure

  • plt.legend

# tracer avec des titres et des labels
# utilisation de taille de caractères plus grande
plt.rc('font', family='serif', size='18')
# tracer d'une figure plus grande
plt.figure(figsize=(10,8))
# plot x^2
plt.plot(X, Y1, color='r', linestyle='-', label='$x^2$')
# plot x^3
plt.plot(X, Y2, color='g', linestyle='--', label='$x^3$')
# plot sqrt(x)
plt.plot(X, Y3, color='b', linestyle=':',  label='$\sqrt{x}$')
# ajoute un titre et des labels 
plt.title('Courbes étudiées')
plt.xlabel('x')
plt.ylabel('y')
# ajoute la legende au meilleur endroit
plt.legend(loc='best');
../_images/e294b189f5d2d776f377965c4ceece0f7a4392d0589fb005ea0d5c04ac0945cb.png

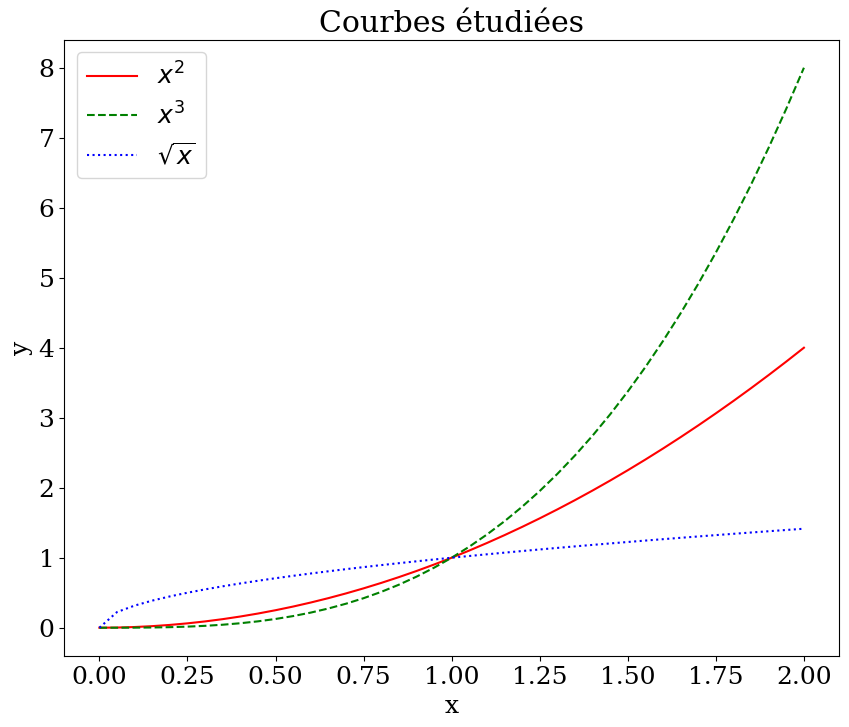
On a utiliser une notation \(\LaTeX\) pour afficher des expressions mathématiques: $x^2$ pour afficher \(x^2\) ou $\sqrt{x}$ pour afficher \(\sqrt{x}\).

Consulter le site de matplotlib https://matplotlib.org pour avoir un aperçu des immenses possibilités de tracé de matplotlib.

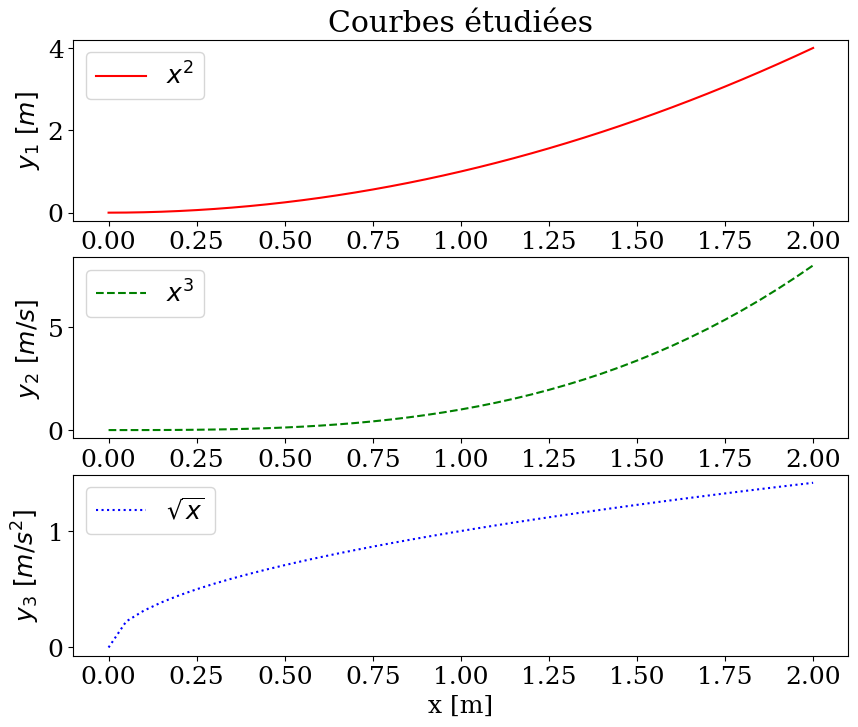
3.3.6.3. tracé avec des sous-figures#

# tracer de plusieurs sous figure
fig = plt.figure(figsize=(10,8))
# plot x^2
plt.subplot(3,1,1)
plt.plot(X, Y1, color='r', linestyle='-', label='$x^2$')
plt.title('Courbes étudiées')
plt.ylabel('$y_1$ $[m]$')
plt.legend(loc='best')
# plot x^3
plt.subplot(3,1,2)
plt.plot(X, Y2, color='g', linestyle='--', label='$x^3$')
plt.ylabel('$y_2$ $[m/s]$')
plt.legend(loc='best')
# plot sqrt(x)
plt.subplot(3,1,3)
plt.plot(X, Y3, color='b', linestyle=':',  label='$\sqrt{x}$')
# ajoute un titre et des labels 
plt.ylabel('$y_3$ $[m/s^2]$')
plt.xlabel('x [m]')
plt.legend(loc='best');
../_images/bba9de79cbcb20fcf08e1158852a3c139c08be12510e6a5f47f6ec86f5ba3a68.png

3.3.6.4. mise sur fichier#

  • fonction savefig()

attention: sauvegarde la figure dans une variable fig

fig.savefig(nom_fichier)

format pdf (vectoriel) ou image (png)

# sauvegarde de la figure
fig.savefig("mafig.png")
! ls -al mafig.png

-rw-rw-r-- 1 buffat buffat 63615 mars  19 16:43 mafig.png

3.3.6.5. Gallerie matplotlib#

from IPython.display import HTML
HTML('<iframe src=https://matplotlib.org/gallery.html width=800 height=500></iframe>')

/home/buffat/venvs/jupyter/lib/python3.10/site-packages/IPython/core/display.py:431: UserWarning: Consider using IPython.display.IFrame instead
  warnings.warn("Consider using IPython.display.IFrame instead")

3.3.7. Méthodologie#

  1. Réflexion algorithmique

  2. Création d’une bibliothèque de fonctions pour résoudre les sous-pbles:

     fichier mabib.py

  3. Utilisation d’un environnement de programmation (éditeur / jupyter lab/ shell)

  4. Validation de la bibliothèque

  5. Ecriture du programme principale en utilisant la bibliothéque

     import mabib.py

  6. Utilisation d’un notebook jupyter

  7. Analyse et validation du résultat (tracé de courbes)

  8. Ecriture d’un rapport au format \(\LaTeX\)

3.3.8. Bibliographie#

  • Python. The official Python web site.

  • Python tutorials. Le tutoriel officiel Python.

  • Think Python. “”How to Think Like a Computer Scientist”” by Allen B. Downey (free book).

  • COURS InProS Cours en vidéo d“« INtroduction à la Programmation Scientifique””

  • Scientific Python Le site officiel de SciPy, qui regroupe les bibliothèques scientifiques les plus utilisées en Python: numpy, scipy, matplotlib, sympy et pandas

3.3.9. FIN de la leçon#

Contenu