Modélisation d’un treillis en statique

Contenu

1.2. Modélisation d’un treillis en statique#

Marc BUFFAT, Département mécanique UCB Lyon 1 ../_images/treillisfig1.png

%matplotlib inline
# bibliothéque
import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
from matplotlib import rcParams
rcParams['font.family'] = 'serif'
rcParams['font.size'] = 14

1.2.1. Introduction#

On se propose d’étudier la modélisation d’un treillis par éléments finis.

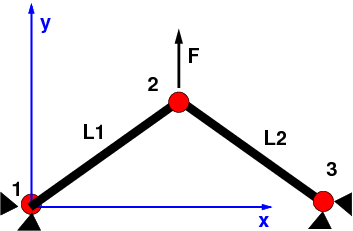
Le treillis étudié est un assemblage de poutres métalliques (voir figure) soumis à des efforts de traction compression ../_images/treillisfig1.png

### Modélisation du treillis

$N_e=2$ barres et $N_n=3$ noeuds
Assemblage des poutres: en statique système linéaire de dimension $2N_n = 6$ $$ K [u] = B $$
- $K$ matrice de rigidité $2N_n\times 2N_n$
- $[u]$ vecteur déplacements des noeuds $2N_n$

1.2.2. Structure de données#

Description du treillis de $N_e$ barres et $N_n$ noeuds:

tableau de coordonnées des noeuds X : vecteur $2N_n$
graphe du treillis (table de connection) G : tableau $(2,N_e)$
conditions aux limites de Dirichlet aux noeuds (code = type de CL)
numérotation à partir de 0 (convention python)

CL vecteur $N_n$ - 0 libre (pas de CL) - 1 déplacement nul suivant x - 2 déplacement nul suivant y - 3=1+2 déplacement nul suivant x et y

FCL tableau $N_n,2$ - composante de la force extérieure imposée au noeud

propriétés des barres: section, module d’Young, masse volumique

S, E, rho

# données brutes du problème
# ===================
# coordonnées des 3 nds
X = np.array([[0.0,0.0],[0.5,0.5],[1.0,0.0]])
# table de connection (numérotation naturelle à partir de 1)
Tbc = np.array([[1,2],[2,3]])
# parametres des barres en unité SI
E = 200.e9
S = 0.000025
rho = 8000
# Force appliquée en unité SI
F = 10000

1.2.3. Traitement des données#

A partir des données brutes, construire les données utiles pour la résolution du problème

numérotation python Tbc -> G
tableau des CL et des forces FCL

G = None
Nn = None
Ne = None
CL = None
FCL = None
### BEGIN SOLUTION
### END SOLUTION

1.2.4. Structure de données#

Regrouper tous les tableaux précédents dans une structure unique de type classe

 class Treillis():

approche générique
initialisation avec les tableaux génériques :
- table de connexion et coordonnées

# structure de donnees treillis: données table de connexion G et coordonnées de nds
class Treillis():
    def __init__(self,G,X):
        '''
           initialisation d un treillis a partir de la table de connexion G
           et des coordoonees X des noeuds. Attention: numérotation à partir de 0
        '''
        return

# utilisation: création du treillis, tableaux des CL et parametres 
tr = Treillis(G,X)
### BEGIN SOLUTION
### END SOLUTION

1.2.5. Affichage de la structure#

fonction print_treillis(tr,titre)
fonction trace_treillis(tr,titre)

def print_treillis(treillis,titre):
    '''affiche les informations du treillis avec un titre optionel'''

# vérification
print_treillis(tr,"mon treillis")

def trace_treillis(tr,titre):
    '''trace d un treillis tr avec un titre'''
    return

# vérification
trace_treillis(tr,"treillis initial")

1.2.6. Amélioration du tracé#

on souhaite améliorer la fonction précédente, en ajoutant la possibilité de tracer le numéro des noeuds.

utilisation d’un paramètre optionnel numero

def trace_treillis(tr,titre,numero=False):
    '''trace d un treillis tr avec un titre'''
    return

# vérification
trace_treillis(tr,"treillis initial",numero=True)

1.2.7. Algorithme#

structure de donnees: Treillis

initialisation des données du treillis
fonctions pour calculer des données nécessaires:
- longueur des barres,
- matrice de rotation (cosinus directeur)
assemblage de la matrice avec une boucles sur les barres
application des conditions aux limites
résolution du système linéaire
analyse du résultat

démarche

chaque partie correspond à l’écriture d’une fonction
on valide à chaque étape
validation de l’algorithme global sur un cas simple
application au cas étudié

1.2.8. Fonctions utiles#

bibliothéque treillis.py

longueur_treillis(tr) calcul des longueurs des barres
matrice_rotation(tr,l) calcul de matrice de rotation de la barre l

Soit $R$ la matrice de rotation:

\[\begin{split} \mathbf{R}=\left[\begin{array}{cc} \cos\alpha & \sin\alpha\\ -\sin\alpha & \cos\alpha \end{array}\right] \end{split}\]

la matrice de changement de repère $T$ s’écrit: $$ \mathbf{T=}\left[\begin{array}{cccc} R_{11} & R_{12} & 0 & 0\\ R_{21} & R_{22} & 0 & 0\\ 0 & 0 & R_{11} & R_{12}\\ 0 & 0 & R_{21} & R_{22} \end{array}\right] $$

def longueur_treillis(tr):
    """ calcul longueur des barres """
    # longueur des barres

# vérification
L = longueur_treillis(tr)
print("Longueur des barres L=",L)

# matrice de transfert T tq Ae = Tt.K.T
def matrice_rotation(tr,l):
    """ calcul matrice de transfert de l'element l (de 0 a ne-1) """

# vérification
T0 = matrice_rotation(tr,0)
print("T0=",T0)
T0 @ T0.transpose() 

1.2.9. Assemblage de la matrice#

Pour une barre le système $(4x4)$ s’écrit

\[\begin{split} \mathbf{T^{t}}\left[\begin{array}{cccc} K_{11} & 0 & K_{12} & 0\\ 0 & 0 & 0 & 0\\ K_{21} & 0 & K_{22} & 0\\ 0 & 0 & 0 & 0 \end{array}\right]\mathbf{T}\left[\begin{array}{c} u_{1x}\\ u_{1y}\\ u_{2x}\\ u_{2y}\end{array}\right] =\left[\begin{array}{c} F_{1x}\\ F_{1y}\\ F_{2x}\\ F_{2y} \end{array}\right] \end{split}\]

qu’il faut assembler dans un système global $2 N_n x N_n$

\[ A U = F \]

assemblage(tr) fonction d’assemblage pour le calcul de la matrice A (sans CL)

1.2.9.1. Algorithme assemblage#

 A matrice globale dimension (2nn,2nn)
 boucle sur les barres : k de 0 a ne-1    
     n1,n2 numéros des 2 sommets de la barre k
     2n1, 2n1+1, 2n2, 2n2+1  numéros des 4 ddl de la barre
     calcul de la matrice élémentaire (4*4) Ae = Tt K T
     ajout de la contribution Ae dans la matrice globale A:
         lignes 2n1,2n1+1,2n2,2n2+1  colonnes 2n1,2n1+1,2n2,2n2+1

# assemblage de la matrice globale
def assemblage(tr):
    """ assemblage de la matrice de rigidite"""
    # matrice de rigidite elementaire
    Ke=np.array([[1,0,-1,0],[0,0,0,0],[-1,0,1,0],[0,0,0,0]]);
    A=np.zeros((2*tr.nn,2*tr.nn));

# validation
# Assemblage de la matrice
A=assemblage(tr)
# verification A= At
print("Symétrie:",np.allclose(A,A.transpose()))
# somme des lignes
print("Somme des lignes:",np.sum(A,axis=1))
# déterminant
print("déterminant ",np.linalg.det(A))
#

1.2.10. Applications de CL#

sur la matrice A et le second membre B: - climites(tr,AA,BB) - si déplacement nul - met un 1 sur la diagonale, 0 sur la ligne et la colonne et dans B - forcage extérieure dans B

def climites(tr,AA,BB):
    '''imposition des CL dans la matrice A et des forces dans le 2nd membre B'''
    # attention on ne modifie pas les arguments mais on renvoie une nouvelle matrice A et B
    A = AA.copy()
    B = BB.copy()

# verification
# second membre
B=np.zeros((2*tr.nn))
# CLimites
A,B=climites(tr,A,B)
print("déterminant ",np.linalg.det(A))
print("B=\n",B)

1.2.11. Résolution#

utilisation de la bibliothèque linalg pour résoudre le système linéaire

fonction solve
transformation du vecteur solution $2*Nn$ en un tableau de déplacement $(Nn,2)$

# calcul de la solution
U=np.linalg.solve(A,B)
U=U.reshape((tr.nn,2))
print("Deplacement U=\n",U)
print("RDM: ",F/(E*S/L[0]))

1.2.12. Forces volumiques#

pour une poutre L suportant une largueur de toiture H avec masse par unité de surface $\rho$ $$ F = \rho g LH$$
répartition sur les 2 noeuds suivant force suivant y : $F/2$
charge supplémentaire du vent ou à la neige (attention direction)

\[p \approx \frac{1}{2} \rho_{air} Ue^2\]