Notebook: Application à l’étude d’une TurboVoile

2.3. Notebook: Application à l’étude d’une TurboVoile#

Marc BUFFAT, département mécanique, UCB Lyon 1

../../_images/turbo-voile.jpg 
import sympy as sp
import numpy as np
import matplotlib.pyplot as plt

2.3.1. Analyse et paramètres du problème#

  • \(U_0\) vitesse relative du vent d’angle \(\beta\)

  • \(V_b\) vitesse du bateau

  • \(R\) rayon du cylindre

  • \(H\) hauteur du cylindre

  • \(\omega\) vitesse de rotation

  • \(C_f\) coefficient de traînée du bateau ,\(S_m\) surface mouillée

  • \(\rho_0\) masse volumique de l’air et \(\rho\) masse volumique de l’eau

  • \(Fp\) force de portance

  • \(Ft\) force de traînée

# parametres du problème
Cf, U0, R, H, omega, rho0, rho, L = sp.symbols('C_f U_0 R H omega rho_0 rho L',positive=True)

2.3.2. Modèle fluide parfait: solution analytique#

  • cylindre rayon R et de longueur L

  • solution potentiel

2.3.2.1. Solution potentiel autour cylindre#

  • solution sans rotation

\[ \psi_1 = U_0 r \sin\theta - U_0\frac{R^2\sin\theta}{r}\]

  • vortex de circulation \(\Gamma\)

\[ \psi_2 = \frac{\Gamma}{2\pi} \ln r \]

solution de l’équation de Laplace

\[\Delta \psi = 0\]

Le champ de vitesse est obtenu par

\[ U_r = \frac{1}{r} \frac{\partial \Psi}{\partial \theta} \mbox{ et } U_\theta = -\frac{\partial \Psi}{\partial r} \]

et

\[ U_x = U_r \cos\theta - U_\theta \sin \theta \mbox{ et } U_y = U_r \sin\theta + U_\theta \cos \theta\]

Détermination de la relation entre l’angle du point d’arrêt et la circulation.

# calcul de la circulation en fct de omega
Gamma = 2*sp.pi*R*omega*R
display("Circulation Gamma",Gamma)

'Circulation Gamma'
\[\displaystyle 2 \pi R^{2} \omega\]
r,theta = sp.symbols('r theta')
psi1 = U0*r*sp.sin(theta) - U0*R**2*sp.sin(theta)/r
psi2 = Gamma/(2*sp.pi)*sp.log(r)
display("psi = ",psi1+psi2)

'psi = '
\[\displaystyle - \frac{R^{2} U_{0} \sin{\left(\theta \right)}}{r} + R^{2} \omega \log{\left(r \right)} + U_{0} r \sin{\left(\theta \right)}\]
Ut1 = -psi1.diff(r).subs(r,R)
Ut2 = -psi2.diff(r).subs(r,R)
Ut = Ut1 + Ut2
display("cdt arret Ut=0 soit ",Ut,"=0")

'cdt arret Ut=0 soit '
\[\displaystyle - R \omega - 2 U_{0} \sin{\left(\theta \right)}\]
'=0'

# condition au pt d'arret -> theta en fct de omega
display("Ut=",Ut)
Theta=sp.solve(Ut,theta)[1]
display(sp.Eq(theta,Theta))

'Ut='
\[\displaystyle - R \omega - 2 U_{0} \sin{\left(\theta \right)}\]
\[\displaystyle \theta = - \operatorname{asin}{\left(\frac{R \omega}{2 U_{0}} \right)}\]

  • Condition au pt d’arrêt sur le cylindre: \(\theta\) < 20 degré (analogie profil d’aile)

  • d’où la vitesse de rotation max du cylindre avec \(\sin\theta \approx \theta\)

# w_max
theta_m = sp.symbols('theta_m')
omega_m = theta_m*2*U0/R
display("omega max:",omega_m)

'omega max:'
\[\displaystyle \frac{2 U_{0} \theta_{m}}{R}\]

2.3.2.2. Force de portance#

la force de portance pour un cylindre de rayon R et de longueur L est avec ce modèle proportionnelle à la circulation de vitesse \(\Gamma\)

L’analyse dimensionnelle donne

Fp = rho0*U0*Gamma*L
display("Force de portance ",Fp)

'Force de portance '
\[\displaystyle 2 \pi L R^{2} U_{0} \omega \rho_{0}\]

2.3.3. Analyse du calcul comsol#

  • simulation pour différentes valeurs de \(\theta_1\)

  • calcul répartition de pression autour du cylindre

  • analyse des résultats

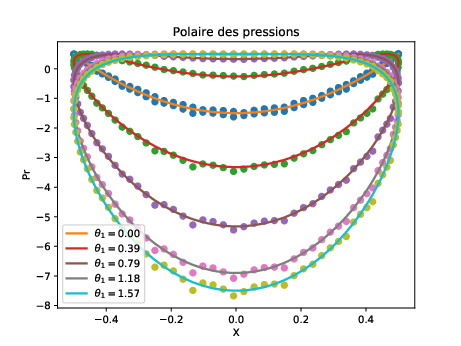
polaire

  • calcul portance

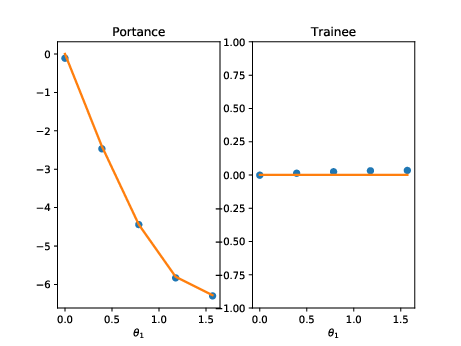
portance

  • calcul circulation

d’où la loi \(F_p = F(\Gamma)\)

  • calcul de la vitesse de rotation \( \omega\)

\[\Gamma = 2 \pi R \omega R\]

2.3.4. Bilan des forces#

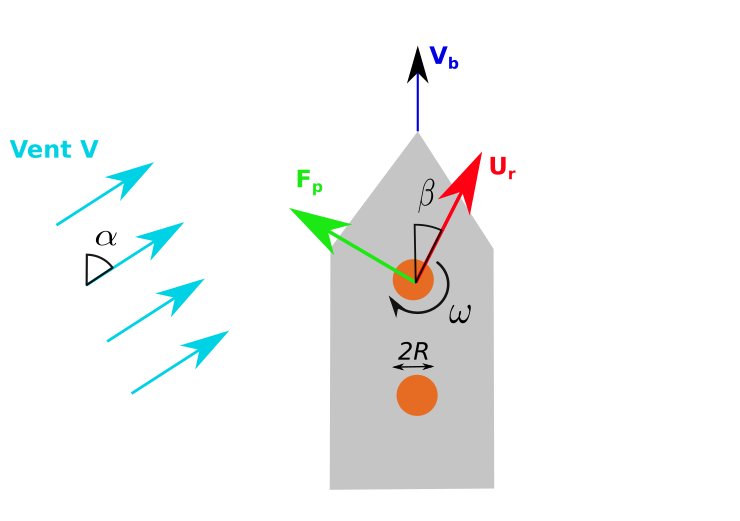
turbo_voile

Calcul dans le référentiel du bateau

  • \(U_r\) = vitesse du vent / bateau (correspond à \(U_0\))

  • \(V_b\) = vitesse absolue du bateau

  • \(V \) = vitesse absolue du vent d’angle \(\alpha\) / \(V_b\)

  • \(\beta\) = angle d’incidente de U0 dans le repère lié au bateau

Pour les forces :

  1. la force de portance = fonction de Ur et \(\beta\)

  2. la force de trainée = fonction de Vb

Analyse dimensionnelle

  • force de portance $\( F_p = F_p(\rho,\omega,U_0,R,H)\)$

  • force de traînée (surface mouillée du bateau) $\( F_t = F_t(\rho,C_f,V_b,S_m)\)$

# Force de portance
Fp = rho0*U0*Gamma*H
display("Portance: Fp=",Fp)

'Portance: Fp='
\[\displaystyle 2 \pi H R^{2} U_{0} \omega \rho_{0}\]
# alpha:angle du vent, V vitesse vent, Vb vitesse bateaux 
Cf, alpha = sp.symbols('C_f alpha')
V, Vb = sp.symbols('V V_b')

# angle beta de la vitesse relative
beta = sp.atan2(V*sp.sin(alpha),V*sp.cos(alpha)+Vb)
display("Angle du vent: beta =",beta)

'Angle du vent: beta ='
\[\displaystyle \operatorname{atan}_{2}{\left(V \sin{\left(\alpha \right)},V \cos{\left(\alpha \right)} + V_{b} \right)}\]
# module vitesse relative
Ur = sp.sqrt((V*sp.sin(alpha))**2+(V*sp.cos(alpha)+Vb)**2)
display("Vitesse relative du vent: Ur =",Ur)

'Vitesse relative du vent: Ur ='
\[\displaystyle \sqrt{V^{2} \sin^{2}{\left(\alpha \right)} + \left(V \cos{\left(\alpha \right)} + V_{b}\right)^{2}}\]
display("Angle de la force de portance:",sp.cos(sp.pi/2-beta))

'Angle de la force de portance:'
\[\displaystyle \frac{V \sin{\left(\alpha \right)}}{\sqrt{V^{2} \sin^{2}{\left(\alpha \right)} + \left(V \cos{\left(\alpha \right)} + V_{b}\right)^{2}}}\]
# d'où la force motrice
Fm = sp.cos(sp.pi/2-beta)*Fp.subs({U0:Ur})
display("Force motrice Fm=",Fm)

'Force motrice Fm='
\[\displaystyle 2 \pi H R^{2} V \omega \rho_{0} \sin{\left(\alpha \right)}\]
# force de trainee fonction de la surface mouillée S
S = sp.symbols('S')
Ft = rho*Cf*Vb**2*S/2
display("Force de trainée: Ft=",Ft)

'Force de trainée: Ft='
\[\displaystyle \frac{C_{f} S V_{b}^{2} \rho}{2}\]

2.3.5. Equilibre des forces pour un nbre de cylindres Nc#

On suppose que le bateau n’a pas d’autre moyens de propulsion que la turbovoile

  1. Bilan des forces => portance + trainée = 0

  2. Calcul de la surface mouillée S du bateau (pour la trainée)

  3. Loi de la vitesse V en fonction de omega

# cas avec Nc cylindres
Nc = sp.symbols('N_c')
eq1 = sp.Eq(Nc*Fm,Ft)
display("Equilibre du bateau ",eq1)

'Equilibre du bateau '
\[\displaystyle 2 \pi H N_{c} R^{2} V \omega \rho_{0} \sin{\left(\alpha \right)} = \frac{C_{f} S V_{b}^{2} \rho}{2}\]
# taille du bateau L longeur , La largueur, h tirant d'eau
L, La, h = sp.symbols('L L_a h')
Sm = L*sp.sqrt(La**2+4*h**2)
# surface mouillée
display("Surface mouillée ",Sm)
eq3 = eq1.subs({S:Sm})
# equilibre => Vb en fonction de omega
display("Equilibre du bateau:",eq3)

'Surface mouillée '
\[\displaystyle L \sqrt{L_{a}^{2} + 4 h^{2}}\]
'Equilibre du bateau:'
\[\displaystyle 2 \pi H N_{c} R^{2} V \omega \rho_{0} \sin{\left(\alpha \right)} = \frac{C_{f} L V_{b}^{2} \rho \sqrt{L_{a}^{2} + 4 h^{2}}}{2}\]

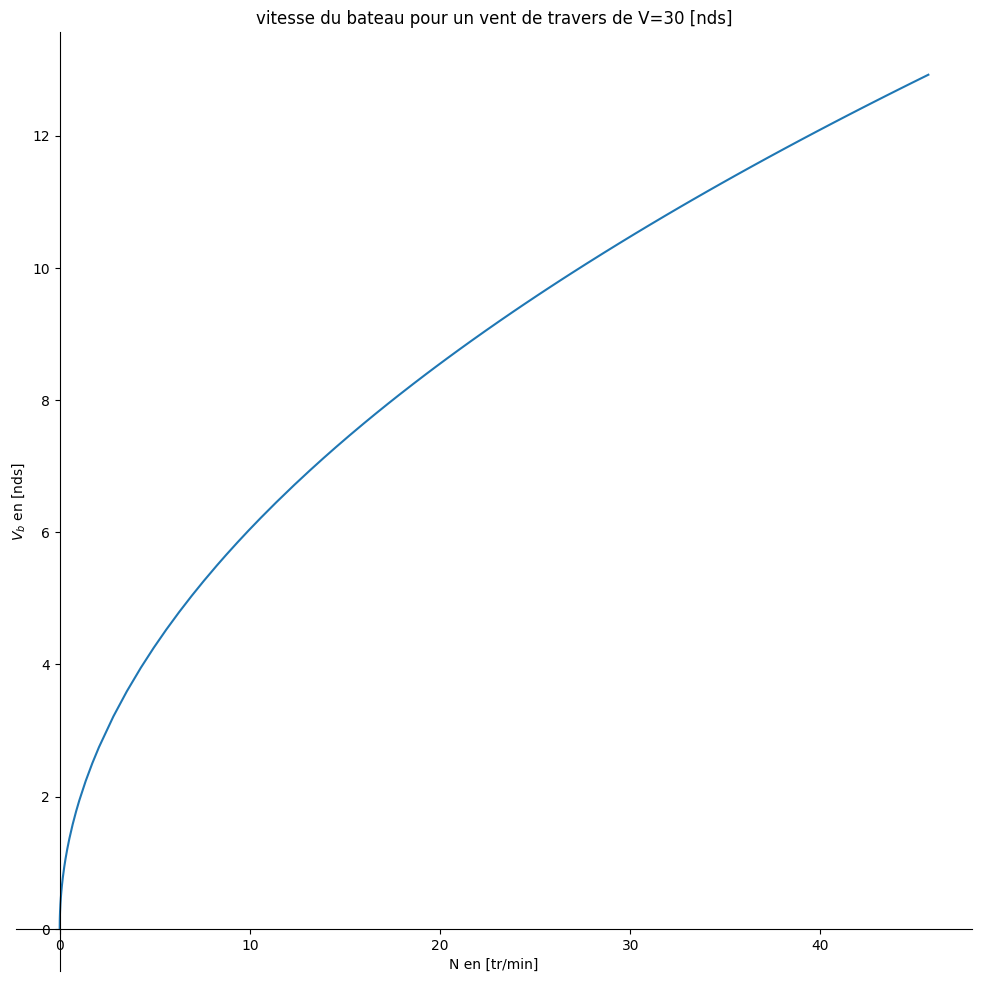
2.3.6. Application numérique#

  • conteneur Enercon L=130 m x La=22.5 m avec h~5 m tirant d’eau

  • vent V=30 nds (x 1.85 km/h) de travers (\(\alpha = \pi/2\))

  • Nc=4 cylindres

  • hauteur cylindre H = 2*h

  • diametre La/5

  • ordre de grandeur trainee CF=0.00133

  • \(\theta_m\)=20 degrés

# parametres
vals = { theta_m:20*np.pi/180, Nc:4, V:30*1.85*1000/3600, H:2*h, R:La/10, Cf:0.00133, alpha:sp.pi/2 , L:130, La:22.5, h:5, 
         rho0:1, rho:1000, sp.pi:np.pi }
# vitesse de rotation en tr/min
N = sp.symbols("N")
# rotation max
Wmax = omega_m.subs(vals).subs({U0:Ur,Vb:0}).subs(vals)
print('omega_max=',Wmax,' N_max=',Wmax*60/(2*np.pi)," tr/min")
# vitesse bateau fct de omega
eq4=eq3.subs(vals).subs(vals).subs(omega,N*2*sp.pi/60)
display("Equation d'équilibre ",eq4)
# vitesse bateau en nds
VB=sp.solve(eq4,Vb)[1]*3600/1000/1.85
display("Vitesse du bateau en nds",sp.Eq(Vb,VB))

omega_max= 4.78349498694742  N_max= 45.6790123456790  tr/min

"Equation d'équilibre "
\[\displaystyle 653.843971028376 \pi N = 2128.58439241318 V_{b}^{2}\]
'Vitesse du bateau en nds'
\[\displaystyle V_{b} = 1.91160137298645 \sqrt{N}\]
plt.rcParams['figure.figsize'] = 10, 10
sp.plot(VB,(N,0,Wmax*60/(2*np.pi)),title="vitesse du bateau pour un vent de travers de V=30 [nds]",
        xlabel="N en [tr/min]",ylabel="$V_b$ en [nds]",lw=4);
../../_images/1ab41b23b4d1cab82a4ee3459a7f02788b7504da900afe49bb1b10a05a9ec54e.png

2.3.7. Analyse paramétrique#

On calcule la taille de la turbovoile en fonction de la taille du bateau L variant de 80 a 200m

N = 5
LL = np.linspace(80,200,N)
for i in range(N):
    # parametres
    vals = { theta_m:20*np.pi/180, Nc:1, V:60*1.85*1000/3600, H:2*h, R:La/10, Cf:0.00133, alpha:sp.pi/2 , 
            La:22.5*LL[i]/130, h:5*LL[i]/130, L:LL[i], rho0:1, rho:1000, sp.pi:np.pi }
    # rotation max
    Wmax = omega_m.subs(vals).subs({U0:Ur,Vb:0}).subs(vals)
    # vitesse bateau fct de omega
    eq4=eq3.subs(vals).subs(vals).subs({omega:Wmax})
    # vitesse bateau en nds
    VB=sp.solve(eq4,Vb)[1]*3600/1000/1.85
    #
    val = []
    for p in [L,La,h,R]:
        val.append(p.subs(vals).subs(vals))
    # 
    print("L={:.1f}\t turbovoile  La={:.1f} h={:.1f} R={:.1f} wmax={:.1f} \t vitesse Vb={:.1f} [nds]".
          format(val[0],val[1],val[2],val[3],Wmax,VB))

L=80.0	 turbovoile  La=13.8 h=3.1 R=1.4 wmax=15.5 	 vitesse Vb=12.9 [nds]
L=110.0	 turbovoile  La=19.0 h=4.2 R=1.9 wmax=11.3 	 vitesse Vb=12.9 [nds]
L=140.0	 turbovoile  La=24.2 h=5.4 R=2.4 wmax=8.9 	 vitesse Vb=12.9 [nds]

L=170.0	 turbovoile  La=29.4 h=6.5 R=2.9 wmax=7.3 	 vitesse Vb=12.9 [nds]
L=200.0	 turbovoile  La=34.6 h=7.7 R=3.5 wmax=6.2 	 vitesse Vb=12.9 [nds]

2.3.8. The END#

Contenu