Modélisation d’un treillis par éléments finis

1.1. Modélisation d’un treillis par éléments finis#

1.1.1. Introduction#

On se propose d’étudier la modélisation d’un treillis par éléments finis. Un treillis est un assemblage de poutres métalliques (voir figure ci-dessous).

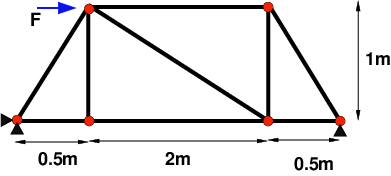
Treillis

On suppose que l’assemblage subit uniquement des efforts de compression (ou extension) sans effet de flexion.

1.1.2. Etude d’une poutre seule#

Pour une poutre de longueur L , de coefficient d’élasticité E et de section S, l’équation d’équilibre statique s’écrit (en notant \(u(x)\) le déplacement)

\[\frac{\partial}{\partial x}(ES\frac{\partial u}{\partial x})=0\]

A cette équation, il faut ajouter 2 conditions aux limites:

  1. soit des conditions d’encastrement (condition de Dirichlet):
    \(u=0\)

  2. soit des conditions de force imposée (condition de Neuman):
    \(ES\frac{\partial u}{\partial x}=F\)

Dans la suite on supposera que l’on impose 2 conditions de force en \(x=0\) et \(x=l\).

1.1.2.1. Formulation éléments finis#

Soit \(\delta u\) un déplacement virtuel licite (i.e. vérifiant les C.L. de Dirichlet), la formulation faible s’écrit:

\[ \underbrace{\int_{0}^{l}ES\frac{\partial u}{\partial x}\frac{\partial\delta u}{\partial x}dx}_{\mbox{travail des forces internes}} =\underbrace{F_{2}\delta u(l)-F_{1}\delta u(0)}_{\mbox{travail des forces extérieures}} \]

On cherche une solution approchée \(u^{h}\) en utilisant une approximation avec des éléments finis \(P^{1}\) sur un maillage d’un seul élément \(e_{1}=[0,l]\)

\[u^{h}(x)=u_{1}\Phi_{1}(x)+u_{2}\Phi_{2}(x)\]

où \(\Phi_{1}(x)\) et \(\Phi_{2}(x)\) sont les fonctions base associées aux deux noeuds du maillage \(P_{1}(x=0)\) et \(P_{2}(x=l)\)

La formulation Galerkin s’écrit, en prenant pour fonction test \(\delta u^{h}\), les fonctions de base \(\Phi_{1}(x)\) et \(\Phi_{2}(x)\) :

\[\begin{split}\begin{aligned} u_{1}\int_{0}^{l}ES\frac{\partial\Phi_{1}}{\partial x}\frac{\partial\Phi_{1}}{\partial x}dx+u_{2}\int_{0}^{l}ES\frac{\partial\Phi_{2}}{\partial x}\frac{\partial\Phi_{1}}{\partial x}dx & = & -F_{1}\\ u_{1}\int_{0}^{l}ES\frac{\partial\Phi_{1}}{\partial x}\frac{\partial\Phi_{2}}{\partial x}dx+u_{2}\int_{0}^{l}ES\frac{\partial\Phi_{2}}{\partial x}\frac{\partial\Phi_{2}}{\partial x}dx & = & +F_{2} \end{aligned}\end{split}\]

c’est un système linéaire 2x2

\[\begin{split}\mathbf{K}\left[\begin{array}{c} u_{1}\\ u_{2} \end{array}\right]=\mathbf{B}\end{split}\]

\(\mathbf{K}\) est la matrice de rigidité qui vaut pour des éléments \(P^{1}\) de longueur \(h\)

\[\begin{split}\mathbf{K}=\frac{ES}{h}\left[\begin{array}{cc} 1 & -1\\ -1 & 1 \end{array}\right]\,\end{split}\]

1.1.2.2. Cas d’une poutre incliné d’un angle \(\alpha\)#

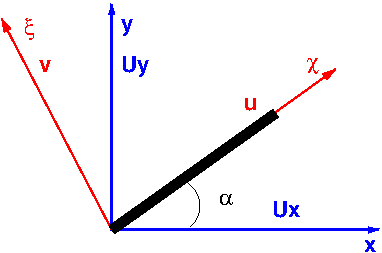
poutre

Dans les axes \((\chi,\xi)\) liés à la barre, le déplacement \(u\) est donné par les équations précédentes et le déplacement \(v\) n’est associé à aucune équation. Le système linéaire sur \(u\) et \(v\) s’écrit:

\[\begin{split}\left[\begin{array}{cccc} K_{11} & 0 & K_{12} & 0\\ 0 & 0 & 0 & 0\\ K_{21} & 0 & K_{22} & 0\\ 0 & 0 & 0 & 0 \end{array}\right]\left[\begin{array}{c} u_{1}\\ v_{1}\\ u_{2}\\ v_{2} \end{array}\right]=\left[\begin{array}{c} -F_{1}\\ 0\\ F_{2}\\ 0 \end{array}\right]\end{split}\]

Pour passer dans le repère fixe, il faut introduire la matrice de changement de repère:

\[\begin{split}\mathbf{R}=\left[\begin{array}{cc} \cos\alpha & \sin\alpha\\ -\sin\alpha & \cos\alpha \end{array}\right]\end{split}\]

ce qui permet d’écrire le déplacement dans \((\chi,\xi)\) en fonction du déplacement dans \((x,y)\)

\[\begin{split}\left[\begin{array}{c} u_{1}\\ v_{1}\\ u_{2}\\ v_{2} \end{array}\right]=\mathbf{T}\left[\begin{array}{c} u_{1x}\\ u_{1y}\\ u_{2x}\\ u_{2y} \end{array}\right]\,\,\mbox{avec\,}\,\,\mathbf{T=}\left[\begin{array}{cccc} R_{11} & R_{12} & 0 & 0\\ R_{21} & R_{22} & 0 & 0\\ 0 & 0 & R_{11} & R_{12}\\ 0 & 0 & R_{21} & R_{22} \end{array}\right]\end{split}\]

et de projeter les forces de \((\chi,\xi)\) dans \((x,y)\)

\[\begin{split}\left[\begin{array}{c} F_{x1}\\ F_{y1}\\ F_{x2}\\ F_{y2} \end{array}\right]=\mathbf{T^{t}}\left[\begin{array}{c} F_{1}\\ 0\\ F_{2}\\ 0 \end{array}\right]\,\end{split}\]

ce qui conduit au système linéaire dans \((x,y)\)

\[\begin{split}\mathbf{T^{t}}\left[\begin{array}{cccc} K_{11} & 0 & K_{12} & 0\\ 0 & 0 & 0 & 0\\ K_{21} & 0 & K_{22} & 0\\ 0 & 0 & 0 & 0 \end{array}\right]\mathbf{T}\left[\begin{array}{c} u_{1x}\\ u_{1y}\\ u_{2x}\\ u_{2y} \end{array}\right]=\left[\begin{array}{c} F_{1x}\\ F_{1y}\\ F_{2x}\\ F_{2y} \end{array}\right]\end{split}\]

1.1.3. BE étude du treillis#

Un treillis est un assemblage de \(Ne\) poutres reliées en \(Nn\) noeuds. On veut déterminer les déplacements \((u_{x},u_{y})\) de chaque noeuds, ainsi que les contraintes dans les poutres.

1.1.3.1. étude statique#

Le modèle discret consiste à écrire le système linéaire

\[\mathcal{K}U=\mathcal{B}\]

où \(U\) est le vecteur déplacement de \((2\,Nn)\) réels, et \(\mathcal{K}\) la matrice de rigidité et \(\mathcal{B}\) le second membre (forces appliquées)

1.1.3.1.1. Algorithme:#

  1. Assemblage de la matrice \(\mathcal{K}\) (boucle sur les barres)

  2. Calcul du second membre \(\mathcal{B}\) (forces appliquées)

  3. Conditions aux limites (Dirichlet, Neuman)

  4. Résolution du système linaire

1.1.3.1.2. Structure de données#

Description du treillis de \(Ne\) barres et \(Nn\) noeuds:

  • tableau de coordonnées des noeuds \(X\) vecteur \((2Nn)\) réels

  • graphe du treillis (table de connection) \(G\) tableau \((2,Ne)\) entiers

  • conditions aux limites aux noeuds \(CL\) tableau \((Nn)\) entiers
    (code = type de CL 0 rien, 1 u=0, 2 v=0, 3 u,v=0, 4 Fe)

  • Forces extérieures \(Fe\) tableau \(2Nn\) réels

1.1.3.1.3. Implémentation en python#

utilisation de numpy et de structure (classe)

  • vecteur réel
    X=array([0.2,0.3,0.5])
    X=array([0.2,0.3,0.5],dtype=float)

  • vecteur entier
    I=array([1,3,4],dtype=int)

  • matrice
    A=array([[1,2],[3,4]])

  • concatenation
    concatenate((A,B))
    concatenate((A,B),axis=1)
    hstack((A,B))
    vstack((A,B))
    vstack((hstack((A,B)),hstack((B,A))))

  • manipulation
    transpose(A)

  • adressage indirecte
    A[ix_([1,0],[2,1])]

  • resolution système lineaire
    linalg.solve(A,B)

  • valeurs propres
    D,V=linalg.eig(A)

  • inverse
    linalg.inv(A)

1.1.3.2. étude dynamique#

Pour une poutre de longueur L , de coefficient d’élasticité E et de section S, l’équation d’équilibre dynamique s’écrit (en notant \(u(x,t)\) le déplacement)

\[\rho S\frac{\partial^{2}u}{\partial t^{2}}=\frac{\partial}{\partial x}(SE\frac{\partial u}{\partial x})\]

Matrice élémentaire de masse

\[\begin{split}M=\rho SL\left[\begin{array}{cc} \frac{1}{3} & \frac{1}{6}\\ \frac{1}{6} & \frac{1}{3} \end{array}\right]\end{split}\]
\[\begin{split}\mathcal{M}_{e}=\left[\begin{array}{cccc} M_{11} & 0 & M_{12} & 0\\ 0 & 0 & 0 & 0\\ M_{21} & 0 & M_{22} & 0\\ 0 & 0 & 0 & 0 \end{array}\right]\end{split}\]

Pour le treillis, en vibration libre, on doit résoudre le système d’EDO linéaire:

\[\mathcal{M}\ddot{U}=\mathcal{K}U\]

Ce qui conduit à un problème aux valeurs propres pour la matrice \(A\):

\[A\Lambda=\lambda\Lambda\mbox{ avec }A=\mathcal{M}^{-1}\mathcal{K}\]
Contenu