Table des matières
1.4. Modélisation d’une ferme de toiture industrielle (treillis)#

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
1.4.1. Modélisation d’une ferme (treillis de toiture)#
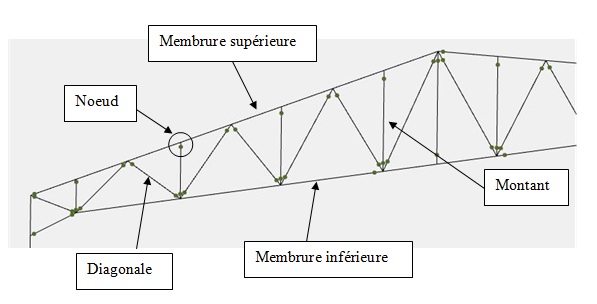
Les fermes à treillis sont composés de barres fines: il s’agit de diagonales et de montants rejoignant la membrure inférieure (appelée aussi entrait) et la membrure supérieure (appelée aussi arbalétrier). Le tout formant un système triangulé, très efficace (maximum de résistance pour minimum de poids), mais coûteux en main d’oeuvre.
Elles peuvent reposer soit sur des poteaux (ce qui est le cas dans la modélisation ci-dessus), soit être prises entre 2 murs.
Les barres sont reliées entre elles aux extrémités (noeuds), qu’on considère en général articulées. Ce n’est pas forcément le cas, mais c’est l’hypothèse de calcul usuelle qui permet de surestimer légèrement les efforts. Dans la réalité, les assemblages (boulons, rivets, soudures) sont des encastrements partiels.
Si toutes les charges s’appliquent au niveau des noeuds, les barres travaillent uniquement en traction/compression, aucune flexion n’existe : c’est le cas habituel.
Il arrive cependant que les charges ne soient pas forcément appliquées au niveau des noeuds : par exemple si la couverture est posée directement sur la membure supérieure (donc sans l’intermédiaire de pannes), ou si les pannes sont posées entre les noeuds de la membrure supérieure. Dans ce cas se rajoutent des termes de flexion à prendre en compte dans les calculs.
1.4.1.1. structure de toiture industrielle#
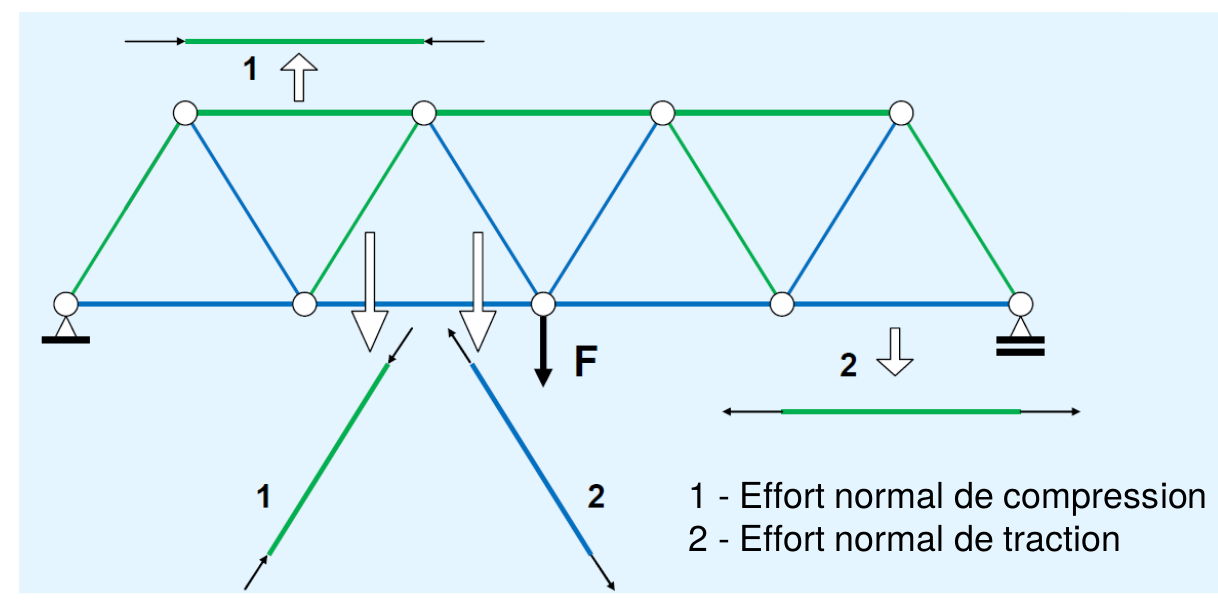
ferme à treillis: système de barres attachées aux noeuds (2D)
hypothèse: efforts principaux sont des efforts normaux.
les charges sont appliquées aux noeuds
Si les attaches aux nœuds sont rigides, cela introduit des efforts de flexion secondaires
1.4.1.2. conditions d’utilisation#
Utilisation de treillis dans les bâtiments à simple rez-de-chaussée
Pour supporter les charges de toiture :
charges gravitaires (poids propre, charge de neige, couverture)
équipements disposés, soit sur le toit, soit suspendus à la structure
actions dues au vent
1.4.1.3. modèle simplifié#
treillis en 2D
étude en traction/compression
effets des charges gravitaires
effet du vent
1.4.2. Génération des treillis#
1.4.2.1. différents type de treillis#
1.4.2.2. parametres:(lien )#
# structure de donnees treillis
class Treillis():
def __init__(self):
# ptes par neuds
self.nn = 0
self.X = None
# ptes par barre
self.ne = 0
self.G = None
return
def symmetrie(self,L):
"""symmetrisation / a x=L"""
T=Treillis()
T.nn = self.nn
T.X = np.copy(self.X)
T.ne = self.ne
T.G = np.copy(self.G)
T.X[:,0] = 2*L - T.X[:,0]
return T
def trace(self):
plt.plot(self.X[:,0],self.X[:,1],'or')
for k in range(self.ne):
n1 = self.G[k,0]
n2 = self.G[k,1]
plt.plot([self.X[n1,0],self.X[n2,0]],[self.X[n1,1],self.X[n2,1]],'-b')
plt.text((self.X[n1,0]+self.X[n2,0])/2,(self.X[n1,1]+self.X[n2,1])/2,str(k),color='b',fontsize=16)
for i in range(self.nn):
plt.text(self.X[i,0],self.X[i,1],str(i),color='r',fontsize=18)
plt.axis('equal')
return
def write(self,nom):
F = open(nom,"w")
F.write("# treillis {}\n".format(nom))
F.write("%d %d\n"%(self.ne,self.nn))
F.write("# coordonnees des noeuds\n")
for i in range(self.nn):
F.write("%f %f\n"%(self.X[i,0],self.X[i,1]))
F.write("# barres du treillis\n")
for k in range(self.ne):
F.write("%d %d\n"%(self.G[k,0],self.G[k,1]))
F.close()
return
def treillis1(n,L,H):
"""treillis type 1"""
T = Treillis()
T.nn = 2*n - 1
T.X = np.zeros((T.nn,2),dtype=float)
T.ne = 3*(n-1)
T.G = np.zeros((T.ne,2),dtype=int)
for i in range(n):
T.X[i,0] = i*L/(n-1)
T.X[i,1] = 0.
for i in range(n-1):
T.X[n+i,0] = (n-i-1)*L/(n-1)
T.X[n+i,1] = (n-i-1)*H/(n-1)
for k in range(n-1):
T.G[k,:] = [k,k+1]
T.G[k+n-1,:] = [n+k,n+k+1]
if k == n-2:
T.G[k+n-1,1 ] = 0
T.G[k+2*n-2,:] = [k+1,2*n-2-k]
return T
#
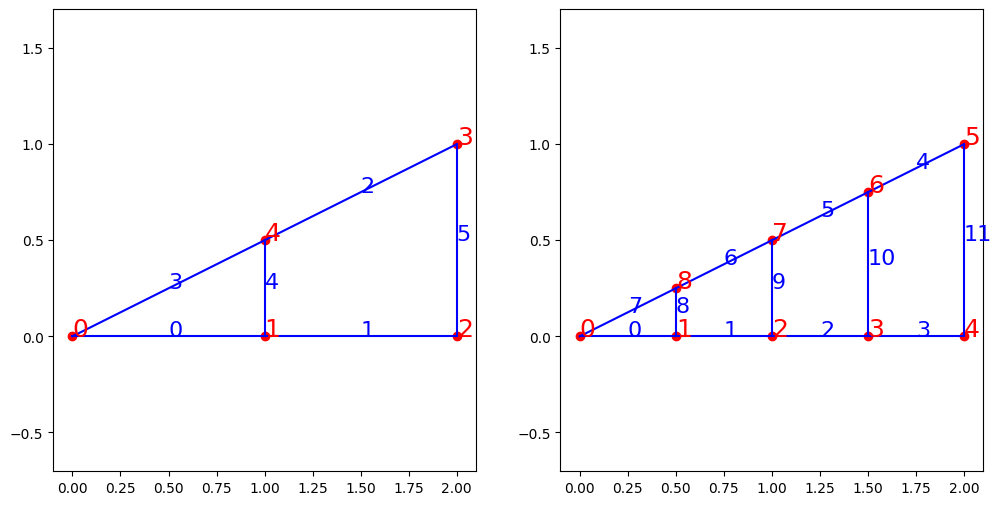
plt.figure(figsize=(12,6))
plt.subplot(1,2,1)
T1 = treillis1(3,2.,1.)
T1.trace()
plt.subplot(1,2,2)
T2 = treillis1(5,2.,1.)
T2.trace()
def treillis1a(n,L,H):
"""treillis type 1 variante 1"""
T = Treillis()
T.nn = 2*n - 1
T.X = np.zeros((T.nn,2),dtype=float)
T.ne = 3*(n-1) + (n-2)
T.G = np.zeros((T.ne,2),dtype=int)
for i in range(n):
T.X[i,0] = i*L/(n-1)
T.X[i,1] = 0.
for i in range(n-1):
T.X[n+i,0] = (n-i-1)*L/(n-1)
T.X[n+i,1] = (n-i-1)*H/(n-1)
for k in range(n-1):
T.G[k,:] = [k,k+1]
T.G[k+n-1,:] = [n+k,n+k+1]
if k == n-2:
T.G[k+n-1,1 ] = 0
T.G[k+2*n-2,:] = [k+1,2*n-2-k]
k0 = 3*n-3
for k in range(n-2):
T.G[k+k0,:]= [k+1,2*n-2-k-1]
return T
#
plt.figure(figsize=(12,6))
plt.subplot(1,2,1)
T1 = treillis1a(3,2.,1.)
T1.trace()
plt.subplot(1,2,2)
T2 = treillis1a(5,2.,1.)
T2.trace()
def treillis1b(n,L,H):
"""treillis type 1 variante 2"""
T = Treillis()
T.nn = 2*n - 1
T.X = np.zeros((T.nn,2),dtype=float)
T.ne = 3*(n-1) + (n-2)
T.G = np.zeros((T.ne,2),dtype=int)
for i in range(n):
T.X[i,0] = i*L/(n-1)
T.X[i,1] = 0.
for i in range(n-1):
T.X[n+i,0] = (n-i-1)*L/(n-1)
T.X[n+i,1] = (n-i-1)*H/(n-1)
for k in range(n-1):
T.G[k,:] = [k,k+1]
T.G[k+n-1,:] = [n+k,n+k+1]
if k == n-2:
T.G[k+n-1,1 ] = 0
T.G[k+2*n-2,:] = [k+1,2*n-2-k]
k0 = 3*n-3
for k in range(n-2):
T.G[k+k0,:]= [k+2,2*n-2-k]
return T
#
plt.figure(figsize=(12,6))
plt.subplot(1,2,1)
T1 = treillis1b(3,2.,1.)
T1.trace()
plt.subplot(1,2,2)
T2 = treillis1b(5,2.,1.)
T2.trace()
def treillis1c(n,L,H):
"""treillis type 1 variante 3"""
T = Treillis()
T.nn = 2*n - 1
T.X = np.zeros((T.nn,2),dtype=float)
T.ne = 3*(n-1) + 2*(n-2)
T.G = np.zeros((T.ne,2),dtype=int)
for i in range(n):
T.X[i,0] = i*L/(n-1)
T.X[i,1] = 0.
for i in range(n-1):
T.X[n+i,0] = (n-i-1)*L/(n-1)
T.X[n+i,1] = (n-i-1)*H/(n-1)
for k in range(n-1):
T.G[k,:] = [k,k+1]
T.G[k+n-1,:] = [n+k,n+k+1]
if k == n-2:
T.G[k+n-1,1 ] = 0
T.G[k+2*n-2,:] = [k+1,2*n-2-k]
k0 = 3*n-3
k1 = 4*n-5
for k in range(n-2):
T.G[k+k0,:]= [k+2,2*n-2-k]
T.G[k+k1,:]= [k+1,2*n-2-k-1]
return T
#
plt.figure(figsize=(12,6))
plt.subplot(1,2,1)
T1 = treillis1c(3,2.,1.)
T1.trace()
plt.subplot(1,2,2)
T2 = treillis1c(5,2.,1.)
T2.trace()
def treillis2(n,L,H):
"""treillis type 2"""
T = Treillis()
T.nn = 2*n
T.X = np.zeros((T.nn,2),dtype=float)
T.ne = 3*(n-1)+1
T.G = np.zeros((T.ne,2),dtype=int)
for i in range(n):
T.X[i,0] = i*L/(n-1)
T.X[i,1] = 0.
for i in range(n):
T.X[n+i,0] = (n-i-1)*L/(n-1)
T.X[n+i,1] = (n-i)*H/(n)
for k in range(n-1):
T.G[k,:] = [k,k+1]
T.G[k+n-1,:] = [n+k,n+k+1]
T.G[k+2*n-2,:] = [k+1,2*n-2-k]
T.G[-1,:] = [T.nn-1,0]
return T
#
plt.figure(figsize=(12,6))
plt.subplot(1,2,1)
T1 = treillis2(3,2.,1.)
T1.trace()
plt.subplot(1,2,2)
T2 = treillis2(4,2.,1.)
T2.trace()
def treillis2a(n,L,H):
"""treillis type 2 variante 1"""
T = Treillis()
T.nn = 2*n
T.X = np.zeros((T.nn,2),dtype=float)
T.ne = 3*(n-1)+ 1 + (n-1)
T.G = np.zeros((T.ne,2),dtype=int)
for i in range(n):
T.X[i,0] = i*L/(n-1)
T.X[i,1] = 0.
for i in range(n):
T.X[n+i,0] = (n-i-1)*L/(n-1)
T.X[n+i,1] = (n-i)*H/(n)
for k in range(n-1):
T.G[k,:] = [k,k+1]
T.G[k+n-1,:] = [n+k,n+k+1]
T.G[k+2*n-2,:] = [k+1,2*n-2-k]
k0 = 3*n-3
for k in range(n-1):
T.G[k+k0,:]= [k,2*n-2-k]
T.G[-1,:] = [T.nn-1,0]
return T
#
plt.figure(figsize=(12,6))
plt.subplot(1,2,1)
T1 = treillis2a(3,2.,1.)
T1.trace()
plt.subplot(1,2,2)
T2 = treillis2a(4,2.,1.)
T2.trace()
def treillis2b(n,L,H):
"""treillis type 2 variante 2"""
T = Treillis()
T.nn = 2*n
T.X = np.zeros((T.nn,2),dtype=float)
T.ne = 3*(n-1)+ 1 + (n-1)
T.G = np.zeros((T.ne,2),dtype=int)
for i in range(n):
T.X[i,0] = i*L/(n-1)
T.X[i,1] = 0.
for i in range(n):
T.X[n+i,0] = (n-i-1)*L/(n-1)
T.X[n+i,1] = (n-i)*H/(n)
for k in range(n-1):
T.G[k,:] = [k,k+1]
T.G[k+n-1,:] = [n+k,n+k+1]
T.G[k+2*n-2,:] = [k+1,2*n-2-k]
k0 = 3*n-3
for k in range(n-1):
T.G[k+k0,:]= [k+1,2*n-2-k+1]
T.G[-1,:] = [T.nn-1,0]
return T
#
plt.figure(figsize=(12,6))
plt.subplot(1,2,1)
T1 = treillis2b(3,2.,1.)
T1.trace()
plt.subplot(1,2,2)
T2 = treillis2b(4,2.,1.)
T2.trace()
def treillis2c(n,L,H):
"""treillis type 2 variante 3"""
T = Treillis()
T.nn = 2*n
T.X = np.zeros((T.nn,2),dtype=float)
T.ne = 3*(n-1)+ 1 + 2*(n-1)
T.G = np.zeros((T.ne,2),dtype=int)
for i in range(n):
T.X[i,0] = i*L/(n-1)
T.X[i,1] = 0.
for i in range(n):
T.X[n+i,0] = (n-i-1)*L/(n-1)
T.X[n+i,1] = (n-i)*H/(n)
for k in range(n-1):
T.G[k,:] = [k,k+1]
T.G[k+n-1,:] = [n+k,n+k+1]
T.G[k+2*n-2,:] = [k+1,2*n-2-k]
k0 = 3*n-3
k1 = 4*n-4
for k in range(n-1):
T.G[k+k0,:]= [k+1,2*n-2-k+1]
T.G[k+k1,:]= [k,2*n-2-k]
T.G[-1,:] = [T.nn-1,0]
return T
#
plt.figure(figsize=(12,6))
plt.subplot(1,2,1)
T1 = treillis2c(3,2.,1.)
T1.trace()
plt.subplot(1,2,2)
T2 = treillis2c(4,2.,1.)
T2.trace()
1.4.2.3. génération du treillis toit#
def treillis_toit(type_treillis,n,L,H):
"""creation toit treillis"""
T1 = type_treillis(n,L,H)
T2 = T1.symmetrie(L)
# creation nouveau treillis
T = Treillis()
T.nn = 2*T1.nn-2
T.ne = 2*T1.ne-1
T.X = np.zeros((T.nn,2))
T.G = np.zeros((T.ne,2),dtype=int)
# 2 nds communs n1,n2 et une barre
n1 = n-1
n2 = n
k1 = -1
for k in range(T1.ne):
if (T1.G[k,0]== n1) and (T1.G[k,1]== n2): k1=k
# renumerotation des nds de T2
ni = T2.nn
newnum = np.zeros(T2.nn,dtype=int)
for i in range(T2.nn):
newnum[i] = i
T.X[i,:] = T1.X[i,:]
if (i != n1) and (i!=n2) :
newnum[i] = ni
T.X[ni,:] = T2.X[i,:]
ni = ni+1
# et des elts
nk = T2.ne
for k in range(T2.ne):
T.G[k,:] = T1.G[k,:]
if k!=k1 :
T.G[nk,:] = [newnum[T2.G[k,0]],newnum[T2.G[k,1]]]
nk = nk+1
return T
1.4.3. Analyse#
1.4.3.1. parametres géométriques#
longueur L
hauteur H
ecartement des pannes W
# longueur L, ecartement des pannes W
L = 10
W = L/10
H = 3
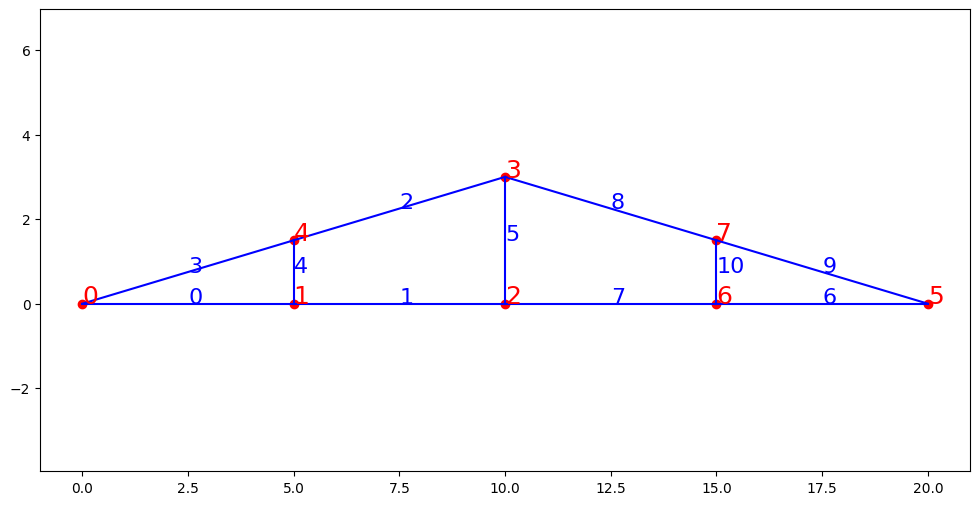
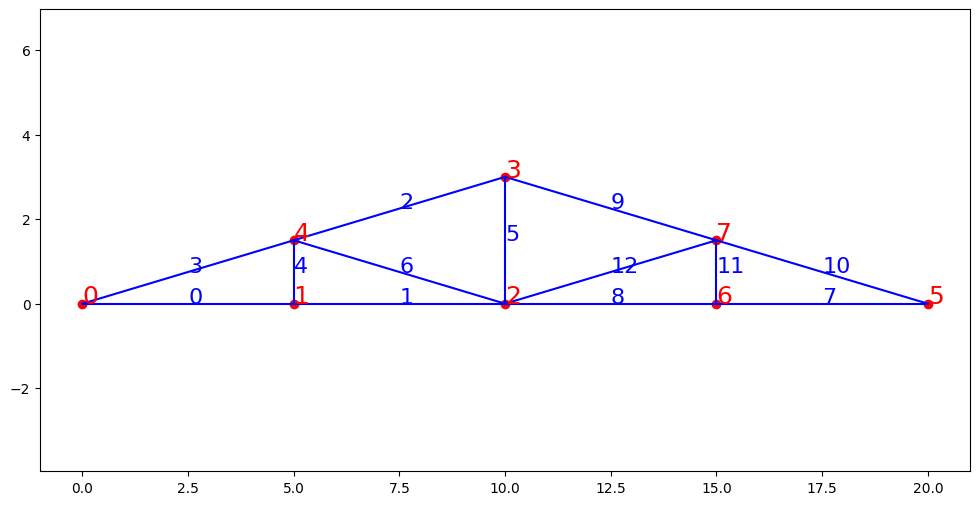
T = treillis_toit(treillis1,3,L,H)
plt.figure(figsize=(12,6))
T.trace()
T.write('treillis_toit1.dat')
1.4.3.2. modele et parametres numériques#
# barre
# poids neige mouillée hauteur 1 m
S = 2*L*W
rho_neige = 300
h = 1.0
# charge / m2
rho_toit = 100
g = 9.81
# cout de vent 80 km/h
U0 = 80*1000/3600
p0 = 0.5*1.0*U0**2
print(rho_neige*h, rho_toit, p0)
# force
Pn = (rho_neige*h + rho_toit + p0)*S*g
# repartition homogene au nds
F = Pn/2
print(F)
300.0 100 246.91358024691357
63462.222222222226
# acier de construction: modyle young et limite elastique sigma_max
E = 210*1.e9
Re = 300*1.e6
rho_acier = 8000
# section des poutres creuses
d = 0.10
e = 0.01
Sd = np.pi*(d-e)*e
sigma = F/Sd
dh = sigma*h/E
print(sigma,sigma/Re,dh)
22445169.70280665 0.07481723234268883 0.00010688176048955548
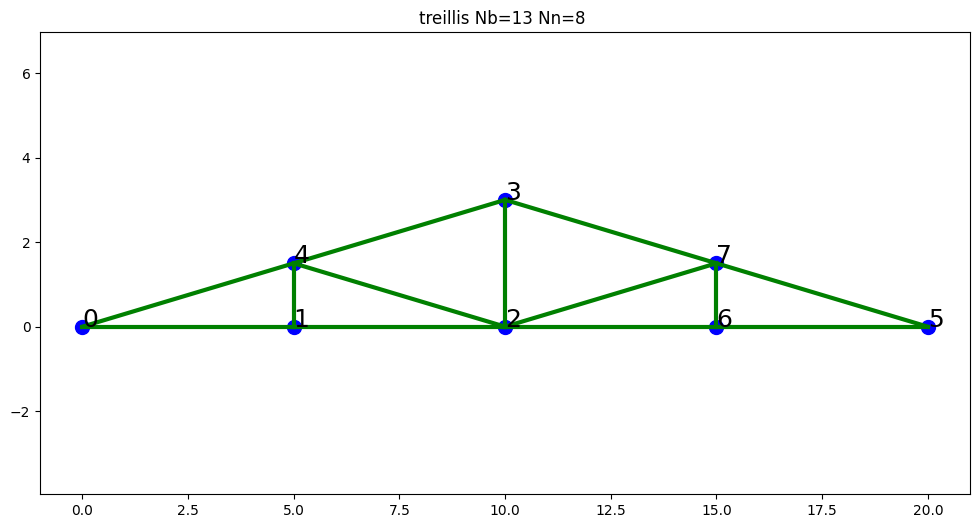
T = treillis_toit(treillis1b,3,L,H)
T.E = E
T.rho = rho_acier
plt.figure(figsize=(12,6))
T.trace()
T.write('treillis_toit.dat')
1.4.3.3. questions#
déformation / limite élastique
allégement du treillis
modes de vibration
# Strouhal St = f*h/U0 ~ 0.2
St = 0.2
f = St*U0*1000/3600*H
print(St," frequence:",f)
0.2 frequence: 3.7037037037037033
# analyse en vibration
import Treillis.treillis as Tr
tr = Tr.Treillis("treillis.dat")
tr.nn = T.nn
tr.ne = T.ne
tr.X = T.X.copy()
tr.G = T.G.copy()
plt.figure(figsize=(12,6))
Tr.trace_treillis(tr,"treillis")
tr.E = 210*1.e9
tr.S = Sd
tr.rho = 8000
# CL
tr.CL = np.zeros(tr.nn,dtype=int)
tr.CL[0]=3
tr.CL[5]=3
# force
tr.FCL = np.zeros((tr.nn,2))
from scipy import linalg
# matrice de masse et de rigidite
BB = np.zeros(2*tr.nn)
KK = Tr.assemblage(tr)
K,B = Tr.climites(tr,KK,BB)
MM = Tr.assemblage_masse(tr)
M,B = Tr.climites(tr,MM,BB)
# valeurs propres
vp,VP=linalg.eig(K,b=M)
vp=np.real(vp)
ip=np.argsort(vp)
print("VP=",vp[np.ix_(ip)],"\nIP=",ip)
nr = 4
print("Nbre de modes rigides ",nr)
fp=np.sqrt(vp[np.ix_(ip)])/(2*np.pi)
fp=fp[nr:]
print("Frequences propres ",fp)
VP= [1.00000000e+00 1.00000000e+00 1.00000000e+00 1.00000000e+00
6.34902595e+04 1.63257593e+05 5.09901759e+05 1.05217984e+06
1.94491099e+06 2.67920529e+06 3.15000000e+06 5.43353882e+06
8.72318069e+06 2.59596924e+07 8.91167834e+07 9.22353573e+07]
IP= [12 13 14 15 9 5 6 10 7 11 4 3 2 8 1 0]
Nbre de modes rigides 4
Frequences propres [ 40.10270641 64.30678925 113.64841591 163.25448458 221.95758791
260.5092376 282.47200236 370.98941498 470.06462137 810.9048586
1502.44949775 1528.51198668]
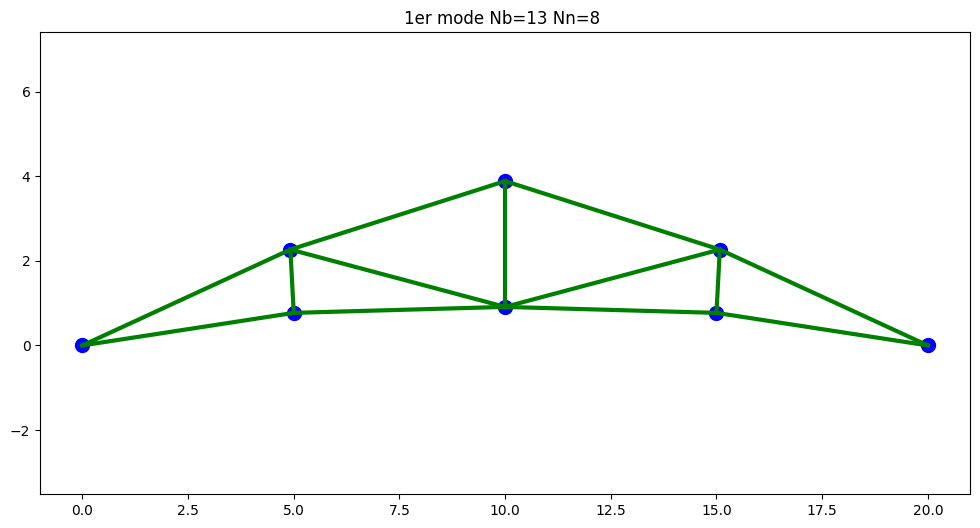
# 1er mode
mode=nr
print("mode ",mode," f=",fp[mode-nr])
U=VP[:,ip[mode]]/linalg.norm(VP[:,ip[mode]])
U=U.reshape((tr.nn,2))
print(U)
# tracer du mode
plt.figure(figsize=(12,6))
Tr.trace_treillis(tr,"1er mode",U*2.,False)
plt.show()
mode 4 f= 40.102706409167546
[[ 0.00000000e+00 0.00000000e+00]
[ 1.78997734e-16 3.85229015e-01]
[ 3.34403435e-16 4.55953501e-01]
[-6.25291864e-16 4.43806672e-01]
[-3.96737865e-02 3.84181752e-01]
[ 0.00000000e+00 0.00000000e+00]
[ 1.28204607e-16 3.85229015e-01]
[ 3.96737865e-02 3.84181752e-01]]