3. TP modélisation de propriétés mécaniques par machine learning#
Marc Buffat, dpt mécanique, UCB Lyon 1
3.1. Objectifs#
L’objectif du TP est la prédiction des propriétés mécaniques des aciers en fonction de la température et de la composition. Pour cela, on va utiliser machine learning à partir d’une base de données expérimentale, en procédant par étape.
On étudie un acier en particulier
ON fait ensuite l’analyse complète pour tous les aciers
3.2. Base de données matériaux#
database : “Propriétés mécaniques des aciers faiblement alliés” disponible sur le site Kaggle (site de partage sur IA et database IA), qui contient la composition de l’alliage, la température et les propriétés mécaniques
Contexte : il n’existe actuellement aucune méthode théorique précise pour prédire les propriétés mécaniques des aciers. Toutes les méthodes disponibles sont étayées par des statistiques et des tests physiques approfondis des matériaux. Puisque tester chaque matériau avec une composition différente est une tâche très fastidieuse (imaginez le nombre de possibilités !), on utilise un apprentissage automatique et des statistiques pour résoudre ce problème.
Contenu : ce jeu de données contient des compositions en pourcentages massiques d’aciers faiblement alliés ainsi que les températures auxquelles les aciers ont été testés et les valeurs de propriétés mécaniques observées lors des tests. Le code d’alliage est une chaîne unique à chaque alliage. Les pourcentages en poids des métaux d’alliage et des impuretés comme l’aluminium, le cuivre, le manganèse, l’azote, le nickel, le cobalt, le carbone, etc. sont indiqués dans des colonnes. La température en Celsius pour chaque essai est mentionnée dans une colonne. Enfin, les propriétés mécaniques, y compris la résistance à la traction, la limite d’élasticité, l’allongement et la réduction de surface sont indiquées dans des colonnes séparées. L’ensemble de données est dans un fichier csv de 915 lignes (mesures).
%matplotlib inline
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from IPython.display import display,Markdown
def printmd(text):
display(Markdown(text))
plt.rc('font', family='serif', size='18')
# bibliothéque IA
import seaborn as sns
import sklearn as sk
3.3. Lecture de la base de données#
fname = '/home/cours/DatabaseIA/data_mechanical-properties/mechanical_properties_of_low-alloy_steels.csv'
dataset = pd.read_csv(fname)
# simplification et nettoyage du nom des colonnes (enlève les espaces)
new_list = {'Alloy code' : 'code',
' C': 'C',
' Si': 'Si',
' Mn': 'Mn',
' P' : 'P',
' S' : 'S',
' Ni': 'Ni',
' Cr': 'Cr',
' Mo': 'Mo',
' Cu': 'Cu',
' Al': 'Al',
' N' : 'N',
'Nb + Ta': 'Nb+Ta',
' Temperature (°C)': 'temperature',
' 0.2% Proof Stress (MPa)': 'elasticite',
' Tensile Strength (MPa)': 'rupture',
' Elongation (%)': 'elongation',
' Reduction in Area (%)': 'striction'}
dataset.rename(columns=new_list, inplace=True)
dataset.info()
# liste des alliages
CODE = dataset['code'].value_counts().sort_index()
display("Code des Alliages:",CODE)
---------------------------------------------------------------------------
FileNotFoundError Traceback (most recent call last)
Cell In[2], line 2
1 fname = '/home/cours/DatabaseIA/data_mechanical-properties/mechanical_properties_of_low-alloy_steels.csv'
----> 2 dataset = pd.read_csv(fname)
3 # simplification et nettoyage du nom des colonnes (enlève les espaces)
4 new_list = {'Alloy code' : 'code',
5 ' C': 'C',
6 ' Si': 'Si',
(...)
20 ' Elongation (%)': 'elongation',
21 ' Reduction in Area (%)': 'striction'}
File ~/venvs/jupyter/lib/python3.10/site-packages/pandas/util/_decorators.py:211, in deprecate_kwarg.<locals>._deprecate_kwarg.<locals>.wrapper(*args, **kwargs)
209 else:
210 kwargs[new_arg_name] = new_arg_value
--> 211 return func(*args, **kwargs)
File ~/venvs/jupyter/lib/python3.10/site-packages/pandas/util/_decorators.py:331, in deprecate_nonkeyword_arguments.<locals>.decorate.<locals>.wrapper(*args, **kwargs)
325 if len(args) > num_allow_args:
326 warnings.warn(
327 msg.format(arguments=_format_argument_list(allow_args)),
328 FutureWarning,
329 stacklevel=find_stack_level(),
330 )
--> 331 return func(*args, **kwargs)
File ~/venvs/jupyter/lib/python3.10/site-packages/pandas/io/parsers/readers.py:950, in read_csv(filepath_or_buffer, sep, delimiter, header, names, index_col, usecols, squeeze, prefix, mangle_dupe_cols, dtype, engine, converters, true_values, false_values, skipinitialspace, skiprows, skipfooter, nrows, na_values, keep_default_na, na_filter, verbose, skip_blank_lines, parse_dates, infer_datetime_format, keep_date_col, date_parser, dayfirst, cache_dates, iterator, chunksize, compression, thousands, decimal, lineterminator, quotechar, quoting, doublequote, escapechar, comment, encoding, encoding_errors, dialect, error_bad_lines, warn_bad_lines, on_bad_lines, delim_whitespace, low_memory, memory_map, float_precision, storage_options)
935 kwds_defaults = _refine_defaults_read(
936 dialect,
937 delimiter,
(...)
946 defaults={"delimiter": ","},
947 )
948 kwds.update(kwds_defaults)
--> 950 return _read(filepath_or_buffer, kwds)
File ~/venvs/jupyter/lib/python3.10/site-packages/pandas/io/parsers/readers.py:605, in _read(filepath_or_buffer, kwds)
602 _validate_names(kwds.get("names", None))
604 # Create the parser.
--> 605 parser = TextFileReader(filepath_or_buffer, **kwds)
607 if chunksize or iterator:
608 return parser
File ~/venvs/jupyter/lib/python3.10/site-packages/pandas/io/parsers/readers.py:1442, in TextFileReader.__init__(self, f, engine, **kwds)
1439 self.options["has_index_names"] = kwds["has_index_names"]
1441 self.handles: IOHandles | None = None
-> 1442 self._engine = self._make_engine(f, self.engine)
File ~/venvs/jupyter/lib/python3.10/site-packages/pandas/io/parsers/readers.py:1735, in TextFileReader._make_engine(self, f, engine)
1733 if "b" not in mode:
1734 mode += "b"
-> 1735 self.handles = get_handle(
1736 f,
1737 mode,
1738 encoding=self.options.get("encoding", None),
1739 compression=self.options.get("compression", None),
1740 memory_map=self.options.get("memory_map", False),
1741 is_text=is_text,
1742 errors=self.options.get("encoding_errors", "strict"),
1743 storage_options=self.options.get("storage_options", None),
1744 )
1745 assert self.handles is not None
1746 f = self.handles.handle
File ~/venvs/jupyter/lib/python3.10/site-packages/pandas/io/common.py:856, in get_handle(path_or_buf, mode, encoding, compression, memory_map, is_text, errors, storage_options)
851 elif isinstance(handle, str):
852 # Check whether the filename is to be opened in binary mode.
853 # Binary mode does not support 'encoding' and 'newline'.
854 if ioargs.encoding and "b" not in ioargs.mode:
855 # Encoding
--> 856 handle = open(
857 handle,
858 ioargs.mode,
859 encoding=ioargs.encoding,
860 errors=errors,
861 newline="",
862 )
863 else:
864 # Binary mode
865 handle = open(handle, ioargs.mode)
FileNotFoundError: [Errno 2] No such file or directory: '/home/cours/DatabaseIA/data_mechanical-properties/mechanical_properties_of_low-alloy_steels.csv'
from validation.valide_markdown import test_markdown
from validation.validation import info_etudiant
try: NUMERO_ETUDIANT
except NameError: NUMERO_ETUDIANT = None
if type(NUMERO_ETUDIANT) is not int :
printmd("**ERREUR:** numéro d'étudiant non spécifié!!!")
NOM,PRENOM,NUMERO_ETUDIANT=info_etudiant()
#raise AssertionError("NUMERO_ETUDIANT non défini")
# parametres spécifiques
_uid_ = NUMERO_ETUDIANT
np.random.seed(_uid_)
code=np.random.randint(95)
acier = CODE.index[code]
printmd("**Login étudiant {} {} uid={} ({})**".format(NOM,PRENOM,_uid_,code))
printmd(f"** Code de l'acier a étudier: {acier}**")
3.4. Etude d’un acier particulier#
choix d’un acier dans la base de données: nom dans la variable acier
extraire les donnees de cet acier dans la base de données et les mettre dans data_acier
nettoyer la base de données en en enlevant les colonnes non nécessaires (composition, nom=
data_acier = None
### BEGIN SOLUTION
printmd("### acier étudié "+acier)
data_acier = dataset.loc[(dataset['code']==acier)].copy()
# nettoyage de la base en enlevent les colonnes
data_acier.drop(data_acier.columns[np.arange(15)],axis=1,inplace=True)
data_acier.info()
### END SOLUTION
printmd("### base de données pour l'acier étudié "+acier)
assert (data_acier.shape[1] == 5)
3.4.1. Analyse des données#
L’objectif est la prédiction des propriétés mécaniques des aciers en fonction de la température et de la composition. La composition de l’acier étant fixé ici, les données sont donc uniquement la température, pour prédire les propriétés mécaniques.
3.4.1.1. visualisation des données#
visualisation des données
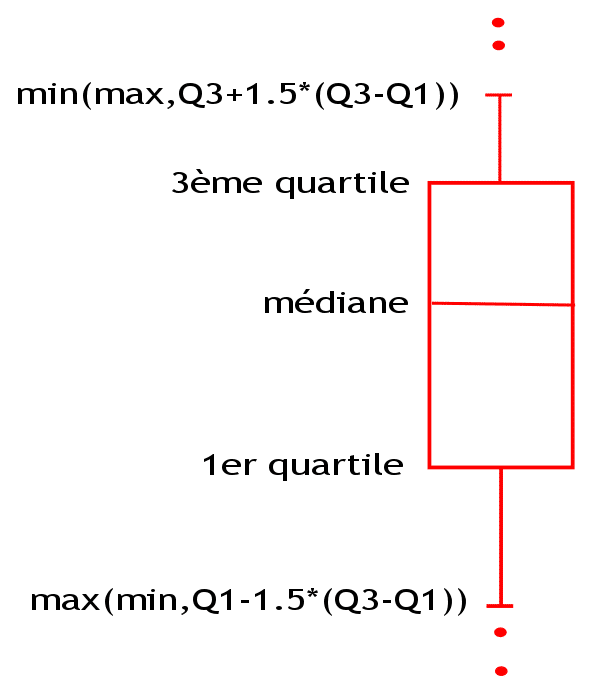
visualisation des données statistiques (boite à moustache ou boxplot)
matrice corrélations
# visualisation
plt.figure(figsize=(14,6))
ax1 = plt.subplot(1,2,1)
data_acier.plot.scatter(x='temperature',y='elongation',s=50,title=f"acier {acier}",label="allongement",ax=ax1)
data_acier.plot.scatter(x='temperature',y='striction',s=50,label=f"striction",ax=ax1,color='r')
ax1.set_ylabel("en %")
ax2 = plt.subplot(1,2,2)
data_acier.plot.scatter(x='temperature',y='elasticite',s=50,title=f"acier {acier}",label="élastique",ax=ax2)
data_acier.plot.scatter(x='temperature',y='rupture',s=50,label="rupture",ax=ax2,color='r')
ax2.set_ylabel("limite en MPa");
# bilan statistique
plt.figure(figsize=(14,6))
ax1 = plt.subplot(1,2,1)
data_acier.boxplot(column=["elongation","striction"],showmeans=True,ax=ax1)
ax1 = plt.subplot(1,2,2)
data_acier.boxplot(column=["elasticite","rupture"],showmeans=True,ax=ax1);
# correlations
corr = data_acier.corr()
plt.subplots(figsize=(16,12))
sns.heatmap(corr, xticklabels=corr.columns, yticklabels=corr.columns, annot=True)
3.4.1.2. analyse statistique#
\(\bar{y}\) moyenne /médiane
\(\sigma\) écart type : dispersion autour de la moyenne (pour une gaussienne, 68% entre \(\bar{y}-\sigma\) et \(\bar{y}+\sigma\) )
\(\eta\) skewness : (coefficient d’asymétrie) correspond à une mesure de l’asymétrie de la distribution
\(\eta=0\) indique une distribution symétrique.
\(\eta<0\) indique une distribution décalée à droite de la médiane, et donc une queue de distribution étalée vers la gauche.
\(\eta>0\) indique une distribution décalée à gauche de la médiane, et donc une queue de distribution étalée vers la droite.
\(C_{1,2}\) corrélation entre 2 variables \(y_1\) et \(y_2\)
- signe >0: niveau de dépendence linéaire directe (croissance)
- signe <0: niveau de dépendence linéaire indirecte (décroissance)
Corrélation |
Négative |
Positive |
|---|---|---|
Faible |
de −0,5 à 0,0 |
de 0,0 à 0,5 |
Forte |
de −1,0 à −0,5 |
de 0,5 à 1,0 |
En utilisant pandas, calculer les données statistiques (describe) et en particulier le skewness pour les 4 propriétés mécaniques, que l’on mettra dans les variables indiquées
elongation dans skew1
striction dans skew2
limite elastique dans skew3
limite rupture dans skew4
# données statitiques
skew1 = None
skew2 = None
skew3 = None
skew4 = None
### BEGIN SOLUTION
printmd(f"## Acier {acier}")
data_acier.describe()
# niveau de disymétrie
skew1 = data_acier["elongation"].skew()
skew2 = data_acier["striction"].skew()
skew3 = data_acier["elasticite"].skew()
skew4 = data_acier["rupture"].skew()
### END SOLUTION
printmd(f"## skewness: elongation={skew1:.2f} striction={skew2:.2f} limite elasticité={skew3:.2f} rupture={skew4:.2f}")
assert( np.allclose(pd.DataFrame.skew(data_acier)[1:5],[skew3,skew4,skew1,skew2]))
3.5. Données pour le machine learning#
Création des données pour l’apprentissage automatique: données X et prédiction y
X input features = temperature
y data to predict
elongation
striction
limite elastique
limite rupture
X = None
y = None
### BEGIN SOLUTION
X = data_acier.iloc[:, :1].values
y = data_acier.iloc[:,1:].values
### END SOLUTION
print("data : ",X.shape,y.shape)
assert( (X.shape[1]==1) and (y.shape[1]==4))
3.5.1. Mise à l’échelle#
pour une analyse plus précise on fait un scaling des données mécaniques:
en utilisant par exemple:
scikit learn preprocess StandardScaler
on met le résultat dans la variable
ys
pour la température, on choisit un scaling différent du type:
from sklearn.preprocessing import StandardScaler
Xs = None
ys = None
### BEGIN SOLUTION
Xs = (X - X.min())/(X.max()-X.min())
scaler = StandardScaler()
scaley = scaler.fit(y)
ys = scaley.transform(y,copy=True)
### END SOLUTION
print(Xs.min(),Xs.max(),ys[:,0].min(),ys[:,0].max())
assert(np.abs(Xs.min()) < 1.e-5)
assert(np.abs(ys[:,0].min()-(y[:,0].min()-y[:,0].mean())/np.sqrt(y[:,0].var())) < 1.e-5)
3.5.2. Outils#
fonction de tracer pour comparer les prédictions avec les mesures
def traceXY(X,y, Xpred,ypred):
"""tracer les mesures y=f(X) et la prédiction ypred=f(Xpred)"""
plt.figure(figsize=(12,6))
plt.subplot(1,2,1)
plt.scatter(X[:,0],y[:,0],c='b')
plt.plot(Xpred[:,0],ypred[:,0],'--r',label='elast.')
plt.scatter(X[:,0],y[:,1],c='g')
plt.plot(Xpred[:,0],ypred[:,1],'--c',label='rupt.')
plt.legend()
plt.xlabel('T en °C')
plt.ylabel('lim. en Mpa')
plt.title(f"limite {acier}");
plt.subplot(1,2,2)
plt.scatter(X[:,0],y[:,2],c='b')
plt.plot(Xpred[:,0],ypred[:,2],'--r',label='allong.')
plt.scatter(X[:,0],y[:,3],c='g')
plt.plot(Xpred[:,0],ypred[:,3],'--c',label='stric.')
plt.legend()
plt.xlabel('T en °C')
plt.title(f"en % {acier}")
return
def traceYY(y,ypred):
"""tracer la prédiction en fct des mesures: ideal=droite"""
plt.figure(figsize=(12,6))
plt.subplot(1,2,1)
plt.scatter(y[:,2],ypred[:,2])
x1 = np.linspace(np.min(y[:,2]),np.max(y[:,2]),51)
plt.plot(x1,x1,'--r',lw=2)
plt.title("allongement")
plt.xlabel("mesures")
plt.ylabel("predict.")
plt.axis('equal')
plt.subplot(1,2,2)
plt.scatter(y[:,3],ypred[:,3])
x1 = np.linspace(np.min(y[:,3]),np.max(y[:,3]),51)
plt.plot(x1,x1,'--r',lw=2)
plt.title("striction")
plt.xlabel("mesures")
plt.axis('equal');
return
def plotY(y_test,ypred,titre=""):
plt.figure(figsize=(8,6))
plt.scatter(y_test[:],ypred[:])
x1 = np.linspace(np.min(y_test[:]),np.max(y_test[:]),51)
plt.plot(x1,x1,'--r',lw=2)
plt.title(f"pred. allongement par {titre}")
plt.xlabel("mesures")
plt.ylabel("predictions")
plt.axis('equal');
return
3.6. Algorithme de machine learning#
3.6.1. Linear regression#
calculer la prédiction ypred et le R2 score dans ypred et r2
comparer les mesures avec la prédiction en utilisant traceYY
# training the multiple Linear regression model on the training set
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
ypred = None
r2 = None
### BEGIN SOLUTION
reg = LinearRegression()
reg = reg.fit(Xs, ys)
print("Score = {:2d}%".format(int(100*reg.score(Xs, ys))))
ypred = reg.predict(Xs)
r2 = r2_score(ys, ypred)
print("R2 score {:.2f}".format(r2))
traceYY(ys,ypred)
### END SOLUTION
assert(ypred.shape == ys.shape)
assert(r2 != 0)
3.6.2. prédictions linear regression#
Calculer la prédiction pour une gamme de température de 50 a 550 °C
résultats dans Xpred et ypred (valeur dimensionnelle)
tracer le résultat avec traceXY (sous forme dimensionnelle)
# prediction
Xpred = None
ypred = None
### BEGIN SOLUTION
Xpred = np.linspace(50,550,101).reshape((101,1))
# prediction sans dimension
Xp = (Xpred-X.min())/(X.max()-X.min())
yp = reg.predict(Xp)
#
ypred = scaley.inverse_transform(yp)
traceXY(X,y,Xpred,ypred)
### END SOLUTION
assert((Xpred.shape[0] == ypred.shape[0]) and (ypred.shape[1] == 4))
3.6.3. Random forest#
calculer la prédiction ypred et le R2 score dans ypred et r2
comparer les mesures avec la prédiction en utilisant traceYY
from sklearn.ensemble import RandomForestRegressor
ypred = None
r2 = None
### BEGIN SOLUTION
clf = RandomForestRegressor(n_estimators=100, criterion='squared_error')
clf = clf.fit(Xs,ys)
print("Score = {:2d}%".format(int(100*clf.score(Xs, ys))))
ypred = clf.predict(Xs)
r2 = r2_score(ys, ypred)
print("R2 score {:.2f}".format(r2))
traceYY(ys,ypred)
### END SOLUTION
assert(ypred.shape == y.shape)
assert(r2 != 0)
3.6.4. prédictions random forest#
Calculer la prédiction pour une gamme de température de 50 a 550 °C
résultats dans Xpred et ypred
tracer le résultat avec traceXY
# prediction
Xpred = None
ypred = None
### BEGIN SOLUTION
Xpred = np.linspace(50,550,101).reshape((101,1))
Xp = (Xpred-X.min())/(X.max()-X.min())
yp = clf.predict(Xp)
#
ypred = scaley.inverse_transform(yp)
traceXY(X,y,Xpred,ypred)
### END SOLUTION
assert((Xpred.shape[0] == ypred.shape[0]) and (ypred.shape[1] == 4))
3.6.5. K plus proches voisins KNN#
calculer la prédiction ypred et le R2 score dans ypred et r2
comparer les mesures avec la prédiction en utilisant traceYY
from sklearn.neighbors import KNeighborsRegressor
ypred = None
r2 = None
### BEGIN SOLUTION
neigh = KNeighborsRegressor(n_neighbors=5)
neigh = neigh.fit(Xs, ys)
print("score = {:2d}%".format(int(100*neigh.score(Xs, ys))))
ypred = neigh.predict(Xs)
r2 = r2_score(ys, ypred)
print("R2 score {:.2f}".format(r2))
traceYY(ys,ypred)
### END SOLUTION
assert(ypred.shape == y.shape)
assert(r2 != 0)
3.6.6. prédictions KNN#
Calculer la prédiction pour une gamme de température de 50 a 550 °C
résultats dans Xpred et ypred
tracer le résultat avec traceXY
# prediction
Xpred = None
ypred = None
### BEGIN SOLUTION
Xpred = np.linspace(50,550,101).reshape((101,1))
Xp = (Xpred-X.min())/(X.max()-X.min())
yp = neigh.predict(Xp)
#
ypred = scaley.inverse_transform(yp)
traceXY(X,y,Xpred,ypred)
### END SOLUTION
assert((Xpred.shape[0] == ypred.shape[0]) and (ypred.shape[1] == 4))
3.7. Analyse globale avec la composition et la température#
objectif: prédiction de l’allongement en fonction de la température et de la composition des aciers
à partir de la base de données initiale, définir les données X et la prédiction y (allongement uniquement)
séparer ensuite la base de données en 2 parties:
une base de données d’entraînement: X_train, y_train (80% des données)
une base de données de test: X_test, y_test (20 % des données)
on utilisera pour cela la fonction train_test_split avec comme paramètres
train_size = 0.8, shuffle = True, random_state = NUMERO_ETUDIANT
from sklearn.model_selection import train_test_split
X = None
y = None
X_train = None
y_train = None
X_test = None
y_test = None
### BEGIN SOLUTION
X = dataset.iloc[:,1:16].values
y = dataset.iloc[:,18:19].values
# Making the train test split
X_train, X_test, y_train, y_test = train_test_split(X, y[:,0], train_size = 0.8, shuffle = True,
random_state = NUMERO_ETUDIANT)
### END SOLUTION
print("data : ",X.shape,y.shape,X_train.shape,X_test.shape,y_test.shape)
assert(X.shape[0] == X_train.shape[0] + X_test.shape[0])
assert([X.shape[1],X_train.shape[1],X_test.shape[1]] == [15,15,15])
assert(len(y) == len(y_train)+len(y_test))
3.7.1. Réseaux de neurones#
utilisation de la base de données d’entraînement X_train, y_train
apprentissage avec X_train, y_train
calculer la prédiction ypred et le R2 score dans ypred et r2 avec la base de test
tracer la prediction versus les mesures avec plotY
from sklearn.neural_network import MLPRegressor
ypred = None
r2 = None
### BEGIN SOLUTION
clf = MLPRegressor( max_iter=800, random_state=0, activation='relu', solver="adam", verbose =False)
clf = clf.fit(X_train,y_train)
print("score = {:2d}%".format(int(100*clf.score(X_train, y_train))))
ypred = clf.predict(X_test)
r2 = r2_score(y_test, ypred)
print("R2 score {:.2f}".format(r2))
plotY(y_test,ypred,"réseaux de neuronnes")
### END SOLUTION
assert(ypred.shape == y_test.shape)
assert(r2 != 0)
3.7.2. Random forest#
utilisation de la base de données d’entraînement X_train, y_train
apprentissage avec X_train, y_train
calculer la prédiction ypred et le R2 score dans ypred et r2 avec la base de test
tracer la prediction versus les mesures avec plotY
ypred = None
r2 = None
### BEGIN SOLUTION
clf = RandomForestRegressor(n_estimators=100, criterion='squared_error')
clf = clf.fit(X_train,y_train)
print("Score = {:2d}%".format(int(100*clf.score(X_train, y_train))))
ypred = clf.predict(X_test)
r2 = r2_score(y_test, ypred)
print("R2 score {:.2f}".format(r2))
plotY(y_test,ypred,"Random Forest")
### END SOLUTION
assert(ypred.shape == y_test.shape)
assert(r2 != 0)
3.8. Etude avec mise a l’échelle#
Refaire l’étude en utilisant des données mise à l’échelle
à partir de la base de données initiale, définir les données Xs et la prédiction ys (allongement uniquement) avec une mise a l’échelle
séparer ensuite la base de données en 2 parties:
une base de données d’entraînement: X_train, y_train (80% des données)
une base de données de test: X_test, y_test (20 % des données)
on utilisera pour cela la fonction train_test_split avec comme paramètres
train_size = 0.8, shuffle = True, random_state = NUMERO_ETUDIANT
print("taille de la BD:",X.shape, y.shape)
Xs = None
Ys = None
X_train = None
y_train = None
X_test = None
y_test = None
### BEGIN SOLUTION
scaler = StandardScaler()
n = X.shape[0]
p = X.shape[1]
Xs = np.zeros((n,p))
for i in range(p):
xx = X[:,i].reshape(n,1)
scaleX = scaler.fit(xx)
Xs[:,i] = scaleX.transform(xx)[:,0]
scaley = scaler.fit(y)
ys = scaley.transform(y)
# Making the train test split
X_train, X_test, y_train, y_test = train_test_split(Xs, ys[:,0], train_size = 0.8, shuffle = True,
random_state = NUMERO_ETUDIANT)
### END SOLUTION
print("data : ",Xs.shape,ys.shape,X_train.shape,X_test.shape,y_train.shape)
assert(Xs.shape[0] == X_train.shape[0] + X_test.shape[0])
assert([Xs.shape[1],X_train.shape[1],X_test.shape[1]] == [15,15,15])
assert(len(ys) == len(y_train)+len(y_test))
3.8.1. Réseaux de neurones#
utilisation de la base de données d’entraînement X_train, y_train
apprentissage avec X_train, y_train
calculer la prédiction ypred et le R2 score dans ypred et r2 avec la base de test
tracer la prediction versus les mesures avec plotY
le paramètre hidden_layer_sizes est un tupple dont la taille représente le nombre de couches et chaque élément représente le nombre de neurones / couche
si on veut un modèle avec 3 couches de 100 Neurones chacune, on doit mettre :
hidden_layer_sizes = (100,100,100).
Donc la valeur par défaut représente bien une seule couche cachée de 100 Neurones.
ypred = None
r2 = None
### BEGIN SOLUTION
clf = MLPRegressor( max_iter=800, random_state=0, activation='relu', solver="adam", verbose =False)
clf = clf.fit(X_train,y_train)
print("score = {:2d}%".format(int(100*clf.score(X_train, y_train))))
ypred = clf.predict(X_test)
r2 = r2_score(y_test, ypred)
print("R2 score {:.2f}".format(r2))
plotY(y_test,ypred,"réseau de neuronnes")
### END SOLUTION
assert(ypred.shape == y_test.shape)
assert(r2 != 0)
3.8.2. Random Forest#
utilisation de la base de données d’entraînement X_train, y_train
apprentissage avec X_train, y_train
calculer la prédiction ypred et le R2 score dans ypred et r2 avec la base de test
tracer la prediction versus les mesures avec plotY
ypred = None
r2 = None
### BEGIN SOLUTION
clf = RandomForestRegressor(n_estimators=100, criterion='squared_error')
clf = clf.fit(X_train,y_train)
print("Score = {:2d}%".format(int(100*clf.score(X_train, y_train))))
ypred = clf.predict(X_test)
r2 = r2_score(y_test, ypred)
print("R2 score {:.2f}".format(r2))
plotY(y_test,ypred,"random forest")
### END SOLUTION
assert(ypred.shape == y_test.shape)
assert(r2 != 0)
3.9. Conclusion#
dans la cellule suivante écrire votre analyse en markdown
Ecrire en markdown votre analyse et vos conclusions
L’algorithme random forest fonctionne globalement mieux par rapport aux réseaux de neurones. Étant donné qu’il est peu coûteux à entraîner, plus facile à ajuster manuellement et très polyvalent pour s’adapter à des données complexes contenant des régressions au sein de clusters, ce modèle constitue un choix idéal pour la prédiction des propriétés mécaniques des aciers faiblement alliés avec un score qui est significativement supérieur au score du réseau neuronal.
A faire: tester avec le réseau de neuronnes de keras (tensor flow)
# test commentaire
test_markdown('TP2_ptes_mecaniques_IA.ipynb','cell-comment1',40,0.1)
print("Commentaire OK")
