- ... Buffat0.1
- avec l'aide précieuse de Bernard Gay et Hamda BenHadid
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...2.1
- en 1D avec
![$\Omega=[0,1]$](img243.png) , la solution est un polynôme de degré 1
qui dépend de 2 constantes: la condition imposée en
, la solution est un polynôme de degré 1
qui dépend de 2 constantes: la condition imposée en 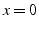 et celle
en
et celle
en 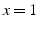 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... conditions2.2
- en 1D avec
![$\Omega=[0,1]$](img243.png) , la solution est un polynôme d'ordre 3,
qui dépend de 4 constantes: les 2 conditions imposées en
, la solution est un polynôme d'ordre 3,
qui dépend de 4 constantes: les 2 conditions imposées en 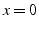 et
les 2 conditions en
et
les 2 conditions en 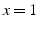 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...2.1
- si
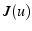 est minimum, alors
est minimum, alors 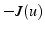 est maximum, et vice et versa
est maximum, et vice et versa
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... continu2.2
- Pour un système discret à
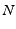 degrés de liberté, la fonction inconnue
degrés de liberté, la fonction inconnue
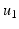 est un vecteur à N composantes
est un vecteur à N composantes
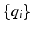 ,
et on obtiens alors les
,
et on obtiens alors les 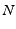 équations de Lagrange:
équations de Lagrange:
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... externes2.3
- conditions aux limites de Neuman (force imposée)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...2.4
- puisque
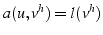 et
et
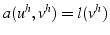
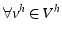 ,
et
,
et 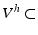 V
V
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...2.5
- les variations
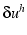 sont des combinaisons linéaires des
fonctions de base
sont des combinaisons linéaires des
fonctions de base
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... approximation2.6
- au sens de la norme
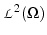 (3.25)
(3.25)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...5.1
- Hydrodynamics by Sir Horace LAMB, Dover Publications N.Y.,
1953
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...FREEFEM5.2
- logiciel écrit par O. Pironneau et C. Prud'Homme disponible sur le
cite
http://www.ann.jussieu.fr/freefem/doc/html/freefem.html
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... approchées5.3
- dans les livres sur les éléments finis, on ne donne en générale que
ces valeurs numériques!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...6.1
- au repos la tension dans la corde est constante
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... positive6.2
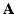 est définie positive si
est définie positive si
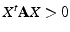 pour
pour 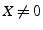
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.