2.1 Une première approche en statique

On considère une poutre encastrée à une extrémité et soumise à une force de traction $F$ dans la direction $x$ (figure 3.3 ).

Figure 3.1: poutre en traction

Comme il a été vue dans le chapitre précédent, l'équation d'équilibre locale des forces en statique s'écrit ( en notant $u_{1}(x)$le déplacement d'une section d'abscisse $x$ , $S$ la section et $E$ le module d'Young):

$$\frac{\partial}{\partial x}\left(ES\frac{\partial u_{1}}{\partial x}\right)=0$$ (2.1)

A cette équation, il faut ajouter 2 conditions aux limites:

1. la condition d'encastrement en $x=0$ (condition de Dirichlet):
   

   $$u_{1}(0) = 0$$ (2.2)

   
   

2. la condition de force imposée en $x=l$ (condition de Neuman):
   
   

   $$ES\left(\frac{\partial u_{1}}{\partial x}\right)_{x=l}=F$$ (2.3)

   
   

Cette formulation du problème correspond à la formulation classique d'équilibre local, qui traduit le principe fondamental de la mécanique $\overrightarrow{F}=m\overrightarrow{\gamma}$. En utilisant le principe des travaux virtuels, on peut écrire une formulation intégrale équivalente. Pour cela on considère un déplacement “virtuel” licite $\delta u_{1}$autour de la position d'équilibre, et on calcul le travail des forces associées à ce déplacement. On multiplie donc l'équation (3.1) par $\delta u_{1}$ et on intègre dans le domaine pour calculer la somme des travaux dans le solide:

$$\int_{0}^{l}\frac{\partial}{\partial x}\left(ES\frac{\partial u_{1}}{\partial x}\right)\delta u_{1}dx=0$$

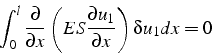
En intégrant par partie, il vient:

$$\int_{0}^{l}ES\frac{\partial u_{1}}{\partial x}\frac{\partia... ...[ES\frac{\partial u_{1}}{\partial x}\delta u_{1}\right]_{0}^{l}$$

On calcule ensuite le terme de bord en utilisant les conditions aux limites. La condition de Neuman (3.3) permet de calculer ce terme en $x=l$. Pour le terme en $x=0$ , on note que le déplacement $\delta u_{1}$est un déplacement licite, qui doit respecter les liaisons. La condition de Dirichlet fixe la valeur de $u_{1}$ en $x=0$, et donc le déplacement $\delta u_{1}$doit s'annuler en $x=0$: $\delta u_{1}(0)=0$. On obtiens ainsi:

$$\underbrace{\int_{0}^{l}ES\frac{\partial u_{1}}{\partial x}\... ...e{F\delta u_{1}(l)}_{\mbox{travail des forces externes}}$$ (2.4)

Cette équation traduit le principe des travaux virtuels appliquée au solide: la somme du travail des forces internes ($contraintes$$\sigma_{xx}$) est égale à la somme du travail fourni par les forces externes (force de traction $F$) pour tous les déplacements virtuels licites vérifiant les liaisons $\delta u_{1}(0)=0$.

C'est la formulation faible de l'équation (3.1) associée aux conditions aux limites (3.2,3.3), qui s'écrit:

$$\left\{ \begin{array}{l} \mbox{Trouvez }u_{1}(x) \mbox{ ... ...ta u_{1} \mbox{ t.q. }\delta u_{1}(0)=0\end{array}\right.$$ (2.5)

En utilisant le calcul des variations, on peut donner une interprétation de l'équation (3.4). En effet cette équation s'écrit sous la forme suivante:

$$\delta\left(\frac{1}{2}\int_{0}^{l}ES\left(\frac{\partial u_{1}}{\partial x}\right)^{2}dx\right)=\delta\left(Fu_{1}(l)\right)$$

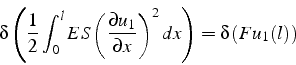
Cette équation traduit la condition de stationnarité ou d'extremum de la quantité $J(u_{1})$

$$J(u_{1})=\underbrace{\frac{1}{2}\int_{0}^{l}ES\left(\frac{\p... ..._{1}}{\partial x}\right)^{2}dx}_{U}-\underbrace{Fu_{1}(l)}_{W}$$ (2.6)

Cette quantité $J(u_{1})$ représente la somme de l'énergie élastique $U$ du solide et du travail “virtuel” $W$ des forces extérieures appliquées. Pour ce problème statique, on peut calculer l'énergie élastique $U$ à l'équilibre en utilisant la formulation faible (3.5). En effet, le déplacement $u_{1}$ et sa variation $\delta u_{1}$vérifient les mêmes conditions aux limites, donc parmi toutes les variations virtuelles licites $\delta u_{1}$, on peut choisir $\delta u_{1}=u_{1}$ dans (3.5). On obtiens ainsi:

$$\int_{0}^{l}ES\left(\frac{\partial u_{1}}{\partial x}\right)^{2}dx=Fu_{1}(l)$$

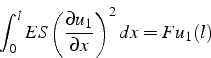
d'où l'expression du potentiel à l'équilibre:

$$U=\frac{1}{2}\int_{0}^{l}ES\left(\frac{\partial u_{1}}{\partial x}\right)^{2}dx=\frac{1}{2}Fu_{1}(l)=\frac{1}{2}W$$

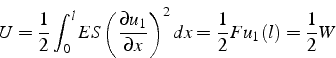
L'énergie élastique à l'équilibre est donc égale à la moitié du travail de la force $F$ pour un déplacement $u_{1}(l)$. C'est l'énergie fournie au solide, lorsque que l'on passe de l'état naturel (i.e. sans contraintes) avec $F=0$ à l'état contraint par la force $F$. Ce passage doit se faire par une succession d'états d'équilibre correspondant à des petites augmentations $\delta F$ de la force pour passer de $0$ à $F$. Dans ce cas le travail fournit est égale à la valeur moyenne $\frac{F}{2}$ de la force (entre 0 et $F)$multipliée par le déplacement $u(l).$ Ce travail fourni est emmagasinée dans le solide sous forme de potentiel élastique. C'est ce que traduit la relation précédente.

On note que la formulation faible ne donne pas le travail réel des forces, mais uniquement un travail virtuel autour de la position d'équilibre pour une variation virtuelle licite autour de cette position. En effet l'équilibre des forces implique l'égalité des travaux de ces forces pour un petit déplacement autour de la position d'équilibre.

A partir de ces relations, on peut en déduire la valeur de la fonctionnelle $J(u_{1})$ à l'équilibre, qui est égale à l'opposé de l'énergie élastique:

$$J(u_{1})=U-W=-U$$

La condition de stationnarité de $J(u_{1})$, qui dans ce cas est un minimum, correspond à la formulation variationnelle de l'équation (3.1) associée aux conditions aux limites (3.2,3.3), et s'écrit:

$$\left\{ \begin{array}{l} \mbox{Trouvez }u_{1}(x) \mbox{ ... ...c{\partial u}{\partial x}\right)^{2}dx-Fu(l)\end{array}\right.$$ (2.7)

Pour un même problème, on a donc 3 formulations équivalentes:

1. la formulation locale des équations d'équilibre:
   c'est une équation aux dérivées partielles (3.1) associée à des conditions aux limites (3.2,3.3).
2. la formulation faible ou principe des travaux virtuels:
   c'est une formulation intégrale (3.5) traduisant l'équilibre des travaux des forces appliquées
3. la formulation variationnelle ou principe de stationnarité:
   c'est un problème d'extremum (de minimisation ou de maximisation suivant le signe de $J(u)$^2.1) (3.7) traduisant à l'équilibre un principe de stationnarité de l'énergie du système.

Suivant les problèmes, l'une ou l'autre formulation peut être la plus appropriée. Cependant l'approximation par éléments finis nécessite l'écriture de la formulation faible ou variationnelle du problème.

2.1.0.1 Remarques

D'un point de vue mathématique, la formulation faible est la formulation la plus générale, car elle s'applique à n'importe quelle équation aux dérivées partielles. Elle permet en outre l'accès à des solutions généralisées (ou solutions faibles) des équations aux dérivées partielles.