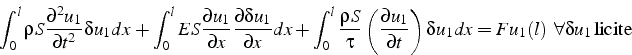2.2 Une seconde approche en dynamique

Considérons maintenant le problème de la vibration libre de la poutre encastrée précédente (figure 3.3 ). L'équation d'équilibre s'écrit:

$$\rho S\frac{\partial^{2}u_{1}}{\partial t^{2}}-\frac{\partial}{\partial x}\left(ES\frac{\partial u_{1}}{\partial x}\right)=0$$ (2.8)

à laquelle on ajoute les conditions aux limites:

$$u_{1}(0,t)=0, ES\frac{\partial u_{1}}{\partial x}(l,t)=0$$ (2.9)

et les conditions initiales (déformée $u_{0}$ à $t=0$ et vitesse initiale nulle):

$$u_{1}(x,0)=u_{0}(x), \frac{\partial u_{1}}{\partial t}=0$$ (2.10)

La formulation faible s'obtient comme précédemment, en multipliant l'équation par un déplacement virtuel licite $\delta u_{1}$ (à un instant t fixé) et en intégrant sur tout le solide:

$$\int_{0}^{l}\rho S\frac{\partial^{2}u_{1}}{\partial t^{2}}\d... ...left(ES\frac{\partial u_{1}}{\partial x}\right)\delta u_{1}dx=0$$

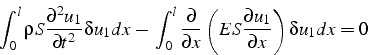
Après intégration par partie du second terme, il vient:

$$\int_{0}^{l}\rho S\frac{\partial^{2}u_{1}}{\partial t^{2}}\d... ...[ES\frac{\partial u_{1}}{\partial x}\delta u_{1}\right]_{0}^{l}$$

En utilisant les conditions aux limites (3.9), la variation $\delta u_{1}$doit s'annuler en $x=0$: $\delta u_{1}(0)=0$ .

$$\int_{0}^{l}\rho S\frac{\partial^{2}u_{1}}{\partial t^{2}}\d... ... u_{1}}{\partial x}\frac{\partial\delta u_{1}}{\partial x}dx=0$$ (2.11)

Cette formulation faible s'écrit:

$$\left\{ \begin{array}{l} \mbox{Trouvez }u_{1}(x,t) \mbox{... ...ta u_{1} \mbox{ t.q. }\delta u_{1}(0)=0\end{array}\right.$$ (2.12)

Dans cette formulation faible, on a considéré une variation $\delta u_{1}(x)$ à un instant t donné. Cette équation traduit l'égalité à chaque instant t du travail des forces d'accélération et des forces élastiques.

Pour écrire la formulation variationnelle, on considéré ce qu'il se passe entre 2 instants: l'instant initial $t=0$ et un instant $t=\tau$. Les 2 positions d'équilibres associées sont notées $u_{1}(x,t=0)$ et $u_{1}(x,t=\tau)$, et on recherche quelles sont les différentes solutions possibles $u(x,t)$ entre ces 2 instants. Les différentes trajectoires (solutions) licites considérées $u(x,t)$coıncident avec les 2 états d'équilibres à $t=0$ et à $t=\tau$:

$$u(x,0)=u_{1}(x,0) \mbox{ et } u(x,\tau)=u_{1}(x,\tau)$$

et vérifient les liaisons $u(0,t)=0$

La variation entre la solution d'équilibre et une de ces trajectoires : $\delta u_{1}=u_{1}(x,t)-u(x,t)$, vérifie donc:

$$\delta u_{1}(x,0)=0, \delta u_{1}(x,\tau)=0$$ (2.13)

et la condition de liaison $\delta u(0,t)=0$.

Pour obtenir la formulation variationnelle, on intègre en temps l'équation (3.11) entre l'instant initial et l'instant $\tau$:

$$\int_{0}^{\tau}\left(\int_{0}^{l}\rho S\frac{\partial^{2}u_{... ...partial x}\frac{\partial\delta u_{1}}{\partial x}dx\right)dt=0$$ (2.14)

En intégrant par partie la dérivée seconde en temps, il vient:

$$\int_{0}^{\tau}\frac{\partial^{2}u_{1}}{\partial t^{2}}\delt... ...\frac{\partial u_{1}}{\partial t}\delta u_{1}\right]_{0}^{\tau}$$

Les conditions imposées sur la variation (3.13) impliquent la nullité du terme de bord, et l'équation (3.14) devient:

$$\int_{0}^{\tau}\delta\left(\frac{1}{2}\int_{0}^{l}\rho S\lef... ...\left(\frac{\partial u_{1}}{\partial x}\right)^{2}dx\right)dt=0$$

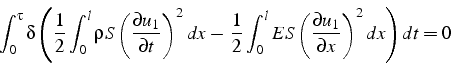
En notant

$$\mathcal{L}(u_{1},\dot{u}_{1})=\underbrace{\frac{1}{2}\int_{... ...{1}}{\partial x}\right)^{2}dx}_{U=\mbox{énergie potentielle}}$$

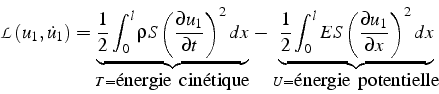
on obtiens:

$$\delta\int_{0}^{\tau}\mathcal{L}(u_{1},\dot{u}_{1}) dt=0$$

Cette relation implique que la solution $u_{1}$ doit être telle que $\mathcal{A}=\int_{0}^{\tau}\mathcal{L}(u_{1},\dot{u}_{1}) dt$ soit extremum. En terme mécanique, cette intégrale représente une action, et la fonctionnelle $\mathcal{L}(u_{1},\dot{u}_{1})$ le Lagrangien du système. En effet la fonctionnelle $\mathcal{L}(u_{1},\dot{u}_{1})=T-U$ est la différence entre l'énergie cinétique $T$ du solide et son énergie potentielle élastique $U$. Elle représente le Lagrangien du système, et l'équation précédente est la traduction du principe de moindre action en mécanique:

“la solution d'équilibre du système $u_{1}(x,t)$ est telle que l'action $\mathcal{A}=\int_{0}^{\tau}\mathcal{L}(u_{1},\dot{u}_{1}) dt$ soit minimum ”.

L'action $\mathcal{A}$ est une fonctionnelle (i.e. est fonction d'une fonction $u_{1}(x,t)$). La condition de minimisation de $\mathcal{A}$ est donc que sa “dérivée par rapport” à $u_{1}$ s'annule (généralisation de la condition d'extremum d'une fonction). La définition de la dérivée fonctionnelle de $\mathcal{A}$ est une généralisation de la dérivée d'une fonction par rapport à une variable, et est fonction de la variation (direction de dérivation) $\delta u_{1}$.

$$<\frac{d\mathcal{A}}{du_{1}},\delta u_{1}>=\lim_{\lambda\rig... ...hcal{A}(u_{1}+\lambda\delta u_{1})-\mathcal{A}(u_{1})}{\lambda}$$

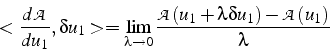
En utilisant cette définition, et en utilisant un calcul classique de variations, la condition de minimisation de l'action conduit aux équations de Lagrange (pour un milieu continu^2.2):

$$<\frac{d}{dt}\left(\frac{\partial\mathcal{L}}{\partial\dot{u... ...„ \delta u_{1}>=0 \forall\delta u_{1} \mbox{ licite}$$ (2.15)

qui correspondent à la formulation faible (3.15), ou principe des travaux virtuels.

A partir de ce formalisme Lagrangien, on peut retrouver les propriétés du système. On définit la quantité $\mathcal{E}(u_{1},\dot{u}_{1})$ par

$$\mathcal{E}(u_{1},\dot{u}_{1})=\frac{\partial\mathcal{L}}{\partial\dot{u}_{1}}\dot{u}_{1}-\mathcal{L}$$

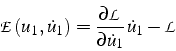
Cette quantité reste constante au cours du temps

$$\mathcal{E}(u_{1},\dot{u}_{1})=cste$$

puisque par définition de $\mathcal{E}(u_{1},\dot{u}_{1})$

$$\begin{eqnarray*} \frac{d}{dt}\mathcal{E}(u_{1},\dot{u}_{1}) & = & \frac{\partia... ...ight)-\frac{\partial\mathcal{L}}{\partial u_{1}}\„ \dot{u}_{1}>\end{eqnarray*}$$

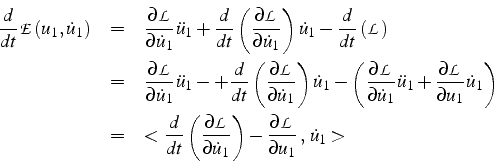
Cette dernière expression est nulle, puisque $\mathcal{L}(u_{1},\dot{u}_{1})$ vérifie les équations de Lagrange (3.15). Cette quantité $\mathcal{E}(u_{1},\dot{u}_{1})=2T-\mathcal{L}=T+U$ est en faite l'énergie totale du système:

$$\mathcal{E}(u_{1},\dot{u}_{1})=\underbrace{\frac{1}{2}\int_{... ...{1}}{\partial x}\right)^{2}dx}_{U=\mbox{énergie potentielle}}$$

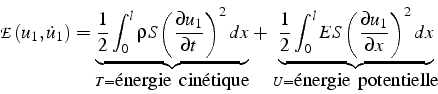
qui se conserve au cours du temps. Pour ce système conservatif, on retrouve donc le principe de conservation de l'énergie.

La formulation variationnelle de notre problème s'écrit:

$$\left\{ \begin{array}{l} \mbox{Trouver }u_{1}(x,t) \mbox{... ...{0}^{\tau}\mathcal{L}(u_{1},\dot{u}_{1}) dt\end{array}\right.$$

La condition de minimisation de l'action conduit aux équations de Lagrange:

$$<\frac{d}{dt}\left(\frac{\partial\mathcal{L}}{\partial\dot{u... ...-\frac{\partial\mathcal{L}}{\partial u_{1}}\„ \delta u_{1}>=0$$

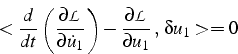
qui correspondent la formulation faible (3.15), ou principe des travaux virtuels

$$\left\{ \begin{array}{l} \mbox{Trouver }u_{1}(x,t) \mbox{... ..._{1}>=0 \forall\delta u_{1} \mbox{licite}\end{array}\right.$$

2.2.1 Élasticité linéaire

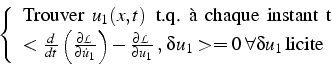
Pour un problème dynamique en élasticité linéaire, utilisant une formulation en déplacement $\overrightarrow{\mathbf{U}}$, le Lagrangien s'écrit sous la forme:

$$\mathcal{L}(\overrightarrow{\mathbf{U}},\overrightarrow{\dot... ...o \overrightarrow{F}.\overrightarrow{\mathbf{U}} ds}_{W_{2}}$$

et comprend l'énergie cinétique $T$, l'énergie potentielle élastique $U$ (qui est le produit tensoriel du tenseur des contraintes et du tenseur des déformations), le travail des forces volumiques externes $\overrightarrow{f}$ et le travail des forces surfaciques externes^2.3 $\overrightarrow{F}$. En utilisant la loi de comportement élastique, et la définition du tenseur des déformations:

$$\overrightarrow{\sigma}=\mathbf{D} \overrightarrow{\varepsi... ...row{\mathbf{gra}}\mathbf{d}^{t} \overrightarrow{\mathbf{U}} )$$

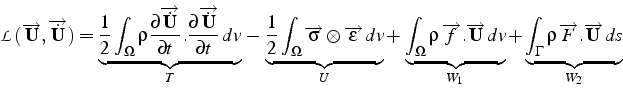
l'énergie élastique s'écrit en fonction du déplacement sous la forme:

$$U=\frac{1}{2}\int_{\Omega}\left(\frac{1}{2}(\overrightarrow{... ...gra}}\mathbf{d}^{t} \overrightarrow{\mathbf{U}} )\right) dv$$

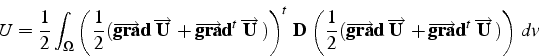
Les équation de Lagrange s'écrivent alors:

$$<\frac{d}{dt}\left(\frac{\partial\mathcal{L}}{\partial\dot{u... ...\partial u_{i}}\„ \delta u_{i}>=0 \mbox{ pour }i=1,3$$

2.2.2 Problème statique

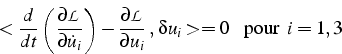
Dans le cas d'un problème statique: $\dot{u}_{1}=\frac{\partial u_{1}}{\partial t}=0$, le Lagrangien ne dépendant que de $u_{1}(x)$, et s'écrit ( en tenant compte du terme de force extérieure $F$):

$$\mathcal{L}(u_{1})=\underbrace{Fu_{1}(l)}_{\mbox{travail d... ...l u_{1}}{\partial x}\right)^{2}dx}_{\mbox{énergie élastique}}$$

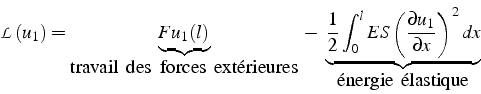
Il correspond donc à l'opposée de la fonctionnelle $J$ (3.6) : $\mathcal{L}(u_{1})=-J(u_{1})$. La formulation faible (3.5) correspond donc bien aux équations de Lagrange à l'équilibre statique:

$$<\frac{\partial\mathcal{L}}{\partial u_{1}}\„ \delta u_{1}>=0 \forall\delta u_{1}$$

2.2.3 Système dynamique amorti

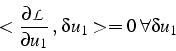
Dans le cas d'un système mécanique amorti, on introduit une force supplémentaire d'amortissement $F_{a}$, en générale dépendant de la vitesse $\dot{u}_{1}$. Cette force n'est pas conservative, et on ne peut plus définir de Lagrangien $\mathcal{L}(u_{1},\dot{u}_{1})$ pour le système complet et écrire les équations de Lagrange (3.15).

En revenant au principe des travaux virtuels, on calcul le travail “virtuel” de la force d'amortissement:

$$\int_{0}^{l}F_{a}(\dot{u}_{1}).\delta u_{1}dx$$

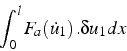
et en utilisant le Lagrangien précédent pour la partie conservative

$$\mathcal{L}(u_{1},\dot{u}_{1})=\frac{1}{2}\int_{0}^{l}\rho S... ...t_{0}^{l}ES\left(\frac{\partial u_{1}}{\partial x}\right)^{2}dx$$

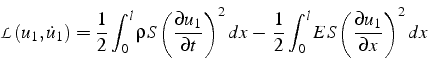
on obtiens les équations de Lagrange généralisées, ou principe des travaux virtuels

$$<\frac{d}{dt}\left(\frac{\partial\mathcal{L}}{\partial\dot{u... ...{u}_{1}).\delta u_{1}dx=0 \forall\delta u_{1} \mbox{licite}$$

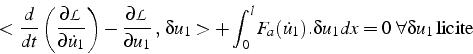
Dans ce cas, on ne peut plus appliquer de principe de moindre action ou formulation variationnelle. On dispose uniquement de la formulation faible, ou principe des travaux virtuels.

2.2.3.1 Exercice 1:

Écrire la formulation faible dans le cas de vibrations forcées induites par une force dépendant du temps $F(t)$ appliquée en $x=l$ .

On pourra montrer que dans ce cas le Lagrangien s'écrit:

$$\mathcal{L}(u_{1},\dot{u}_{1})=\frac{1}{2}\int_{0}^{l}\rho S... ...S\left(\frac{\partial u_{1}}{\partial x}\right)^{2}dx+Fu_{1}(l)$$

2.2.3.2 Exercice 2:

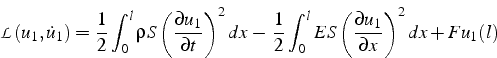
Écrire la formulation faible dans le cas où le système précédent est amorti, avec un amortissement intrinsèque proportionnel à la masse. Dans une section d'épaisseur $dx$ la force d'amortissement s'écrit:

$$-\frac{\rho Sdx}{\tau} \frac{\partial u_{1}}{\partial t}$$

Montrez que les équations de Lagrange s'écrivent:

$$\int_{0}^{l}\rho S\frac{\partial^{2}u_{1}}{\partial t^{2}}\d... ...delta u_{1}dx=Fu_{1}(l) \forall\delta u_{1} \mbox{licite}$$