2.3 Formulation faible en mécanique des fluides

Considérons l'écoulement d'un fluide incompressible très visqueux dans une cavité carrée $\Omega=[0,L]*[0,L]$ dont la partie supérieure est mise en mouvement (figure 3.4). Par entraınement visqueux, le fluide se met en mouvement dans la cavité pour former un tourbillon.

Figure 3.2: écoulement dans une cavité

En considérant le problème comme plan, les équations d'équilibre sont les équations de Stockes:

$$\frac{\partial v_{1}}{\partial x}+\frac{\partial v_{2}}{\partial y} = 0$$ (2.16)

$$-\frac{\mu}{\rho}\left(\frac{\partial^{2}v_{1}}{\partial x^{2}}+\frac{\partial^{2}v_{1}}{\partial y^{2}}\right) = -\frac{1}{\rho}\frac{\partial p}{\partial x}$$ (2.17)

$$-\frac{\mu}{\rho}\left(\frac{\partial^{2}v_{2}}{\partial x^{2}}+\frac{\partial^{2}v_{2}}{\partial y^{2}}\right) = -\frac{1}{\rho}\frac{\partial p}{\partial y}$$ (2.18)

auxquels on ajoute les conditions aux limites d'adhérence aux parois:

$$\overrightarrow{\mathbf{V}}(x,L)=[V_{0},0], \overrigh... ...)=\overrightarrow{\mathbf{V}}(L,y)=\overrightarrow{\mathbf{0}}$$ (2.19)

Pour écrire la formulation faible de ce système on considère à un instant t une variation de vitesse $\delta\overrightarrow{\mathbf{V}}$ . Cette variation doit être licite, i.e. si on fixe la valeur de la vitesse (condition de Dirichlet), la variation s'annule (condition de Dirichlet homogène):

$$\delta\overrightarrow{\mathbf{V}}(x,L)=\delta\overrightarrow... ...ta\overrightarrow{\mathbf{V}}(L,y)=\overrightarrow{\mathbf{0}}$$ (2.20)

Les équations d'équilibre (3.17,3.18) sont la projection de l'équation vectorielle:

$$-\frac{\mu}{\rho} \overrightarrow{\mathbf{div}}\left(\overr... ... \overrightarrow{\mathbf{V}}\right)=-\overrightarrow{grad} p$$

que nous multiplions donc scalairement par $\delta\overrightarrow{\mathbf{V}}$ et intégrons sur le domaine $\Omega$pour obtenir la puissance virtuelle des forces appliquées pour une variation $\delta\overrightarrow{\mathbf{V}}$ de la vitesse:

$$-\int_{\Omega}\frac{\mu}{\rho} \overrightarrow{\mathbf{div}... ...tarrow{grad} p\bullet\delta\overrightarrow{\mathbf{V}} dxdy$$

En intégrant par partie les 2 termes il vient:

$$\begin{eqnarray*} \int_{\Omega}\frac{\mu}{\rho} \overrightarrow{\mathbf{grad}}\... ...errightarrow{n}\bullet\delta\overrightarrow{\mathbf{V}} d\Gamma\end{eqnarray*}$$

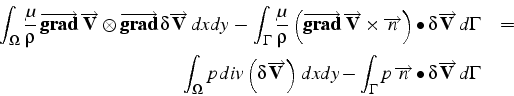
En utilisant les conditions(3.20) imposées à $\delta\overrightarrow{\mathbf{V}}$: $\left(\delta\overrightarrow{\mathbf{V}}\right)_{\Gamma}=\overrightarrow{0}$, les intégrales de bord s'annulent et il reste:

$$\int_{\Omega}\frac{\mu}{\rho} \overrightarrow{\mathbf{grad}... ...a}p div\left(\delta\overrightarrow{\mathbf{V}}\right) dxdy$$ (2.21)

2.3.1 Première formulation faible du problème de Stockes

Si on impose de plus à la variation $\delta\overrightarrow{\mathbf{V}}$ d'être incompressible: $div \delta\overrightarrow{\mathbf{V}}=0$, on obtiens une première formulation faible du problème:

$$% latex2html id marker 2034\left\{ \begin{array}{c} \mbox{... ...hbf{V}}=0 \mbox{ et (\ref{chap2:eq24})}\end{array}\right.$$ (2.22)

L'équation intégrale projetée sur les 2 axes $(ox,oy)$ s'écrit aussi:

$$\begin{eqnarray*} \int_{\Omega}\frac{\mu}{\rho} \left(\frac{\partial v_{1}}{\pa... ...a v_{2}}{\partial y}\right) dxdy & = & 0 \forall\delta v_{2}\end{eqnarray*}$$

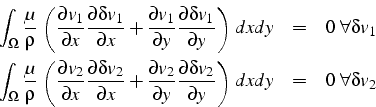
Cette formulation faible traduit le fait que la somme des puissances des forces visqueuses doit être nulle pour toute variation de vitesse $\delta\overrightarrow{\mathbf{V}}$ licite et incompressible . On constate que la pression n'intervient plus dans cette formulation, puisque que la puissance des forces de pression est automatiquement nulle pour une variation de vitesse $\delta\overrightarrow{\mathbf{V}}$ licite et incompressible. On retrouve l'interprétation classique du champ de pression dans un écoulement de fluide incompressible: la pression $p$ sert à maintenir le champ de vitesse incompressible ( i.e. $div \overrightarrow{\mathbf{V}}=0$). Dans la formulation variationnelle (3.22), on impose au champ de vitesse et à sa variation de rester incompressible, et donc on élimine la pression du problème. On constate que l'élimination de la pression a aussi découplée les équations de vitesse. Attention cependant, ce découplage n'est que relatif, puisque la condition d'incompressibilité couple les composantes de vitesse.

Cette formulation faible découle d'un problème variationnelle, puisque pour ce problème on peut définir un Lagrangien:

$$\mathcal{L}(v_{1},v_{2})=\frac{1}{2}\int_{\Omega}\frac{\mu}{... ...left(\frac{\partial v_{2}}{\partial y}\right)^{2}\right) dxdy$$

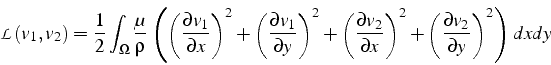
Le champ de vitesse solution minimise ce Lagrangien $\mathcal{L}(v_{1},v_{2})$, qui n'est autre que l'énergie dissipée sous forme visqueuse. La solution du problème de Stokes (3.16,3.17,3.18) est donc le champ de vitesse incompressible vérifiant les conditions aux limites (3.19) qui minimise la dissipation visqueuse.

La formulation faible correspond alors aux équations de Lagrange:

$$\begin{eqnarray*} <\frac{\partial\mathcal{L}}{\partial v_{1}}\„ \delta v_{1}> ... ...ac{\partial\mathcal{L}}{\partial v_{2}}\„ \delta v_{2}> & = & 0\end{eqnarray*}$$

2.3.2 Seconde formulation faible du problème de Stockes

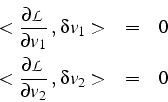
Si on n'impose pas à la variation du champ de vitesse d'être incompressible, la formulation intégrale (3.21) contient un terme de pression $p$. Il faut donc tenir compte d'une variation $\delta p$de ce champ de pression, qui doit être tel que le champ de vitesse $\overrightarrow{\mathbf{V}}$ reste incompressible . Il faut donc multiplier l'équation (3.16) (qui est la condition d'incompressibilité $div \overrightarrow{\mathbf{V}}=0$) par $\delta p$ et intégrer sur le domaine:

$$\int_{\Omega}\delta p div \overrightarrow{\mathbf{V}} dxdy=0$$

On remarque que c'est le terme symétrique de l'intégrale de pression dans (3.21), et qui traduit le fait que la puissance de toute variation de pression $\delta p$calculée pour le champ de vitesse $\overrightarrow{\mathbf{V}}$ doit être nulle.

La formulation faible de (3.16,3.17,3.18) s'écrit donc

$$% latex2html id marker 13791\left\{ \begin{array}{c} \mbox... ...\delta p \mbox{ t.q. (\ref{chap2:eq24})}\end{array}\right.$$

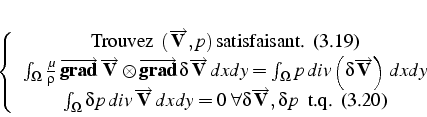
Cette formulation correspond aussi à un problème variationnel dont le Lagrangien s'écrit:

$$\begin{eqnarray*} \mathcal{L}(v_{1},v_{2},p) & = & \frac{1}{2}\int_{\Omega}\frac... ...l v_{1}}{\partial x}+\frac{\partial v_{2}}{\partial y}\right)dxdy\end{eqnarray*}$$

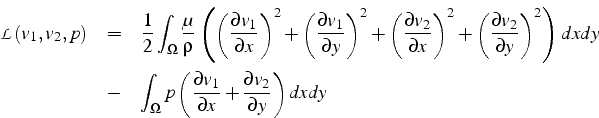
et les équations de Lagrange:

$$\begin{eqnarray*} <\frac{\partial\mathcal{L}}{\partial v_{1}}\„ \delta v_{1}> ... ...\\ <\frac{\partial\mathcal{L}}{\partial p}\„ \delta p> & = & 0\end{eqnarray*}$$

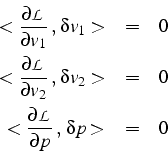
Dans le Lagrangien, on remarque que la contrainte $div\overrightarrow{ \mathbf{V}}=0$ est multipliée par la pression. La pression apparaıt donc comme le multiplicateur de Lagrange de la contrainte d'incompressibilité.

Dans la pratique, nous utiliserons plutôt la seconde formulation dans laquelle la contrainte est imposée explicitement à travers la pression, car elle est en générale plus simple à approximer numériquement. Cependant certaines méthodes numériques utilisent la première formulation.

2.3.3 Problème instationnaire

Pour le problème de Navier-Stockes avec des termes instationnaires, on applique le principe des puissances virtuelles pour obtenir la formulation faible des équations. Par contre, cette formulation n'est plus associée à une formulation variationnelle, puisque que l'on ne peut pas définir de Lagrangien.