suivant: 2.5 Formulation faible discrète monter: 2. Formulation faible et précédent: 2.3 Formulation faible en Table des matières
Nous avons vu dans les exemples précédents que la formulation faible peut être obtenue à partir de principes mécaniques (principe des travaux virtuels, principe des puissances virtuelles), d'une formulation lagrangienne (pour des systèmes conservatifs). En fait cette formulation faible peut s'appliquer à n'importe quel système d'équations aux dérivées partielles en utilisant une généralisation de l'approche qui utilise l'analyse fonctionnelle.
C'est cette approche que nous présentons sur l'exemple de l'équation
de la chaleur stationnaire avec un second membre ![]() :
:
et les conditions aux limites:
La démarche est la suivante:
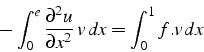
![\begin{displaymath}
\int_{0}^{1}\frac{\partial u}{\partial x}\frac{\partial v}{\...
...ac{\partial u}{\partial x}v\right]_{0}^{1}=\int_{0}^{1}f.v dx\end{displaymath}](img386.png)
![\begin{displaymath}
\left[\frac{\partial u}{\partial x}v\right]_{0}^{1}=0-0=0\end{displaymath}](img388.png)
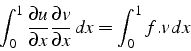
De même les fonctions, dont la dérivée est de carré sommable, forment
un espace vectoriel de Hilbert
![]() . Cet espace
contiens l'espace des fonctions à dérivées continues
. Cet espace
contiens l'espace des fonctions à dérivées continues
![]() ,
mais est bien plus vaste.
,
mais est bien plus vaste.
La formulation faible s'écrit alors:
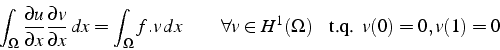
D'un point de vue mathématique et numérique, cette formulation (3.26)
a de nombreux avantages par rapport à l'équation aux dérivées partielles
(3.23). En particulier les conditions de régularité imposées
sur la solution moins contraignantes dans (3.26) avec
une solution dans ![]() , que dans (3.23) avec
une solution dans
, que dans (3.23) avec
une solution dans
![]() . Cela permet d'une part
de calculer des solutions généralisées (i.e. qui ne sont pas dans
. Cela permet d'une part
de calculer des solutions généralisées (i.e. qui ne sont pas dans
![]() ), et d'autre part la construction plus
simple d'approximations de la solution (qui seront dans
), et d'autre part la construction plus
simple d'approximations de la solution (qui seront dans ![]() même si la solution est dans
même si la solution est dans
![]() ).
).
Cette formulation faible a été obtenue par une généralisation du principe
des travaux ou puissances virtuelles. En notant
![]() l'espace des fonctions
l'espace des fonctions ![]() de
de ![]() telles que
telles que
![]() ,
elle s'écrit:
,
elle s'écrit:
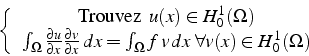
soit en utilisant le produit scalaire (3.25)
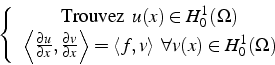
On peut donner une interprétation de cette formulation. Notons symboliquement l'équation aux dérivée partielle (3.23) (associée aux conditions aux limites (3.24)):
Le résidu de cette équation s'écrit pour une fonction ![]() :
:
La formulation faible consiste à écrire que pour la solution ![]() ,
le résidu
,
le résidu ![]() doit être orthogonal au sens du produit scalaire
(3.25) à l'espace des fonctions tests
doit être orthogonal au sens du produit scalaire
(3.25) à l'espace des fonctions tests ![]()
En intégrant par partie, on symétrise ce produit scalaire, pour obtenir
une forme bilinéaire
![]() .
L'équation finale s'écrit donc
.
L'équation finale s'écrit donc
Un théorème mathématique (Lax Milgram) permet alors de montrer l'unicité
de la solution ![]() , qui est la projection dans
, qui est la projection dans
![]() de la forme linéaire
de la forme linéaire
![]() .
.
Si la forme bilinéaire ![]() est symétrique et V-elliptique (i.e.
définie positive), cette forme bilinéaire est un produit scalaire
dans
est symétrique et V-elliptique (i.e.
définie positive), cette forme bilinéaire est un produit scalaire
dans
![]() , et le problème correspond à un problème
de minimisation d'une fonctionnelle
, et le problème correspond à un problème
de minimisation d'une fonctionnelle
![]() dans
dans
![]() .
Pour notre problème:
.
Pour notre problème:
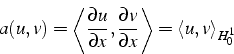
et la fonctionnelle
![]() s'écrit:
s'écrit:
Cette fonctionnelle est bien minimale en ![]() . En effet, en posant
. En effet, en posant
![]()
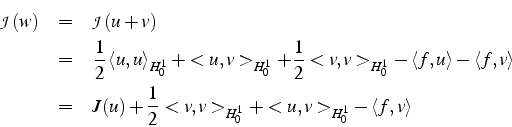
et en utilisant (3.27), il vient
Cette fonctionnelle ![]() est le Lagrangien du système (au signe
près) , et on retrouve la formulation variationnelle:
est le Lagrangien du système (au signe
près) , et on retrouve la formulation variationnelle:
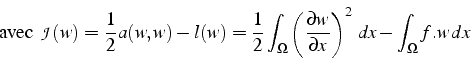
Pour ce problème, on peut calculer la valeur de la fonctionnelle ![]() à l'équilibre, en choisissant comme fonction test
à l'équilibre, en choisissant comme fonction test ![]() la solution
la solution
![]() dans la formulation faible.
dans la formulation faible.
d'où