suivant: 3. Méthode des éléments monter: 2. Formulation faible et précédent: 2.4 Formulation faible: approche Table des matières
Nous avons vue qu'il existait plusieurs approches (travaux virtuels,
Lagrange, approche formelle) pour obtenir la formulation faible d'une
équation (ou système d'équations) aux dérivées partielles ![]() .
.
Cette formulation faible peut s'écrire sous la forme symbolique:
où ![]() est l'espace des solutions,
est l'espace des solutions, ![]() la forme bilinéaire associée
aux dérivées partielles de l'équation et
la forme bilinéaire associée
aux dérivées partielles de l'équation et ![]() la forme linéaire
associée au second membre.
la forme linéaire
associée au second membre.
L'espace des solutions ![]() est un espace de fonctions (de dimension
infinie), et la recherche d'une solution analytique de (3.29)
dans cet espace n'est en générale pas possible.
est un espace de fonctions (de dimension
infinie), et la recherche d'une solution analytique de (3.29)
dans cet espace n'est en générale pas possible.
On recherche donc une solution approchée ![]() , en construisant
une approximation
, en construisant
une approximation ![]() de dimension finie
de dimension finie ![]() de l'espace des
solutions
de l'espace des
solutions ![]() . On se donne pour cela une famille libre de
. On se donne pour cela une famille libre de ![]() fonctions
fonctions
![]() de
de ![]() , et on construit l'espace
vectoriel
, et on construit l'espace
vectoriel ![]() engendré par ces
engendré par ces ![]() fonctions:
fonctions:
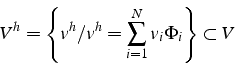
On cherche alors la solution de la formulation dans cette espace ![]() ,
en résolvant le problème discret:
,
en résolvant le problème discret:
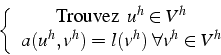
En décomposant la solution ![]() sur la base des fonctions
sur la base des fonctions ![]()
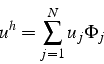
et en prenant comme fonction test ![]() chacune des fonctions de
base
chacune des fonctions de
base ![]() (ce qui est équivalent), la formulation faible s'écrit,
en tenant de la bilinéarité de
(ce qui est équivalent), la formulation faible s'écrit,
en tenant de la bilinéarité de ![]()
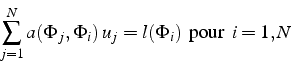
qui n'est autre qu'un système linéaire d'ordre ![]()
qu'il suffit de résoudre pour obtenir la solution approchée ![]() .
.
Si le problème admet une formulation variationnelle, la solution ![]() minimise la fonctionnelle
minimise la fonctionnelle ![]() dans
dans ![]() :
:
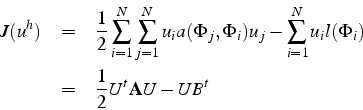
![]() est une fonction quadratique de
est une fonction quadratique de ![]() variables
variables
![]() , qui est minimum si le gradient de
, qui est minimum si le gradient de
![]() par
rapport à ces
par
rapport à ces ![]() variables est nul. Or
variables est nul. Or
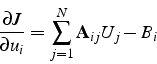
et la condition de minimisation conduit alors au système linéaire (3.30).
La méthode des éléments finis n'est qu'une méthode particulière pour
construire l'espace ![]() et les fonctions de base
et les fonctions de base ![]() .
.
Pour terminer, nous allons donner quelques propriétés de la formulation faible discrète.
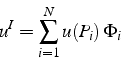
Considérons le problème (3.23, 3.24) avec
![]() .La solution analytique
.La solution analytique ![]() est le polynôme du second
degré:
est le polynôme du second
degré:
La fonctionnelle
![]() de la formulation variationnelle
(3.28) s'écrit:
de la formulation variationnelle
(3.28) s'écrit:
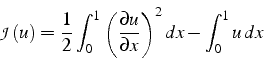
et un calcul directe fournit:
Nous allons calculer une approximation de cette solution exacte sur
une base de fonctions trigonométriques. Compte tenu des conditions
aux limites et des propriétés de symétrie du problème par rapport
à ![]() , les fonctions choisies sont les fonctions de base
, les fonctions choisies sont les fonctions de base ![]() :
:
Et nous allons calculer la solution approchée ![]() en utilisant
que deux fonctions de base
en utilisant
que deux fonctions de base ![]() et
et ![]()
On peut alors calculer
![]() analytiquement (en utilisant
Maple par exemple)
analytiquement (en utilisant
Maple par exemple)
Cette fonctionnelle est un paraboloıde de révolution (représenté sur la figure 3.3), dont le minimum est obtenu par résolution du système d'équations:
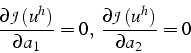
Ces équations s'écrivent:
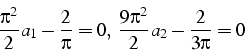
Ces équations sont identiques à celles obtenues avec la formulation
faible (3.26), en remplaçant la solution exacte ![]() par son approximation
par son approximation ![]() , et les fonctions tests
, et les fonctions tests ![]() par les
fonctions de base
par les
fonctions de base ![]() et
et ![]() 2.5. Ce système d'équations linéaires permet de déterminer les coefficients
inconnus
2.5. Ce système d'équations linéaires permet de déterminer les coefficients
inconnus
![]() .
.
La solution approchée ![]() s'écrit:
s'écrit:
On a tracé sur la figure 3.4 la solution approchée ![]() comparée à la solution exacte
comparée à la solution exacte ![]() , ainsi que l'erreur d'approximation
, ainsi que l'erreur d'approximation
![]() . On constate sur la figure que l'on a une très bonne
approximation de la solution, avec une erreur uniformément répartie
(de l'ordre de
. On constate sur la figure que l'on a une très bonne
approximation de la solution, avec une erreur uniformément répartie
(de l'ordre de ![]() maximum).
maximum).
Pour cette solution approchée ![]() , la valeur de la fonctionnelle
, la valeur de la fonctionnelle
![]() vaut:
vaut:
qui est légèrement plus grande que la valeur exacte (3.31).
Nous allons maintenant montrer que la solution approchée ![]() calculée avec la formulation faible discrète est la meilleure approximation2.6 de la solution exacte
calculée avec la formulation faible discrète est la meilleure approximation2.6 de la solution exacte ![]() du problème dans l'espace d'approximation
du problème dans l'espace d'approximation
![]() engendré par les fonctions de base
engendré par les fonctions de base ![]() et
et ![]() .
.
Pour cela nous allons tout d'abord comparer ![]() à l'interpolation
à l'interpolation
![]() dans
dans ![]() de la solution exacte
de la solution exacte ![]() aux 5 points
d'interpolations
aux 5 points
d'interpolations
![]() .
Cette interpolation de
.
Cette interpolation de ![]() s'écrit:
s'écrit:
et coıncide avec la solution exacte aux points d'interpolation ![]() :
:
Compte tenu des propriétés de symétrie du problème, ces 5 relations ne donnent que 2 équations indépendantes;
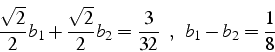
qui permettent la détermination unique des coefficients ![]() et
et
![]() . L'interpolation
. L'interpolation ![]() s'écrit donc:
s'écrit donc:
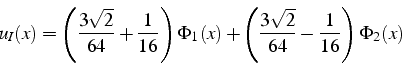
Cette solution approxime bien la solution exacte ![]() , comme
on peut le constater sur la figure 3.5, mais l'erreur
d'interpolation est plus grande en moyenne que l'erreur d'approximation
comme on le constate sur cette même figure.
, comme
on peut le constater sur la figure 3.5, mais l'erreur
d'interpolation est plus grande en moyenne que l'erreur d'approximation
comme on le constate sur cette même figure.
Pour le vérifier, on calcule l'erreur moyenne (en norme
![]() ):
):
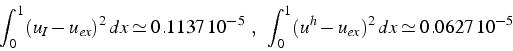
et constate donc que l'erreur d'approximation est plus faible que
l'erreur d'interpolation, et donc la solution ![]() est meilleure
que l'interpolation
est meilleure
que l'interpolation ![]() .
.
De façon plus générale, si l'on cherche la fonction ![]() de
de ![]() qui minimise l'erreur d'approximation (au sens de la norme
qui minimise l'erreur d'approximation (au sens de la norme
![]() ):
):
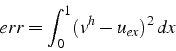
on retrouve l'approximation ![]() .
.
De même, si l'on cherche la fonction ![]() de
de ![]() qui minimise
l'erreur d'approximation (au sens de la norme associée à la fonctionnelle
qui minimise
l'erreur d'approximation (au sens de la norme associée à la fonctionnelle
![]() )
)
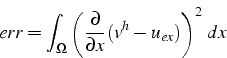
on retrouve encore l'approximation ![]() . En fait la minimisation
de cette erreur conduit à la formulation faible discrète, d'où le
résultat.
. En fait la minimisation
de cette erreur conduit à la formulation faible discrète, d'où le
résultat.