suivant: 5.2 Éléments finis triangulaire monter: 5. Méthodes des éléments précédent: 5. Méthodes des éléments Table des matières
On considère l'écoulement incompressible à potentiel dans un canal bidimensionnel obturé partiellement par un obstacle carré. Les dimensions du problème sont indiquées sur la figure (6.1).
L'équation d'équilibre régissant la fonction de courant ![]() n'est autre que l'équation de Laplace
n'est autre que l'équation de Laplace
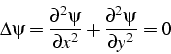
où ![]() est la fonction de courant telle que:
est la fonction de courant telle que:
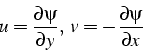
![]() et
et ![]() étant les composantes de la vitesse. Les conditions aux
limites en vitesse pour ce problème sont:
étant les composantes de la vitesse. Les conditions aux
limites en vitesse pour ce problème sont:
La formulation faible du problème s'obtiens en multipliant l'équation
par une fonction test ![]() , et en intégrant sur le domaine
, et en intégrant sur le domaine ![]() . En utilisant la formule de Green, on intègre par partie le terme
en Laplacien pour tenir compte des conditions aux limites et symétriser
le problème. En utilisant les conditions aux limites, et en interprétant
la fonction test
. En utilisant la formule de Green, on intègre par partie le terme
en Laplacien pour tenir compte des conditions aux limites et symétriser
le problème. En utilisant les conditions aux limites, et en interprétant
la fonction test ![]() comme une variation
comme une variation ![]() de la
solution
de la
solution ![]() , la formulation faible s'écrit:
, la formulation faible s'écrit:
Dans la suite, pour effectuer les calculs, nous choisirons comme valeurs
numériques ![]() et
et
![]() , ce qui impose un débit
unité en entrée.
, ce qui impose un débit
unité en entrée.
La formulation faible (6.1) est équivalente à la formulation variationnelle suivante:
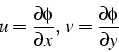
L'équation de continuité
![]() impose à ce
potentiel de vérifier l'équation de Laplace:
impose à ce
potentiel de vérifier l'équation de Laplace:
Le potentiel ![]() et la fonction de courant
et la fonction de courant ![]() vérifient donc
la même équation, mais avec des conditions aux limites différentes.
vérifient donc
la même équation, mais avec des conditions aux limites différentes.
Exercice: montrez que ce sont deux familles de fonctions
orthogonales, i.e. les courbes potentiel ![]() sont perpendiculaires
aux lignes de courant.
sont perpendiculaires
aux lignes de courant.
Les conditions aux limites sur le potentiel ![]() sont:
sont:
La fonctionnelle ![]() a une interprétation physique: c'est l'énergie
cinétique totale:
a une interprétation physique: c'est l'énergie
cinétique totale:
La solution à potentiel du problème (6.3) et donc (6.1) correspond donc au champ de vitesse qui minimise l'énergie cinétique globale parmi tous les champs de vitesse à potentiel vérifiant les conditions aux limites. Cette propriété, caractéristique des écoulements incompressibles à potentiel (ou irrotationnels), a été découverte par Lord Kelvin en 1849 5.1.
Exercice: démontrer cette propriété.
Pour résoudre numériquement le problème (6.1), on cherche
une solution approchée ![]() . En éléments finis cette solution
est définie par la donnée:
. En éléments finis cette solution
est définie par la donnée:
La description d'un maillage comprend deux informations principales:
|
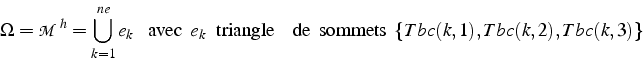
Sur chaque élément ![]() du maillage, l'approximation
du maillage, l'approximation ![]() par élément finis
par élément finis
![]() d'une fonction
d'une fonction ![]() est
un polynôme de degré 1 en
est
un polynôme de degré 1 en ![]() et
et ![]() , qui s'écrit:
, qui s'écrit:
Pour déterminer ce polynôme, il faut 3 points d'interpolation
![]() et la valeur de la fonction
et la valeur de la fonction
![]() en ces
3 points. Les 3 équations
en ces
3 points. Les 3 équations
![]() permettent
alors de déterminer les 3 coefficients de
permettent
alors de déterminer les 3 coefficients de
![]() . Pour
assurer la condition de continuité globale de la solution, on choisit
comme points d'interpolation les 3 sommets
. Pour
assurer la condition de continuité globale de la solution, on choisit
comme points d'interpolation les 3 sommets
![]() du triangle
du triangle ![]() . L'approximation est donc définie par ses valeurs
aux
. L'approximation est donc définie par ses valeurs
aux ![]() noeuds du maillage.
noeuds du maillage.
Considérons par exemple la fonction
![]() sur le maillage (6.2). Elle est définie par le tableau de
valeurs nodales
sur le maillage (6.2). Elle est définie par le tableau de
valeurs nodales ![]() suivants:
suivants:
Sur l'élément 5 qui a pour sommets les noeuds
La résolution du système (6.4) permet d'obtenir les expressions
suivantes pour ![]()
Les relations (6.5) montrent que l'interpolation
![]() de
de ![]() sur l'élément
sur l'élément ![]() (
(
![]() ) est une combinaison
linéaire des valeurs nodales
) est une combinaison
linéaire des valeurs nodales
![]() ,
qui s'écrit:
,
qui s'écrit:
Les fonctions
![]() sont
les 3 polynômes de degré 1, associés aux 3 sommets
sont
les 3 polynômes de degré 1, associés aux 3 sommets
![]() de l'élément, suivants:
de l'élément, suivants:
Ces polynômes de degré 1 (dont on vérifie les symétries par permutation d'indices) vérifient :
Ainsi le polynôme ![]() vaut 1 sur le sommet
vaut 1 sur le sommet ![]() et 0
sur les 2 autres sommets
et 0
sur les 2 autres sommets ![]() et
et ![]() ; de même pour
; de même pour ![]() et
et ![]() avec une permutation des indices. La représentation
en perspective de ces 3 fonctions est donnée sur la figure (6.4)
(pour le tracé on a remplacer les coordonnées des sommets par leurs
valeurs obtenues dans le tableau 6.1: i.e.
avec une permutation des indices. La représentation
en perspective de ces 3 fonctions est donnée sur la figure (6.4)
(pour le tracé on a remplacer les coordonnées des sommets par leurs
valeurs obtenues dans le tableau 6.1: i.e.
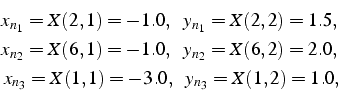
Ces polynômes vérifient en outre la relation:
Dans le cas d'une interpolation
![]() , ces polynômes
ont une interprétation géométrique. Ce sont les coordonnées barycentriques.
Ces coordonnées sont définies de la façon suivante: pour chaque point
, ces polynômes
ont une interprétation géométrique. Ce sont les coordonnées barycentriques.
Ces coordonnées sont définies de la façon suivante: pour chaque point
![]() de coordonnées
de coordonnées ![]() , le vecteur
, le vecteur
![]() s'écrit
en fonction des sommets du triangle, comme combinaison des vecteurs
s'écrit
en fonction des sommets du triangle, comme combinaison des vecteurs
![]() ,
,
![]() ,
,
![]() .
Les coefficients sont les coordonnées barycentriques par rapport au
triangle considéré, i.e.
.
Les coefficients sont les coordonnées barycentriques par rapport au
triangle considéré, i.e.
Les valeurs de
![]() vérifient les
relations (voir la figure 6.5 pour les notations):
vérifient les
relations (voir la figure 6.5 pour les notations):
qui sont justement les expressions (6.7) des polynômes
![]() .
.
Exercice: démontrer ces relations
On a aussi une propriété remarquable des coordonnées barycentriques:
un point ![]() est à l'intérieur du triangle si et seulement si ses
3 coordonnées barycentriques sont positives, il est sur un des cotés
du triangle si la coordonnée barycentrique par rapport au coté opposé
est nulle, et il est à l'extérieur du triangle si une au moins des
coordonnées barycentriques est négative.
est à l'intérieur du triangle si et seulement si ses
3 coordonnées barycentriques sont positives, il est sur un des cotés
du triangle si la coordonnée barycentrique par rapport au coté opposé
est nulle, et il est à l'extérieur du triangle si une au moins des
coordonnées barycentriques est négative.
L'approximation par éléments finis est donc définie de façon locale
sur chaque élément, en calculant des formules d'interpolation du type
(6.6) et (6.7). De façon a obtenir une expression
générique pour l'interpolation, on va, comme dans le chapitre précédent
introduire une transformation d'un élément ![]() vers un élément
de référence. Cet élément de référence est le triangle rectangle unité
dans le plan de référence
vers un élément
de référence. Cet élément de référence est le triangle rectangle unité
dans le plan de référence ![]() (figure 6.6).
(figure 6.6).
Cette transformation
dont l'expression de ![]() en fonction de
en fonction de ![]() s'écrit
:
s'écrit
:
![\begin{displaymath}
\left[\begin{array}{c}
\xi\\
\eta\end{array}\right]=\left[\...
...\right]+\left[\begin{array}{c}
b_{1}\\
b_{2}\end{array}\right]\end{displaymath}](img1154.png)
Les 6 coefficients de la transformation sont déterminés par les conditions
de transformation des 3 sommets
![]() de
de ![]() vers les 3 sommets
vers les 3 sommets
![]() de l'élément de référence
de l'élément de référence
![]() :
:
On remarque que ![]() est un polynôme de degré 1 en
est un polynôme de degré 1 en ![]() ,
qui vaut 0 en
,
qui vaut 0 en ![]() (car
(car
![]() ) , 1 en
) , 1 en ![]() (car
(car
![]() ), et 0 en
), et 0 en ![]() (car
(car
![]() ).
C'est donc le polynôme d'interpolation
).
C'est donc le polynôme d'interpolation ![]() (ou la coordonnée
barycentrique
(ou la coordonnée
barycentrique
![]() ) associé au sommet
) associé au sommet ![]() , dont
l'expression est donnée en (6.7). De même
, dont
l'expression est donnée en (6.7). De même ![]() est
un polynôme de degré 1 en
est
un polynôme de degré 1 en ![]() , qui vaut 0 en
, qui vaut 0 en ![]() (car
(car
![]() ),
0 en
),
0 en ![]() (car
(car
![]() ), et 1 en
), et 1 en ![]() (car
(car
![]() ). C'est donc le polynôme d'interpolation de
Lagrange
). C'est donc le polynôme d'interpolation de
Lagrange![]() (ou la coordonnée barycentrique
(ou la coordonnée barycentrique
![]() )
associé au sommet
)
associé au sommet ![]() . On a donc:
. On a donc:
et
En notant
![]() les coordonnées du sommet
les coordonnées du sommet ![]() de l'élément
de l'élément ![]() , on obtiens l'expression générique de la transformation
de
, on obtiens l'expression générique de la transformation
de ![]() vers l'élément de référence
vers l'élément de référence ![]() :
:
Sur cet élément de référence, les 3 polynômes d'interpolation
![]() ont une expression très simple: ce sont les fonctions forme
ont une expression très simple: ce sont les fonctions forme
![]() de l'approximation
de l'approximation
![]() sur l'élément de référence associées
aux 3 sommets
sur l'élément de référence associées
aux 3 sommets
![]() :
:
Exercice: montrer qu'en écrivant ces relations (6.13) en variable (x,y) on retrouve la relation (6.8) sur les coordonnées barycentriques.
La matrice jacobienne
![]() =
=
![]() de cette transformation se calcule simplement:
de cette transformation se calcule simplement:
De même la matrice jacobienne de la transformation inverse
![]() est égale à l'inverse de
est égale à l'inverse de
![]() :
:
en notant
![]() l'aire du triangle
l'aire du triangle ![]()
En notant
![]() les numéros des 3 sommets de l'élément
les numéros des 3 sommets de l'élément
![]() qui sont donnés par la table de connection (
qui sont donnés par la table de connection (
![]() ,
,
![]() ,
,
![]() ), l'approximation
), l'approximation ![]() s'écrit
sur l'élément
s'écrit
sur l'élément ![]() :
:
Cette expression a la même forme que la relation (6.6), mais l'expression (6.12) des fonctions de forme est beaucoup plus simple que l'expression (6.7) des polynômes d'interpolation, ce qui va nous permettre en particulier un calcul plus simple des intégrales dans la formulation faible.
Attention: la dérivée d'une fonction dans l'élément
de référence n'est évidemment pas égale à la dérivée dans le plan
physique ![]() . Il faut tenir compte du changement de variable:
. Il faut tenir compte du changement de variable:
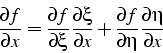
qui s'écrit en fonction de la transposée de l'inverse de la
matrice jacobienne
![]() . Le vecteur gradient s'écrit:
. Le vecteur gradient s'écrit:
Nous avons montré que l'approximation ![]() par éléments finis
par éléments finis
![]() d'une fonction
d'une fonction ![]() sur le maillage (6.2)
était déterminée par les valeurs nodales
sur le maillage (6.2)
était déterminée par les valeurs nodales ![]() de
de
![]() aux
aux ![]() noeuds
noeuds ![]() du maillage. Sur chaque élément,
du maillage. Sur chaque élément,
![]() est un polynôme de degré 1 donnée par l'expression (6.16),
qui est une fonction linéaire des 3 valeurs aux sommets de l'élément.
est un polynôme de degré 1 donnée par l'expression (6.16),
qui est une fonction linéaire des 3 valeurs aux sommets de l'élément.
On peut donc écrire l'approximation ![]() comme une combinaison
linéaire des valeurs nodales
comme une combinaison
linéaire des valeurs nodales
![]() :
:
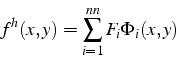
Les fonctions ![]() sont les fonctions de base de l'approximation.
Elles sont telles que sur chaque élément
sont les fonctions de base de l'approximation.
Elles sont telles que sur chaque élément ![]() on retrouve l'approximation
(6.16), ce sont donc des polynômes de degré 1 en
on retrouve l'approximation
(6.16), ce sont donc des polynômes de degré 1 en ![]() .
De plus elles vérifient la propriété suivante pour chaque noeud
.
De plus elles vérifient la propriété suivante pour chaque noeud ![]() du maillage de coordonnées
du maillage de coordonnées ![]() :
:
Autrement dit la fonction de base ![]() est une fonction
continue qui vaut 1 au noeud
est une fonction
continue qui vaut 1 au noeud ![]() du maillage, 0 sur tout les autres
noeuds, et qui sur chaque élément est un polynôme de degré 1. On en
déduit que sur un élément
du maillage, 0 sur tout les autres
noeuds, et qui sur chaque élément est un polynôme de degré 1. On en
déduit que sur un élément ![]() dont le noeud
dont le noeud ![]() n'est pas un
sommet, la fonction
n'est pas un
sommet, la fonction ![]() est identiquement nulle (car
elle est nulle sur les trois sommets). Le support de la fonction
est identiquement nulle (car
elle est nulle sur les trois sommets). Le support de la fonction ![]() (i.e. le lieu des points où la fonction est non nulle) se limite donc
aux éléments du maillage ayant le noeud
(i.e. le lieu des points où la fonction est non nulle) se limite donc
aux éléments du maillage ayant le noeud ![]() pour sommet:
pour sommet:
Ainsi la fonction de base ![]() est non nulle uniquement
sur les éléments
est non nulle uniquement
sur les éléments ![]() et vaut
et vaut
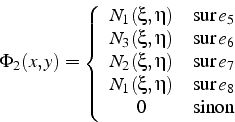
En effet le sommet 2 est le premier sommet sur l'élément ![]() dans la table de connection (6.1), (i.e. Tbc(5,1)=2); le
troisième sur l'élément
dans la table de connection (6.1), (i.e. Tbc(5,1)=2); le
troisième sur l'élément ![]() (i.e. Tbc(6,3)=2), le second sur
l'élément
(i.e. Tbc(6,3)=2), le second sur
l'élément ![]() (i.e. Tbc(7,2)=1), et enfin le premier sur l'élément
(i.e. Tbc(7,2)=1), et enfin le premier sur l'élément
![]() (i.e. Tbc(8,1)=2). Cette fonction de base
(i.e. Tbc(8,1)=2). Cette fonction de base ![]() est tracée en perspective sur la figure (6.7), et sa forme
est une forme pyramidale.
est tracée en perspective sur la figure (6.7), et sa forme
est une forme pyramidale.
La solution approchée ![]() du problème (6.1) est donc
définie à partir de ces
du problème (6.1) est donc
définie à partir de ces ![]() valeurs nodales
valeurs nodales
![]() aux sommets du maillage de la figure (6.2).
aux sommets du maillage de la figure (6.2).
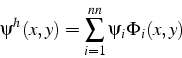
La solution du problème (6.1) doit de plus vérifiée les conditions aux limites fortes, i.e.:
donc la valeur de ![]() est fixé sur les noeuds du maillage
se trouvant sur ces frontières:
est fixé sur les noeuds du maillage
se trouvant sur ces frontières:
Grâce à un choix judicieux de la numérotation des noeuds du maillage,
la solution approchée ![]() s'écrit:
s'écrit:
Après application des conditions aux limites de Dirichlet, le problème discrétisé possède 4 degrés de liberté. En remplaçant la solution exacte par la solution approchée (6.19) dans (6.1) , il vient la formulation faible discrète:
Les fonctions tests ![]() sont déduites de la forme de la solution
approchée (6.19), puisque ce sont des variations
sont déduites de la forme de la solution
approchée (6.19), puisque ce sont des variations
![]() de
de ![]() :
:
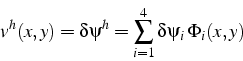
On vérifie que ces fonctions s'annulent sur les frontières de Dirichlet.
Ce sont des combinaisons linéaires des 4 fonctions de base
![]() associées aux 4 degrés de liberté
associées aux 4 degrés de liberté
![]() .
.
En choisissant comme fonctions tests ![]() dans (6.20),
respectivement ces 4 fonctions de base
dans (6.20),
respectivement ces 4 fonctions de base
![]() , on
obtiens les 4 équations qui vont permettre de calculer les 4 inconnues
, on
obtiens les 4 équations qui vont permettre de calculer les 4 inconnues
![]() :
:
![\begin{eqnarray*}
\int_{\Omega}\left[\frac{\partial}{\partial x}\left(\sum_{j=1}...
...ght)\frac{\partial\Phi_{i}}{\partial y}\right]dxdy & =0 & (i=1,4)\end{eqnarray*}](img1225.png)
Après regroupement des termes, en permutant l'intégration et la sommation, les équations s'écrivent:
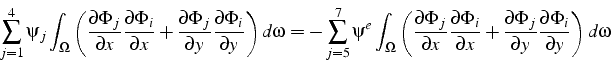
C'est un système linéaire de 4 équations à 4 inconnues, qui s'écrit
sous la forme matricielle:
![]() , où la matrice
, où la matrice
![]() , le second membre
, le second membre ![]() et le vecteur inconnu
et le vecteur inconnu
![]() sont donnés par:
sont donnés par:
![\begin{displaymath}
\mathbf{A}=\left[\begin{array}{cccc}
\int_{\Omega}\overright...
...hi_{4}.\overrightarrow{\nabla}\Phi_{4}d\omega\end{array}\right]\end{displaymath}](img1228.png)
![\begin{displaymath}
\mathbf{B}=-\psi^{e}\left[\begin{array}{c}
\sum_{j=5}^{7}\in...
...hi_{j}.\overrightarrow{\nabla}\Phi_{4}d\omega\end{array}\right]\end{displaymath}](img1230.png)
soit sous forme générique:
On remarque que la matrice ![]() est symétrique due à la symétrie
de la formulation faible.
est symétrique due à la symétrie
de la formulation faible.
La recherche d'une solution approchée par éléments finis dans la formulation
faible se ramène donc à la résolution du système linéaire (6.21).
Il nous reste donc à calculer la matrice ![]() et le second
membre
et le second
membre ![]() . A nouveau, comme dans le chapitre précédent,
nous n'allons pas calculer directement les intégrales dans les relations
(6.22), mais suivre une approche systématique pour le calcul
de
. A nouveau, comme dans le chapitre précédent,
nous n'allons pas calculer directement les intégrales dans les relations
(6.22), mais suivre une approche systématique pour le calcul
de ![]() et
et ![]()
Le calcul des coefficients de ![]() se fait élément par élément,
en notant que l'intégrale sur le domaine
se fait élément par élément,
en notant que l'intégrale sur le domaine ![]() est la somme d'intégrales
élémentaires sur chacun des triangles
est la somme d'intégrales
élémentaires sur chacun des triangles ![]() du maillage:
du maillage:
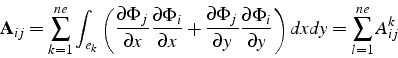
En utilisant la propriété des fonctions de base ![]() qui sont
non nulles uniquement sur le support du noeud i, on constate que les
intégrales élémentaires
qui sont
non nulles uniquement sur le support du noeud i, on constate que les
intégrales élémentaires ![]() sont presque toujours nulles
sauf si l'élément
sont presque toujours nulles
sauf si l'élément ![]() est dans le support du noeud i et du noeud
j, c'est à dire si i et j sont des sommets de l'élément
est dans le support du noeud i et du noeud
j, c'est à dire si i et j sont des sommets de l'élément ![]() .
.
On a donc en réalité ![]() intégrales élémentaires à calculer par
élément
intégrales élémentaires à calculer par
élément ![]() , ce sont, en notant
, ce sont, en notant
![]() les
numéros des 3 sommets de l'élément k:
les
numéros des 3 sommets de l'élément k:
Avec ces notations, le premier coefficient de la matrice ![]() s'écrit
s'écrit
puisque le noeud 1 a pour support les éléments
![]() et correspond au premier sommet sur l'élément
et correspond au premier sommet sur l'élément ![]() , au troisième
sur
, au troisième
sur ![]() , .... De même le second coefficient de
, .... De même le second coefficient de ![]() s'écrit:
s'écrit:
puisque les seuls éléments ayant comme sommet les noeuds 1 et 2 sont
les éléments
![]() . Sur l'élément
. Sur l'élément ![]() le noeud
1 correspond au troisième sommet et le noeud 2 au premier, alors que
sur l'élément
le noeud
1 correspond au troisième sommet et le noeud 2 au premier, alors que
sur l'élément ![]() le noeud 1 correspond au premier sommet et
le noeud 2 au troisième.
le noeud 1 correspond au premier sommet et
le noeud 2 au troisième.
L'assemblage complet de la matrice ![]() donne donc:
donne donc:
Pour calculer les intégrales élémentaires (6.23), on effectue la transformation vers l'élément de référence.
Pour calculer l'intégrale d'une fonction ![]() sur un élément
sur un élément
![]() , on effectue le changement de variable
, on effectue le changement de variable ![]() et
et
![]() pour se ramener à un calcul d'intégrale sur l'élément
de référence. Le calcul de cette intégrale sur l'élément de référence
s'effectue par partie, en intégrant d'abord en
pour se ramener à un calcul d'intégrale sur l'élément
de référence. Le calcul de cette intégrale sur l'élément de référence
s'effectue par partie, en intégrant d'abord en ![]() puis en
puis en ![]() (figure 6.8). On a donc:
(figure 6.8). On a donc:
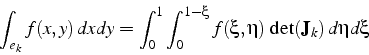
puisque l'on a la relation suivante entre les éléments de surface:
où
![]() est le jacobien (6.14) de la transformation
est le jacobien (6.14) de la transformation
![]() de l'élément de référence
de l'élément de référence ![]() vers l'élément
vers l'élément
![]() vers . En utilisant la relation (6.17) pour le calcul
des dérivées, la matrice élémentaire s'écrit après ce changement de
variable:
vers . En utilisant la relation (6.17) pour le calcul
des dérivées, la matrice élémentaire s'écrit après ce changement de
variable:
En notant que la matrice jacobienne
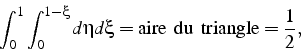
l'intégrale se simplifie:
Un calcul directe du déterminant du Jacobien fournit la valeur:
que l'on peut vérifier en notant que ce déterminant est le rapport
entre l'aire du triangle ![]() :
: ![]() , et l'aire du triangle
de référence
, et l'aire du triangle
de référence ![]() :
: ![]() et. De même par un calcul directe
le produit matriciel
et. De même par un calcul directe
le produit matriciel
![]() s'écrit:
s'écrit:
(
![\begin{displaymath}
(\mathbf{J}_{k}^{-1}).(\mathbf{J}_{k}^{-1})^{t}=\frac{1}{(2a...
...\
(y_{3}^{k}-y_{1}^{k})(y_{1}^{k}-y_{2}^{k})\end{array}\right]\end{displaymath}](img1258.png)
Compte tenu de l'expression (6.12) des fonctions de forme, le calcul de leur gradient est trivial:
![\begin{displaymath}
\overrightarrow{\nabla}N_{1}=\left[\begin{array}{c}
-1\\
-1...
...ow{\nabla}N_{3}=\left[\begin{array}{c}
0\\
1\end{array}\right]\end{displaymath}](img1259.png)
Pour calculer la matrice élémentaire, on peut effectuer le calcul
directe des 9 coefficients à partir de la relation (6.26),
mais on peut aussi remarquer que la matrice élémentaire est symétrique,
et que la somme des lignes (et des colonnes) est nulle (car la somme
des gradients des fonctions de forme est nulle). Il suffit donc de
calculer 3 coefficients:
![]() , les autres étant déduits comme indiqué ci dessous:
, les autres étant déduits comme indiqué ci dessous:
Le calcul de ces 3 coefficients donne
d'où l'expression de la matrice élémentaire
![]() :
:
Exercice: retrouver ce résultat en utilisant l'expression des fonctions d'interpolation dans le plan physique (x,y).
Pour calculer la matrice de notre système, il suffit donc de calculer
les 11 matrices élémentaires correspondants aux ![]() éléments
du maillage en utilisant les relations (6.27) et (6.28),
et de reporter les coefficients dans la matrice globale (6.24).
éléments
du maillage en utilisant les relations (6.27) et (6.28),
et de reporter les coefficients dans la matrice globale (6.24).
On obtiens ainsi les valeurs des coefficients de la matrice du système:
qui est bien entendu symétrique.
Le calcul du second membre (6.22) procède de la même démarche.
On remarque aussi que, dans notre cas, le second membre ne contient
que des termes provenant des conditions aux limites. L'intégrale à
calculer est exactement la même que pour la matrice ![]() ,
et on écrit donc le second membre sous la forme:
,
et on écrit donc le second membre sous la forme:
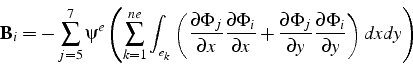
C'est la somme de coefficients de matrices élémentaires
![]() (6.23): pour calculer le second membre
(6.23): pour calculer le second membre
![]() ,
on doit prendre en compte les matrices élémentaires des éléments du
maillage ayant le noeud
,
on doit prendre en compte les matrices élémentaires des éléments du
maillage ayant le noeud ![]() comme sommet et un des noeuds
comme sommet et un des noeuds ![]() sur
le bord
sur
le bord ![]() (i.e.
(i.e. ![]() ). Ainsi pour le second membre
). Ainsi pour le second membre
![]() on a:
on a:
puisque que l'élément ![]() a pour premier sommet le noeud 1 et
pour troisième sommet le noeud 7 (qui sur
a pour premier sommet le noeud 1 et
pour troisième sommet le noeud 7 (qui sur ![]() mais aussi pour
second sommet le noeud 6 (qui sur
mais aussi pour
second sommet le noeud 6 (qui sur ![]() et que l'élément
et que l'élément ![]() a pour troisième sommet le noeud 1 et pour second sommet le noeud
6.
a pour troisième sommet le noeud 1 et pour second sommet le noeud
6.
Le second membre complet s'écrit donc:
![\begin{displaymath}
\mathbf{B}=\left[\begin{array}{c}
-\mathbf{A}_{13}^{4}\psi_{...
...{12}\psi_{e}\\
-\mathbf{A}_{23}^{12}\psi_{e}\end{array}\right]\end{displaymath}](img1276.png)
Le calcul précédent nous a fournit les matrices élémentaires, et on
obtiens comme valeurs de ![]() :
:
compte tenue de la valeur de ![]()
La résolution du système linéaire avec la matrice (6.30) et le second membre (6.31), nous fournit la valeur de la solution approchée pour les 4 degrés de liberté du système:
![\begin{displaymath}
X=\left[\begin{array}{c}
0.2377\\
0.5021\\
0.5010\\
0.5005\end{array}\right]\end{displaymath}](img1279.png)
Compte tenu des conditions aux limites, on obtiens la solution approchée sur tous les noeuds du maillage:
Cette solution est représentée sur la figure (6.9) sous
la forme d'iso-valeurs en couleur. Une ligne ![]() corresponds
à une couleur fixe, dont la valeur est fournit par la palette de couleurs
à droite de la figure. Ces lignes iso-valeurs
corresponds
à une couleur fixe, dont la valeur est fournit par la palette de couleurs
à droite de la figure. Ces lignes iso-valeurs ![]() sont justement
les lignes de courant de l'écoulement . Compte tenu de la petitesse
du maillage, ces lignes de courant approchées ne sont pas très régulières,
mais on retrouve le comportement global de l'écoulement qui est défléchi
par l'obstacle.
sont justement
les lignes de courant de l'écoulement . Compte tenu de la petitesse
du maillage, ces lignes de courant approchées ne sont pas très régulières,
mais on retrouve le comportement global de l'écoulement qui est défléchi
par l'obstacle.
On peut comparer cette solution à la solution calculée sur un maillage beaucoup plus fin de
En comparant les deux figures, on constate que l'allure de l'écoulement
est bien la même, par contre la déviation des lignes de courants sur
le maillage grossier (6.9) est beaucoup trop important en
amont de l'obstacle, comparé à la solution de référence (6.10).
Par contre sur l'obstacle, la solution est quasiment identique et
correspond à une répartition linéaire. Cela est confirmé par la figure
suivante (6.11), où on a tracé les profils de la solution
approchée (en traits pointillés) pour deux abscisses ![]() (droit
de l'obstacle) et
(droit
de l'obstacle) et ![]() (amont de l'obstacle), comparés à la solution
de référence (en traits pleins).
(amont de l'obstacle), comparés à la solution
de référence (en traits pleins).