suivant: 5.3 Étude de la monter: 5. Méthodes des éléments précédent: 5.1 Première approche Table des matières
Après l'étude du paragraphe précédent, nous allons maintenant étudier
l'approximation par éléments finis
![]() d'un problème
générique sur un domaine bidimensionnel
d'un problème
générique sur un domaine bidimensionnel ![]() quelconque (figure
6.12) .
quelconque (figure
6.12) .
La frontière
Chacune de ses frontières correspond à un type de conditions aux limites
appliquées à la solution ![]()
L'équation d'équilibre est une équation de convectionconduction avec
un terme source fonction de la solution. ![]() représente le coefficient
de diffusion
représente le coefficient
de diffusion ![]() ,
, ![]() le coefficient du terme source
le coefficient du terme source ![]() linéaire en
linéaire en ![]() , et
, et ![]() le terme source indépendant de
le terme source indépendant de
![]() .
.
La formulation faible de (6.32) s'obtiens comme toujours
en multipliant par une fonction test ![]() puis en intégrant
sur le domaine
puis en intégrant
sur le domaine ![]() . On intègre ensuite par partie le terme en
dérivée seconde en utilisant la formule de Green. En utilisant les
conditions aux limites et en interprétant la fonction test
. On intègre ensuite par partie le terme en
dérivée seconde en utilisant la formule de Green. En utilisant les
conditions aux limites et en interprétant la fonction test ![]() comme une variation
comme une variation ![]() de la solution
de la solution ![]() , la formulation
faible s'écrit:
, la formulation
faible s'écrit:
Pour calculer la solution approchée ![]() , nous avons besoin d'un
maillage de
, nous avons besoin d'un
maillage de ![]() , et d'une approximation de la solution sur ce
maillage.
, et d'une approximation de la solution sur ce
maillage.
Le domaine de calcul ![]() est découpé en triangles comme sur
la figure (6.13). Ce maillage est construit à l'aide d'outils
informatiques ou de logiciels spécialisés. On trouvera en annexe les
outils de maillage écrit avec Matlab, qui nous ont servi à générer
les différents maillages utilisés dans ce livre.
est découpé en triangles comme sur
la figure (6.13). Ce maillage est construit à l'aide d'outils
informatiques ou de logiciels spécialisés. On trouvera en annexe les
outils de maillage écrit avec Matlab, qui nous ont servi à générer
les différents maillages utilisés dans ce livre.
De façon général, un outil de maillage doit fournir les informations suivantes:
| ligne | champ 1 | champ 2 | champ 3 | champ 4
1 |
Le fichier de maillage de la figure 6.13 contiens par exemple les valeurs suivantes :
30 40 maillage_triangle_P1 0.000000 0.000000 2 0.550000 -0.125000 3 1.100000 -0.250000 3 ................... 0.850000 0.900000 4 1.175000 0.950000 4 1.500000 1.000000 1 1 2 7 1 6 1 7 1 ......... 24 25 30 1 29 24 30 1
Sous Matlab, nous utiliserons une structure de données pour la géométrie de type structure, qui contiendra les champs suivants (en notant G le nom variable géométrie):
function [G]=Lecture(fichier)
% lecture du maillage
% ouverture du fichier
fid=fopen(fichier,'r');
% lecture de la dimension
[L,count]=fscanf(fid,'%d %d %s',3);
G.nn=L(1); G.ne=L(2);
% initialisation structure geometrie
G.dim=2; G.ddl=3;
G.X=zeros(G.nn,G.dim); G.Frt=zeros(G.nn,1);
G.Tbc=zeros(G.ne,G.ddl); G.Reg=zeros(G.ne,1);
% lecture des coordonnees
for i=1:G.nn
[L,count]=fscanf(fid,'%f %f %d',3);
G.X(i,1:2)=[L(1) L(2)];
G.Frt(i)=L(3);
end;
% table deconnection
for l=1:G.ne
[L,count]=fscanf(fid,'%d %d %d %d',4);
G.Tbc(l,1:3)=[L(1) L(2) L(3)];
G.Reg(l)=L(4);
end;
fclose(fid);
return;
Ensuite sous Matlab, pour lire la géométrie stockée dans le fichier maillage.msh, on écrit simplement:
>> G1=Lecture('maillage.msh')
G1 =
nn: 30
ne: 40
dim: 2
ddl: 3
X: [30x2 double]
Frt: [30x1 double]
Tbc: [40x3 double]
Reg: [40x1 double]
On a montré précédemment qu'une approximation ![]() sur un
maillage éléments finis est une combinaison linéaire des valeurs nodales
sur un
maillage éléments finis est une combinaison linéaire des valeurs nodales
![]() sur les noeuds du maillage. les coefficients
de cette combinaison linéaire sont les fonctions de base
sur les noeuds du maillage. les coefficients
de cette combinaison linéaire sont les fonctions de base ![]() :
:

Ces fonctions ![]() forment une base locale, i.e. une fonction
forment une base locale, i.e. une fonction
![]() est non nulle uniquement sur une petite partie du
maillage: le support du noeud
est non nulle uniquement sur une petite partie du
maillage: le support du noeud ![]() , i.e. l'ensemble des éléments
, i.e. l'ensemble des éléments
![]() ayant le noeud
ayant le noeud ![]() comme sommet (
comme sommet (
![]() ).
Elles vérifient en outre les propriétés suivantes:
).
Elles vérifient en outre les propriétés suivantes:

Pour calculer une fonction de base sur un élément ![]() du maillage,
on utilise une transformation (6.10,6.11,6.13)
de cet élément vers un élément de référence
du maillage,
on utilise une transformation (6.10,6.11,6.13)
de cet élément vers un élément de référence ![]() . Sur cet élément
de référence, la fonction de base associée à l'un des sommets
. Sur cet élément
de référence, la fonction de base associée à l'un des sommets
![]() de l'élément
de l'élément ![]() coıncide alors avec l'une des fonctions de forme
coıncide alors avec l'une des fonctions de forme
![]() (6.12) associées aux sommets
(6.12) associées aux sommets
![]() de l'élément de référence
de l'élément de référence ![]() (6.18).
(6.18).
La solution approchée ![]() de l'équation (6.32) s'écrit
sous la forme:
de l'équation (6.32) s'écrit
sous la forme:
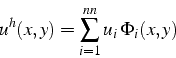
Elle doit de plus vérifier les conditions aux limites de Dirichlet,
i.e.
![]() . Ces conditions
de Dirichlet imposent la valeur nodale de
. Ces conditions
de Dirichlet imposent la valeur nodale de ![]() sur tous les noeuds
se trouvant sur la frontière
sur tous les noeuds
se trouvant sur la frontière ![]() ou
ou ![]() , i.e:
, i.e:
Soit ![]() le nombre de noeuds sur la frontière
le nombre de noeuds sur la frontière ![]() ,
et
,
et ![]() le nombre de noeuds sur la frontière
le nombre de noeuds sur la frontière ![]() , le
nombre de degré de liberté
, le
nombre de degré de liberté ![]() de
de ![]() est égale à
est égale à
![]() .
Cependant la numérotation du maillage étant quelconque, on ne peut
comme dans l'exemple précédent avoir une numérotation simple des degrés
de liberté. En notant
.
Cependant la numérotation du maillage étant quelconque, on ne peut
comme dans l'exemple précédent avoir une numérotation simple des degrés
de liberté. En notant
![]() ,
on écrit la solution sous la forme:
,
on écrit la solution sous la forme:
Les fonctions tests associées ![]() sont des variations de
sont des variations de
![]() , qui doivent donc s'annuller sur les frontières de Dirichlet
, qui doivent donc s'annuller sur les frontières de Dirichlet
![]() et
et ![]() . Elles s'écrivent sous la forme générale
suivante:
. Elles s'écrivent sous la forme générale
suivante:

Ces fonctions tests sont une combinaison linéaire des ![]() fonctions
de base
fonctions
de base ![]() (
(
![]() ). En remplaçant
la solution exacte
). En remplaçant
la solution exacte ![]() par l'expression (6.34) de
par l'expression (6.34) de ![]() et la fonction test
et la fonction test ![]() par une des fonctions de base précédentes
par une des fonctions de base précédentes
![]() , on obtiens la formulation faible discrète:
, on obtiens la formulation faible discrète:
La relation (6.35) écrite pour les ![]() fonctions de base
fonctions de base
![]() appartenant à
appartenant à
![]() , est un système linéaire
de
, est un système linéaire
de ![]() inconnues
inconnues ![]() (
(
![]() ), qu'il
suffit de résoudre pour obtenir la solution approchée
), qu'il
suffit de résoudre pour obtenir la solution approchée ![]() . Le
calcul directe de ce système linéaire nécessiterait une renumérotation
des noeuds, de façon à avoir la même numérotation pour les inconnues
et degrés de liberté (i.e. de 1 à
. Le
calcul directe de ce système linéaire nécessiterait une renumérotation
des noeuds, de façon à avoir la même numérotation pour les inconnues
et degrés de liberté (i.e. de 1 à ![]() pour les noeuds
pour les noeuds
![]() ),
et ce chaque fois que l'on change les conditions aux limites du problème.
De façon à écrire un programme qui soit le plus général possible,
on construira tout d'abord un système linéaire générique pour toutes
les valeurs nodales
),
et ce chaque fois que l'on change les conditions aux limites du problème.
De façon à écrire un programme qui soit le plus général possible,
on construira tout d'abord un système linéaire générique pour toutes
les valeurs nodales
![]() , puis on appliquera les
conditions aux limites du problème sur ce système linéaire de dimension
, puis on appliquera les
conditions aux limites du problème sur ce système linéaire de dimension
![]() .
.
Les coefficients génériques de la matrice ![]() et du second
membre
et du second
membre ![]() s'écrivent:
s'écrivent:

Pour calculer ces coefficients, on effectue un calcul élément par
élément en déterminant les matrices et les second membres élémentaires
sur chaque élément ![]() :
:

En tenant compte des propriétés des fonctions de base, sur un élément
![]() on doit calculer uniquement
on doit calculer uniquement ![]() intégrales élémentaires
faisant intervenir les 3 fonctions de base associées aux 3 sommets
de l'élément. En notant
intégrales élémentaires
faisant intervenir les 3 fonctions de base associées aux 3 sommets
de l'élément. En notant
![]() les numéros de ces
3 sommets, on a donc à calculer sur un élément
les numéros de ces
3 sommets, on a donc à calculer sur un élément ![]() la matrice
élémentaire
la matrice
élémentaire ![]() suivante:
suivante:
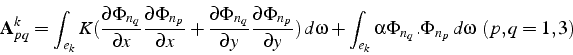
En considérant que les coefficients ![]() et
et ![]() sont constants
sur l'élément
sont constants
sur l'élément ![]() , cette matrice est la somme d'une matrice élémentaire
de rigidité
, cette matrice est la somme d'une matrice élémentaire
de rigidité
![]() et d'une matrice de masse
et d'une matrice de masse
![]() :
:
Le calcul de ces 2 matrices s'effectue à l'aide du changement de variables
vers l'élément de référence ![]() .
.
Nous rappelons l'expression générique (6.25) de la matrice de rigidité calculée sur l'élément de référence:
![\begin{displaymath}
\mathbf{K}_{pq}^{k}=\int_{0}^{1}\left[\int_{0}^{1-\xi}\left(...
...end{array}\right]\right)\det(\mathbf{J}_{k}) d\eta\right]d\xi\end{displaymath}](img1371.png)
Le calcul effectué au paragraphe 6.1.4 montre que cette matrice dépend de 3 coefficients (6.28), que l'on peut écrire sous forme vectorielle:

que l'on reporte dans l'expression de
![]()
![\begin{displaymath}
\mathbf{K}^{k}=\left[\begin{array}{ccc}
K_{22}^{k}+K_{33}^{k...
...{23}^{k}-K_{33}^{k} & K_{23}^{k} & K_{33}^{k}\end{array}\right]\end{displaymath}](img1373.png)
En utilisant les notations matricielles de Matlab, ces formulent se
programment très simplement. La fonction MatriceRigidite
(programme 6.2.4) implémente directement sous Matlab les
relations précédentes. On a aussi utiliser le fait que le produit
vectoriel
![]() a une seule composante non nulle, qui est suivant l'axe
a une seule composante non nulle, qui est suivant l'axe ![]() , et qui
est positive si les sommets sont donnés dans l'ordre trigonométrique
dans la table de connection (ce qui est le cas).
, et qui
est positive si les sommets sont donnés dans l'ordre trigonométrique
dans la table de connection (ce qui est le cas).
function [Ke]=MatriceRigidite(G,k)
% calcul de la matrice de rigidite de l'element k
n=G.Tbc(k,:); % numero des sommets de l'element k
S21=G.X(n(1),:)-G.X(n(2),:);
S13=G.X(n(3),:)-G.X(n(1),:);
Aire=0.5*(S13(1)*S21(2)-S13(2)*S21(1));
K22=S13*S13'/(4*Aire);
K33=S21*S21'/(4*Aire);
K23=(S13*S21')/(4*Aire);
Ke=[K22+K33+2*K23,-K23-K22,-K23-K33;
-K23-K22 , K22 , K23 ;
-K23-K33 , K23 , K33 ];
return;
De manière identique, le changement de variable permet d'obtenir l'expression générique de la matrice de masse:
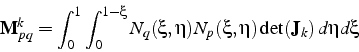
Sur l'élément de référence, le calcul de cette matrice est simple,
puisque le déterminant du jacobien est constant,
![]() et les fonctions de formes
et les fonctions de formes ![]() et
et ![]() sont des polynômes
très simples en (
sont des polynômes
très simples en (![]() ). Compte tenu de l'expression de ces
polynômes (6.12) et des propriétés de symétrie, il suffit
de calculer 2 intégrales:
). Compte tenu de l'expression de ces
polynômes (6.12) et des propriétés de symétrie, il suffit
de calculer 2 intégrales:

En effet les propriétés de symétrie imposent:
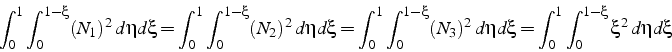

d'où l'expression de la matrice de masse élémentaire:
![\begin{displaymath}
\mathbf{M}^{k}=\frac{aire_{k}}{12}\left[\begin{array}{ccc}
2 & 1 & 1\\
1 & 2 & 1\\
1 & 1 & 2\end{array}\right]\end{displaymath}](img1383.png)
dont la fonction Matlab MatriceMasse est donné (programme
![[*]](crossref.png) ) ci dessous.
) ci dessous.
function [Me]=MatriceMasse(G,k) % calcul de la matrice de rigidite de l'element k n=G.Tbc(k,:); % numero des sommets de l'element k S21=G.X(n(1),:)-G.X(n(2),:); S13=G.X(n(3),:)-G.X(n(1),:); Aire=0.5*(S13(1)*S21(2)-S13(2)*S21(1)); Me=Aire/12*[2,1,1; 1,2,1; 1,1,2]; return;
Pour chaque élément ![]() , on a à calculer 3 intégrales élémentaires
associées à chacun des 3 sommets de l'élément. Avec les mêmes notations
que précédemment, ces intégrales s'écrivent:
, on a à calculer 3 intégrales élémentaires
associées à chacun des 3 sommets de l'élément. Avec les mêmes notations
que précédemment, ces intégrales s'écrivent:

Pour calculer ces intégrales, on remplace la fonction ![]() par
son interpolation
par
son interpolation ![]() sur le maillage éléments finis:
sur le maillage éléments finis:

ce qui permet d'écrire les intégrales sous la forme:
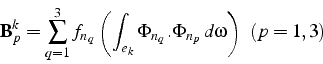
puisque sur l'élément ![]() , l'interpolation
, l'interpolation ![]() de
de ![]() s'écrit:
s'écrit:
![]() .
.
C'est donc le produit du vecteur
![]() des valeurs nodales par la matrice élémentaire de masse
des valeurs nodales par la matrice élémentaire de masse
![]() .
Le second membre élémentaire s'écrit donc:
.
Le second membre élémentaire s'écrit donc:
![\begin{displaymath}
\mathbf{B}^{k}=\mathbf{M}^{k}\mathbf{F}^{k}=\frac{aire_{k}}{...
...array}{c}
f_{n_{1}}\\
f_{n_{2}}\\
f_{n_{3}}\end{array}\right]\end{displaymath}](img1389.png)
et la fonction Matlab SmbElement est donné (programme 6.2.5) ci dessous.
function [Be]=SmbElement(G,F,k) % calcul du second membre elmentaire (F valeurs nodales de f) n=G.Tbc(k,:); % numero des sommets de l'element k Fk=F(n); Mk=MatriceMasse(G,k); Be=Mk*Fk; return;
L'assemblage de la matrice ![]() et du second membre
et du second membre ![]() consiste à passer en revu les éléments, à calculer les matrices élémentaires
de masse et de rigidité ainsi que le second membre élémentaire, puis
à mettre ses valeurs aux bons endroits dans la matrice et le second
membre globale.
consiste à passer en revu les éléments, à calculer les matrices élémentaires
de masse et de rigidité ainsi que le second membre élémentaire, puis
à mettre ses valeurs aux bons endroits dans la matrice et le second
membre globale.
L'algorithme d'assemblage (2) ci dessous donne le principe de l'assemblage.
![\begin{algorithm}
% latex2html id marker 9474\begin{algorithmic}[2]
\STATE $A\...
...mic}\par
\caption{Assemblage de la matrice et du second membre
}
\end{algorithm}](img1390.png)
Le programme Matlab ci dessous implémente cet algorithme, en utilisant
les notations matricielles de Matlab qui permettent d'éviter l'écriture
de boucles. Ainsi les boucles internes 5 à 12 sont remplacées par
2 lignes de codes matriciels Matlab (lignes 11 et 12 dans le programme
6.2.6)
La fonction Matlab Assemblage est donné (programme 6.2.6) ci dessous.
function [A,B]=Assemblage(G,K,alpha,F)
% assemblage de la matrice et du second membre
% K coef. diffusion, alpha coef. source, F terme source
% stocage de A sous forme creuse
% estimation du nbre d'element non nuls nzmax
nzmax=2*G.ddl*G.ne+G.nn;
A=sparse([],[],[],G.nn,G.nn,nzmax);
B=zeros(G.nn,1);
for k=1:G.ne
n=G.Tbc(k,:); % numero des sommets
Ke=MatriceRigidite(G,k);
Me=MatriceMasse(G,k);
Be=SmbElement(G,F,k);
A(n,n)=A(n,n)+K*Ke+alpha*Me;
B(n)=B(n)+Be;
end;
return;
L'application des conditions aux limites sur le système linéaire obtenu après l'assemblage dépend du type de conditions aux limites.
L'imposition des conditions aux limites de Dirichlet (frontières ![]() et
et ![]() ) consiste à fixer la valeur de la solution aux noeuds
) consiste à fixer la valeur de la solution aux noeuds
![]() se trouvant sur la frontière de Dirichlet (
se trouvant sur la frontière de Dirichlet (
![]() ).
Pour cela on remplace simplement dans le système linéaire l'équation
).
Pour cela on remplace simplement dans le système linéaire l'équation
![]() par l'équation:
par l'équation:

Dans la matrice ![]() , cela revient à annuler la ligne
, cela revient à annuler la ligne ![]() et à mettre un 1 sur la diagonale, et dans le second membre
et à mettre un 1 sur la diagonale, et dans le second membre ![]() ,
à remplacer la composante i par 0 ou
,
à remplacer la composante i par 0 ou ![]() selon le cas:
selon le cas:
La condition aux limites de Neuman homogène (frontière ![]() )
est déjà prise en compte dans la formulation et ne nécessite pas de
modification supplémentaire. Par contre la condition mixte sur la
frontière
)
est déjà prise en compte dans la formulation et ne nécessite pas de
modification supplémentaire. Par contre la condition mixte sur la
frontière ![]() nécessite le calcul d'intégrales de bords:
nécessite le calcul d'intégrales de bords:
Compte tenu de la propriété des fonctions de base, ces contributions
interviennent que pour des fonctions de base associées à des noeuds
![]() sur la frontière
sur la frontière ![]() . Le calcul de ces intégrales
se décompose en calcul élémentaire sur les arêtes de la frontière
. Le calcul de ces intégrales
se décompose en calcul élémentaire sur les arêtes de la frontière
![]() . Pour cela nous allons tout d'abord déterminer les arêtes
frontières de la géométrie.
. Pour cela nous allons tout d'abord déterminer les arêtes
frontières de la géométrie.
Soit AF le tableau des arêtes frontières, i.e. l'ensemble
des arêtes des éléments ![]() du maillage se trouvant sur la frontière
du maillage se trouvant sur la frontière
![]() de la géométrie:
de la géométrie:
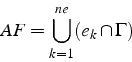
Chaque arête frontière ![]() est définie par le numéro du premier
et du second sommet de l'arête (parcourue dans le sens trigonométrique:
i.e. avec une normale extérieure à droite). Le tableau AF
est donc un tableau de
est définie par le numéro du premier
et du second sommet de l'arête (parcourue dans le sens trigonométrique:
i.e. avec une normale extérieure à droite). Le tableau AF
est donc un tableau de ![]() entiers (en notant
entiers (en notant ![]() le nombre
total d'arêtes frontières). Par exemple pour la maillage de la figure
(6.13), le nombre d'arêtes frontières vaut
le nombre
total d'arêtes frontières). Par exemple pour la maillage de la figure
(6.13), le nombre d'arêtes frontières vaut ![]() , et
le tableau AF vaut:
, et
le tableau AF vaut:
| arêtes AF | numéro 1er sommet | numéro 2nd sommet
1 |
Remarque: l'ordre des arêtes est totalement arbitraire.
Pour déterminer ces arêtes, nous utiliserons l'algorithme (3) suivant:
![\begin{algorithm}
% latex2html id marker 9576\begin{algorithmic}[3]
\par
\STAT...
...{algorithmic}\par
\caption{détermination des arêtes frontières
}
\end{algorithm}](img1401.png)
Il faut noté qu'une arête frontière n'est pas forcément une arête
ayant ses 2 sommets sur la frontière. Ainsi l'élément 33 du maillage
de la figure (6.13) a une arête ![]() dont les deux
sommets sont sur la frontière, mais qui n'est pas frontière. Donc
après avoir déterminé la liste des arêtes ayant les 2 sommets sur
la frontière (lignes 1 à 3), il faut éliminer les arêtes internes,
i.e. apparaissant 2 fois dans la liste. On peut en effet vérifier
la propriété suivante:
dont les deux
sommets sont sur la frontière, mais qui n'est pas frontière. Donc
après avoir déterminé la liste des arêtes ayant les 2 sommets sur
la frontière (lignes 1 à 3), il faut éliminer les arêtes internes,
i.e. apparaissant 2 fois dans la liste. On peut en effet vérifier
la propriété suivante:
![]()
Le programme Matlab 6.2.7 correspondant est donné ci dessous. La fonction Matlab AretesFrt utilise la fonction find de Matlab qui permet de déterminer la liste des indices d'un tableau, dont les valeurs vérifient une condition. Pour tester si un noeud est sur une frontière, on utilise le tableau Frt .
function [AF]=AretesFrt(G)
% determine la liste des aretes frontieres d'un maillage G
% liste des elts frontieres (i.e au moins 1 nds frontiere)
if (G.ddl==3)
Count=G.Frt(G.Tbc(:,1))+G.Frt(G.Tbc(:,2))+G.Frt(G.Tbc(:,3));
Efrt=find(Count>0);
% liste des aretes des elements frontieres
AF0=[G.Tbc(Efrt,1:2); G.Tbc(Efrt,2:3); G.Tbc(Efrt,3), G.Tbc(Efrt,1)] ;
elseif (G.ddl==4)
Count=G.Frt(G.Tbc(:,1))+G.Frt(G.Tbc(:,2))+G.Frt(G.Tbc(:,3))+G.Frt(G.Tbc(:,4));
Efrt=find(Count>0);
% liste des aretes des elements frontieres
AF0=[G.Tbc(Efrt,1:2); G.Tbc(Efrt,2:3); G.Tbc(Efrt,3:4); G.Tbc(Efrt,4), G.Tbc(Efrt,1)] ;
else
disp('Erreur type de geometrie'); return;
end;
% recherche des aretes frontieres parmi cette liste i.e. les 2 nds sur la frontiere
LAF0=find(G.Frt(AF0(:,1))>0 & G.Frt(AF0(:,2))>0) ;
% liste des aretes possiblement frontieres
AF1=AF0(LAF0,:);
% recherche des aretes doubles (non frontiere)
na=size(AF1,1);
for k=1:na-1
ij=AF1(k,:);
% test si arete ji est dans la liste
I=(find(AF1(k+1:na,1)==ij(2) & AF1(k+1:na,2)==ij(1)));
if (~isempty(I)) AF1(k,:)=[0 0]; AF1(k+I,:)=[ 0 0]; end;
end;
% elimination
LAF1=find(AF1(:,1)~=0);
AF=AF1(LAF1,:);
% fin
return;
Ayant la liste AF des arêtes frontières, une intégrale sur
![]() se décompose en intégrale élémentaire:
se décompose en intégrale élémentaire:

Pour calculer les intégrales de bord (6.36), il suffit donc
de calculer des intégrales élémentaires sur les arêtes frontières
de ![]() , soit pour une arête
, soit pour une arête ![]() de sommets
de sommets ![]() et
et ![]() les 6 intégrales suivantes:
les 6 intégrales suivantes:

puisque sur cette arête, seules 2 fonctions de base sont non nulle:
les 2 fonctions de base ![]() et
et ![]() associées
aux 2 sommets. Pour calculer ces intégrales on effectue un changement
de variable de l'arête
associées
aux 2 sommets. Pour calculer ces intégrales on effectue un changement
de variable de l'arête ![]() vers le segment de référence
vers le segment de référence ![]() (figure 6.15).
(figure 6.15).
Sur cet élément, l'expression des 2 fonctions de base est très simple: ce sont les 2 polynômes de Lagrange
puisque ![]() est une fonction affine qui vaut 1 au noeud
est une fonction affine qui vaut 1 au noeud
![]() et 0 au noeud
et 0 au noeud ![]() , et idem pour
, et idem pour ![]() . La
variable
. La
variable ![]() a une interprétation géométrique, puisque c'est l'abscisse
curviligne sur le segment
a une interprétation géométrique, puisque c'est l'abscisse
curviligne sur le segment ![]() .
.
Avec ces notations, les intégrales élémentaires de bord s'écrivent:

en notant ![]() la longueur de l'arête
la longueur de l'arête ![]() . Un calcul élémentaire
fournit la valeur de ces intégrales dans le cas où
. Un calcul élémentaire
fournit la valeur de ces intégrales dans le cas où ![]() et
et ![]() sont constants par arêtes:
sont constants par arêtes:
![\begin{displaymath}
\mathbf{Af}^{l}=\beta h^{l}\left[\begin{array}{cc}
\frac{1}{...
...t[\begin{array}{c}
\frac{1}{2}\\
\frac{1}{2}\end{array}\right]\end{displaymath}](img1418.png)
Le programme Matlab ci dessous implémente cet assemblage. La fonction
Matlab Climite applique les conditions aux limites en modifiant
la matrice et le second membre générique (i.e. calculés sans tenir
compte des conditions aux limites). On utilise aussi la convention
suivante: les arêtes de la frontière ![]() sont les arêtes
ayant au moins un noeud dont le numéro de frontière est égale à 4.
Ainsi pour le maillage de la figure (6.13), la frontière
sont les arêtes
ayant au moins un noeud dont le numéro de frontière est égale à 4.
Ainsi pour le maillage de la figure (6.13), la frontière
![]() va du noeud 30 au noeud 26 (et non de 29 à 27). On calcule
ainsi toutes les intégrales de bords, mais on modifie aussi l'équation
pour les 2 noeuds extrémités 30 et 26. Si ces noeuds sont sur une
frontière de Dirichlet (ce qui est le cas), il faudra imposer la condition
de Dirichlet après le calcul de ces intégrales de bords. C'est ce
qui est fait dans la fonction Matlab Climite
va du noeud 30 au noeud 26 (et non de 29 à 27). On calcule
ainsi toutes les intégrales de bords, mais on modifie aussi l'équation
pour les 2 noeuds extrémités 30 et 26. Si ces noeuds sont sur une
frontière de Dirichlet (ce qui est le cas), il faudra imposer la condition
de Dirichlet après le calcul de ces intégrales de bords. C'est ce
qui est fait dans la fonction Matlab Climite ![[*]](crossref.png) ,
où on impose d'abord les conditions faibles, puis ensuite les conditions
fortes.
,
où on impose d'abord les conditions faibles, puis ensuite les conditions
fortes.
function [A1,B1]=Climite(G,A,B,beta,phi0,Ue)
% application des C.L. sur la matrice A et B
A1=A; B1=B;
% liste des aretes frontieres
AF=AretesFrt(G);
% application des cdts mixtes sur gamam4
AF4=AF(find((G.Frt(AF(:,1))==4)|(G.Frt(AF(:,2))==4)),:);
na=size(AF4,1);
for k=1:na
n1=AF4(k,1); n2=AF4(k,2); % numero des 2 sommets
dx=norm(G.X(n2,:)-G.X(n1,:)); % longueur de l'arete
A1(n1,n1)=A1(n1,n1)+beta*dx/3; A1(n2,n2)=A1(n2,n2)+beta*dx/3;
A1(n1,n2)=A1(n1,n2)+beta*dx/6; A1(n2,n1)=A1(n1,n2)+beta*dx/6;
B1(n1)=B1(n1)-phi0*dx/2;
B1(n2)=B1(n2)-phi0*dx/2;
end;
% applications des cdts fortes
ND1=find(G.Frt(:)==1);
for i=ND1'
A1(i,:)=0; A1(i,i)=1.0; B1(i)=0;
end;
ND2=find(G.Frt(:)==2);
% pour les cdts de Dirichlet on peut passer une fonction
if isa(Ue,'double')
for i=ND2'
A1(i,:)=0; A1(i,i)=1.0; B1(i)=Ue;
end;
else
% Ue est une fonction inline de (x,y)
for i=ND2'
A1(i,:)=0; A1(i,i)=1.0;
B1(i)=Ue(G.X(i,1),G.X(i,2));
end;
end;
return;
Après imposition des conditions aux limites, la solution approchée
![]() s'obtiens par résolution du système linéaire. Le script Matlab
6.2.8 qui enchaıne la suite des opérations pour calculer
cette solution approchée est donné ci-dessous.
s'obtiens par résolution du système linéaire. Le script Matlab
6.2.8 qui enchaıne la suite des opérations pour calculer
cette solution approchée est donné ci-dessous.
% resolution du probleme model
G=Lecture('maillage.msh');
% parametres
alpha=0.; K=1.0; beta=0.0; phi0=-1.0; Ue=2;
% second membre
F=zeros(G.nn,1);
% assemblage
[A,B]=Assemblage(G,K,alpha,F);
% conditions aux limites
[A,B]=Climite(G,A,B,beta,phi0,Ue);
% resolution
% renumerotation pour optimisation
m = symamd(A);
[LA,UA]=lu(A(m,m));
U=UA\(LA\B);
Pour les valeurs des paramètres du programme ci dessus, on a tracé
la solution obtenue pour 2 valeurs de ![]() :
: ![]() et
et
![]() (figure 6.16). On constate, sur ce problème
simple de diffusion sans terme source, l'influence de la condition
aux limites sur
(figure 6.16). On constate, sur ce problème
simple de diffusion sans terme source, l'influence de la condition
aux limites sur ![]() , qui pour le second cas dévie les iso-valeurs
de la solution vers la droite par rapport au cas homogène. Ceci correspond
bien à l'imposition d'une valeur de dérivée normale positive. On note
aussi que les conditions de Neuman ne sont pas vérifiées exactement
par la solution approchée, car les iso-valeurs ne sont pas exactement
perpendiculaires aux frontières de Neuman. C'est seulement à la limite,
que ces conditions seront vérifiées exactement.
, qui pour le second cas dévie les iso-valeurs
de la solution vers la droite par rapport au cas homogène. Ceci correspond
bien à l'imposition d'une valeur de dérivée normale positive. On note
aussi que les conditions de Neuman ne sont pas vérifiées exactement
par la solution approchée, car les iso-valeurs ne sont pas exactement
perpendiculaires aux frontières de Neuman. C'est seulement à la limite,
que ces conditions seront vérifiées exactement.