suivant: 5.4 Éléments finis quadrangulaire monter: 5. Méthodes des éléments précédent: 5.2 Éléments finis triangulaire Table des matières
Pour étudier la précision de l'approximation par éléments finis
![]() ,
nous choisissons un cas d'écoulement potentiel où l'on connaıt la
solution analytique: l'écoulement autour d'un cylindre.
,
nous choisissons un cas d'écoulement potentiel où l'on connaıt la
solution analytique: l'écoulement autour d'un cylindre.
Soit un cylindre de rayon ![]() , placé dans un écoulement uniforme
de vitesse
, placé dans un écoulement uniforme
de vitesse ![]() suivant x. L'écoulement potentiel autour du cylindre
est donnée par la fonction de courant
suivant x. L'écoulement potentiel autour du cylindre
est donnée par la fonction de courant ![]() en coordonnées
polaires
en coordonnées
polaires ![]() :
:
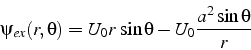
qui vérifie l'équation de Laplace:
et la condition aux limites de glissement sur le cylindre:
Considérons le domaine ![]() de la figure (6.17) de
frontière ABCD (soit 1/4 du domaine complet). Sur ce domaine les conditions
aux limites sont:
de la figure (6.17) de
frontière ABCD (soit 1/4 du domaine complet). Sur ce domaine les conditions
aux limites sont:
Pour générer le maillage du domaine ![]() , nous utiliserons les
programmes Matlab de génération de maillage décrits en annexe. Plus
précisément, nous utiliserons la fonction quacou qui maille
un domaine à l'aide d'une transformation “quadrilatères
courbes” des frontières vers un carré unité que l'on maille (figure
6.18).
, nous utiliserons les
programmes Matlab de génération de maillage décrits en annexe. Plus
précisément, nous utiliserons la fonction quacou qui maille
un domaine à l'aide d'une transformation “quadrilatères
courbes” des frontières vers un carré unité que l'on maille (figure
6.18).
On spécifie les points des cotés AB, BC , CD et DA en notant que le nombre de noeuds sur les faces opposées doivent être égaux. Le listing 6.3.1 ci dessous donne la fonction Matlab cylindremesh utilisée pour le maillage de
function [G]=cylindremesh(n1,n2) % maillage du cylindre addpath ../Mailleur % construction de la geometrie R1=1; R2=3; A=[-R2,0]; B=[-R1,0]; C=[0,R1]; D=[0,R2]; AB=[linspace(A(1),B(1),n1)',linspace(A(2),B(2),n1)']; theta=linspace(pi,pi/2,n2)'; BC=[R1*cos(theta),R1*sin(theta)]; CD=[linspace(C(1),D(1),n1)',linspace(C(2),D(2),n1)']; theta=linspace(pi/2,pi,n2)'; DA=[R2*cos(theta),R2*sin(theta)]; G=Quacou(AB,BC,CD,DA,[1,1,3,2]); return;
Le maillage obtenu pour ![]() et
et ![]() est tracé sur la
figure 6.19. Ce maillage comprend 400 noeuds et 722 éléments.
est tracé sur la
figure 6.19. Ce maillage comprend 400 noeuds et 722 éléments.
En utilisant les programmes précédents, on construit la matrice A
et le second membre B du problème discrétisé par éléments
finis. Avec l'approche utilisée, la matrice ![]() est une matrice
est une matrice ![]() qui contient
qui contient ![]() éléments dans le cas du maillage de la figure
(6.19). Or la matrice A a une structure creuse,
c'est à dire qu'il y a très peu d'éléments non nuls. Dans notre cas
A possède uniquement
éléments dans le cas du maillage de la figure
(6.19). Or la matrice A a une structure creuse,
c'est à dire qu'il y a très peu d'éléments non nuls. Dans notre cas
A possède uniquement ![]() éléments non nuls, soit moins
de
éléments non nuls, soit moins
de ![]() .
.
Exercice: montrer qu'en moyenne pour des éléments
![]() ,
le nombre d'éléments non nuls de A est
,
le nombre d'éléments non nuls de A est ![]()
Au lieu de stocker la matrice A sous la forme d'un tableau à 2 indices, on utilise un stockage creux (sparse en anglais) pour lequel on ne conserve que les éléments non nuls. Pour cela on ne stocke que les valeurs
![\begin{displaymath}
\mathbf{M}=\left[\begin{array}{cccc}
2.0 & 0 & 0 & -1.0\\
0...
...& 0\\
0 & -3.0 & 1.0 & 0\\
0 & 0 & 0 & -2.0\end{array}\right]\end{displaymath}](img1451.png)
le stockage creux de cette matrice correspond au tableau de 6 lignes et 3 colonnes suivant:
| i | j
2.0 |
Dans le cas de la matrice A précédente ce stockage creux
est très efficace puisque que l'on utilise un tableau de ![]() éléments au lieu d'un tableau de
éléments au lieu d'un tableau de ![]() éléments. Par contre
si la matrice A est une matrice creuse, son inverse
éléments. Par contre
si la matrice A est une matrice creuse, son inverse
![]() est en général une matrice pleine comme le montre la figure 6.20,
où on a marqué par un point bleu les éléments non nuls de A
et de
est en général une matrice pleine comme le montre la figure 6.20,
où on a marqué par un point bleu les éléments non nuls de A
et de
![]() . Pour la résolution d'un système linéaire
linéaire avec une matrice creuse, il faut donc utiliser des méthodes
numériques adaptées. Nous avons choisi d'utiliser une factorisation
LU de la matrice A qui préserve au maximum le caractère
creux de la matrice. Comme le montre la figure 6.20, cette
factorisation génère
. Pour la résolution d'un système linéaire
linéaire avec une matrice creuse, il faut donc utiliser des méthodes
numériques adaptées. Nous avons choisi d'utiliser une factorisation
LU de la matrice A qui préserve au maximum le caractère
creux de la matrice. Comme le montre la figure 6.20, cette
factorisation génère ![]() éléments non nuls au lieu des
éléments non nuls au lieu des ![]() de
de
![]() (soit
(soit ![]() ). Cette factorisation est relativement
efficace puisque que la numérotation des noeuds est telle que les
éléments non nuls sont proches de la diagonale (voir figure 6.20)
. Dans le cas d'une numérotation quelconque, il faut appliquer une
renumérotation des noeuds de façon à minimiser le remplissage de la
matrice lors de la factorisation (par un algorithme de Cuthill-McKee
ou un algorithme de degré minimum, tous les deux implémenter sous
Matlab par les fonctions colrcm et colamd).
). Cette factorisation est relativement
efficace puisque que la numérotation des noeuds est telle que les
éléments non nuls sont proches de la diagonale (voir figure 6.20)
. Dans le cas d'une numérotation quelconque, il faut appliquer une
renumérotation des noeuds de façon à minimiser le remplissage de la
matrice lors de la factorisation (par un algorithme de Cuthill-McKee
ou un algorithme de degré minimum, tous les deux implémenter sous
Matlab par les fonctions colrcm et colamd).
On peut encore améliorer le stockage en tenant compte du caractère
symétrique de la matrice A et en ne stockant que la partie
triangulaire supérieure de A. Dans ce cas, il faut symétriser
la prise en compte des conditions aux limites de Dirichlet: pour un
noeud i tel que
![]() , il modifier la ligne i et la
colonne i de A ainsi que le second membre B:
, il modifier la ligne i et la
colonne i de A ainsi que le second membre B:
![\begin{eqnarray*}
\mathbf{B}\leftarrow\mathbf{B}-\psi^{e}[A_{i,k}]_{k=1,nn} & B_{1}=\psi^{e}\\
A_{i,k}=A_{k,i}=0 & (k=1,nn)\\
A_{i,i=1}\end{eqnarray*}](img1459.png)
Exercice: modifier les programmes Matlab pour prendre en compte cette symétrie.
Pour utiliser un stockage “matrice creuse”, nous avons modifier le programme Matlab d'assemblage en déclarant la matrice A sparse (ligne 7 dans le programme 6.3.2 ci dessous).
function [A,B]=Assemblage(G,K,alpha,F)
% assemblage de la matrice et du second membre
% K coef. diffusion, alpha coef. source, F terme source
% stocage de A sous forme creuse
% estimation du nbre d'element non nuls nzmax
nzmax=2*G.ddl*G.ne+G.nn;
A=sparse([],[],[],G.nn,G.nn,nzmax);
B=zeros(G.nn,1);
for k=1:G.ne
n=G.Tbc(k,:); % numero des sommets
Ke=MatriceRigidite(G,k);
Me=MatriceMasse(G,k);
Be=SmbElement(G,F,k);
A(n,n)=A(n,n)+K*Ke+alpha*Me;
B(n)=B(n)+Be;
end;
return;
Pour cela on fournit une estimation du nombre d'éléments non nuls de A à partir d'un nombre d'arêtes par élément (ligne 6).
Exercice: montrez que le coefficient ![]() est
non nul si
est
non nul si ![]() est une arête du maillage.
est une arête du maillage.
Sur chaque élément on a 3 cotés donc 6 arêtes , soit au total une
estimation de ![]() arêtes et donc
arêtes et donc ![]() éléments non nuls. Cette
estimation est grossière puisque l'on compte deux fois les arêtes
internes. Une estimation exacte nécessiterait de déterminer les arêtes
de la géométrie. Dans notre cas le calcul exacte donne
éléments non nuls. Cette
estimation est grossière puisque l'on compte deux fois les arêtes
internes. Une estimation exacte nécessiterait de déterminer les arêtes
de la géométrie. Dans notre cas le calcul exacte donne ![]() arêtes
pour une estimation de
arêtes
pour une estimation de ![]() soit un nombre d'éléments non nuls
estimé de
soit un nombre d'éléments non nuls
estimé de ![]() pour
pour ![]() .
.
Exercice: écrire l'algorithme et le programme Matlab permettant de déterminer les arêtes de la géométrie.
C'est la seule modification apportée au programme d'assemblage, puisque les calculs des matrices et second membres élémentaires sont inchangés.
Avec ces modifications, la solution approchée ![]() s'obtiens
par résolution du système linéaire par factorisation LU. Le script
Matlab
s'obtiens
par résolution du système linéaire par factorisation LU. Le script
Matlab ![[*]](crossref.png) qui enchaıne la suite des opérations pour calculer
cette solution approchée est donné ci-dessous.
qui enchaıne la suite des opérations pour calculer
cette solution approchée est donné ci-dessous.
% maillage du cylindre
G=cylindremesh(20,20);
% second membre
F=zeros(G.nn,1);
% assemblage
[A,B]=Assemblage(G,1.0,0.0,F);
% conditions aux limites
Psie=inline('y-y./(x.^2+y.^2)','x','y');
[A,B]=Climite(G,A,B,0.0,0.0,Psie);
% resolution
[LA,UA]=lu(A);
Psi=UA\(LA\B);
% calcul de l'erreur
err=Erreur(G,Psie,Psi)
Le solution obtenue est tracé sur la figure (6.21).
Pour déterminer la précision de cette solution numérique ![]() ,
il faut calculer la norme de l'erreur entre la solution exacte
,
il faut calculer la norme de l'erreur entre la solution exacte ![]() et la solution approchée
et la solution approchée ![]() :
:
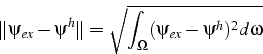
Le calcul de l'intégrale se fait par assemblage, avec un calcul élément par élément:
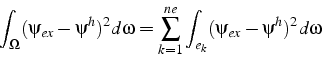
et chaque intégrale élémentaire est calculé par transformation sur l'élément de référence:
La fonction ![]() n'étant pas polynômiale, on ne sait pas calculer
analytiquement cette intégrale. On choisit une intégration numérique
par points de Gauss. On approxime l' intégrale d'une fonction
n'étant pas polynômiale, on ne sait pas calculer
analytiquement cette intégrale. On choisit une intégration numérique
par points de Gauss. On approxime l' intégrale d'une fonction ![]() sur le triangle de référence par une formule de quadrature de Gauss:
i.e par une somme pondérée (de poids
sur le triangle de référence par une formule de quadrature de Gauss:
i.e par une somme pondérée (de poids ![]() de valeurs de
de valeurs de ![]() en
en ![]() points de Gauss de coordonnées
points de Gauss de coordonnées
![]() :
:
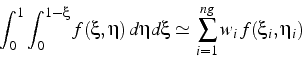
Les poids ![]() et les coordonnées
et les coordonnées
![]() des points
de Gauss sont tels que la formule de quadrature soit exacte pour des
polynômes de degré le plus élevé possible. Cette formule possède
des points
de Gauss sont tels que la formule de quadrature soit exacte pour des
polynômes de degré le plus élevé possible. Cette formule possède ![]() degrés de liberté, on peux donc imposer
degrés de liberté, on peux donc imposer ![]() contraintes. Ainsi
pour intégrer exactement des polynômes de degré 1 en
contraintes. Ainsi
pour intégrer exactement des polynômes de degré 1 en ![]() (ce qui impose 3 conditions) , il suffit d'un seul point de Gauss,
l'intersection des médianes:
(ce qui impose 3 conditions) , il suffit d'un seul point de Gauss,
l'intersection des médianes:
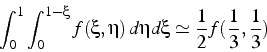
Exercice: démontrer cette formule de quadrature.
Pour un triangle, les points de Gauss doivent vérifier des propriétés de symétrie: i.e. leurs coordonnées barycentriques sont obtenues par permutations circulaires et les poids sont équivalents. Les points de Gauss sont donc à une même distance sur les médianes du triangle.
Ainsi la formule de quadrature utilisant 3 points de Gauss sur les médianes s'écrit:
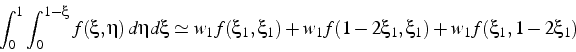
En écrivant que cette formule doit être exacte pour les polynômes
de degré ![]() , i.e. pour
, i.e. pour
![]() ,
on en déduit les relations (non linéaires) que doivent vérifier
,
on en déduit les relations (non linéaires) que doivent vérifier ![]() et
et ![]() .Parmi ces relations, deux sont indépendantes, ce qui
permet de déterminer
.Parmi ces relations, deux sont indépendantes, ce qui
permet de déterminer ![]() et
et ![]() .
.
Le programme Maple 6.3.3 ci-dessous détermine ces relations et résout le problème non-linéaire. Dans ce cas on trouve 2 solutions:
qui permette d'intégrer exactement des polynômes de degré ![]() .
La seconde solution est la plus précise, puisque l'erreur d'intégration
pour des polynômes de degré 3 est la plus faible.
.
La seconde solution est la plus précise, puisque l'erreur d'intégration
pour des polynômes de degré 3 est la plus faible.
> restart: # Formule de quadrature sur un triangle avec 3 pts > F:='F':Ie:=int(int(F(chi,eta),eta=0..1-chi),chi=0..1); > F:='F':Ih:=w1*F(xi1,eta1)+w2*F(xi2,eta2)+w3*F(xi3,eta3); # Cdts de symetrie > w2:=w1; w3:=w1; eta1:=xi1; xi2:=1-2*xi1; eta2:=xi1; xi3:=xi1; > eta3:=1-2*xi1; > Ih; # 6 conditions > F:=(xi,eta)->1;eval(Ih-Ie=0);rel1:=%: > w1:=solve(rel1,w1); > F:=(xi,eta)->xi;eval(Ih-Ie=0);rel2:=%: > F:=(xi,eta)->eta;eval(Ih-Ie=0);rel3:=%: > F:=(xi,eta)->xi*eta;expand(eval(Ih-Ie=0));rel4:=%: > F:=(xi,eta)->xi^2;expand(eval(Ih-Ie=0));rel5:=%: > F:=(xi,eta)->eta^2;expand(eval(Ih-Ie=0));rel6:=%: # Une seule relation indépendante: 2 solutions > solve(rel6,xi1); > xi1:=1/2; F:='F': Ih; > F:=(xi,eta)->xi^3;eval(Ih-Ie=0); > xi1:=1/6; F:='F': Ih; > F:=(xi,eta)->xi^3;eval(Ih-Ie=0);
Avec cette approche, on peut déterminer les points de Gauss pour des intégrations exactes de polynômes. Dans le tableau (6.2) sont donnés les formules de quadrature de Gauss précises de l'ordre 1 à 5. Les paramètres exactes de ces formules de Gauss, obtenus avec Maple en suivant la même démarche que précédemment, sont donnés dans le tableau (6.3), ainsi que leurs valeurs numériques approchées5.3..
|
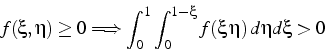
Cette formule n'est donc pas utilisable en pratique et seul les ordres
2,4 ou 5 sont utilisés.
|
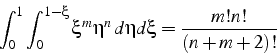
d'où l'on déduit la formule d'intégration pour les fonctions de forme:
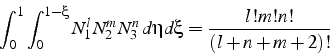
Exercice: démontrer cette formule (à l'aide de Maple).
Pour calculer l'intégrale élémentaire dans l'expression de l'erreur (6.38), nous avons utilisé une intégration numérique d'ordre 2 avec 3 points de Gauss. La fonction Matlab Erreur 6.3.3 correspondante qui calcul l'erreur globale (6.38),est donnée ci dessous.
function [err]=Erreur(G,f,F)
% calcul de l'erreur en norme L2
% pts de Gauss
Xsi=[1.0/6.0,2.0/3.0,1.0/6.0];
Eta=[1.0/6.0,1.0/6.0,2.0/3.0];
P=[1-Xsi-Eta;Xsi;Eta];
err=0.0;
for k=1:G.ne
% calcul de l'erreur / elt
n=G.Tbc(k,:); % numero des sommets de l'element k
S21=G.X(n(1),:)-G.X(n(2),:);
S13=G.X(n(3),:)-G.X(n(1),:);
Aire=0.5*(S13(1)*S21(2)-S13(2)*S21(1));
% calcul des coordonnees des pts de Gauss
X=P*G.X(n,:);
% erreur sur l'elt k
errk=(f(X(:,1),X(:,2))-P*F(n));
err=err+errk'*errk*Aire/3;
end;
err=sqrt(err);
return;
La précision d'une solution par éléments finis dépend du degré de
l'élément et de la taille ![]() des éléments. Pour un triangle
des éléments. Pour un triangle ![]() ,
on définit la taille
,
on définit la taille ![]() comme la longueur du plus grand coté
(figure6.22 ). On définit aussi le diamètre
comme la longueur du plus grand coté
(figure6.22 ). On définit aussi le diamètre ![]() du
cercle inscrit et le diamètre
du
cercle inscrit et le diamètre ![]() du cercle circonscrit, ainsi
que le rapport d'aspect du triangle
du cercle circonscrit, ainsi
que le rapport d'aspect du triangle
![]() . Pour
un triangle équilatéral, on a
. Pour
un triangle équilatéral, on a ![]() et
et
![]() ,
donc
,
donc
![]() . Par contre pour un triangle de plus
en plus aplati, le rapport d'aspect tend vers 0 (car
. Par contre pour un triangle de plus
en plus aplati, le rapport d'aspect tend vers 0 (car
![]() )
, ce qui indique la dégénérescence du triangle.
)
, ce qui indique la dégénérescence du triangle.
Avec ces définitions, on montre que l'erreur d'interpolation
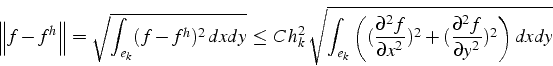
Cependant la constante ![]() dépend du rapport d'aspect
dépend du rapport d'aspect ![]() et l'estimation
d'erreur dégénère lorsque
et l'estimation
d'erreur dégénère lorsque ![]() , i.e. lorsque le triangle
devient de plus en plus aplatis.
, i.e. lorsque le triangle
devient de plus en plus aplatis.
L'erreur d'approximation étant borné par l'erreur d'interpolation,
on déduit une estimation de l'erreur d'approximation
![]() sur un maillage non dégénéré de taille caractéristique
sur un maillage non dégénéré de taille caractéristique ![]() :
:
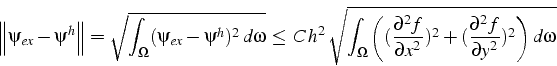
Nous avons donc construit une série de maillage de ![]() avec
une taille
avec
une taille ![]() et un rapport d'aspect
et un rapport d'aspect ![]() constant en
fixant un nombre de noeuds identiques sur les cotés lors de la génération
du maillage: i.e.
constant en
fixant un nombre de noeuds identiques sur les cotés lors de la génération
du maillage: i.e. ![]() . Dans ce cas la taille des éléments
. Dans ce cas la taille des éléments
![]() est proportionnelle à
est proportionnelle à ![]() . On a donc tracé sur la
figure 6.23, la norme de l'erreur en fonction de
. On a donc tracé sur la
figure 6.23, la norme de l'erreur en fonction de ![]() et
on vérifie que l'on obtiens une décroissance de l'erreur en
et
on vérifie que l'on obtiens une décroissance de l'erreur en ![]() ,
soit en
,
soit en ![]() , ce qui montre que l'approximation par éléments
finis
, ce qui montre que l'approximation par éléments
finis
![]() est d'ordre 2.
est d'ordre 2.