suivant: 6. Problème hyperbolique: modes monter: 5. Méthodes des éléments précédent: 5.3 Étude de la Table des matières
La seconde façon de mailler un domaine ![]() est d'utiliser des
quadrangles. Bien qu'ayant des possibilités de maillage moins générale
que les triangles, les maillages quadrangulaires sont cependant très
utilisés, en particulier en mécanique des solides, car ils peuvent
être plus précis. L'autre intérêt des approximations quadrangulaires
est que ce sont des produits tensoriels d'approximation 1D.
est d'utiliser des
quadrangles. Bien qu'ayant des possibilités de maillage moins générale
que les triangles, les maillages quadrangulaires sont cependant très
utilisés, en particulier en mécanique des solides, car ils peuvent
être plus précis. L'autre intérêt des approximations quadrangulaires
est que ce sont des produits tensoriels d'approximation 1D.
Le maillage quadrangulaire est décrit par une structure de données G identique à celle du maillage triangulaire du paragraphe 6.3.1, mais avec G.ddl=4 et une table de connection G.Tbc à 4 éléments ( de dimension 4*ne). Un exemple de maillage du cylindre est donné sur la figure 6.24.
L'élément
![]() est l'élément quadrangulaire le plus
simple, qui possède comme degrés de liberté les valeurs aux 4 sommets
du quadrangle.
est l'élément quadrangulaire le plus
simple, qui possède comme degrés de liberté les valeurs aux 4 sommets
du quadrangle.
L'approximation sur un élément
![]() est définie à l'aide
d'une transformation vers un élément de référence, qui est le carré
est définie à l'aide
d'une transformation vers un élément de référence, qui est le carré
![]() .
.
Cette transformation
Sur cet élément de référence, l'approximation ![]() d'une fonction
d'une fonction
![]() est une fonction bilinéaire (i.e. le produit d'un polynôme de
degré 1 en
est une fonction bilinéaire (i.e. le produit d'un polynôme de
degré 1 en ![]() par un polynôme de degré 1 en
par un polynôme de degré 1 en ![]() ):
):
Les coefficients ![]() dépendent linéairement des valeurs
dépendent linéairement des valeurs
![]() de
de ![]() aux 4 sommets de l'élément (on
a noté
aux 4 sommets de l'élément (on
a noté
![]() les numéros des 4 sommets). Cette approximation
s'écrit donc sous la forme:
les numéros des 4 sommets). Cette approximation
s'écrit donc sous la forme:
| (5.39) |
Les fonctions
![]() sont les fonctions de
forme de l'élément
sont les fonctions de
forme de l'élément
![]() : ce sont des fonctions bilinéaires
qui vérifient:
: ce sont des fonctions bilinéaires
qui vérifient:
Ce sont les polynômes de Lagrange de degré 1, dont l'expression est la suivante:
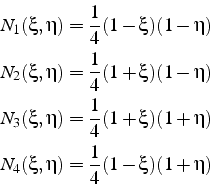
Ces fonctions de forme
![]() sont tracées sur la figure
6.26. Ce sont des surfaces réglées et non plus des plans
comme pour les fonctions de forme
sont tracées sur la figure
6.26. Ce sont des surfaces réglées et non plus des plans
comme pour les fonctions de forme
![]() .
.
Ces fonctions de formes vont nous permettre aussi de déterminer la transformation
| (5.40) | |||
La matrice jacobienne
![]() =
=
![]() de cette transformation se calcule alors simplement:
de cette transformation se calcule alors simplement:
![\begin{displaymath}
\mathbf{J}_{k}=\frac{1}{4}\left[\begin{array}{cc}
(x_{n_{2}}...
..._{n_{1}})(1-\xi)+(y_{n_{3}}-y_{n_{2}})(1+\xi)\end{array}\right]\end{displaymath}](img1597.png) |
(5.41) |
On constate que contrairement à l'élément
![]() , la matrice
jacobienne de cette transformation n'est pas constante. Dans le cas
d'un quadrangle rectangle de cotés
, la matrice
jacobienne de cette transformation n'est pas constante. Dans le cas
d'un quadrangle rectangle de cotés ![]() et
et ![]() alignés avec
les axes, cette matrice jacobienne
alignés avec
les axes, cette matrice jacobienne
![]() se simplifie:
se simplifie:
![\begin{displaymath}
\mathbf{J}_{k}=\frac{1}{2}\left[\begin{array}{cc}
h_{1} & 0\\
0 & h_{2}\end{array}\right]\end{displaymath}](img1600.png)
Exercice: montrer que si les cotés du quadrangles sont
parallèles, alors la matrice jacobienne est constante. Calculer
![]() dans ce cas.
dans ce cas.
Le programme Matlab JacobienQ1 ![[*]](crossref.png) ci dessous
calcule la matrice Jacobienne en un point
ci dessous
calcule la matrice Jacobienne en un point ![]() d'un élément
d'un élément
![]() .
.
function [J]=JacobienQ1(G,k,xi,eta)
% calcul le jacobien de l'elt k au pt xi,eta
n=G.Tbc(k,:); % numero des nds
X=G.X(n,1);
Y=G.X(n,2);
J= 1/4*[(X(2)-X(1))*(1-eta)+(X(3)-X(4))*(1+eta),...
(X(4)-X(1))*(1-xi)+ (X(3)-X(2))*(1+xi);...
(Y(2)-Y(1))*(1-eta)+(Y(3)-Y(4))*(1+eta),...
(Y(4)-Y(1))*(1-xi)+ (Y(3)-Y(2))*(1+xi)];
return;
La transformation vers l'élément de référence est pour un quadrangle
quelconque plus complexe que pour les éléments
![]() .
Le calcul des intégrales sur l'élément de référence, qui fait intervenir
le déterminant du Jacobien, voir la jacobienne inverse, ne se fait
plus en générale analytiquement, mais utilise une intégration numérique.
.
Le calcul des intégrales sur l'élément de référence, qui fait intervenir
le déterminant du Jacobien, voir la jacobienne inverse, ne se fait
plus en générale analytiquement, mais utilise une intégration numérique.
L'intégration numérique sur l'élément de référence
![]() est cependant plus simple que l'intégration numérique sur un élément
est cependant plus simple que l'intégration numérique sur un élément
![]() , puisque les bornes d'intégration en
, puisque les bornes d'intégration en ![]() sont fixes. Cette intégration est en faite un produit tensoriel d'intégrations
numériques en 1D.
sont fixes. Cette intégration est en faite un produit tensoriel d'intégrations
numériques en 1D.
Sur le segment de référence ![]() , l'intégration numérique d'une
fonction
, l'intégration numérique d'une
fonction ![]() utilisant
utilisant ![]() points de Gauss s'écrit:
points de Gauss s'écrit:

Les paramètres de cette formule de quadrature sont tels que l'intégration
soit exacte pour les polynômes de degré le plus élevé possible. Cette
formule ayant ![]() paramètres
paramètres
![]() , on va pouvoir
imposer
, on va pouvoir
imposer ![]() conditions: i.e intégrer exactement tous les monômes
conditions: i.e intégrer exactement tous les monômes
![]() pour
pour ![]() . La formule d'intégration avec
. La formule d'intégration avec ![]() points de Gauss va permettre d'intégrer exactement tous les polynômes
de degré
points de Gauss va permettre d'intégrer exactement tous les polynômes
de degré ![]() .
.
Par exemple avec 2 points de Gauss on peut intégré exactement des
polynômes de degré ![]() . Cette formule s'écrit:
. Cette formule s'écrit:
En écrivant que cette formule (6.42) est exacte pour
![]() on obtiens les 4 relations permettant de déterminer les 4 coefficients
on obtiens les 4 relations permettant de déterminer les 4 coefficients
![]() . On peut aussi noter que cette
formule doit être symétrique, et donc que l'on a forcément:
. On peut aussi noter que cette
formule doit être symétrique, et donc que l'on a forcément:
![]() et
et ![]() . La condition pour
. La condition pour ![]() donne immédiatement la
valeur
donne immédiatement la
valeur ![]() , et la condition pour
, et la condition pour ![]() la valeur
la valeur
![]() .
D'où la formule de quadrature à 2 points:
.
D'où la formule de quadrature à 2 points:
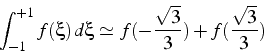
Les positions ![]() des points de Gauss sont les racines de polynômes
caractéristiques: les polynômes de Legendre.On a cependant pas d'expressions
analytiques générales pour ces racines, et il faut les déterminer
pour chaque valeur de
des points de Gauss sont les racines de polynômes
caractéristiques: les polynômes de Legendre.On a cependant pas d'expressions
analytiques générales pour ces racines, et il faut les déterminer
pour chaque valeur de ![]() .
.
A l'aide de Maple, on a déterminer analytiquement ces valeurs jusqu'à
![]() en utilisant les propriétés de symétrie de ces points de Gauss.
Le programme Maple 6.4.2 ci dessous détermine la formule
de quadrature de Gauss pour
en utilisant les propriétés de symétrie de ces points de Gauss.
Le programme Maple 6.4.2 ci dessous détermine la formule
de quadrature de Gauss pour ![]()
> restart: # Formule de Gauss en 1D 3pts > f:='f': > Ie:=int(f(xi),xi=-1..1);Ih:=w1*f(xi1)+w2*f(xi2)+w3*f(xi3); # Conditions de symetrie > w2:=w1; xi2:=-xi1; xi3:=0; Ih; # 6 conditions > f:=xi->1; Ie=Ih; eq1:=%: > w3:=solve(eq1,w3); > f:=xi->xi; Ie=Ih; eq1:=%: > f:=xi->xi^2; Ie=Ih; eq1:=%: > w1:=solve(eq1,w1); > f:=xi->xi^3; Ie=Ih; > f:=xi->xi^4; Ie=Ih;eq1:=%: > solve(eq1,xi1); > xi1:=sqrt(3/5); > f:=xi->xi^5; Ie=Ih; > f:='f':Ih;
Exercice: en s'inspirant du programme précédent, déterminer
la formule de quadrature de Gauss pour ![]()
Le tableau 6.4 donne les expressions analytiques, ainsi
que les valeurs numériques approchées (que l'on comparera avec les
valeurs numériques données classiquement dans les livres), pour les
formules de quadrature de Gauss d'ordre 1 à 9 (i.e. pour ![]() ).
).
Ayant les formules de quadrature de Gauss en 1D, on en déduit les
formules de quadrature en 2D en intégrant successivement suivant ![]() et
et ![]() :
:
Cette formule de quadrature (6.43) est bien le produit tensoriel de formule 1D.
Remarque: on peut évidement choisir un nombre de points de Gauss différent suivant chaque direction.
Par rapport à la formulation élément finis
![]() , le
seul changement provient du calcul des matrices élémentaires, puisque
l'assemblage et le calcul des intégrales de bords restent identiques.
, le
seul changement provient du calcul des matrices élémentaires, puisque
l'assemblage et le calcul des intégrales de bords restent identiques.
L'expression de la matrice élémentaire de rigidité
![]() s'écrit:
s'écrit:
![\begin{displaymath}
\mathbf{K}_{pq}^{k}=\int_{-1}^{+1}\int_{-1}^{+1}\left(\left[...
...y}\right]\right)\det(\mathbf{J}_{k}) d\eta d\xi p,q=1,4\end{displaymath}](img1667.png)
Pour calculer ces intégrales, nous utiliserons une intégration numérique
avec 2 points de Gauss dans chaque direction. La fonction Matlab MatriceRigiditeQ1
6.4.3 implémente le calcul de la matrice de rigidité pour
un élément ![]() quelconque.
quelconque.
function [Ke]=MatriceRigiditeQ1(G,k)
% calcul de la matrice de masse de l'element k (Q1)
% gradient des fonction de forme
dN1=inline('[-(1-eta)/4,-(1-xi)/4]','xi','eta');
dN2=inline('[ (1-eta)/4,-(1+xi)/4]','xi','eta');
dN3=inline('[ (1+eta)/4, (1+xi)/4]','xi','eta');
dN4=inline('[-(1+eta)/4, (1-xi)/4]','xi','eta');
% pts de Gauss 2pts
Xg=[-sqrt(3)/3,sqrt(3)/3];
Wg=[1,1];
ng=size(Wg,2);
% integration numerique
Ke=zeros(4,4);
for i=1:ng
for j=1:ng
J=JacobienQ1(G,k,Xg(i),Xg(j));
J1=inv(J);
detJ=det(J);
dN=[dN1(Xg(i),Xg(j)); dN2(Xg(i),Xg(j)); ...
dN3(Xg(i),Xg(j)); dN4(Xg(i),Xg(j))];
% gradient dans l'espace physique
dP=dN(:,:)*J1;
Ke=Ke+Wg(i)*Wg(j)*det(J)*(dP(:,1)*dP(:,1)'+dP(:,2)*dP(:,2)');
end;
end;
return;
Remarque: on peut vérifier numériquement que la précision d'intégration est suffisante, puisque que pour des quadrangles pas trop déformés, on obtiens la solution exacte.
Dans le cas d'un triangle rectangle de cotés ![]() et
et ![]() alignés suivant les axes
alignés suivant les axes ![]() et
et ![]() , la matrice jacobienne est constante
et on peut calculer analytiquement la matrice de rigidité:
, la matrice jacobienne est constante
et on peut calculer analytiquement la matrice de rigidité:
![\begin{displaymath}
\mathbf{K}^{k}=\frac{1}{6h_{1}h_{2}}\left[\begin{array}{cccc...
...h_{1}^{2}-2h_{2}^{2} & 2(h_{1}^{2}+h_{2}^{2})\end{array}\right]\end{displaymath}](img1669.png)
On vérifie que la matrice est symétrique et que la somme des lignes et des colonnes est nulle.
Exercice: démontrer la relation précédente pour
![]()
L'expression de la matrice élémentaire de masse
![]() s'écrit:
s'écrit:

Pour calculer ces intégrales nous utiliserons une intégration numérique
de Gauss avec 2 points de Gauss dans chaque direction, bien que l'on
puisse les calculer analytiquement. En effet le déterminant du Jacobien
![]() est un polynôme de degré 1 en
est un polynôme de degré 1 en ![]() et
et ![]() et donc
et donc
![]() est une intégrale de polynômes de degré
3 en
est une intégrale de polynômes de degré
3 en ![]() et
et ![]() . Mais l'expression obtenue reste cependant
complexe et n'est pas généralisable au cas où le coefficient
. Mais l'expression obtenue reste cependant
complexe et n'est pas généralisable au cas où le coefficient ![]() devant la matrice de masse est variable.
devant la matrice de masse est variable.
La fonction Matlab MatriceMasseQ1 6.4.3 implémente
le calcul de la matrice de masse pour un élément ![]() quelconque.
quelconque.
function [Me]=MatriceMasseQ1(G,k)
% calcul de la matrice de masse de l'element k (Q1)
% fonction de forme
N1=inline('(1-xi)/2*(1-eta)/2','xi','eta');
N2=inline('(1+xi)/2*(1-eta)/2','xi','eta');
N3=inline('(1+xi)/2*(1+eta)/2','xi','eta');
N4=inline('(1-xi)/2*(1+eta)/2','xi','eta');
% pts de Gauss 2pts
Xg=[-sqrt(3)/3,sqrt(3)/3];
Wg=[1,1];
%
ng=size(Wg,2);
% integration numerique
Me=zeros(4,4);
for i=1:ng
for j=1:ng
J=JacobienQ1(G,k,Xg(i),Xg(j));
detJ=det(J);
N=[N1(Xg(i),Xg(j)),N2(Xg(i),Xg(j)),N3(Xg(i),Xg(j)),N4(Xg(i),Xg(j))];
Me=Me+Wg(i)*Wg(j)*det(J)*N'*N;
end;
end;
return;
Dans le cas d'un triangle rectangle de cotés ![]() et
et ![]() alignés suivant les axes
alignés suivant les axes ![]() et
et ![]() , le Jacobien de la transformation
est constant et on peut calculer simplement la matrice de masse:
, le Jacobien de la transformation
est constant et on peut calculer simplement la matrice de masse:
![\begin{displaymath}
\mathbf{M}_{pq}^{k}=\frac{h_{1}h_{2}}{36}\left[\begin{array}...
...& 4 & 2 & 1\\
1 & 2 & 4 & 2\\
2 & 1 & 2 & 4\end{array}\right]\end{displaymath}](img1674.png)
Exercice: montrer que l'on obtiens la même expression de la matrice de masse pour un rectangle non aligné avec les axes.
Comme dans le cas
![]() , le second membre élémentaire
s'écrit comme le produit de la matrice de masse par le vecteur
, le second membre élémentaire
s'écrit comme le produit de la matrice de masse par le vecteur ![]() élémentaire des valeurs nodales de
élémentaire des valeurs nodales de ![]() :
:
La fonction Matlab SmbElementQ1 6.4.3 est alors une simple adaptation de la fonction SmbElement
function [Be]=SmbElementQ1(G,F,k) % calcul du second membre elmentaire (F valeurs nodales de f) n=G.Tbc(k,:); % numero des sommets de l'element k Fk=F(n); Mk=MatriceMasseQ1(G,k); Be=Mk*Fk; return;
Nous allons étudier le même cas qu'au paragraphe 6.3, mais
avec des éléments
![]() . Le maillage est obtenu par transformation
“quadrilatère courbe” et utilise les programmes Matlab
de maillage décrit en annexe.
. Le maillage est obtenu par transformation
“quadrilatère courbe” et utilise les programmes Matlab
de maillage décrit en annexe.
Le programme 6.4.4 ci dessous donne la fonction Matlab cylindremeshQ1
utilisée pour le maillage de ![]() , paramétré par le nombre de
noeuds
, paramétré par le nombre de
noeuds ![]() et
et ![]() sur les cotés AB et BC.
sur les cotés AB et BC.
function G=cylindremeshQ1(n1,n2) % maillage du cylindre en Q1 addpath ../Mailleur % construction de la geometrie R1=1; R2=3; A=[-R2,0]; B=[-R1,0]; C=[0,R1]; D=[0,R2]; AB=[linspace(A(1),B(1),n1)',linspace(A(2),B(2),n1)']; theta=linspace(pi,pi/2,n2)'; BC=[R1*cos(theta),R1*sin(theta)]; CD=[linspace(C(1),D(1),n1)',linspace(C(2),D(2),n1)']; theta=linspace(pi/2,pi,n2)'; DA=[R2*cos(theta),R2*sin(theta)]; G=Quacou(AB,BC,CD,DA,[1,1,3,2],2); return;
Le script Matlab 6.4.4 qui enchaıne la suite des opérations
pour calculer la solution approchée du problème (6.37) avec
des éléments
![]() est donné ci-dessous.
est donné ci-dessous.
% maillage du cylindre en Q1
G=cylindremeshQ1(20,20);
% second membre
F=zeros(G.nn,1);
% assemblage
[A,B]=AssemblageQ1(G,1.0,0.0,F);
% conditions aux limites
Psie=inline('y-y./(x.^2+y.^2)','x','y');
[A,B]=Climite(G,A,B,0.0,0.0,Psie);
% resolution
[LA,UA]=lu(A);
Psi=UA\(LA\B);
% calcul de l'erreur
err=ErreurQ1(G,Psie,Psi)
Le calcul a été effectué sur un maillage ayant le même nombre de noeuds
(
![]() ) que celui utilisé au paragraphe 6.3.2pour
les éléments
) que celui utilisé au paragraphe 6.3.2pour
les éléments
![]() . La solution obtenue est tracée sur
la figure (), que l'on peut comparer avec la solution
. La solution obtenue est tracée sur
la figure (), que l'on peut comparer avec la solution
![]() sur un maillage équivalent (figure 6.21). On constate que
les deux solutions sont quasiment identiques (le maillage étant relativement
fin pour ce type de calcul).
sur un maillage équivalent (figure 6.21). On constate que
les deux solutions sont quasiment identiques (le maillage étant relativement
fin pour ce type de calcul).
Pour étudier la précision, nous avons fait varier la taille caractéristique
![]() des éléments du maillage et nous avons calculer l'erreur d'approximation
des éléments du maillage et nous avons calculer l'erreur d'approximation
![]() . Comme en
. Comme en
![]() ,
nous avons calculer l'erreur élémentaire sur un élément à l'aide d'une
intégration numérique utilisant 3 points de Gauss dans chaque direction.
,
nous avons calculer l'erreur élémentaire sur un élément à l'aide d'une
intégration numérique utilisant 3 points de Gauss dans chaque direction.
Remarque: pour le calcul de l'erreur nous avons utilisé
plus de points de Gauss ![]() que pour la calcul de la solution
approchée (
que pour la calcul de la solution
approchée (![]() , de façon à minimiser l'erreur numérique d'intégration
par rapport à l'erreur d'approximation.
, de façon à minimiser l'erreur numérique d'intégration
par rapport à l'erreur d'approximation.
La fonction Matlab ErreurQ1 (programme 6.4.4) correspondante qui calcul l'erreur globale (6.38),est donnée ci dessous.
function [err]=ErreurQ1(G,f,F)
% calcul de l'erreur en norme L2
% pts de Gauss
% pts de Gauss 3pts
Xg=[-sqrt(15)/5,0,sqrt(15)/5];
Wg=[5/9,8/9,5/9];
ng=size(Wg,2);
% fct de forme
N1=inline('(1-xi)/2*(1-eta)/2','xi','eta');
N2=inline('(1+xi)/2*(1-eta)/2','xi','eta');
N3=inline('(1+xi)/2*(1+eta)/2','xi','eta');
N4=inline('(1-xi)/2*(1+eta)/2','xi','eta');
err=0.0;
for k=1:G.ne
% calcul de l'erreur / elt
n=G.Tbc(k,:); % numero des sommets de l'element k
for i=1:ng
for j=1:ng
J=JacobienQ1(G,k,Xg(i),Xg(j));
detJ=det(J);
% calcul des coordonnees des pts de Gauss
N=[N1(Xg(i),Xg(j)),N2(Xg(i),Xg(j)),...
N3(Xg(i),Xg(j)),N4(Xg(i),Xg(j))];
X=N*G.X(n,:);
% erreur sur l'elt k
errk=(f(X(:,1),X(:,2))-N*F(n));
err=err+Wg(i)*Wg(j)*detJ*errk^2;
end;
end;
end;
err=sqrt(err);
return;
Nous avons donc construit une série de maillage de ![]() avec
une taille
avec
une taille ![]() et un rapport d'aspect
et un rapport d'aspect ![]() constant en
fixant un nombre de noeuds identiques sur les cotés lors de la génération
du maillage: i.e.
constant en
fixant un nombre de noeuds identiques sur les cotés lors de la génération
du maillage: i.e. ![]() . Dans ce cas la taille des éléments
. Dans ce cas la taille des éléments
![]() est proportionnelle à
est proportionnelle à ![]() . On a donc tracé sur la
figure 6.28, la norme de l'erreur en fonction de
. On a donc tracé sur la
figure 6.28, la norme de l'erreur en fonction de ![]() et
on vérifie que l'on obtiens une décroissance de l'erreur en
et
on vérifie que l'on obtiens une décroissance de l'erreur en ![]() ,
soit en
,
soit en ![]() , ce qui montre que l'approximation par éléments
finis
, ce qui montre que l'approximation par éléments
finis
![]() est d'ordre 2. En comparant la courbe obtenue
avec celle de la figure 6.23, on constate que dans ce cas
l'erreur est un peu plus faible avec les éléments
est d'ordre 2. En comparant la courbe obtenue
avec celle de la figure 6.23, on constate que dans ce cas
l'erreur est un peu plus faible avec les éléments
![]() qu'avec les éléments
qu'avec les éléments
![]() . C'est une constatation assez
générale dans le cas de solutions régulières alignées avec le maillage.
. C'est une constatation assez
générale dans le cas de solutions régulières alignées avec le maillage.