suivant: 6.4 Assemblage et calcul monter: 6. Problème hyperbolique: modes précédent: 6.2 Formulation faible Table des matières
Pour construire une approximation ![]() par éléments finis de la
solution de (7.6), on utilise un maillage
par éléments finis de la
solution de (7.6), on utilise un maillage
![]() du domaine de calcul
du domaine de calcul ![]() en
en ![]() éléments
éléments
![]() associé à
associé à ![]() noeuds
noeuds
![]() . On choisit
ensuite une interpolation en espace de la solution. Pour notre étude
nous utiliserons des éléments finis
. On choisit
ensuite une interpolation en espace de la solution. Pour notre étude
nous utiliserons des éléments finis
![]() . La solution
approchée s'écrit alors comme une combinaison linéaire des fonctions
de base
. La solution
approchée s'écrit alors comme une combinaison linéaire des fonctions
de base
![]() associées à ce maillage
associées à ce maillage
![]() et à l'interpolation
et à l'interpolation
![]() :
:
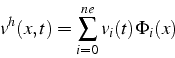
En tenant compte des conditions aux limites (7.5), et
des propriétés des fonctions de base
![]() :
:
l'approximation possède ![]() degrés de liberté et s'écrit:
degrés de liberté et s'écrit:
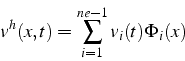
On note que, contrairement aux problèmes statiques étudiés précédemment,
les coefficients ![]() de la combinaison linéaire (valeurs nodales)
dépendent maintenant du temps. Les fonctions tests
de la combinaison linéaire (valeurs nodales)
dépendent maintenant du temps. Les fonctions tests ![]() étant
des variations (à
étant
des variations (à ![]() fixé) de la solution
fixé) de la solution ![]() , c.a.d. une combinaison
des fonctions de base, on choisit comme fonctions tests les fonctions
de base
, c.a.d. une combinaison
des fonctions de base, on choisit comme fonctions tests les fonctions
de base ![]() . La formulation faible discréte s'écrit alors:
. La formulation faible discréte s'écrit alors:
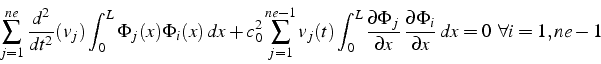
C'est un système de ![]() équations différentielles linéaires du
second ordre qui s'écrit sous la forme matricielle:
équations différentielles linéaires du
second ordre qui s'écrit sous la forme matricielle:
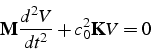
où ![]() est la matrice de masse,
est la matrice de masse, ![]() la matrice
de rigidité et
la matrice
de rigidité et ![]() le vecteur inconnu des valeurs nodales:
le vecteur inconnu des valeurs nodales:
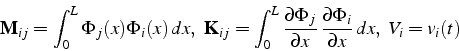
Ce système s'écrit sous la forme suivante (noté le signe - devant
la matrice ![]() ):
):
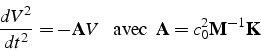
auquel on ajoute les conditions initiales (7.6). La matrice
![]() est une matrice symétrique et définie positive6.2, puisque
est une matrice symétrique et définie positive6.2, puisque ![]() et
et ![]() sont des matrices symétriques
définies positives.
sont des matrices symétriques
définies positives. ![]() possède donc
possède donc ![]() valeurs propres
réelles positives, que l'on note
valeurs propres
réelles positives, que l'on note
![]() .
.
La solution générale de ce système d'équations différentielles linéaires
est donc la somme de ![]() solutions élémentaires où modes propres
solutions élémentaires où modes propres
![]() :
:
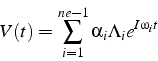
les ![]() étant les vecteurs propres associés aux valeurs
propres
étant les vecteurs propres associés aux valeurs
propres
![]() de la matrice
de la matrice ![]() :
:
D'un point de vue mécanique, la vibration du système est une combinaison
de modes propres de vibration ![]() associés à des fréquences
propres
associés à des fréquences
propres
![]() . On obtiens ainsi les premiers
modes de vibrations de la corde.
. On obtiens ainsi les premiers
modes de vibrations de la corde.